6.5: Dividir monomios
- Page ID
- 110359
Al final de esta sección, podrás:
- Simplificar expresiones usando la propiedad de cociente para exponentes
- Simplifique expresiones con cero exponentes
- Simplificar expresiones usando el cociente a una propiedad de potencia
- Simplificar expresiones aplicando varias propiedades
- Dividir monomios
Antes de comenzar, toma este cuestionario de preparación.
- Simplificar:\(\dfrac{8}{24}\).
Si te perdiste este problema, revisa el Ejercicio 1.6.4. - Simplificar:\((2m^3)^5\).
Si te perdiste este problema, revisa el Ejercicio 6.2.22. - Simplificar:\(\dfrac{12x}{12y}\)
Si te perdiste este problema, revisa Ejercicio 1.6.10.
Simplificar expresiones mediante la propiedad de cociente para exponentes
Anteriormente en este capítulo, desarrollamos las propiedades de los exponentes para la multiplicación. Resumimos estas propiedades a continuación.
Si a y b son números reales, y m y n son números enteros, entonces
\[\begin{array}{ll}{\textbf { Product Property }} & {a^{m} \cdot a^{n}=a^{m+n}} \\ {\textbf { Power Property }} & {\left(a^{m}\right)^{n}=a^{m n}} \\ {\textbf { Product to a Power }} & {(a b)^{m}=a^{m} b^{m}}\end{array}\]
Ahora veremos las propiedades exponentes para la división. Un rápido repaso de la memoria puede ayudar antes de comenzar. Has aprendido a simplificar fracciones dividiendo los factores comunes del numerador y denominador usando la Propiedad de Fracciones Equivalentes. Esta propiedad también le ayudará a trabajar con fracciones algebraicas, que también son cocientes.
Si a, b, y c son números enteros donde\(b\neq 0,c\neq 0\).
\[\text{then} \quad \dfrac{a}{b}=\dfrac{a \cdot c}{b \cdot c} \quad \text{and} \quad \dfrac{a \cdot c}{b \cdot c}=\dfrac{a}{b}\]
Como antes, intentaremos descubrir una propiedad mirando algunos ejemplos.
\[\begin{array}{lclc}{\text { Consider }} & \dfrac{x^{5}}{x^{2}} & \text{and} & \dfrac{x^{2}}{x^{3}}\\ {\text { What do they mean? }}&\dfrac{x \cdot x \cdot x \cdot x \cdot x}{x \cdot x} && \dfrac{x \cdot x}{x \cdot x \cdot x}\\ {\text { Use the Equivalent Fractions Property. }} & {\dfrac{x \not\cdot x \not\cdot x \cdot x \cdot x}{x \not\cdot\not x}} && \dfrac{\not x \cdot\not x \cdot 1}{x \not \cdot\not x \cdot x}\\ {\text { Simplify. }} & {x^{3}} & & \dfrac{1}{x}\end{array}\]
Observe, en cada caso las bases fueron las mismas y restamos exponentes.
Cuando el exponente mayor estaba en el numerador, nos quedamos con factores en el numerador.
Cuando el exponente mayor estaba en el denominador, nos quedamos con factores en el denominador—observe el numerador de 1.
Escribimos:
\[\begin{array}{cc}{\dfrac{x^{5}}{x^{2}}} & {\dfrac{x^{2}}{x^{3}}} \\ {x^{5-2}} & {\dfrac{1}{x^{3-2}}} \\ {x^{3}} & {\dfrac{1}{x}}\end{array}\]
Esto lleva a la Propiedad de Cociente para Exponentes.
Si a es un número real\(a\neq 0\), y m y n son números enteros, entonces
\[\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \text { and } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}, n>m\]
Un par de ejemplos con números pueden ayudar a verificar esta propiedad.
\[\begin{array} {llllll} \dfrac{3^{4}}{3^{2}} &=&3^{4-2}& \dfrac{5^{2}}{5^{3}} &=&\dfrac{1}{5^{3-2}} \\ \dfrac{81}{9} &=&3^{2} & \dfrac{25}{125} &=&\dfrac{1}{5^{1}} \\ 9 &=&9\checkmark& \dfrac{1}{5} &=&\dfrac{1}{5} \checkmark \end{array}\]
Simplificar:
- \(\dfrac{x^{9}}{x^{7}}\)
- \(\dfrac{3^{10}}{3^{2}}\)
- Contestar
-
Para simplificar una expresión con un cociente, primero necesitamos comparar los exponentes en el numerador y denominador.
1.
Desde 9 > 7, hay más factores de x en el numerador.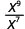 
Utilizar la Propiedad Cociente,\(\dfrac{a^{m}}{a^{n}}=a^{m-n}\)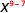 
Simplificar. \(x^2\) 2.
Observe que cuando el exponente mayor está en el numerador, nos quedan factores en el numerador.Desde 10 > 2, hay más factores de x en el numerador.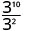 
Utilizar la Propiedad Cociente,\(\dfrac{a^{m}}{a^{n}}=a^{m-n}\) 
Simplificar. \(3^8\)
Simplificar:
- \(\dfrac{x^{15}}{x^{10}}\)
- \(\dfrac{6^{14}}{6^{5}}\)
- Contestar
-
- \(x^{5}\)
- \(6^9\)
Simplificar:
- \(\dfrac{y^{43}}{y^{37}}\)
- \(\dfrac{10^{15}}{10^{7}}\)
- Contestar
-
- \(y^{6}\)
- \(10^8\)
Simplificar:
- \(\dfrac{b^{8}}{b^{12}}\)
- \(\dfrac{7^{3}}{7^{5}}\)
- Contestar
-
Para simplificar una expresión con un cociente, primero necesitamos comparar los exponentes en el numerador y denominador.
1.
Desde 12 > 8, hay más factores de b en el denominador.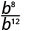 
Utilizar la Propiedad Cociente,\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\)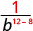 
Simplificar.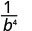 
2.
Observe que cuando el exponente mayor está en el denominador, nos quedan factores en el denominador.Desde 5 > 3, hay más factores de 3 en el denominador.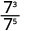 
Utilizar la Propiedad Cociente,\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\)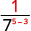 
Simplificar.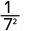 
Simplificar.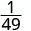 
Simplificar:
- \(\dfrac{x^{18}}{x^{22}}\)
- \(\dfrac{12^{15}}{12^{30}}\)
- Contestar
-
- \(\dfrac{1}{x^{4}}\)
- \(\dfrac{1}{12^{15}}\)
Simplificar:
- \(\dfrac{m^{7}}{m^{15}}\)
- \(\dfrac{9^{8}}{9^{19}}\)
- Contestar
-
- \(\dfrac{1}{m^{8}}\)
- \(\dfrac{1}{9^{11}}\)
Observe la diferencia en los dos ejemplos anteriores:
- Si empezamos con más factores en el numerador, terminaremos con factores en el numerador.
- Si empezamos con más factores en el denominador, terminaremos con factores en el denominador.
El primer paso para simplificar una expresión usando la propiedad de cociente para exponentes es determinar si el exponente es mayor en el numerador o en el denominador.
Simplificar:
- \(\dfrac{a^{5}}{a^{9}}\)
- \(\dfrac{x^{11}}{x^{7}}\)
- Contestar
-
1. ¿Es el exponente de un mayor en el numerador o denominador? Desde 9 > 5, hay más a's en el denominador y así terminaremos con factores en el denominador.
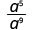
Utilizar la Propiedad Cociente,\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\)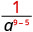 
Simplificar.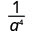 
2. Observe que hay más factores de xx en el numerador, ya que 11 > 7. Entonces terminaremos con factores en el numerador.
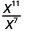
Utilizar la Propiedad Cociente,\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\)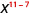 
Simplificar.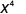 
Simplificar:
- \(\dfrac{b^{19}}{b^{11}}\)
- \(\dfrac{z^{5}}{z^{11}}\)
- Contestar
-
- \(b^{8}\)
- \(\dfrac{1}{z^{6}}\)
Simplificar:
- \(\dfrac{p^{9}}{p^{17}}\)
- \(\dfrac{w^{13}}{w^{9}}\)
- Contestar
-
- \(\dfrac{1}{p^{8}}\)
- \(w^{4}\)
Simplifique las expresiones con un exponente de cero
Un caso especial de la Propiedad Cociente es cuando los exponentes del numerador y denominador son iguales, como una expresión como\(\dfrac{a^{m}}{a^{m}}\). De tu trabajo anterior con fracciones, sabes que:
\[\dfrac{2}{2}=1 \quad \dfrac{17}{17}=1 \quad \dfrac{-43}{-43}=1\]
En palabras, un número dividido por sí mismo es 1. Entonces,\(\dfrac{x}{x}=1\), para cualquiera\(x(x\neq 0)\), ya que cualquier número dividido por sí mismo es 1.
La propiedad de cociente para exponentes nos muestra cómo simplificar\(\dfrac{a^{m}}{a^{n}}\) cuándo\(m>n\) y cuándo\(n<m\) restando exponentes. ¿Y si\(m=n\)?
Consideremos\(\dfrac{8}{8}\), lo que sabemos es 1.
\(\begin{array} {lrll} & \dfrac{8}{8} &=&1 \\ \text { Write } 8 \text { as } 2^{3} . & \dfrac{2^{3}}{2^{3}} &=&1 \\ \text { Subtract exponents. } & 2^{3-3} &=&1 \\ \text { Simplify. } & 2^{0} &=&1 \end{array}\)
Ahora vamos a simplificar\(\dfrac{a^{m}}{a^{m}}\) de dos maneras para llevarnos a la definición del exponente cero. En general, para\(a\neq 0\):
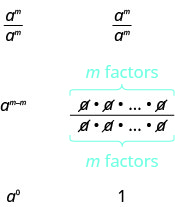
Vemos\(\dfrac{a^{m}}{a^{m}}\) simplifica a\(a^{0}\) y a 1. Entonces\(a^{0} = 1\).
Si a es un número distinto de cero, entonces\(a^{0} = 1\).
Cualquier número distinto de cero elevado a la potencia cero es 1.
En este texto, asumimos que cualquier variable que elevemos a la potencia cero no es cero.
Simplificar:
- \(9^{0}\)
- \(n^{0}\)
- Contestar
-
La definición dice que cualquier número distinto de cero elevado a la potencia cero es 1.
- \(\begin{array}{ll} & 9^0\\ \text{Use the definition of the zero exponent.} & 1 \end{array}\)
- \(\begin{array}{ll} & n^0\\ \text{Use the definition of the zero exponent.} & 1 \end{array}\)
Simplificar:
- \(15^{0}\)
- \(m^{0}\)
- Contestar
-
- 1
- 1
Simplificar:
- \(k^{0}\)
- \(29^{0}\)
- Contestar
-
- 1
- 1
Ahora que hemos definido el exponente cero, podemos expandir todas las Propiedades de los Exponentes para incluir exponentes de número entero.
¿Qué pasa con elevar una expresión a la potencia cero? Echemos un vistazo\((2x)^0\). Podemos usar el producto a una regla de poder para reescribir esta expresión.
\[\begin{array}{ll} & (2x)^0\\ {\text { Use the product to a power rule. }} & {2^{0} x^{0}} \\ {\text { Use the zero exponent property. }} & {1 \cdot 1} \\ {\text { Simplify. }} & 1\end{array}\]
Esto nos dice que cualquier expresión distinta de cero elevada a la potencia cero es una.
Simplificar:
- \((5b)^0\)
- \((−4a^{2}b)^0\).
- Contestar
-
- \(\begin{array}{ll} & (5b)^0\\ {\text {Use the definition of the zero exponent.}} & 1\end{array}\)
- \(\begin{array}{ll} & (−4a^{2}b)^0\\ {\text {Use the definition of the zero exponent.}} & 1\end{array}\)
Simplificar:
- \((11z)^0\)
- \((−11pq^{3})^0\).
- Contestar
-
- 1
- 1
Simplificar:
- \((-6d)^0\)
- \((−8m^{2}n^{3})^0\).
- Contestar
-
- 1
- 1
Simplificar expresiones usando el cociente a una propiedad de potencia
Ahora veremos un ejemplo que nos llevará al Cociente a una Propiedad de Poder.
\[\begin{array}{lc} & {\left(\dfrac{x}{y}\right)^{3}} \\ \text{This means:} & {\dfrac{x}{y} \cdot \dfrac{x}{y} \cdot \dfrac{x}{y}} \\ \text{Multiply the fractions.} &{\dfrac{x \cdot x \cdot x}{y \cdot y \cdot y}} \\ \text{Write with exponents.} & {\dfrac{x^{3}}{y^{3}}}\end{array}\]
Observe que el exponente aplica tanto al numerador como al denominador.
\[\begin{array}{lc}{\text { We see that }\left(\dfrac{x}{y}\right)^{3} \text { is } \dfrac{x^{3}}{y^{3}}} \\ {\text { We write: }} & \left(\dfrac{x}{y}\right)^{3} \\ & {\dfrac{x^{3}}{y^{3}}} \end{array}\]
Esto lleva al Cociente a una Propiedad de Poder para los Exponentes.
Si a y b son números reales\(b\neq 0\), y m es un número de conteo, entonces
\[\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\]
Para elevar una fracción a una potencia, elevar el numerador y denominador a ese poder.
Un ejemplo con números puede ayudarle a entender esta propiedad:
\[\begin{aligned}\left(\dfrac{2}{3}\right)^{3} &=\dfrac{2^{3}}{3^{3}} \\ \dfrac{2}{3} \cdot \dfrac{2}{3} \cdot \dfrac{2}{3} &=\dfrac{8}{27} \\ \dfrac{8}{27} &=\dfrac{8}{27}\checkmark \end{aligned}\]
Simplificar:
- \(\left(\dfrac{3}{7}\right)^{2}\)
- \(\left(\dfrac{b}{3}\right)^{4}\)
- \(\left(\dfrac{k}{j}\right)^{3}\)
- Contestar
-
1.
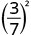
Utilizar la Propiedad Cociente,\(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\)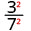 
Simplificar.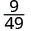 
2.
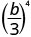
Utilizar la Propiedad Cociente,\(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\)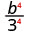 
Simplificar.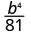 
3.
Elevar el numerador y el denominador a la tercera potencia.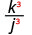 
Simplificar:
- \(\left(\dfrac{5}{8}\right)^{2}\)
- \(\left(\dfrac{p}{10}\right)^{4}\)
- \(\left(\dfrac{m}{n}\right)^{7}\)
- Contestar
-
- \(\dfrac{25}{64}\)
- \(\dfrac{p^{4}}{10,000}\)
- \(\dfrac{m^{7}}{n^{7}}\)
Simplificar:
- \(\left(\dfrac{1}{3}\right)^{3}\)
- \(\left(\dfrac{-2}{q}\right)^{3}\)
- \(\left(\dfrac{w}{x}\right)^{4}\)
- Contestar
-
- \(\dfrac{1}{27}\)
- \(\dfrac{-8}{q^{3}}\)
- \(\dfrac{w^{4}}{x^{4}}\)
Simplificar expresiones mediante la aplicación de varias propiedades
Ahora vamos a resumir todas las propiedades de los exponentes para que estén todos juntos para referirse a medida que simplificamos las expresiones usando varias propiedades. Observe que ahora están definidos para exponentes de número entero.
Si a y b son números reales, y m y n son números enteros, entonces
\[\begin{array}{lrll} \textbf{Product Property} & a^{m} \cdot a^{n} &=&a^{m+n} \\\textbf{Power Property} & \left(a^{m}\right)^{n} &=&a^{m \cdot n} \\\textbf{Product to a Power} & (a b)^{m} &=&a^{m} b^{m} \\ \textbf{Quotient Property} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0, m>n \\ & \dfrac{a^{n}}{a^{n}} &=&1, a \neq 0, n>m \\\textbf{Zero Exponent Definition} &a^0&=&1,a\neq 0 \\\textbf{Quotient to a Power Property} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \end{array}\]
Simplificar:\(\dfrac{\left(y^{4}\right)^{2}}{y^{6}}\)
- Contestar
-
\(\begin{array} {ll} & \dfrac{\left(y^{4}\right)^{2}}{y^{6}} \\ \text{Multiply the exponents in the numerator.} & \dfrac{y^{8}}{y^{6}}\\ \text{Subtract the exponents.} &y^{2} \end{array}\)
Simplificar:\(\dfrac{\left(m^{5}\right)^{4}}{m^{7}}\)
- Contestar
-
\(m^{13}\)
Simplificar:\(\dfrac{\left(k^{2}\right)^{6}}{k^{7}}\)
- Contestar
-
\(k^{5}\)
Simplificar:\(\dfrac{b^{12}}{\left(b^{2}\right)^{6}}\)
- Contestar
-
\[\begin{array} {ll} &\dfrac{b^{12}}{\left(b^{2}\right)^{6}} \\ \text{Multiply the exponents in the numerator.} & \dfrac{b^{12}}{b^{12}}\\ \text{Subtract the exponents.} &b^{0} \\ \text{Simplify} & 1\end{array}\]
Observe que después de que simplificamos el denominador en el primer paso, el numerador y el denominador fueron iguales. Entonces el valor final es igual a 1.
Simplificar\(\dfrac{n^{12}}{\left(n^{3}\right)^{4}}\).
- Contestar
-
1
Simplificar\(\dfrac{x^{15}}{\left(x^{3}\right)^{5}}\).
- Contestar
-
1
Simplificar:\(\left(\dfrac{y^{9}}{y^{4}}\right)^{2}\)
- Contestar
-
\[\begin{array} {ll} &\left(\dfrac{y^{9}}{y^{4}}\right)^{2}\\ \text{Remember parentheses come before exponents.} &\\ \text{Notice the bases are the same, so we can simplify} &\left(y^{5}\right)^{2} \\ \text{inside the parentheses. Subtract the exponents.} & \\\text{Multiply the exponents.} &y^{10} \end{array}\]
Simplificar:\(\left(\dfrac{r^{5}}{r^{3}}\right)^{4}\)
- Contestar
-
\(r^{8}\)
Simplificar:\(\left(\dfrac{v^{6}}{v^{4}}\right)^{3}\)
- Contestar
-
\(v^{6}\)
Simplificar:\(\left(\dfrac{j^{2}}{k^{3}}\right)^{4}\)
- Contestar
-
Aquí no podemos simplificar primero dentro de los paréntesis, ya que las bases no son las mismas.
\(\begin{array} {ll} &\left(\dfrac{j^{2}}{k^{3}}\right)^{4}\\ \text{Raise the numerator and denominator to the third power} & \\ \text{using the Quotient to a Power Property,}\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}} &\dfrac{\left(j^{2}\right)^{4}}{\left(k^{3}\right)^{4}}\\ \text{Use the Power Property and simplify.} & \dfrac{j^{8}}{k^{12}} \end{array}\)
Simplificar:\(\left(\dfrac{a^{3}}{b^{2}}\right)^{4}\)
- Contestar
-
\(\dfrac{a^{12}}{b^{8}}\)
Simplificar:\(\left(\dfrac{q^{7}}{r^{5}}\right)^{3}\)
- Contestar
-
\(\dfrac{q^{21}}{r^{15}}\)
Simplificar:\(\left(\dfrac{2 m^{2}}{5 n}\right)^{4}\)
- Contestar
-
\(\begin{array} {ll} &\left(\dfrac{2 m^{2}}{5 n}\right)^{4}\\ \text{Raise the numerator and denominator to the fourth} &\dfrac{\left(2 m^{2}\right)^{4}}{(5 n)^{4}} \\ \text{power, using the Quotient to a Power Property,}\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}} &\dfrac{2^{4}\left(m^{2}\right)^{4}}{5^{4} n^{4}}\\ \text{Use the Power Property and simplify.} & \dfrac{16 m^{8}}{625 n^{4}} \end{array}\)
Simplificar:\(\left(\dfrac{7 x^{3}}{9 y}\right)^{2}\)
- Contestar
-
\(\dfrac{49 x^{6}}{81 y^{2}}\)
Simplificar:\(\left(\dfrac{3 x^{4}}{7 y}\right)^{2}\)
- Contestar
-
\(\dfrac{9 x^{8}}{49 v^{2}}\)
Simplificar:\(\dfrac{\left(x^{3}\right)^{4}\left(x^{2}\right)^{5}}{\left(x^{6}\right)^{5}}\)
- Contestar
-
\(\begin{array}{ll}&\dfrac{\left(x^{3}\right)^{4}\left(x^{2}\right)^{5}}{\left(x^{6}\right)^{5}}\\ \text{Use the Power Property,}\left(a^{m}\right)^{n}=a^{m \cdot n} &\dfrac{\left(x^{12}\right)\left(x^{10}\right)}{\left(x^{30}\right)}\\ \text{Add the exponents in the numerator.} &\dfrac{x^{22}}{x^{30}}\\ \text{Use the Quotient Property,} \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}&\dfrac{1}{x^{8}}\end{array}\)
Simplificar:\(\dfrac{\left(a^{2}\right)^{3}\left(a^{2}\right)^{4}}{\left(a^{4}\right)^{5}}\)
- Contestar
-
\(\dfrac{1}{a^{6}}\)
Simplificar:\(\dfrac{\left(p^{3}\right)^{4}\left(p^{5}\right)^{3}}{\left(p^{7}\right)^{6}}\)
- Contestar
-
\(\dfrac{1}{p^{15}}\)
Simplificar:\(\dfrac{\left(10 p^{3}\right)^{2}}{(5 p)^{3}\left(2 p^{5}\right)^{4}}\)
- Contestar
-
\(\begin{array} {ll} &\dfrac{\left(10 p^{3}\right)^{2}}{(5 p)^{3}\left(2 p^{5}\right)^{4}}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{m} b^{m}&\dfrac{(10)^{2}\left(p^{3}\right)^{2}}{(5)^{3}(p)^{3}(2)^{4}\left(p^{5}\right)^{4}}\\ \text { Use the Power Property, }\left(a^{m}\right)^{n}=a^{m \cdot n}&\dfrac{100 p^{6}}{125 p^{3} \cdot 16 p^{20}}\\ \text { Add the exponents in the denominator. }&\dfrac{100 p^{6}}{125 \cdot 16 p^{23}} \\ \text { Use the Quotient Property, } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}} & \dfrac{100}{125 \cdot 16 p^{17}} \\ \text { Simplify. } & \dfrac{1}{20 p^{17}} \end{array}\)
Simplificar:\(\dfrac{\left(3 r^{3}\right)^{2}\left(r^{3}\right)^{7}}{\left(r^{3}\right)^{3}}\)
- Contestar
-
9\(r^{18}\)
Simplificar:\(\dfrac{\left(2 x^{4}\right)^{5}}{\left(4 x^{3}\right)^{2}\left(x^{3}\right)^{5}}\)
- Contestar
-
\(\dfrac{2}{x}\)
Dividir monomios
Ahora te han introducido todas las propiedades de los exponentes y las has usado para simplificar las expresiones. A continuación, verás cómo usar estas propiedades para dividir los monomios. Posteriormente, los usarás para dividir polinomios.
Encuentra el cociente:\(56 x^{7} \div 8 x^{3}\)
- Contestar
-
\[\begin{array} {ll} &56 x^{7} \div 8 x^{3}\\ \text { Rewrite as a fraction. }&\dfrac{56 x^{7}}{8 x^{3}}\\ \text { Use fraction multiplication. }&\dfrac{56}{8} \cdot \dfrac{x^{7}}{x^{3}}\\ \text { Simplify and use the Quotient Property. }&7 x^{4}\end{array}\]
Encuentra el cociente:\(42y^{9} \div 6 y^{3}\)
- Contestar
-
\(7y^{6}\)
Encuentra el cociente:\(48z^{8} \div 8 z^{2}\)
- Contestar
-
\(6z^{6}\)
Encuentra el cociente:\(\dfrac{45 a^{2} b^{3}}{-5 a b^{5}}\)
- Contestar
-
Cuando dividimos los monomios con más de una variable, escribimos una fracción para cada variable.
\(\begin{array} {ll} &\dfrac{45 a^{2} b^{3}}{-5 a b^{5}}\\ \text { Use fraction multiplication. }&\dfrac{45}{-5} \cdot \dfrac{a^{2}}{a} \cdot \dfrac{b^{3}}{b^{5}}\\\text { Simplify and use the Quotient Property. }&-9 \cdot a \cdot \dfrac{1}{b^{2}}\\\text { Multiply. }&-\dfrac{9 a}{b^{2}}\end{array}\)
Encuentra el cociente:\(\dfrac{-72 a^{7} b^{3}}{8 a^{12} b^{4}}\)
- Contestar
-
\(-\dfrac{9}{a^{5} b}\)
Encuentra el cociente:\(\dfrac{-63 c^{8} d^{3}}{7 c^{12} d^{2}}\)
- Contestar
-
\(\dfrac{-9 d}{c^{4}}\)
Encuentra el cociente:\(\dfrac{24 a^{5} b^{3}}{48 a b^{4}}\)
- Contestar
-
\(\begin{array} {ll} &\dfrac{24 a^{5} b^{3}}{48 a b^{4}}\\ \text { Use fraction multiplication. }&\dfrac{24}{48} \cdot \dfrac{a^{5}}{a} \cdot \dfrac{b^{3}}{b^{4}}\\\text { Simplify and use the Quotient Property. }&\dfrac{1}{2} \cdot a^{4} \cdot \dfrac{1}{b}\\\text { Multiply. }&\dfrac{a^{4}}{2 b}\end{array}\)
Encuentra el cociente:\(\dfrac{16 a^{7} b^{6}}{24 a b^{8}}\)
- Contestar
-
\(\dfrac{2 a^{6}}{3 b^{2}}\)
Encuentra el cociente:\(\dfrac{27 p^{4} q^{7}}{-45 p^{12} q}\)
- Contestar
-
\(-\dfrac{3 q^{6}}{5 p^{8}}\)
Una vez que se familiarice con el proceso y lo haya practicado paso a paso varias veces, es posible que pueda simplificar una fracción en un solo paso.
Encuentra el cociente:\(\dfrac{14 x^{7} y^{12}}{21 x^{11} y^{6}}\)
- Contestar
-
Tenga mucho cuidado de simplificar\(\dfrac{14}{21}\) dividiendo un factor común, y de simplificar las variables restando sus exponentes.
\(\begin{array} {ll} &\dfrac{14 x^{7} y^{12}}{21 x^{11} y^{6}}\\ \text { Simplify and use the Quotient Property. } & \dfrac{2 y^{6}}{3 x^{4}}\end{array}\)
Encuentra el cociente:\(\dfrac{28 x^{5} y^{14}}{49 x^{9} y^{12}}\)
- Contestar
-
\(\dfrac{4 y^{2}}{7 x^{4}}\)
Encuentra el cociente:\(\dfrac{30 m^{5} n^{11}}{48 m^{10} n^{14}}\)
- Contestar
-
\(\dfrac{5}{8 m^{5} n^{3}}\)
En todos los ejemplos hasta el momento, no había trabajo que hacer en el numerador o denominador antes de simplificar la fracción. En el siguiente ejemplo, primero encontraremos el producto de dos monomios en el numerador antes de simplificar la fracción. Esto sigue el orden de las operaciones. Recuerde, una barra de fracciones es un símbolo de agrupación.
Encuentra el cociente:\(\dfrac{\left(6 x^{2} y^{3}\right)\left(5 x^{3} y^{2}\right)}{\left(3 x^{4} y^{5}\right)}\)
- Contestar
-
\(\begin{array} {lc} &\dfrac{\left(6 x^{2} y^{3}\right)\left(5 x^{3} y^{2}\right)}{\left(3 x^{4} y^{5}\right)}\\ \text { Simplify the numerator. }&\dfrac{30 x^{5} y^{5}}{3 x^{4} y^{5}} \\ \text { Simplify. } &10 x \end{array}\)
Encuentra el cociente:\(\dfrac{\left(6 a^{4} b^{5}\right)\left(4 a^{2} b^{5}\right)}{12 a^{5} b^{8}}\)
- Contestar
-
\(2 a b^{2}\)
Encuentra el cociente:\(\dfrac{\left(-12 x^{6} y^{9}\right)\left(-4 x^{5} y^{8}\right)}{-12 x^{10} y^{12}}\)
- Contestar
-
\(-4 x y^{5}\)
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con monomios divididos:
- Expresiones racionales
- Dividir monomios
- Dividiendo Monomios 2
Conceptos clave
- Propiedad de cociente para exponentes:
- Si a es un número real\(a\neq 0\), y m, n son números enteros, entonces:\(\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \text { and } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{m-n}}, n>m\)
- Cero exponente
- Si a es un número distinto de cero, entonces\(a^{0} =1\).
- Cociente a una propiedad de potencia para exponentes:
- Si a y b son números reales\(b\neq 0\), y mm es un número de conteo, entonces:\(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\)
- Para elevar una fracción a una potencia, elevar el numerador y denominador a ese poder.
- Resumen de Exponent Properties
- Si a, b son números reales y m, nm, n son números enteros, entonces\(\begin{array}{lrll} \textbf{Product Property} & a^{m} \cdot a^{n} &=&a^{m+n} \\\textbf{Power Property} & \left(a^{m}\right)^{n} &=&a^{m \cdot n} \\\textbf{Product to a Power} & (a b)^{m} &=&a^{m} b^{m} \\ \textbf{Quotient Property} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0, m>n \\ & \dfrac{a^{n}}{a^{n}} &=&1, a \neq 0, n>m \\\textbf{Zero Exponent Definition} &a^0&=&1,a\neq 0 \\\textbf{Quotient to a Power Property} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \end{array}\)