9.7E: Ejercicios
( \newcommand{\kernel}{\mathrm{null}\,}\)
La práctica hace la perfección
Simplifique las expresiones con raíces superiores
En los siguientes ejercicios, simplifique.
- 3√216
- 4√256
- 5√32
- 3√27
- 4√16
- 5√243
- Contestar
-
- 3
- 2
- 3
- 3√512
- 4√81
- 5√1
- 5√125
- 4√1296
- 5√1024
- Contestar
-
- 5
- 6
- 4
- 3√−8
- 4√−81
- 5√−32
- 3√−64
- 4√−16
- 5√−243
- Contestar
-
- −4
- no real
- −3
- 3√−125
- 4√−1296
- 5√−1024
- 3√−512
- 4√−81
- 5√−1
- Contestar
-
- −8
- no es un número real
- −1
- 5√u5
- 8√v8
- 3√a3
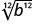
- Contestar
-
- a
- |b|
- 4√y4
- 7√m7
- 8√k8
- 6√p6
- Contestar
-
- |k|
- p
- 3√x9
- 4√y12
- 5√a10
- 3√b27
- Contestar
-
- a2
- b9
- 4√m8
- 5√n20
- 6√r12
- 3√s30
- Contestar
-
- r2
- s10
- 4√16x8
- 6√64y12
- 3√−8c9
- 3√125d15
- Contestar
-
- −2c3
- 5d5
- 3√216a6
- 5√32b20
- 7√128r14
- 4√81s24
- Contestar
-
- 2r2
- 3s6
Utilice la propiedad Product para simplificar expresiones con raíces más altas
En los siguientes ejercicios, simplifique.
- 3√r5
- 4√s10
- 5√u7
- 6√v11
- Contestar
-
- u5√u2
- v6√v5
- 4√m5
- 8√n10
- 5√p8
- 3√q8
- Contestar
-
- p5√p3
- q23√q2
- 4√32
- 5√64
- 3√625
- 6√128
- Contestar
-
- 53√5
- 26√2
- 6√64
- 3√256
- 4√3125
- 3√81
- Contestar
-
- 54√5
- 33√3
- 3√108x5
- 4√48y6
- 5√96a7
- 3√375b4
- Contestar
-
- 2a5√3a2
- 5b3√3b
- 4√405m10
- 5√160n8
- 3√512p5
- 4√324q7
- Contestar
-
- 8p3√p2
- 3q4√4q3
- 3√−864
- 4√−256
- 5√−486
- 6√−64
- Contestar
-
- −35√2
- no real
- 5√−32
- 8√−1
- 3√−8
- 4√−16
- Contestar
-
- −2
- no real
En los siguientes ejercicios, simplifique.
- 3√p11p2
- 4√q17q13
- 5√d12d7
- 8√m12m4
- Contestar
-
- d
- |m|
- 5√u21u11
- 6√v30v12
- 3√r14r5
- 4√c21c9
- Contestar
-
- r2
- ∣c3∣
- 4√644√2
- 5√128x85√2x2
- 3√−6253√5
- 4√80m74√5m
- Contestar
-
- −5
- 4m4√m2
- 3√10502
- 4√486y92y3
- 3√1626
- 4√160r105r3
- Contestar
-
- 33√6
- 2|r|4√2r3
- 3√54a8b3
- 4√64c5d2
- 5√96r11s3
- 6√128u7v3
- Contestar
-
- 2r25√3rs3
- 2u6√2uv3v
- 3√81s8t3
- 4√64p15q12
- 3√625u10v3
- 4√729c21d8
- Contestar
-
- 5u33√5uv
- 3c54√9cd2
En los siguientes ejercicios, simplifique.
- 7√8p+7√8p
- 33√25−3√25
- 3√15q+3√15q
- 24√27−64√27
- Contestar
-
- 23√15q
- −44√27
- 35√9x+75√9x
- 87√3q−27√3q
1.
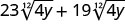
2.
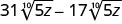
- Contestar
-
1.
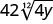
2.
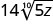
- 3√81−3√192
- 4√512−4√32
- 3√250−3√54
- 4√243−4√1875
- Responder
-
- 53√5−33√2
- −24√3
- 3√128+3√250
- 5√729+5√96
- 4√243+4√1250
- 3√2000+3√54
- Responder
-
- 34√3+54√2
- 133√2
- 3√64a10−3√−216a12
- 4√486u7+4√768u3
- 3√80b5−3√−270b3
- 4√160v10−4√1280v3
- Responder
-
- 2b3√10b2+3b3√10
- 2v24√10v2−44√5v3
En los siguientes ejercicios, simplifique.
4√16
6√64
- Responder
-
2
3√a3
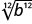
- Responder
-
|b|
3√−8c9
3√125d15
- Responder
-
5d5
3√r5
4√s10
- Responder
-
s24√s2
3√108x5
4√48y6
- Responder
-
2y4√3y2
5√−486
6√−64
- Responder
-
no real
4√644√2
5√128x85√2x2
- Responder
-
2x5√2x
5√96r11s3
6√128u7v3
- Responder
-
2u36√2uv3v
3√81−3√192
4√512−4√32
- Responder
-
44√2
3√64a10−3√−216a12
4√486u7+4√768u3
- Responder
-
3u4√6u3+44√3u3
Matemáticas cotidianas
Crecimiento poblacional La expresión10·xn modela el crecimiento de una población de moho después de n generaciones. Había 10 esporas al inicio, y cada una tenía x descendencia. Así10·xn es el número de crías en la quinta generación. En la quinta generación había 10,240 crías. Simplificar la expresión5√10,24010 para determinar el número de crías de cada espora.
Diseminación de un virus La expresión3·xn modela la propagación de un virus después de n ciclos. Había tres personas originalmente infectadas con el virus, y cada una de ellas infectó x personas. Así3·x4 es el número de personas infectadas en el cuarto ciclo. En el cuarto ciclo se infectaron 1875 personas. Simplificar la expresión4√18753 para determinar el número de personas infectadas por cada persona.
- Responder
-
5
Ejercicios de escritura
Explica cómo lo sabes5√x10=x2.
4√−64Explique por qué no es un número real sino3√−64 que sí.
- Responder
-
Las respuestas pueden variar.
Autocomprobación
ⓐ Después de completar los ejercicios, usa esta lista de verificación para evaluar tu dominio de los objetivos de esta sección.
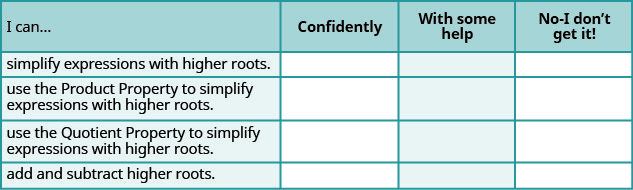
ⓑ ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?


