10.4: Resolver aplicaciones modeladas por ecuaciones cuadráticas
( \newcommand{\kernel}{\mathrm{null}\,}\)
Al final de esta sección, podrás:
- Resolver aplicaciones modeladas por ecuaciones cuadráticas
Antes de comenzar, toma este cuestionario de preparación.
- La suma de dos números impares consecutivos es −100. Encuentra los números.
Si te perdiste este problema, revisa [enlace]. - El área del mural triangular es de 64 pies cuadrados. La base es de 16 pies. Encuentra la altura.
Si te perdiste este problema, revisa [enlace]. - Encuentra la longitud de la hipotenusa de un triángulo rectángulo con patas de 5 pulgadas y 12 pulgadas.
Si te perdiste este problema, revisa [enlace].
Resolver Aplicaciones de la Fórmula Cuadrática
Resolvimos algunas aplicaciones que son modeladas por ecuaciones cuadráticas antes, cuando el único método que teníamos para resolverlas era factorizar. Ahora que tenemos más métodos para resolver ecuaciones cuadráticas, vamos a echar otro vistazo a las aplicaciones. Para comenzar, copiaremos nuestra estrategia habitual de resolución de problemas aquí para que podamos seguir los pasos.
- Lee el problema. Asegúrate de que todas las palabras e ideas sean entendidas.
- Identificar lo que estamos buscando.
- Nombra lo que estamos buscando. Elija una variable para representar esa cantidad.
- Traducir en una ecuación. Puede ser útil reafirmar el problema en una oración con toda la información importante. Después, traducir la oración en inglés a una ecuación álgebra.
- Resolver la ecuación usando buenas técnicas de álgebra.
- Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
- Contesta la pregunta con una oración completa.
Hemos resuelto aplicaciones numéricas que involucraban enteros pares consecutivos y enteros impares consecutivos modelando la situación con ecuaciones lineales. Recuerda, notamos que cada entero par es 2 más que el número que lo precede. Si llamamos al primero n, entonces el siguiente esn+2. The next one would be n+2+2 or n+4. This is also true when we use odd integers. One set of even integers and one set of odd integers are shown below.
Consecutive even integersConsecutive odd integers64,66,6877,79,81n1steven numbern1stodd numbern+22ndeven numbern+22ndodd numbern+43rdeven numbern+43rdodd number
Algunas aplicaciones de enteros impares consecutivos o enteros pares consecutivos se modelan mediante ecuaciones cuadráticas. La notación anterior será útil a medida que nombre las variables.
El producto de dos enteros impares consecutivos es 195. Encuentra los enteros.
- Contestar
-
Paso 1. Lee el problema. Paso 2. Identificar lo que estamos buscando. Estamos buscando dos enteros impares consecutivos. Paso 3. Nombra lo que estamos buscando. Dejar quen= el primer entero impar.
n+2=el siguiente entero imparPaso 4. Traducir en una ecuación. Exponga el problema en una frase. “El producto de dos enteros impares consecutivos es 195”. El producto del primer entero impar y el segundo entero impar es 195. Traducir en una ecuación. 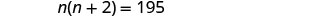
Paso 5. Resuelve la ecuación. Distribuir. 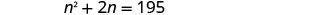
Restar 195 para obtener la ecuación en forma estándar. 
Identificar los valores a, b, c. 
Escribe la ecuación cuadrática. 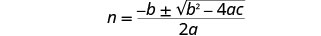
Después sustituya en los valores de a, b, c. 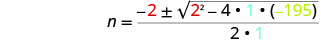
Simplificar. 
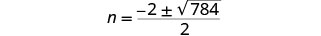
Simplifica lo radical. 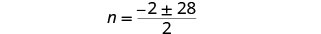
Reescribe para mostrar dos soluciones. 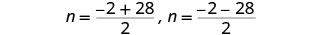
Resuelve cada ecuación. 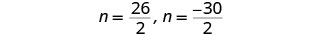
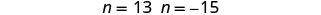
Hay dos valores de n que son soluciones. Esto nos dará dos pares de enteros impares consecutivos para nuestra solución. Primer entero impar n=13
siguiente entero impar n+2
13+2
15Primer entero impar n=−15
siguiente entero impar n+2
−15+2
−13Paso 6. Consulta la respuesta.
¿Funcionan estos pares?
¿Son enteros impares consecutivos?
¿Su producto es 195?13, 15, sí −13, −15, sí
1315=195, sí −13 (−15) =195, sí
Paso 7. Contesta la pregunta. Los dos números enteros impares consecutivos cuyo producto es 195 son 13, 15 y −13, −15.
El producto de dos enteros impares consecutivos es 99. Encuentra los enteros.
- Contestar
-
Dos números impares consecutivos cuyo producto es 99 son 9 y 11, y −9 y −11.
El producto de dos enteros impares consecutivos es 168. Encuentra los enteros.
- Contestar
-
Dos números pares consecutivos cuyo producto es 168 son 12 y 14, y −12 y −14.
Usaremos la fórmula para el área de un triángulo para resolver el siguiente ejemplo.
Para un triángulo con base b y altura h, el área, A, viene dada por la fórmulaA=12bh.
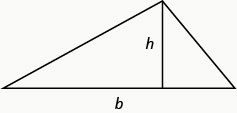
Recordemos que, cuando resolvemos aplicaciones de geometría, es útil dibujar la figura.
Un arquitecto está diseñando la entrada de un restaurante. Ella quiere poner una ventana triangular por encima de la puerta. Debido a restricciones energéticas, la ventana puede tener un área de 120 pies cuadrados y el arquitecto quiere que el ancho sea de 4 pies más del doble de la altura. Encuentra la altura y anchura de la ventana.
- Contestar
-
Paso 1. Lee el problema.
Dibuja un cuadro.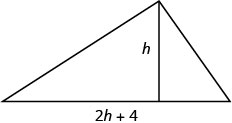
Paso 2. Identificar lo que estamos buscando. Estamos buscando la altura y anchura. Paso 3. Nombra lo que estamos buscando. Deja queh= la altura del triángulo.
2h+4=el ancho del triánguloPaso 4. Traducir. Conocemos la zona. Escribe la fórmula para el área de un triángulo.

Paso 5. Resuelve la ecuación. Sustituto en los valores. 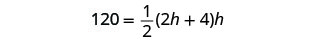
Distribuir. 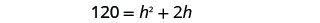
Esta es una ecuación cuadrática, reescribirla en forma estándar. 
Resuelve la ecuación usando la Fórmula Cuadrática. Identificar los valores a, b, c. 
Escribe la ecuación cuadrática. 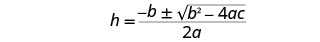
Después sustituya en los valores de a, b, c. 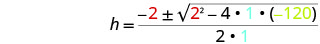
Simplificar. 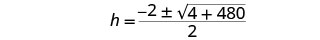
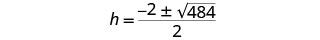
Simplifica lo radical. 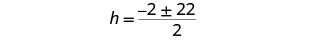
Reescribe para mostrar dos soluciones. 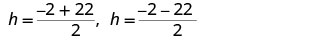
Simplificar. 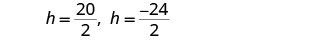
Dado que h es la altura de una ventana, un valor deh=−12 no tiene sentido. 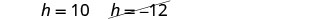
La altura del triángulo:h=10
El ancho del triángulo:2h+4
2⋅10+4
24Paso 6. Consulta la respuesta. ¿Un triángulo con una altura 10 y un ancho 24 tiene área 120? Sí. Paso 7. Contesta la pregunta. La altura de la ventana triangular es de 10 pies y el ancho es de 24 pies. Observe que las soluciones fueron números enteros. Eso nos dice que podríamos haber resuelto la ecuación factorizando.
Cuando escribimos la ecuación en forma estándarh2+2h−120=0,, podríamos haberla factorizado. Si lo hubiéramos hecho, habríamos resuelto la ecuación(h+12)(h−10)=0.
Encuentra las dimensiones de un triángulo cuyo ancho es cuatro más de seis veces su altura y tiene un área de 208 pulgadas cuadradas.
- Contestar
-
La altura del triángulo es de 8 pulgadas y el ancho es de 52 pulgadas.
Si un triángulo que tiene un área de 110 pies cuadrados tiene una altura que es dos pies menor que el doble de ancho, ¿cuáles son sus dimensiones?
- Contestar
-
La altura del triángulo es de 20 pies y el ancho es de 11 pies.
En los dos ejemplos anteriores, el número en el radical en la Fórmula Cuadrática era un cuadrado perfecto y así las soluciones fueron números racionales. Si obtenemos un número irracional como solución a un problema de aplicación, utilizaremos una calculadora para obtener un valor aproximado.
El Teorema de Pitágoras da la relación entre las piernas y la hipotenusa de un triángulo rectángulo. Utilizaremos el Teorema de Pitágoras para resolver el siguiente ejemplo.
En cualquier triángulo rectángulo, donde a y b son las longitudes de las piernas y c es la longitud de la hipotenusa,a2+b2=c2
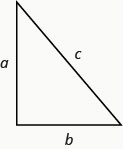
René está configurando una pantalla de luces navideñas. Quiere hacer un 'árbol' en forma de dos triángulos rectos, como se muestra a continuación, y tiene dos cadenas de luces de 10 pies para usar para los costados. Él sujetará las luces a la parte superior de un poste y a dos estacas en el suelo. Quiere que la altura del poste sea la misma que la distancia desde la base del poste hasta cada estaca. ¿Qué tan alto debe ser el poste?
- Contestar
-
Paso 1. Lee el problema. Dibuja un cuadro 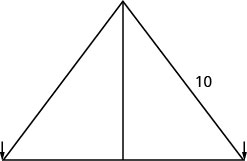
Paso 2. Identificar lo que estamos buscando. Estamos buscando la altura del poste. Paso 3. Nombra lo que estamos buscando. La distancia desde la base del poste a cualquiera de las estacas es la misma que la altura del poste. Deja quex= la altura del poste.
x=la distancia desde el poste a la estacaCada lado es un triángulo rectángulo. Dibujamos una imagen de una de ellas. 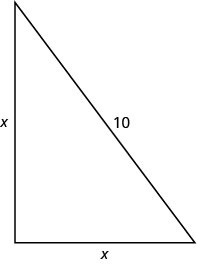
Paso 4. Traducir en una ecuación. Podemos usar el Teorema de Pitágoras para resolver para x. Escribe el Teorema de Pitágoras. a2+b2=c2 Paso 5. Resuelve la ecuación. Sustituto. x2+x2=102 Simplificar. 2x2=100 Dividir por 2 para aislar la variable. 2x22=1002 Simplificar. x2=50 Utilice la Propiedad Raíz Cuadrada. x=±√50 Simplifica lo radical. x=±5√2 Reescribe para mostrar dos soluciones. x=5√2
⧸x=−5√2Aproximar este número a la décima más cercana con una calculadora. x≈7.1 Paso 6. Consulta la respuesta.
Consulta por tu cuenta en el Teorema de Pitágoras.Paso 7. Contesta la pregunta. El poste debe medir aproximadamente 7.1 pies de altura.
El sol proyecta una sombra desde un asta de bandera. La altura del asta de bandera es tres veces la longitud de su sombra. La distancia entre el extremo de la sombra y la parte superior del asta de la bandera es de 20 pies. Encuentra la longitud de la sombra y la longitud del asta de la bandera. Redondear a la décima de pie más cercana.
- Contestar
-
La longitud de la sombra es de 6.3 pies y la longitud del asta de la bandera es de 18.9 pies.
La distancia entre las esquinas opuestas de un campo rectangular es cuatro más que el ancho del campo. La longitud del campo es el doble de su ancho. Encuentra la distancia entre las esquinas opuestas. Redondear a la décima más cercana.
- Contestar
-
La distancia a la esquina opuesta es de 3.2.
Mike quiere poner 150 pies cuadrados de césped artificial en su patio delantero. Esta es la superficie máxima de césped artificial permitida por su asociación de propietarios. Quiere tener un área rectangular de césped con longitud un pie menos de tres veces el ancho. Encuentra el largo y ancho. Redondear a la décima de pie más cercana.
- Contestar
-
Paso 1. Lee el problema. Dibuja un cuadro. 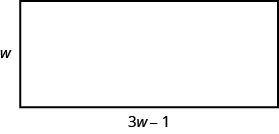
Paso 2. Identificar lo que estamos buscando. Estamos buscando el largo y ancho. Paso 3. Nombra lo que estamos buscando. Deja quew= el ancho del rectángulo.
3w−1=la longitud del rectánguloPaso 4. Traducir en una ecuación.
Conocemos la zona. Escribe la fórmula para el área de un rectángulo.
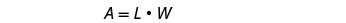
Paso 5. Resuelve la ecuación. Sustituto en los valores. 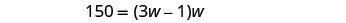
Distribuir. 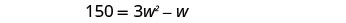
Esta es una ecuación cuadrática, reescribirla en forma estándar. 
Resuelve la ecuación usando la Fórmula Cuadrática. Identificar los valores a, b, c. 
Escribe la Fórmula Cuadrática. 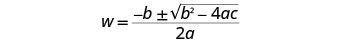
Después sustituya en los valores de a, b, c. 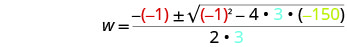
Simplificar. 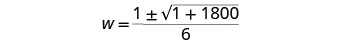
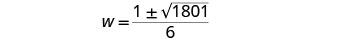
Reescribe para mostrar dos soluciones. 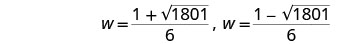
Aproximar las respuestas usando una calculadora.
Eliminamos la solución negativa para el ancho.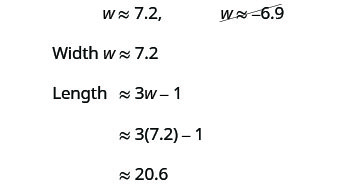
Paso 6. Consulta la respuesta.
Asegúrate de que las respuestas tengan sentido.Paso 7. Contesta la pregunta. El ancho del rectángulo es aproximadamente 7.2 pies y el largo 20.6 pies.
La longitud de un huerto rectangular de 200 pies cuadrados es cuatro pies menos que el doble de ancho. Encuentra el largo y ancho del jardín. Redonda a la décima más cercana de un pie..
- Contestar
-
El ancho del jardín es de 11 pies y el largo es de 18 pies.
Un mantel rectangular tiene una superficie de 80 pies cuadrados. El ancho es 5 pies más corto que el largo. ¿Cuál es el largo y ancho del mantel? Redondear a la décima de pie más cercana.
- Contestar
-
El ancho del mantel es de 6.8 pies y el largo es de 11.8 pies.
La altura de un proyectil disparado hacia arriba es modelada por una ecuación cuadrática. La velocidad inicial,\(v_{0}\), impulsa al objeto hacia arriba hasta que la gravedad hace que el objeto vuelva a caer.
La altura en pies, h, de un objeto disparado hacia arriba al aire con velocidad inicialv0, después de t segundos viene dada por la fórmula:
h=−16t2+v0t
Podemos usar la fórmula para el movimiento de proyectiles para encontrar cuántos segundos tardará un fuego artificial en alcanzar una altura específica.
Un fuego artificial se dispara hacia arriba con una velocidad inicial de 130 pies por segundo. ¿Cuántos segundos tardará en alcanzar una altura de 260 pies? Redondear a la décima de segundo más cercana.
- Contestar
-
Paso 1. Lee el problema. Paso 2. Identificar lo que estamos buscando. Estamos buscando el número de segundos, que es el tiempo. Paso 3. Nombra lo que estamos buscando. Deje quet= el número de segundos. Paso 4. Traducir en una ecuación. Usa la fórmula. h=−16t2+v0t Paso 5. Resuelve la ecuación.
Sabemos que la velocidadv0 es de 130 pies por segundo.La altura es de 260 pies. Sustituir los valores. 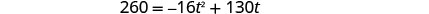
Esta es una ecuación cuadrática, reescribirla en forma estándar. 
Resuelve la ecuación usando la Fórmula Cuadrática. Identificar los valores a, b, c. 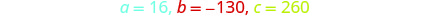
Escribe la Fórmula Cuadrática. 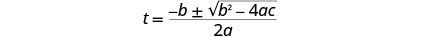
Después sustituya en los valores de a, b, c. 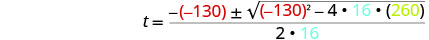
Simplificar. 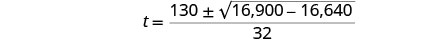
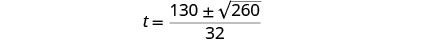
Reescribe para mostrar dos soluciones. 
Aproximar las respuestas con una calculadora. t≈4.6segundos,t≈3.6 Paso 6. Consulta la respuesta.
El cheque se te deja a ti.Paso 7. Contesta la pregunta. Los fuegos artificiales subirán y luego volverán a caer.
A medida que los fuegos artificiales suben, alcanzará los 260 pies después de
aproximadamente 3.6 segundos. También pasará esa
altura en el camino hacia abajo a 4.6 segundos.

Una flecha es disparada desde el suelo al aire a una velocidad inicial de 108 pies/seg. Usa la fórmulah=−16t2+v0t para determinar cuándo la flecha estará a 180 pies del suelo. Redondear la décima de segundo más cercana.
- Contestar
-
La flecha llegará a 180 en su camino hacia arriba en 3 segundos, y en el camino hacia abajo en 3.8 segundos.
Un hombre lanza una pelota al aire con una velocidad de 96 pies/seg. Usa la fórmulah=−16t2+v0t para determinar cuándo la altura de la pelota será de 48 pies. Redondear a la décima de segundo más cercana.
- Contestar
-
El balón llegará a 48 pies en su camino hacia arriba en .6 segundos y en el camino hacia abajo en 5.5 segundos.
Acceda a estos recursos en línea para obtener instrucción y práctica adicionales para resolver problemas de palabras usando la ecuación cuadrática:
Conceptos clave
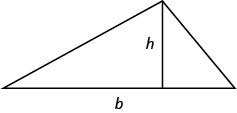
- Área de un Triángulo Para un triángulo con base, b y altura, h, el área, A, viene dada por la fórmula:A=12bh
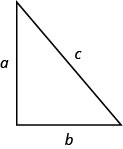
- Teorema de Pitágoras En cualquier triángulo rectángulo, donde a y b son las longitudes de las piernas, y c es la longitud de la hipotenusa,a2+b2=c2
- Movimiento del proyectil La altura en pies, h, de un objeto disparado hacia arriba en el aire con velocidad inicialv0,, después de tt segundos puede modelarse mediante la fórmula
h=−16t2+v0t
Glosario
- enteros pares consecutivos
- Los enteros pares consecutivos son enteros pares que siguen uno tras otro. Si un número entero par está representado por n, el siguiente entero par consecutivo esn+2, y el siguiente después de eso esn+4.
- enteros impares consecutivos
- Los enteros impares consecutivos son enteros impares que siguen uno tras otro. Si un entero impar se representa por n, el siguiente entero impar consecutivo esn+2, y el siguiente después de eso esn+4.


