3.1: Clases de equivalencia de enteros y simetrías

Investiguemos ahora algunas estructuras matemáticas que pueden ser vistas como conjuntos con operaciones únicas.

El mod de enteros\(n\)

Los enteros mod se\(n\) han vuelto indispensables en la teoría y aplicaciones del álgebra. En matemáticas se utilizan en criptografía, teoría de codificación y detección de errores en los códigos de identificación.

Ya hemos visto que dos enteros\(a\) y\(b\) son equivalentes mod\(n\) si\(n\) divide\(a - b\text{.}\) Los enteros mod\(n\) también particionan\({\mathbb Z}\) en\(n\) diferentes clases de equivalencia; denotaremos el conjunto de estas clases de equivalencia por\({\mathbb Z}_n\text{.}\) Considerar los enteros módulo\(12\) y la partición correspondiente de los enteros:

\ begin {alinear*} {[0]} & =\ {\ ldots, -12, 0, 12, 24,\ ldots\},\\ {[1]} & =\ {\ ldots, -11, 1, 13, 25,\ ldots\},\\ &\ vdots\\ {[11]} & =\ {\ ldots, -1, 11, 23, 35,\ lldots, -1, 11, 23, 35,\ lldots puntos\}\ texto {.} \ end {alinear*}

Cuando no pueda surgir confusión, utilizaremos\(0, 1, \ldots, 11\) para indicar las clases de equivalencia\({[0]}, {[1]}, \ldots, {[11]}\) respectivamente. Podemos hacer aritmética en\({\mathbb Z}_n\text{.}\) Para dos enteros\(a\) y\(b\text{,}\) definir módulo de suma\(n\) para ser es\((a + b) \pmod{n}\text{;}\) decir, el resto cuando\(a + b\) se divide por\(n\text{.}\) Similarmente, módulo de multiplicación\(n\) se define como\((a b) \pmod{ n}\text{,}\) el resto cuando\(a b\) es dividido por\(n\text{.}\)

Ejemplo\(3.1\)

Los siguientes ejemplos ilustran el módulo aritmético entero\(n\text{:}\)

\ begin {align*} 7 + 4 &\ equiv 1\ pmod {5} & 7\ cdot 3 &\ equiv 1\ pmod {5}\\ 3 + 5 &\ equiv 0\ pmod {8} & 3\ cdot 5 &\ equiv 7\ pmod {8}\ 3 + 4 &\ equiv 7\ pmod {12} & 3\ cdot 4 &\ equiv 0\ pmod {12}\ texto {.} \ end {alinear*}

Solución

En particular, observe que es posible que el producto de dos números distintos de cero módulo\(n\) pueda ser equivalente a\(0\) módulo\(n\text{.}\)

Ejemplo\ 3.2\)

La mayoría, pero no todas, de las leyes habituales de la aritmética se mantienen para suma y multiplicación en\({\mathbb Z}_n\text{.}\) Por ejemplo, no es necesariamente cierto que haya un inverso multiplicativo. Considere la tabla de multiplicación para\({\mathbb Z}_8\) en la Figura 3.3.

Solución

Observe que\(2\text{,}\)\(4\text{,}\) y\(6\) no tienen inversas multiplicativas; es decir, para\(n = 2\text{,}\)\(4\text{,}\) o no\(6\text{,}\) hay entero\(k\) tal que\(k n \equiv 1 \pmod{ 8}\text{.}\)

\[ \begin{array}{c|cccccccc} \cdot & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ \hline 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ 2 & 0 & 2 & 4 & 6 & 0 & 2 & 4 & 6 \\ 3 & 0 & 3 & 6 & 1 & 4 & 7 & 2 & 5 \\ 4 & 0 & 4 & 0 & 4 & 0 & 4 & 0 & 4 \\ 5 & 0 & 5 & 2 & 7 & 4 & 1 & 6 & 3 \\ 6 & 0 & 6 & 4 & 2 & 0 & 6 & 4 & 2 \\ 7 & 0 & 7 & 6 & 5 & 4 & 3 & 2 & 1 \end{array} \nonumber \]

\(Figure \text { } 3.3\). Tabla de multiplicación para\({\mathbb Z_8}\)

Proposición\(3.4\)

Dejar\({\mathbb Z}_n\) ser el conjunto de clases de equivalencia de los enteros mod\(n\) y\(a, b, c \in {\mathbb Z}_n\text{.}\)

1. La suma y la multiplicación son conmutativas:

   \ begin {align*} a + b &\ equiv b + a\ pmod {n}\\ a b &\ equiv b a\ pmod {n}\ text {.} \ end {alinear*}

2. La suma y la multiplicación son asociativas:

   \ begin {align*} (a + b) + c &\ equiv a + (b + c)\ pmod {n}\\ (a b) c &\ equiv a (b c)\ pmod {n}\ text {.} \ end {alinear*}

3. Hay identidades tanto aditivas como multiplicativas:

   \ begin {align*} a + 0 &\ equiv a\ pmod {n}\\ a\ cdot 1 &\ equiv a\ pmod {n}\ text {.} \ end {alinear*}

4. La multiplicación distribuye sobre la suma:

   \[ a (b + c) \equiv a b + a c \pmod{ n}\text{.} \nonumber \]

5. Por cada entero\(a\) hay una inversa aditiva\(-a\text{:}\)

   \[ a + (-a) \equiv 0 \pmod{ n}\text{.} \nonumber \]

6. Dejar\(a\) ser un entero distinto de cero. Entonces\(\gcd(a,n) = 1\) si y solo si existe una inversa multiplicativa\(b\) para\(a \pmod{n}\text{;}\) eso es, un entero distinto de cero\(b\) tal que

   \[ a b \equiv 1 \pmod{ n}\text{.} \nonumber \]

Prueba

Demostraremos (1) y (6) y dejaremos que las propiedades restantes sean comprobadas en los ejercicios.

(1) La suma y la multiplicación son módulo conmutativo\(n\) ya que el resto de\(a + b\) dividido por\(n\) es el mismo que el resto de\(b + a\) dividido por\(n\text{.}\)

(6) Supongamos que\(\gcd(a, n) = 1\text{.}\) Entonces existen enteros\(r\) y\(s\) tal que\(ar + ns = 1\text{.}\) Dado\(ns = 1 - ar\text{,}\) que debe darse el caso que\(ar \equiv 1 \pmod{n}\text{.}\) Dejar\(b\) ser la clase de equivalencia de\(r\text{,}\)\(a b \equiv 1\pmod{n}\text{.}\)

Por el contrario, supongamos que existe un entero\(b\) tal que\(ab \equiv 1 \pmod{ n}\text{.}\)\(ab -1\text{,}\) Entonces\(n\) divide así hay un entero\(k\) tal que\(ab - nk = 1\text{.}\) Let\(d = \gcd(a,n)\text{.}\) Desde\(d\) divide también\(ab - nk\text{,}\)\(d\) debe dividir\(1\text{;}\) por lo tanto,\(d = 1\text{.}\)

Simetrías

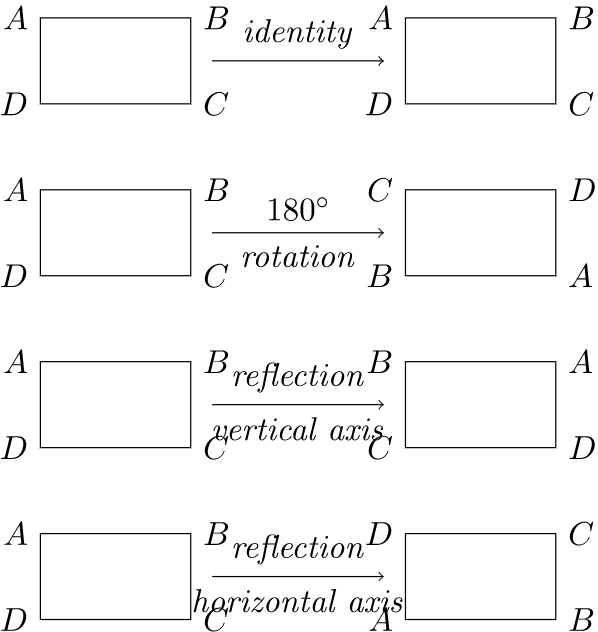
\(Figure \text { } 3.5.\) Rigid motions of a rectangle

A symmetry of a geometric figure is a rearrangement of the figure preserving the arrangement of its sides and vertices as well as its distances and angles. A map from the plane to itself preserving the symmetry of an object is called a rigid motion. For example, if we look at the rectangle in Figure 3.5, it is easy to see that a rotation of \(180^{\circ}\) or \(360^{\circ}\) returns a rectangle in the plane with the same orientation as the original rectangle and the same relationship among the vertices. A reflection of the rectangle across either the vertical axis or the horizontal axis can also be seen to be a symmetry. However, a \(90^{\circ}\) rotation in either direction cannot be a symmetry unless the rectangle is a square.

\(Figure \text { } 3.6.\) Symmetries of a triangle

Let us find the symmetries of the equilateral triangle \(\bigtriangleup ABC\text{.}\) To find a symmetry of \(\bigtriangleup ABC\text{,}\) we must first examine the permutations of the vertices \(A\text{,}\) \(B\text{,}\) and \(C\) and then ask if a permutation extends to a symmetry of the triangle. Recall that a permutation of a set \(S\) is a one-to-one and onto map \(\pi :S \rightarrow S\text{.}\) The three vertices have \(3! = 6\) permutations, so the triangle has at most six symmetries. To see that there are six permutations, observe there are three different possibilities for the first vertex, and two for the second, and the remaining vertex is determined by the placement of the first two. So we have \(3 \cdot 2 \cdot 1 = 3! = 6\) different arrangements. To denote the permutation of the vertices of an equilateral triangle that sends \(A\) to \(B\text{,}\) \(B\) to \(C\text{,}\) and \(C\) to \(A\text{,}\) we write the array

\[ \begin{pmatrix} A & B & C \\ B & C & A \end{pmatrix}\text{.} \nonumber \]

Notice that this particular permutation corresponds to the rigid motion of rotating the triangle by \(120^{\circ}\) in a clockwise direction. In fact, every permutation gives rise to a symmetry of the triangle. All of these symmetries are shown in Figure 3.6.

A natural question to ask is what happens if one motion of the triangle \(\bigtriangleup ABC\) is followed by another. Which symmetry is \(\mu_1 \rho_1\text{;}\) that is, what happens when we do the permutation \(\rho_1\) and then the permutation \(\mu_1\text{?}\) Remember that we are composing functions here. Although we usually multiply left to right, we compose functions right to left. We have

\begin{align*} (\mu_1 \rho_1)(A) & = \mu_1( \rho_1( A ) ) = \mu_1( B ) = C\\ (\mu_1 \rho_1)(B) & = \mu_1( \rho_1( B ) ) = \mu_1( C ) = B\\ (\mu_1 \rho_1)(C) & = \mu_1( \rho_1( C ) ) = \mu_1( A ) = A\text{.} \end{align*}

This is the same symmetry as \(\mu_2\text{.}\) Suppose we do these motions in the opposite order, \(\rho_1\) then \(\mu_1\text{.}\) It is easy to determine that this is the same as the symmetry \(\mu_3\text{;}\) hence, \(\rho_1 \mu_1 \neq \mu_1 \rho_1\text{.}\) A multiplication table for the symmetries of an equilateral triangle \(\bigtriangleup ABC\) is given in Figure 3.7.

Notice that in the multiplication table for the symmetries of an equilateral triangle, for every motion of the triangle \(\alpha\) there is another motion \(\beta\) such that \(\alpha \beta = \text { id }\text{;}\) that is, for every motion there is another motion that takes the triangle back to its original orientation.

\[ \begin{array}{c|cccccc} \circ & \text { id } & \rho_1 & \rho_2 & \mu_1 & \mu_2 & \mu_3 \\ \hline \text { id } & \text { id } & \rho_1 & \rho_2 & \mu_1 & \mu_2 & \mu_3 \\ \rho_1 & \rho_1 & \rho_2 & \text { id } & \mu_3 & \mu_1 & \mu_2 \\ \rho_2 & \rho_2 & \text { id } & \rho_1 & \mu_2 & \mu_3 & \mu_1 \\ \mu_1 & \mu_1 & \mu_2 & \mu_3 & \text { id } & \rho_1& \rho_2\\ \mu_2 & \mu_2 & \mu_3 & \mu_1 & \rho_2 & \text { id } & \rho_1\\ \mu_3 & \mu_3 & \mu_1 & \mu_2 & \rho_1 & \rho_2& \text { id } \end{array} \nonumber \]

\(Figure \text { } 3.7\). Symmetries of an equilateral triangle