11.2: Los Teormos del Isomorfismo

Aunque no es evidente al principio, los grupos factoriales corresponden exactamente a imágenes homomórficas, y podemos utilizar grupos factoriales para estudiar homomorfismos. Ya sabemos que con cada homomorfismo grupal\(\phi: G \rightarrow H\) podemos asociar un subgrupo normal de\(G\text{,}\)\(\ker \phi\text{.}\) Lo contrario también es cierto; es decir, cada subgrupo normal de un grupo\(G\) da lugar al homomorfismo de grupos.

Dejar\(H\) ser un subgrupo normal de\(G\text{.}\) Definir el homomorfismo natural o canónico

\[ \phi : G \rightarrow G/H \nonumber \]

por

\[ \phi(g) = gH\text{.} \nonumber \]

Esto es efectivamente un homomorfismo, ya que

\[ \phi( g_1 g_2 ) = g_1 g_2 H = g_1 H g_2 H = \phi( g_1) \phi( g_2 )\text{.} \nonumber \]

El núcleo de este homomorfismo es\(H\text{.}\) Los siguientes teoremas describen las relaciones entre los homomorfismos grupales, subgrupos normales y grupos factoriales.

Teorema\(11.10\). First Isomorphism Theorem

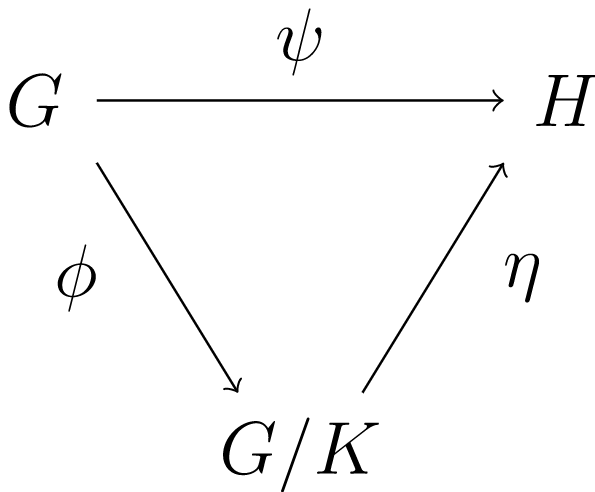
Si\(\psi : G \rightarrow H\) es un homomorfismo grupal con\(K =\ker \psi\text{,}\) entonces\(K\) es normal en\(G\text{.}\) Let\(\phi: G \rightarrow G/K\) be the canonical homomorfism. Entonces existe un isomorfismo único\(\eta: G/K \rightarrow \psi(G)\) tal que\(\psi = \eta \phi\text{.}\)

Prueba

Ya sabemos que\(K\) es normal en\(G\text{.}\) Definir\(\eta: G/K \rightarrow \psi(G)\) por Primero\(\eta(gK) = \psi(g)\text{.}\) mostramos que\(\eta\) es un mapa bien definido. Si\(g_1 K =g_2 K\text{,}\) entonces para algunos en\(k \in K\text{,}\)\(g_1 k=g_2\text{;}\) consecuencia,

\[ \eta(g_1 K) = \psi(g_1) = \psi(g_1) \psi(k) = \psi(g_1k) = \psi(g_2) = \eta(g_2 K)\text{.} \nonumber \]

Así,\(\eta\) no depende de la elección de los representantes del coset y el mapa\(\eta: G/K \rightarrow \psi(G)\) se define de manera única ya que también\(\psi = \eta \phi\text{.}\) debemos mostrar que\(\eta\) es un homomorfismo. En efecto,

\ begin {align*}\ eta (G_1k G_2k) & =\ eta (g_1 G_2k)\\ & =\ psi (g_1 g_2)\\ & =\ psi (g_1)\ psi (g_2)\\ & =\ eta (G_1k)\ eta (G_2k)\ text {.} \ end {alinear*}

Claramente,\(\eta\) es sobre\(\psi( G)\text{.}\) Demostrar que\(\eta\) es uno-a-uno, supongamos que\(\eta(g_1 K) = \eta(g_2 K)\text{.}\) Entonces\(\psi(g_1) = \psi(g_2)\text{.}\) Esto implica que\(\psi( g_1^{-1} g_2 ) = e\text{,}\) o\(g_1^{-1} g_2\) está en el núcleo de\(\psi\text{;}\) ahí, es\(g_1^{-1} g_2K = K\text{;}\) decir,\(g_1K =g_2K\text{.}\)

Los matemáticos suelen utilizar diagramas llamados diagramas conmutativos para describir tales teoremas. El siguiente diagrama “conmuta” desde\(\psi = \eta \phi\text{.}\)

Ejemplo\(11.11\)

Dejar\(G\) ser un grupo cíclico con generador\(g\text{.}\) Definir un mapa\(\phi : {\mathbb Z} \rightarrow G\) por\(n \mapsto g^n\text{.}\)

Solución

Este mapa es un homomorfismo surytivo desde

\[ \phi( m + n) = g^{m+n} = g^m g^n = \phi(m) \phi(n)\text{.} \nonumber \]

Claramente\(\phi\) está sobre. Si\(|g| = m\text{,}\) entonces\(g^m = e\text{.}\) De ahí,\(\ker \phi = m {\mathbb Z}\) y\({\mathbb Z} / \ker \phi = {\mathbb Z} / m {\mathbb Z} \cong G\text{.}\) Por otro lado, si el orden de\(g\) es infinito, entonces\(\ker \phi = 0\) y\(\phi\) es un isomorfismo de\(G\) y\({\mathbb Z}\text{.}\) Por lo tanto, dos grupos cíclicos son isomórficos exactamente cuando tienen el mismo orden. Hasta el isomorfismo, los únicos grupos cíclicos son\({\mathbb Z}\) y\({\mathbb Z}_n\text{.}\)

Teorema\(11.12\)

Dejar\(H\) ser un subgrupo de un grupo\(G\) (no necesariamente normal en\(G\)) y\(N\) un subgrupo normal de\(G\text{.}\) Entonces\(HN\) es un subgrupo de\(G\text{,}\)\(H \cap N\) es un subgrupo normal de\(H\text{,}\) y

\[ H / H \cap N \cong HN /N\text{.} \nonumber \]

Prueba

Primero mostraremos que\(HN = \{ hn : h \in H, n \in N \}\) es un subgrupo de\(G\text{.}\) Supongamos que\(h_1 n_1, h_2 n_2 \in HN\text{.}\) ya\(N\) es normal,\((h_2)^{-1} n_1 h_2 \in N\text{.}\) Así

\[ (h_1 n_1)(h_2 n_2) = h_1 h_2 ( (h_2)^{-1} n_1 h_2 )n_2 \nonumber \]

está en\(HN\text{.}\) La inversa de\(hn \in HN\) está en\(HN\) desde

\[ ( hn )^{-1} = n^{-1 } h^{-1} = h^{-1} (h n^{-1} h^{-1} )\text{.} \nonumber \]

A continuación, demostramos que\(H \cap N\) es normal en\(H\text{.}\) Let\(h \in H\) y\(n \in H \cap N\text{.}\) Entonces\(h^{-1} n h \in H\) ya que cada elemento está en\(H\text{.}\) También,\(h^{-1} n h \in N\) ya que\(N\) es normal en\(G\text{;}\) por lo tanto,\(h^{-1} n h \in H \cap N\text{.}\)

Ahora definimos un mapa\(\phi\) de\(H\) a\(HN / N\) por\(h \mapsto h N\text{.}\) El mapa\(\phi\) es onto, ya que cualquier coset\(h n N = h N\) es la imagen de\(h\) en También\(H\text{.}\) sabemos que\(\phi\) es un homomorfismo porque

\[ \phi( h h') = h h' N = h N h' N = \phi( h ) \phi( h')\text{.} \nonumber \]

Por el primer teorema del isomorfismo, la imagen de\(\phi\) es isomorfa a\(H / \ker \phi\text{;}\) esto es,

\[ HN/N = \phi(H) \cong H / \ker \phi\text{.} \nonumber \]

Desde

\[ \ker \phi = \{ h \in H : h \in N \} = H \cap N\text{,} \nonumber \]

\(HN/N = \phi(H) \cong H / H \cap N\text{.}\)

Teorema\(11.13\). Correspondence Theorem

Dejar\(N\) ser un subgrupo normal de un grupo\(G\text{.}\) Entonces\(H \mapsto H/N\) es una correspondencia uno a uno entre el conjunto de subgrupos\(H\) de\(G\) contención\(N\) y el conjunto de subgrupos de \(G/N\text{.}\)Además, los subgrupos normales de\(G\) contenido\(N\) corresponden a subgrupos normales de\(G/N\text{.}\)

Prueba

Dejar\(H\) ser un subgrupo de\(G\) contener\(N\text{.}\) Ya que\(N\) es normal en\(H\text{,}\)\(H/N\) es un grupo de factores. Dejar\(aN\) y\(bN\) ser elementos de\(H/N\text{.}\) Entonces\((aN)( b^{-1} N )= ab^{-1}N \in H/N\text{;}\) por lo tanto,\(H/N\) es un subgrupo de\(G/N\text{.}\)

Dejar\(S\) ser un subgrupo de\(G/N\text{.}\) Este subgrupo es un conjunto de coconjuntos de\(N\text{.}\) Si\(H= \{ g \in G : gN \in S \}\text{,}\) entonces para\(h_1, h_2 \in H\text{,}\) nosotros tenemos eso\((h_1 N)( h_2 N )= h_1 h_2 N \in S\) y\(h_1^{-1} N \in S\text{.}\) Por lo tanto,\(H\) debe ser un subgrupo de\(G\text{.}\) Claramente,\(H\) contiene\(N\text{.}\) Por lo tanto, en\(S = H / N\text{.}\) consecuencia, el mapa\(H \mapsto H/N\) está en.

Supongamos que\(H_1\) y\(H_2\) son subgrupos de\(G\) contener\(N\) tal que\(H_1/N = H_2/N\text{.}\) si\(h_1 \in H_1\text{,}\) entonces\(h_1 N \in H_1/N\text{.}\) Por lo tanto,\(h_1 N = h_2 N \subset H_2\) para algunos\(h_2\) en\(H_2\text{.}\) Sin embargo, ya que\(N\) está contenido en\(H_2\text{,}\) sabemos que\(h_1 \in H_2\) o\(H_1 \subset H_2\text{.}\) De manera similar, \(H_2 \subset H_1\text{.}\)Ya que\(H_1 = H_2\text{,}\) el mapa\(H \mapsto H/N\) es uno a uno.

Supongamos que\(H\) es normal en\(G\) y\(N\) es un subgrupo de\(H\text{.}\) Entonces es fácil verificar que el mapa\(G/N \rightarrow G/H\) definido por\(gN \mapsto gH\) es un homomorfismo. El núcleo de este homomorfismo es el\(H/N\text{,}\) que demuestra que\(H/N\) es normal en\(G/N\text{.}\)

Por el contrario, supongamos que eso\(H/N\) es normal en\(G/N\text{.}\) El homomorfismo dado por

\[ G \rightarrow G/N \rightarrow \frac{G/N}{H/N} \nonumber \]

tiene kernel\(H\text{.}\) Por lo tanto,\(H\) debe ser normal en\(G\text{.}\)

Observe que en el transcurso de la prueba del Teorema\(11.13\), también hemos probado el siguiente teorema.

Teorema\ (11.14\. Teorema del Tercer Isomorfismo

Dejar\(G\) ser un grupo y\(N\) y\(H\) ser subgrupos normales de\(G\) con\(N \subset H\text{.}\) Entonces

\[ G/H \cong \frac{G/N}{H/N}\text{.} \nonumber \]

Ejemplo\(11.15\)

Por el Tercer Teorema del Isomorfismo,

\[ {\mathbb Z} / m {\mathbb Z} \cong ({\mathbb Z}/ mn {\mathbb Z})/ (m {\mathbb Z}/ mn {\mathbb Z})\text{.} \nonumber \]

Solución

Desde\(| {\mathbb Z} / mn {\mathbb Z} | = mn\) y\(|{\mathbb Z} / m{\mathbb Z}| = m\text{,}\) tenemos\(| m {\mathbb Z} / mn {\mathbb Z}| = n\text{.}\)