23.2: El Teorema Fundamental

El objetivo de esta sección es probar el Teorema Fundamental de la Teoría Galois. Este teorema explica la conexión entre los subgrupos de\(G(E/F)\) y los campos intermedios entre\(E\) y\(F\).

Proposición\(23.14\).

Dejar\(\{\sigma_i : i \in I \}\) ser una colección de automorfismos de un campo\(F\). Entonces

\[ F_{\{\sigma_i \}} = \{ a \in F : \sigma_i(a) = a \text{ for all } \sigma_i \} \nonumber \]

es un subcampo de\(F\).

Prueba

Dejar\(\sigma_i(a) = a\) y\(\sigma_i(b)=b\). Entonces

\[ \sigma_i(a \pm b) = \sigma_i(a) \pm \sigma_i(b) = a \pm b \nonumber \]

y

\[ \sigma_i(a b) = \sigma_i(a) \sigma_i(b) = a b\text{.} \nonumber \]

Si\(a \neq 0\text{,}\) entonces\(\sigma_i(a^{-1}) = [\sigma_i(a)]^{-1} = a^{-1}\). Por último,\(\sigma_i(0) = 0\) y\(\sigma_i(1)=1\) ya\(\sigma_i\) es un automorfismo.

Corolario\(23.15\).

Dejar\(F\) ser un campo y dejar\(G\) ser un subgrupo de\(\aut(F)\). Entonces

\[ F_G = \{ \alpha \in F : \sigma( \alpha ) = \alpha \text{ for all } \sigma \in G \} \nonumber \]

es un subcampo de\(F\).

El subcampo\(F_{ \{\sigma_i \} }\) de\(F\) se llama el campo fijo de\(\{ \sigma_i \}\). El campo fijado por un subgrupo\(G\) de\(\aut(F)\) será denotado por\(F_G\).

Ejemplo\(23.16\).

Déjese\(\sigma : {\mathbb Q}(\sqrt{3}, \sqrt{5}\, ) \rightarrow {\mathbb Q}(\sqrt{3}, \sqrt{5}\, )\) ser el automorfismo\(\sqrt{3}\) al que se mapea\(-\sqrt{3}\).

Solución

Entonces\({\mathbb Q}( \sqrt{5}\, )\) es el subcampo de\({\mathbb Q}(\sqrt{3}, \sqrt{5}\, )\) izquierda fijado por\(\sigma\).

Proposición\(23.17\).

Dejar\(E\) ser un campo\(F\) de división sobre un polinomio separable. Entonces\(E_{G(E/F)} = F\).

Prueba

Vamos\(G = G(E/F)\). Claramente,\(F \subset E_G \subset E\). Además,\(E\) debe ser un campo de división de\(E_G\) y\(G(E/F) = G(E/E_G)\). Por teorema\(23.7\),

\[ |G| = [E: E_G] =[ E:F]\text{.} \nonumber \]

Por lo tanto,\([E_G : F ] =1\). En consecuencia,\(E_G = F\).

Un gran número de matemáticos aprendieron por primera vez la teoría de Galois a partir de la monografía de Emil Artin sobre el tema [1]. La prueba muy inteligente del siguiente lema se debe a Artin.

Lema\(23.18\).

Dejar\(G\) ser un grupo finito de automorfismos de\(E\) y dejar\(F = E_G\). Entonces\([E:F] \leq |G|\).

Prueba

Vamos\(|G| = n\). Debemos demostrar que cualquier conjunto de\(n + 1\) elementos\(\alpha_1, \ldots, \alpha_{n + 1}\) en\(E\) es linealmente dependiente sobre\(F\text{;}\) esto es, necesitamos encontrar elementos\(a_i \in F\text{,}\) no todos cero, tal que

\[ a_1 \alpha_1 + a_2 \alpha_2 + \cdots + a_{n + 1} \alpha_{n + 1} = 0\text{.} \nonumber \]

Supongamos que\(\sigma_1 = \identity, \sigma_2, \ldots, \sigma_n\) son los automorfismos en\(G\). El sistema homogéneo de ecuaciones lineales

\ begin {alinear*}\ sigma_1 (\ alpha_1) x_1 +\ sigma_1 (\ alpha_2) x_2 +\ cdots +\ sigma_1 (\ alpha_ {n + 1}) x_ {n + 1} & = 0\\\ sigma_2 (\ alpha_1) x_1 +\ sigma_2 (\ alpha_2) x_2 +\ cdots +\ sigma_2 (\ alpha_ {n + 1}) x_ {n + 1} & = 0\\ &\ vdots &\\\ sigma_n (\ alpha_1) x_1 +\ sigma_n (\ alpha_2) x_2 +\ cdots + \ sigma_n (\ alpha_ {n + 1}) x_ {n + 1} & = 0\ end {alinear*}

tiene más incógnitas que ecuaciones. A partir del álgebra lineal sabemos que este sistema tiene una solución no trivial, digamos\(x_i = a_i\) por\(i = 1, 2, \ldots, n + 1\). Como\(\sigma_1\) es la identidad, la primera ecuación se traduce en

\[ a_1 \alpha_1 + a_2 \alpha_2 + \cdots + a_{n + 1} \alpha_{n + 1} = 0\text{.} \nonumber \]

El problema es que algunos de los\(a_i\)'s pueden estar adentro\(E\) pero no en\(F\). Debemos demostrar que esto es imposible.

Supongamos que al menos uno de los\(a_i\)'s está adentro\(E\) pero no en\(F\). Al reorganizar los\(\alpha_i\)'s podemos suponer que\(a_1\) es distinto de cero. Dado que cualquier múltiplo distinto de cero de una solución también es una solución, también podemos suponer que\(a_1 = 1\). De todas las soluciones posibles que se ajusten a esta descripción, elegimos la que tiene el menor número de términos distintos de cero. Nuevamente, reordenando\(\alpha_2, \ldots, \alpha_{n + 1}\) si es necesario, podemos asumir que\(a_2\) está adentro\(E\) pero no en\(F\). Ya que\(F\) es el subcampo de\(E\) que se fija elementwise por\(G\text{,}\) existe un\(\sigma_i\) en\(G\) tal que\(\sigma_i( a_2 ) \neq a_2\). Aplicando\(\sigma_i\) a cada ecuación en el sistema, terminamos con el mismo sistema homogéneo, ya que\(G\) es un grupo. Por lo tanto,\(x_1 = \sigma_i(a_1) = 1\text{,}\)\(x_2 = \sigma_i(a_2)\text{,}\)\(\ldots\text{,}\)\(x_{n + 1} = \sigma_i(a_{n+1} )\) es también una solución del sistema original. Sabemos que una combinación lineal de dos soluciones de un sistema homogéneo es también una solución; en consecuencia,

\ begin {align*} x_1 & = 1 -1 = 0\\ x_2 & = a_2 -\ sigma_i (a_2)\\ &\ vdots &\\ x_ {n + 1} & = a_ {n + 1} -\ sigma_i (a_ {n + 1})\ end {align*}

debe ser otra solución del sistema. Esta es una solución no trivial porque\(\sigma_i( a_2 ) \neq a_2\text{,}\) y tiene menos entradas distintas de cero que nuestra solución original. Esto es una contradicción, ya que se suponía que el número de soluciones distintas de cero a nuestra solución original era mínimo. Por lo tanto, podemos concluir eso\(a_1, \ldots, a_{n + 1} \in F\).

Let\(E\) Ser una extensión algebraica de\(F\). Si cada polinomio irreducible adentro\(F[x]\) con una raíz adentro\(E\) tiene todas sus raíces en\(E\text{,}\) entonces\(E\) se llama una extensión normal de\(F\text{;}\) eso es, cada polinomio irreducible en\(F[x]\) contener una raíz adentro\(E\) es el producto de lineal factores en\(E[x]\).

Teorema\(23.19\).

Let\(E\) Ser una extensión de campo de\(F\). Entonces las siguientes declaraciones son equivalentes.

1. \(E\)es una extensión finita, normal y separable de\(F\).
2. \(E\)es un campo\(F\) de división sobre un polinomio separable.
3. \(F = E_G\)para algún grupo finito\(G\) de automorfismos de\(E\).

Prueba

(1)\(\Rightarrow\) (2). Dejar\(E\) ser una extensión finita, normal, separable de\(F\). Por el Teorema del Elemento Primitivo, podemos encontrar un\(\alpha\) en\(E\) tal que\(E = F(\alpha)\). Dejado\(f(x)\) ser el polinomio mínimo de\(\alpha\) más\(F\). El campo\(E\) debe contener todas las raíces de\(f(x)\) ya que es una extensión normal\(F\text{;}\) por lo tanto,\(E\) es un campo de división para\(f(x)\).

(2)\(\Rightarrow\) (3). Dejado\(E\) ser el campo\(F\) de división sobre de un polinomio separable. Por Proposición 23.17,\(E_{G(E/F)} = F\). Ya que se\(| G(E/F)| = [E:F]\text{,}\) trata de un grupo finito.

(3)\(\Rightarrow\) (1). Vamos\(F = E_G\) por algún grupo finito de automorfismos\(G\) de\(E\). Dado que\([E:F] \leq |G|\text{,}\)\(E\) es una extensión finita de\(F\). Demostrar que\(E\) es una extensión finita y normal de\(F\text{,}\) let\(f(x) \in F[x]\) be un polinomio monico irreducible que tiene una raíz\(\alpha\) en\(E\). Debemos demostrar que\(f(x)\) es producto de distintos factores lineales en\(E[x]\). Por la Proposición 23.5, los automorfismos en\(G\) permutan las raíces de\(f(x)\) mentir en\(E\). De ahí que si dejamos\(G\) actuar sobre\(\alpha\text{,}\) nosotros podemos obtener raíces distintas\(\alpha_1 = \alpha, \alpha_2, \ldots, \alpha_n\) en\(E\). Vamos\(g(x) = \prod_{i = 1}^{n} (x -\alpha_i)\). Entonces\(g(x)\) es separable una\(F\) y otra vez\(g( \alpha ) = 0\). Cualquier automorfismo\(\sigma\) en\(G\) permuta los factores de\(g(x)\) ya que permuta estas raíces; de ahí, cuando\(\sigma\) actúa sobre\(g(x)\text{,}\) ella se deben fijar los coeficientes de\(g(x)\). Por lo tanto, los coeficientes de\(g(x)\) deben estar en\(F\). Dado que\(\deg g(x) \leq \deg f(x)\) y\(f(x)\) es el polinomio mínimo de\(\alpha\text{,}\)\(f(x) = g(x)\).

Corolario\(23.20\).

\(K\)Sea una extensión de campo de\(F\) tal que\(F = K_G\) para algún grupo finito de automorfismos\(G\) de\(K\). Entonces\(G = G(K/F)\).

Prueba

Dado que\(F = K_G\text{,}\)\(G\) es un subgrupo de\(G(K/F)\). Por lo tanto,\[ [K : F ] \leq |G| \leq |G(K/F)| = [K:F]\text{.} \nonumber \]

De ello se deduce que\(G = G(K/F)\text{,}\) ya que deben tener el mismo orden.

Antes de determinar la correspondencia exacta entre extensiones de campo y automorfismos de campos, volvamos a un ejemplo familiar.

Ejemplo\(23.21\)

En Ejemplo\(23.4\) examinamos los automorfismos de\({\mathbb Q}( \sqrt{3}, \sqrt{5}\, )\) fijación\({\mathbb Q}\).

Solución

La figura\(23.22\) compara la celosía de extensiones de campo de\({\mathbb Q}\) con la celosía de subgrupos de\(G( {\mathbb Q}( \sqrt{3}, \sqrt{5}\, ) /{\mathbb Q})\). El Teorema Fundamental de la Teoría Galois nos dice cuál es la relación entre las dos celosías.

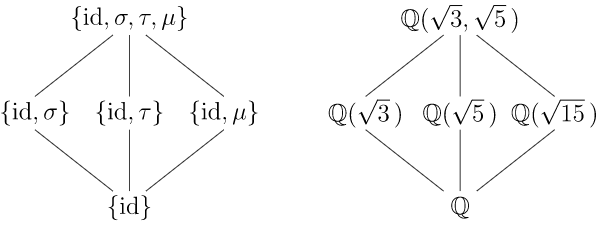
Figura 23.22:\(G({\mathbb Q( \sqrt{3}, \sqrt{5}\, ) / {\mathbb Q})}\)

Ahora estamos listos para afirmar y probar el Teorema Fundamental de la Teoría Galois.

Teorema\(23.23\). Fundamental Theorem of Galois Theory.

Dejar\(F\) ser un campo finito o un campo de cero característico. Si\(E\) es una extensión normal finita de\(F\) con grupo Galois\(G(E/F)\text{,}\) entonces las siguientes afirmaciones son verdaderas.

1. El mapa\(K \mapsto G(E/K)\) es una biyección de subcampos\(K\) de\(E\) contención\(F\) con los subgrupos de\(G(E/F)\).
2. Si\(F \subset K \subset E\text{,}\) entonces
   \[ [E:K] = |G(E/K)| \text{ and } [K:F] = [G(E/F):G(E/K)]\text{.} \nonumber \]
3. \(F \subset K \subset L \subset E\)si y sólo si\(\{ \identity \} \subset G(E/L) \subset G(E/K) \subset G(E/F)\).
4. \(K\)es una extensión normal de\(F\) si y sólo si\(G(E/K)\) es un subgrupo normal de\(G( E/F)\). En este caso
   \[ G(K/F) \cong G(E/F) / G( E/K )\text{.} \nonumber \]

Prueba

(1) Supongamos que\(G(E/K) = G(E/L) = G\). Ambos\(K\) y\(L\) son campos fijos de\(G\text{;}\) ahí,\(K=L\) y el mapa definido por\(K \mapsto G(E/K)\) es uno a uno. Para mostrar que el mapa está en, deja\(G\) ser un subgrupo de\(G(E/F)\) y\(K\) ser el campo fijado por\(G\). Entonces en\(F \subset K \subset E\text{;}\) consecuencia,\(E\) es una extensión normal de\(K\). Así,\(G(E/K) = G\) y el mapa\(K \mapsto G(E/K)\) es una biyección.

(2) Por Teorema Teorema 23.7,\(|G(E/K)| = [E:K]\text{;}\) por lo tanto,

\[ |G(E/F)| = [G(E/F):G(E/K)] \cdot |G(E/K)| = [E:F] = [E:K][K:F]\text{.} \nonumber \]

Por lo tanto,\([K:F] = [G(E/F):G(E/K)]\).

El enunciado (3) se ilustra en la Figura 23.24. Dejamos como ejercicio el comprobante de esta propiedad.

(4) Esta parte toma un poco más de trabajo. Dejar\(K\) ser una extensión normal de\(F\). Si\(\sigma\) está adentro\(G(E/F)\) y\(\tau\) está\(G(E/K)\text{,}\) adentro necesitamos demostrar que\(\sigma^{-1} \tau \sigma\) está en\(G(E/K)\text{;}\) eso es, necesitamos mostrarlo\(\sigma^{-1} \tau \sigma( \alpha) = \alpha\) para todos\(\alpha \in K\). Supongamos que ese\(f(x)\) es el polinomio mínimo de\(\alpha\) over\(F\). Entonces también\(\sigma( \alpha )\) es una raíz de\(f(x)\) mentir\(K\text{,}\) ya que\(K\) es una extensión normal de\(F\). De ahí,\(\tau( \sigma( \alpha )) = \sigma( \alpha )\) o\(\sigma^{-1} \tau \sigma( \alpha) = \alpha\).

Por el contrario, dejar\(G(E/K)\) ser un subgrupo normal de\(G(E/F)\). Tenemos que demostrarlo\(F = K_{G(K/F)}\). Vamos\(\tau \in G(E/K)\). Por todos\(\sigma \in G(E/F)\) existe\(\overline{\tau} \in G(E/K)\) tal que\(\tau \sigma = \sigma \overline{\tau}\). En consecuencia, para todos\(\alpha \in K\)

\[ \tau( \sigma( \alpha ) ) = \sigma( \overline{\tau}( \alpha ) ) = \sigma( \alpha ); \nonumber \]

por lo tanto,\(\sigma( \alpha )\) debe estar en el campo fijo de\(G(E/K)\). \(\overline{\sigma}\)Sea la restricción de\(\sigma\) a\(K\). Entonces\(\overline{\sigma}\) es un automorfismo de\(K\) fijación\(F\text{,}\) ya que\(\sigma( \alpha ) \in K\) para todos de\(\alpha \in K\text{;}\) ahí,\(\overline{\sigma} \in G(K/F)\). A continuación, mostraremos que el campo fijo de\(G(K/F)\) es\(F\). Dejar\(\beta\) ser un elemento en\(K\) que se fija por todos los automorfismos en\(G(K/F)\). En particular,\(\overline{\sigma}(\beta) = \beta\) para todos\(\sigma \in G(E/F)\). Por lo tanto,\(\beta\) pertenece al campo fijo\(F\) de\(G(E/F)\).

Por último, debemos demostrar que cuando\(K\) es una extensión normal de\(F\text{,}\)

\[ G(K/F) \cong G(E/F) / G(E/K)\text{.} \nonumber \]

Para\(\sigma \in G(E/F)\text{,}\) dejar\(\sigma_K\) ser el automorfismo de\(K\) obtenido restringiendo\(\sigma\) a\(K\). Ya que\(K\) es una extensión normal, el argumento del párrafo anterior lo demuestra\(\sigma_K \in G( K/F)\). En consecuencia, tenemos un mapa\(\phi:G(E/F) \rightarrow G(K/F)\) definido por\(\sigma \mapsto \sigma_K\). Este mapa es un homomorfismo grupal desde

\[ \phi( \sigma \tau ) = (\sigma \tau)_K = \sigma_K \tau_K = \phi( \sigma) \phi( \tau )\text{.} \nonumber \]

El núcleo de\(\phi\) es\(G(E/K)\). Por (2),

\[ |G(E/F)| / |G(E/K)| = [K:F] = |G(K/F)|\text{.} \nonumber \]

De ahí que la imagen de\(\phi\) es\(G(K/F)\) y\(\phi\) está sobre. Aplicando el Teorema del Primer Isomorfismo, tenemos

\[ G(K/F) \cong G(E/F) / G( E/K )\text{.} \nonumber \]

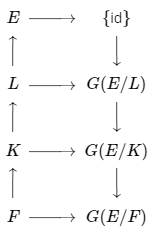
Figura 23.24: Subgrupos\(G(E/F)\) y subcampos de\(E\)

Ejemplo\(23.23\).

En este ejemplo ilustraremos el Teorema Fundamental de la Teoría Galois determinando la red de subgrupos del grupo Galois de\(f(x) = x^4 - 2\). Compararemos esta celosía con la celosía de extensiones de campo de las\({\mathbb Q}\) que están contenidas en el campo de división de\(x^4-2\). El campo de división de\(f(x)\) es\({\mathbb Q}( \sqrt[4]{2}, i )\). Para ver esto, observe que\(f(x)\) factores como de\((x^2 + \sqrt{2}\, )(x^2 - \sqrt{2}\, )\text{;}\) ahí, las raíces de\(f(x)\) son\(\pm \sqrt[4]{2}\) y\(\pm \sqrt[4]{2}\, i\).

Solución

Primero colindamos con la raíz\(\sqrt[4]{2}\) a\({\mathbb Q}\) y luego colindamos con la raíz\(i\) de\(x^2 + 1\) a\({\mathbb Q}(\sqrt[4]{2}\, )\). El campo de división de\(f(x)\) es entonces\({\mathbb Q}(\sqrt[4]{2}\, )(i) = {\mathbb Q}( \sqrt[4]{2}, i )\).

Ya que\([ {\mathbb Q}( \sqrt[4]{2}\, ) : {\mathbb Q}] = 4\) y no\(i\) está en\({\mathbb Q}( \sqrt[4]{2}\, )\text{,}\) ello debe ser el caso que\([ {\mathbb Q}( \sqrt[4]{2}, i ): {\mathbb Q}(\sqrt[4]{2}\, )] = 2\). De ahí,\([ {\mathbb Q}( \sqrt[4]{2}, i ):{\mathbb Q}] = 8\). El conjunto

\[ \{ 1, \sqrt[4]{2}, (\sqrt[4]{2}\, )^2, (\sqrt[4]{2}\, )^3, i, i \sqrt[4]{2}, i (\sqrt[4]{2}\, )^2, i(\sqrt[4]{2}\, )^3 \} \nonumber \]

es una base de\({\mathbb Q}( \sqrt[4]{2}, i )\) más\({\mathbb Q}\). La celosía de las extensiones de campo\({\mathbb Q}\) contenidas en\({\mathbb Q}( \sqrt[4]{2}, i)\) se ilustra en la Figura\(23.26\) (a).

El grupo Galois\(G\) de\(f(x)\) debe ser de orden\(8\). \(\sigma\)Sea el automorfismo definido por\(\sigma( \sqrt[4]{2}\, ) = i \sqrt[4]{2}\) y\(\sigma( i ) = i\text{,}\) y\(\tau\) sea el automorfismo definido por conjugación compleja; es decir,\(\tau(i ) = -i\). Entonces\(G\) tiene un elemento de orden\(4\) y un elemento de orden\(2\). Es fácil verificar por cómputo directo que los elementos de\(G\) son\(\{ \identity, \sigma, \sigma^2, \sigma^3, \tau, \sigma \tau, \sigma^2 \tau, \sigma^3 \tau \}\) y que las relaciones\(\tau^2 = \identity\text{,}\)\(\sigma^4 = \identity\text{,}\) y\(\tau \sigma \tau = \sigma^{-1}\) están satisfechas; por lo tanto,\(G\) deben ser isomórficos a\(D_4\). La red de subgrupos de\(G\) se ilustra en la Figura\(23.26\) (b).

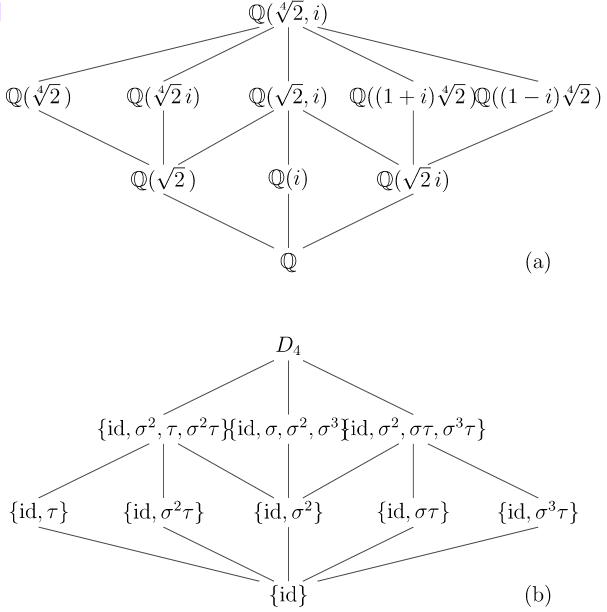
Figura 23.26: Grupo Galois de\(x^4-2\)

Nota Histórica

Las soluciones para las ecuaciones cúbicas y cuárticas fueron descubiertas en los años 1500. Los intentos de encontrar soluciones para las ecuaciones quinticas desconcertaron a algunos de los mejores matemáticos de la historia. En 1798, P. Ruffini presentó un trabajo que afirmaba que no se pudo encontrar tal solución; sin embargo, el trabajo no fue bien recibido. En 1826, Niels Henrik Abel (1802—1829) finalmente ofreció la primera prueba correcta de que los quínticos no siempre son solucionables por los radicales.

Abel inspiró la obra de Évariste Galois. Nacido en 1811, Galois comenzó a mostrar extraordinario talento matemático a la edad de 14 años. Solicitó ingreso a la École Polytechnique varias veces; sin embargo, tuvo grandes dificultades para cumplir con los requisitos formales de ingreso, y los examinadores no reconocieron su genio matemático. Finalmente fue aceptado en la École Normale en 1829.

Galois trabajó para desarrollar una teoría de la solvabilidad para polinomios. En 1829, a la edad de 17 años, Galois presentó dos trabajos sobre la solución de ecuaciones algebraicas a la Académie des Sciences de Paris. Estos papeles fueron enviados a Cauchy, quien posteriormente los perdió. Un tercer trabajo fue enviado a Fourier, quien murió antes de que pudiera leerlo. Se presentó otro trabajo, pero no se publicó hasta 1846.

Las simpatías democráticas de Galois lo llevaron a la Revolución de 1830. Fue expulsado de la escuela y enviado a prisión por su parte en la agitación. Después de su liberación en 1832, fue arrastrado a un duelo posiblemente por una historia de amor. Seguro de que lo matarían, pasó la tarde antes de su muerte delineando su trabajo y sus ideas básicas para la investigación en una larga carta a su amigo Chevalier. De hecho, estaba muerto al día siguiente, a los 20 años.