23.1: Automorfismos de Campo

Nuestra primera tarea es establecer un vínculo entre la teoría de grupos y la teoría de campo mediante el examen de automorfismos de campos.

Proposición\(23.1\).

El conjunto de todos los automorfismos de un campo\(F\) es un grupo bajo composición de funciones.

Prueba

Si\(\sigma\) y\(\tau\) son automorfismos de\(F\text{,}\) entonces así son\(\sigma \tau\) y\(\sigma^{-1}\text{.}\) La identidad es sin duda un automorfismo; de ahí que el conjunto de todos los automorfismos de un campo\(F\) es efectivamente un grupo.

Proposición\(23.2\).

Dejar\(E\) ser una extensión de campo de\(F\text{.}\) Entonces el conjunto de todos los automorfismos de\(E\) ese arreglo\(F\) elementwise es un grupo; es decir, el conjunto de todos los automorfismos\(\sigma : E \rightarrow E\) tal que\(\sigma( \alpha ) = \alpha\) para todos\(\alpha \in F\) es un grupo.

Prueba

Solo necesitamos demostrar que el conjunto de automorfismos de\(E\) ese arreglo\(F\) elementwise es un subgrupo del grupo de todos los automorfismos de\(E\text{.}\) Let\(\sigma\) y\(\tau\) ser dos automorfismos de\(E\) tal que\(\sigma( \alpha ) = \alpha\) y\(\tau( \alpha ) = \alpha\) para todos\(\alpha \in F\text{.}\) Entonces\(\sigma \tau( \alpha ) = \sigma( \alpha) = \alpha\) y \(\sigma^{-1}( \alpha ) = \alpha\text{.}\)Dado que la identidad fija cada elemento\(E\text{,}\) del conjunto de automorfismos de\(E\) que dejan elementos de\(F\) fijo es un subgrupo de todo el grupo de automorfismos de\(E\text{.}\)

Dejar\(E\) ser una extensión de campo de\(F\text{.}\) Vamos a denotar el grupo completo de automorfismos de\(E\) por\(\aut(E)\text{.}\) Definimos el grupo Galois de\(E\) over\(F\) para ser el grupo de automorfismos de\(E\) ese arreglo\(F\) elementwise; es decir,

\[ G(E/F) = \{ \sigma \in \aut(E) : \sigma(\alpha) = \alpha \text{ for all } \alpha \in F \}\text{.} \nonumber \]

Si\(f(x)\) es un polinomio en\(F[x]\) y\(E\) es el campo de división de\(f(x)\) más\(F\text{,}\) entonces definimos el grupo Galois de\(f(x)\) ser\(G(E/F)\text{.}\)

Ejemplo\(23.3\).

La conjugación compleja, definida por\(\sigma : a + bi \mapsto a - bi\text{,}\) es un automorfismo de los números complejos. Desde

Solución

\[ \sigma(a) = \sigma(a + 0i) = a - 0i = a\text{,} \nonumber \]

el automorfismo definido por conjugación compleja debe estar en\(G( {\mathbb C} / {\mathbb R} )\text{.}\)

Ejemplo\(23.4\).

Considerar los campos\({\mathbb Q} \subset {\mathbb Q}(\sqrt{5}\, ) \subset {\mathbb Q}( \sqrt{3}, \sqrt{5}\, )\text{.}\)

Solución

Entonces para\(a, b \in {\mathbb Q}( \sqrt{5}\, )\text{,}\)

\[ \sigma( a + b \sqrt{3}\, ) = a - b \sqrt{3} \nonumber \]

es un automorfismo de\({\mathbb Q}(\sqrt{3}, \sqrt{5}\, )\) dejar\({\mathbb Q}( \sqrt{5}\, )\) fijo. Del mismo modo,

\[ \tau( a + b \sqrt{5}\, ) = a - b \sqrt{5} \nonumber \]

es un automorfismo de\({\mathbb Q}(\sqrt{3}, \sqrt{5}\, )\) dejar\({\mathbb Q}( \sqrt{3}\, )\) fijo. El automorfismo\(\mu = \sigma \tau\) mueve ambos\(\sqrt{3}\) y pronto quedará\(\sqrt{5}\text{.}\) claro que\(\{ \identity, \sigma, \tau, \mu \}\) es el grupo Galois de\({\mathbb Q}(\sqrt{3}, \sqrt{5}\, )\) más\({\mathbb Q}\text{.}\) La siguiente tabla muestra que este grupo es isomórfico para\({\mathbb Z}_2 \times {\mathbb Z}_2\text{.}\)

\[ \begin{array}{c|cccc} & \identity & \sigma & \tau & \mu \\ \hline \identity & \identity & \sigma & \tau & \mu \\ \sigma & \sigma & \identity & \mu & \tau \\ \tau & \tau & \mu & \identity & \sigma \\ \mu & \mu & \tau & \sigma & \identity \end{array} \nonumber \]

También podemos considerar el campo\({\mathbb Q}( \sqrt{3}, \sqrt{5}\, )\) como un espacio vectorial sobre\({\mathbb Q}\) eso tiene base\(\{ 1, \sqrt{3}, \sqrt{5}, \sqrt{15}\, \}\text{.}\) No es casualidad que\(|G( {\mathbb Q}( \sqrt{3}, \sqrt{5}\, ) /{\mathbb Q})| = [{\mathbb Q}(\sqrt{3}, \sqrt{5}\, ):{\mathbb Q})] = 4\text{.}\)

Proposición\(23.5\).

Dejar\(E\) ser una extensión de campo de\(F\) y\(f(x)\) ser un polinomio en\(F[x]\text{.}\) Entonces cualquier automorfismo en\(G(E/F)\) define una permutación de las raíces de\(f(x)\) que se encuentran en\(E\text{.}\)

Prueba

Let

\[ f(x) = a_0 + a_1 x + a_2 x^2 + \cdots + a_n x^n \nonumber \]

y supongamos que\(\alpha \in E\) es un cero de\(f(x)\text{.}\) Entonces para\(\sigma \in G(E/F)\text{,}\)

\ begin {align*} 0 & =\ sigma (0)\\ & =\ sigma (f (\ alpha))\\ & =\ sigma (a_0 + a_1\ alpha + a_2\ alpha^2 +\ cdots + a_n\ alpha^n)\\ & = a_0 + a_1\ sigma (\ alpha) + a_2 [\ sigma (\ alpha)] ^2 +\ cdots + n [\ sigma (\ alfa)] ^n;\ final {alinear*}

por lo tanto, también\(\sigma( \alpha )\) es un cero de\(f(x)\text{.}\)

Dejar\(E\) ser una extensión algebraica de un campo\(F\text{.}\) Dos elementos\(\alpha, \beta \in E\) se conjugan sobre\(F\) si tienen el mismo polinomio mínimo. Por ejemplo, en\({\mathbb Q}( \sqrt{2}\, )\) el campo los elementos\(\sqrt{2}\) y\(-\sqrt{2}\) son conjugados\({\mathbb Q}\) ya que ambos son raíces del polinomio irreducible\(x^2 - 2\text{.}\)

Existe una conversa de la última proposición. La prueba sigue directamente de Lemma\(21.32\).

Proposición\(23.6\).

Si\(\alpha\) y\(\beta\) son conjugados por\(F\text{,}\) ahí existe un isomorfismo\(\sigma : F( \alpha ) \rightarrow F( \beta )\) tal que\(\sigma\) es la identidad cuando se restringe a\(F\text{.}\)

Teorema\(23.7\).

Dejar\(f(x)\) ser un polinomio en\(F[x]\) y supongamos que ese\(E\) es el campo de división para\(f(x)\) más\(F\text{.}\) Si no\(f(x)\) tiene raíces repetidas, entonces

\[ |G(E/F)| = [E:F]\text{.} \nonumber \]

Prueba

Usaremos la inducción matemática en\([E:F]\text{.}\) Si\([E:F] = 1\text{,}\) entonces\(E = F\) y no hay nada que mostrar. Si\([E:F] \gt 1\text{,}\) vamos\(f(x) = p(x)q(x)\text{,}\) donde\(p(x)\) es irreducible de grado\(d\text{.}\) Podemos suponer que de\(d \gt 1\text{;}\) otra manera, se\(f(x)\) divide\(F\) y\([E:F] = 1\text{.}\) deja\(\alpha\) ser una raíz de\(p(x)\text{.}\) Si\(\phi: F(\alpha) \to E\) es algún homomorfismo inyectivo, entonces\(\phi( \alpha) = \beta\) es una raíz de \(p(x)\text{,}\)y\(\phi: F(\alpha) \to F(\beta)\) es un automorfismo de campo. Ya que no\(f(x)\) tiene raíces repetidas,\(p(x)\) tiene exactamente\(d\) raíces\(\beta \in E\text{.}\) Por Proposición\(23.5\), hay exactamente\(d\) isomorfismos\(\phi: F(\alpha) \to F(\beta_i)\) que fijan\(F\text{,}\) uno por cada raíz\(\beta_1, \ldots, \beta_d\) de\(p(x)\) (ver Figura\(23.8\)).

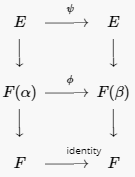
\(Figure \text { } 23.8.\)

Dado que\(E\) es un campo de división de\(f(x)\) sobre también\(F\text{,}\) es un campo de división sobre\(F(\alpha)\text{.}\) Similarmente,\(E\) es un campo de división de\(f(x)\) más\(F(\beta)\text{.}\) Desde la\([E: F(\alpha)] = [E:F]/d\text{,}\) inducción muestra que cada uno de los\(d\) isomorfismos\(\phi\) tiene exactamente\([E:F]/d\) extensiones,\(\psi : E \to E\text{,}\) y hemos construido\([E:F]\) isomorfismos que arreglan\(F\text{.}\) Finalmente, supongamos que\(\sigma\) es alguna fijación de automorfismo\(F\text{.}\) Entonces\(\sigma\) restringido a\(F(\alpha)\) es\(\phi\) para algunos\(\phi: F(\alpha) \to F(\beta)\text{.}\)

Corolario\(23.9\).

Dejar\(F\) ser un campo finito con una extensión finita\(E\) tal que\([E:F]=k\text{.}\) Entonces\(G(E/F)\) es cíclico de orden\(k\text{.}\)

Prueba

\(p\)Sea la característica de\(E\) y\(F\) y asuma que las órdenes de\(E\) y\(F\) son\(p^m\) y\(p^n\text{,}\) respectivamente. Entonces también\(nk = m\text{.}\) podemos suponer que\(E\) es el campo de división de\(x^{p^m} - x\) más de un subcampo de orden\(p\text{.}\) Por lo tanto, también\(E\) debe ser el campo de división de\(x^{p^m} - x\) sobre\(F\text{.}\) Aplicando Teorema\(23.7\), encontramos que\(|G(E/F)| = k\text{.}\)

Para probar que\(G(E/F)\) es cíclico, debemos encontrar un generador para\(G(E/F)\text{.}\) Let\(\sigma : E \rightarrow E\) ser definido por\(\sigma(\alpha) = \alpha^{p^n}\text{.}\) Afirmamos que\(\sigma\) es el elemento en el\(G(E/F)\) que estamos buscando. Primero tenemos que demostrar que\(\sigma\) está en\(\aut(E)\text{.}\) Si\(\alpha\) y\(\beta\) estamos en\(E\text{,}\)

\[ \sigma(\alpha + \beta) = (\alpha + \beta)^{p^n} = \alpha^{p^n} + \beta^{p^n} = \sigma(\alpha) + \sigma(\beta) \nonumber \]

por Lemma\(22.3\). Además, es fácil demostrar que\(\sigma(\alpha \beta) = \sigma( \alpha ) \sigma( \beta )\text{.}\) Dado que\(\sigma\) es un homomorfismo de campos distinto de cero, debe ser inyectivo. También debe estar sobre, ya que\(E\) es un campo finito. Sabemos que\(\sigma\) debe estar en\(G(E/F)\text{,}\) ya que\(F\) es el campo de división de\(x^{p^n} - x\) sobre el campo base de orden\(p\text{.}\) Esto significa que\(\sigma\) deja a cada elemento en\(F\) fijo. Por último, debemos demostrar que el orden de\(\sigma\) es\(k\text{.}\) Por Teorema\(23.7\), sabemos que

\[ \sigma^k( \alpha ) = \alpha^{p^{nk}} = \alpha^{p^m} = \alpha \nonumber \]

es la identidad de\(G( E/F)\text{.}\) Sin embargo,\(\sigma^r\) no puede ser la identidad porque de\(1 \leq r \lt k\text{;}\) otra manera,\(x^{p^{nr}} - x\) tendría\(p^m\) raíces, lo cual es imposible.

Ejemplo\(23.10\).

Ahora podemos confirmar que el grupo Galois de\({\mathbb Q}( \sqrt{3}, \sqrt{5}\, )\) más\({\mathbb Q}\) en Ejemplo\(23.4\) es de hecho isomórfico a\({\mathbb Z}_2 \times {\mathbb Z}_2\text{.}\)

Solución

Ciertamente el grupo\(H = \{ \identity, \sigma, \tau, \mu \}\) es un subgrupo de\(G({\mathbb Q}( \sqrt{3}, \sqrt{5}\, )/{\mathbb Q})\text{;}\) sin embargo,\(H\) debe ser todo\(G({\mathbb Q}( \sqrt{3}, \sqrt{5}\, )/{\mathbb Q})\text{,}\) desde

\[ |H| = [{\mathbb Q}( \sqrt{3}, \sqrt{5}\, ):{\mathbb Q}] = |G({\mathbb Q}( \sqrt{3}, \sqrt{5}\, )/{\mathbb Q})| = 4\text{.} \nonumber \]

Ejemplo\(23.11\).

Vamos a calcular el grupo Galois de

\[ f(x) = x^4 + x^3 + x^2 + x + 1 \nonumber \]

sobre\({\mathbb Q}\text{.}\)

Solución

Sabemos que\(f(x)\) es irreducible por Ejercicio\(17.5.20\) en el Capítulo 17. Además, ya que\((x -1)f(x) = x^5 - 1\text{,}\) podemos usar el Teorema de DemoIVRE para determinar que las raíces de\(f(x)\) son\(\omega^i\text{,}\) dónde\(i = 1, \ldots, 4\) y

\[ \omega = \cos(2 \pi / 5 ) + i \sin(2 \pi / 5 )\text{.} \nonumber \]

De ahí que el campo de división de\(f(x)\) must be\({\mathbb Q}(\omega)\text{.}\) Podemos definir automorfismos\(\sigma_i\) de\({\mathbb Q}(\omega )\) by\(\sigma_i( \omega ) = \omega^i\) for\(i = 1, \ldots, 4\text{.}\) Es fácil comprobar que estos son efectivamente distintos automorfismos en\(G( {\mathbb Q}( \omega) / {\mathbb Q} )\text{.}\) Since

\[ [{\mathbb Q}( \omega) : {\mathbb Q}] = | G( {\mathbb Q}( \omega) / {\mathbb Q})| = 4\text{,} \nonumber \]

los\(\sigma_i\)'s deben ser todos\(G( {\mathbb Q}( \omega) / {\mathbb Q} )\text{.}\) Por lo tanto,\(G({\mathbb Q}( \omega) / {\mathbb Q})\cong {\mathbb Z}_4\) ya que\(\omega\) es un generador para el grupo Galois.

Extensiones separables

Muchos de los resultados que acabamos de demostrar dependen de que un polinomio\(f(x)\) en no\(F[x]\) tiene raíces repetidas en su campo de división. Es evidente que necesitamos saber exactamente cuándo un polinomio faceta en distintos factores lineales en su campo de división. Dejar\(E\) ser el campo de división de un polinomio\(f(x)\) en\(F[x]\text{.}\) Supongamos que\(f(x)\) factores sobre\(E\) como

\[ f(x) = (x - \alpha_1)^{n_1} (x - \alpha_2)^{n_2} \cdots (x - \alpha_r)^{n_r} = \prod_{i = 1}^{r} (x - \alpha_i)^{n_i}\text{.} \nonumber \]

Definimos la multiplicidad de una raíz\(\alpha_i\) de\(f(x)\) ser\(n_i\text{.}\) Una raíz con multiplicidad 1 se llama raíz simple. Recordemos que un polinomio\(f(x) \in F[x]\) de grado\(n\) es separable si tiene raíces\(n\) distintas en su campo de división\(E\text{.}\) Equivalentemente,\(f(x)\) es separable si facciona en distintos factores lineales sobre\(E[x]\text{.}\) una extensión\(E\) de \(F\)es una extensión separable de\(F\) si cada elemento en\(E\) es la raíz de un polinomio separable en\(F[x]\text{.}\) También recuerde que\(f(x)\) es separable si y solo si\(\gcd( f(x), f'(x)) = 1\) (Lema\(22.5\)).

Proposición\(23.12\).

Dejar\(f(x)\) ser un polinomio irreducible sobre\(F\text{.}\) Si la característica de\(F\) es\(0\text{,}\) entonces\(f(x)\) es separable. Si la característica de\(F\) es\(p\) y\(f(x) \neq g(x^p)\) para algunos\(g(x)\) en\(F[x]\text{,}\) entonces también\(f(x)\) es separable.

Prueba

Primero supongamos que\(\chr F = 0\text{.}\) Desde\(\deg f'(x) \lt \deg f(x)\) y\(f(x)\) es irreducible, la única manera\(\gcd( f(x), f'(x)) \neq 1\) es si\(f'(x)\) es el polinomio cero; sin embargo, esto es imposible en un campo de cero característico. Si\(\chr F = p\text{,}\) entonces\(f'(x)\) puede ser el polinomio cero si cada coeficiente de\(f'(x)\) es un múltiplo de\(p\text{.}\) Esto puede suceder solo si tenemos un polinomio de la forma\(f(x) = a_0 + a_1 x^p + a_2 x^{2p} + \cdots + a_n x^{np}\text{.}\)

Ciertamente las extensiones de un campo\(F\) de la forma\(F(\alpha)\) son algunas de las más fáciles de estudiar y entender. Dada una extensión\(E\) de campo de\(F\text{,}\) la pregunta obvia a hacer es cuándo es posible encontrar un elemento\(\alpha \in E\) tal que\(E = F( \alpha )\text{.}\) en este caso,\(\alpha\) se denomina elemento primitivo. Ya sabemos que los elementos primitivos existen para ciertas extensiones. Por ejemplo,

\[ {\mathbb Q}( \sqrt{3}, \sqrt{5}\, ) = {\mathbb Q}( \sqrt{3} + \sqrt{5}\, ) \nonumber \]

y

\[ {\mathbb Q}( \sqrt[3]{5}, \sqrt{5}\, i ) = {\mathbb Q}( \sqrt[6]{5}\, i )\text{.} \nonumber \]

El corolario nos\(22.12\) dice que existe un elemento primitivo para cualquier extensión finita de un campo finito. El siguiente teorema nos dice que a menudo podemos encontrar un elemento primitivo.

Teorema\(23.13\). Primitive Element Theorem.

\(E\)Sea una extensión separable finita de un campo\(F\text{.}\) Entonces existe\(\alpha \in E\) tal que\(E=F( \alpha )\text{.}\)

Prueba

Ya sabemos que no hay problema si\(F\) es un campo finito. Supongamos que\(E\) es una extensión finita de un campo infinito. Demostraremos el resultado para\(F(\alpha, \beta)\text{.}\) El caso general sigue fácilmente cuando usamos la inducción matemática. Dejar\(f(x)\) y\(g(x)\) ser los polinomios mínimos de\(\alpha\) y\(\beta\text{,}\) respectivamente. Que\(K\) sea el campo en el que ambos\(f(x)\) y\(g(x)\) se dividan. Supongamos que\(f(x)\) tiene ceros\(\alpha = \alpha_1, \ldots, \alpha_n\) en\(K\) y\(g(x)\) tiene ceros\(\beta = \beta_1, \ldots, \beta_m\) en\(K\text{.}\) Todos estos ceros tienen multiplicidad\(1\text{,}\) ya que\(E\) es separable sobre\(F\text{.}\) Ya que\(F\) es infinito, podemos encontrar un\(a\) en\(F\) tal que

\[ a \neq \frac{\alpha_i - \alpha}{\beta - \beta_j} \nonumber \]

para todos\(i\) y\(j\) con\(j \neq 1\text{.}\) Por lo tanto,\(a( \beta - \beta_j ) \neq \alpha_i - \alpha\text{.}\) Que\(\gamma = \alpha + a \beta\text{.}\) Entonces

\[ \gamma = \alpha + a \beta \neq \alpha_i + a \beta_j; \nonumber \]

por lo tanto,\(\gamma - a \beta_j \neq \alpha_i\) para todos\(i, j\) con\(j \neq 1\text{.}\) Definir\(h(x) \in F( \gamma )[x]\) por\(h(x) = f( \gamma - ax)\text{.}\) Entonces\(h( \beta ) = f( \alpha ) = 0\text{.}\) Sin embargo,\(h( \beta_j ) \neq 0\) para\(j \neq 1\text{.}\) Por lo tanto,\(h(x)\) y\(g(x)\) tener un solo factor común en\(F( \gamma )[x]\text{;}\) esto es, el polinomio mínimo de\(\beta\) over\(F( \gamma )\) debe ser lineal, ya que \(\beta\)es el único cero común a ambos\(g(x)\) y\(h(x)\text{.}\) Así\(\beta \in F( \gamma )\) y\(\alpha = \gamma - a \beta\) está en\(F( \gamma )\text{.}\) Por lo tanto,\(F( \alpha, \beta ) = F( \gamma )\text{.}\).