23.3: Aplicaciones

Solubilidad por Radicales

A lo largo de esta sección asumiremos que todos los campos tienen cero característico para asegurar que los polinomios irreducibles no tengan múltiples raíces. El objetivo inmediato de esta sección es determinar cuándo se\(f(x)\) pueden calcular las raíces de un polinomio con un número finito de operaciones sobre los coeficientes de\(f(x)\text{.}\) Las operaciones permisibles son suma, resta, multiplicación, división y extracción de\(n\) th raíces. Ciertamente la solución a la ecuación cuadrática,\(a x^2 + b x +c = 0\text{,}\) ilustra este proceso:

\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\text{.} \nonumber \]

La única de estas operaciones que podría exigir un campo más grande es la toma\(n\) de raíces. Nos llevan a la siguiente definición.

Un campo\(E\) de extensión de un campo\(F\) es una extensión por radicales si existe una cadena de subcampos

\[ F = F_0 \subset F_1 \subset F_2 \subset \cdots \subset F_r = E \nonumber \]

tal para\(i = 1, 2, \ldots, r\text{,}\) tenemos\(F_i = F_{i - 1}(\alpha_i)\) y\(\alpha_i^{n_i} \in F_{i-1}\) para algún número entero positivo\(n_i\text{.}\) Un polinomio\(f(x)\) es solucionable por radicales sobre\(F\) si el campo\(K\) de división de\(f(x)\) más\(F\) está contenido en una extensión de\(F\) por radicales . Nuestro objetivo es llegar a criterios que nos indiquen si un polinomio\(f(x)\) es solucionable o no por radicales examinando al grupo Galois\(f(x)\text{.}\)

El polinomio más fácil de resolver por los radicales es uno de la forma\(x^n - a\text{.}\) Como discutimos en el Capítulo 4, las raíces de\(x^n - 1\) se llaman las enésimas raíces de la unidad. Estas raíces son un subgrupo finito del campo de división de\(x^n -1\text{.}\) Por Corolario 22.11, las raíces\(n\) th de la unidad forman un grupo cíclico. Cualquier generador de este grupo se llama una enésima raíz primitiva de unidad.

Ejemplo\(23.27\).

El polinomio\(x^n - 1\) es solucionable por radicales sobre\({\mathbb Q}\text{.}\) Las raíces de este polinomio son\(1, \omega, \omega^2, \ldots, \omega^{n - 1}\text{,}\) donde

Solución

\[ \omega = \cos\left( \frac{2 \pi}{n} \right) + i \sin\left( \frac{2 \pi}{n} \right)\text{.} \nonumber \]

El campo de división de\(x^n - 1\) más\({\mathbb Q}\) es\({\mathbb Q}(\omega)\text{.}\)

Demostraremos que un polinomio es solucionable por radicales si su grupo Galois es solucionable. Recordemos que una serie subnormal de un grupo\(G\) es una secuencia finita de subgrupos

\[ G = H_n \supset H_{n-1} \supset \cdots \supset H_1 \supset H_0 = \{ e \}\text{,} \nonumber \]

donde\(H_i\) es normal en\(H_{i+1}\text{.}\) Un grupo\(G\) es solucionable si tiene una serie subnormal\(\{ H_i \}\) tal que todos los grupos factoriales\(H_{i+1} /H_i\) son abelianos. Por ejemplo, si examinamos la serie\(\{ \identity \} \subset A_3 \subset S_3\text{,}\) vemos que\(S_3\) es solucionable. Por otro lado, no\(S_5\) es solucionable, por Teorema\(10.11\).

Lema\(23.28\).

Dejar\(F\) ser un campo de cero característico y\(E\) ser el campo de división de\(x^n - a\) over\(F\) con\(a \in F\text{.}\) Then\(G(E/F)\) es un grupo solucionable.

Prueba

Las raíces de\(x^n - a\) son\(\sqrt[n]{a}, \omega \sqrt[n]{a}, \ldots, \omega^{n-1} \sqrt[n]{a}\text{,}\) donde\(\omega\) es una primitiva raíz\(n\) th de unidad. Supongamos que\(F\) contiene todas sus raíces\(n\) th de unidad. Si\(\zeta\) es una de las raíces de\(x^n - a\text{,}\) entonces distintas raíces de\(x^n - a\) son\(\zeta, \omega \zeta, \ldots, \omega^{n - 1} \zeta\text{,}\) y\(E = F(\zeta)\text{.}\) Dado que\(G(E/F)\) permuta las raíces\(x^n - a\text{,}\) los elementos en\(G(E/F)\) deben ser determinados por su acción sobre estas raíces. \(\sigma\)Déjese entrar\(G(E/F)\) y supongamos que\(\sigma( \zeta ) = \omega^i \zeta\) y\(\tau( \zeta ) = \omega^j \zeta\text{.}\) Si\(F\) contiene las raíces de la unidad, entonces\(\tau\)

\[ \sigma \tau( \zeta ) = \sigma( \omega^j \zeta) = \omega^j \sigma( \zeta ) = \omega^{i+j} \zeta = \omega^i \tau( \zeta ) = \tau( \omega^i \zeta ) = \tau \sigma( \zeta )\text{.} \nonumber \]

Por lo tanto,\(\sigma \tau = \tau \sigma\) y\(G(E/F)\) es abeliano, y\(G(E/F)\) debe ser solucionable.

Ahora supongamos que eso\(F\) no contiene una primitiva raíz\(n\) th de unidad. \(\omega\)Sea un generador del grupo cíclico de las raíces\(n\) th de la unidad. Dejar\(\alpha\) ser un cero de\(x^n - a\text{.}\) Since\(\alpha\) y ambos\(\omega \alpha\) están en el campo de división de también\(x^n - a\text{,}\)\(\omega = (\omega \alpha)/ \alpha\) está en\(E\text{.}\) Let\(K = F( \omega)\text{.}\) Entonces\(F \subset K \subset E\text{.}\) Desde\(K\) es el campo de división de\(x^n - 1\text{,}\)\(K\) es una extensión normal de\(F\text{.}\) Por lo tanto, cualquier automorfismo\(\sigma\) en\(G(F( \omega)/ F)\) está determinado por\(\sigma( \omega)\text{.}\) Debe darse el caso de que\(\sigma( \omega ) = \omega^i\) para algún entero\(i\) ya que todos los ceros de\(x^n - 1\) son potencias de\(\omega\text{.}\) Si\(\tau( \omega ) = \omega^j\) está en\(G(F(\omega)/F)\text{,}\) entonces

\[ \sigma \tau( \omega ) = \sigma( \omega^j ) = [ \sigma( \omega )]^j = \omega^{ij} = [\tau( \omega ) ]^i = \tau( \omega^i ) = \tau \sigma( \omega )\text{.} \nonumber \]

Por lo tanto,\(G(F( \omega ) / F)\) es abeliano. Por el Teorema Fundamental de la Teoría Galois la serie

\[ \{ \identity \} \subset G(E/ F(\omega)) \subset G(E/F) \nonumber \]

es una serie normal. Por nuestro argumento anterior,\(G(E/F(\omega))\) es abeliano. Desde

\[ G(E/F) /G(E/F( \omega)) \cong G(F(\omega)/F) \nonumber \]

también es abeliano,\(G(E/F)\) es solucionable.

Lema\(23.29\).

Dejar\(F\) ser un campo de cero característico y dejar

\[ F = F_0 \subset F_1 \subset F_2 \subset \cdots \subset F_r = E \nonumber \]

una extensión radical de\(F\text{.}\) Entonces existe una extensión radical normal

\[ F = K_0 \subset K_1 \subset K_2 \subset \cdots \subset K_r = K \nonumber \]

tal\(K\) que contiene\(E\) y\(K_i\) es una extensión normal de\(K_{i-1}\text{.}\)

Prueba

Ya que\(E\) es una extensión radical de\(F\text{,}\) existe una cadena de subcampos

\[ F = F_0 \subset F_1 \subset F_2 \subset \cdots \subset F_r = E \nonumber \]

tal para\(i = 1, 2, \ldots, r\text{,}\) tenemos\(F_i = F_{i - 1}(\alpha_i)\) y\(\alpha_i^{n_i} \in F_{i-1}\) para algún entero positivo\(n_i\text{.}\) Vamos a construir una extensión radical normal de\(F\text{,}\)

\[ F = K_0 \subset K_1 \subset K_2 \subset \cdots \subset K_r = K \nonumber \]

tal que\(K \supseteq E\text{.}\) Definir\(K_1\) para ser el campo de división de\(x^{n_1} - \alpha_1^{n_1}\text{.}\) Las raíces de este polinomio son\(\alpha_1, \alpha_1 \omega, \alpha_1 \omega^2, \ldots, \alpha_1 \omega^{n_1 - 1}\text{,}\) donde\(\omega\) está una primitiva raíz\(n_1\) th de unidad. Si\(F\) contiene todas sus\(n_1\) raíces de unidad, entonces\(K_1 = F(\alpha_!)\text{.}\) Por otro lado, supongamos que\(F\) no contiene una primitiva raíz\(n_1\) th de unidad. Si\(\beta\) es una raíz de\(x^{n_1} - \alpha_1^{n_1}\text{,}\) entonces todas las raíces de\(x^{n_1} - \alpha_1^{n_1}\) deben estar\(\beta, \omega \beta, \ldots, \omega^{n_1-1}\text{,}\) donde\(\omega\) está una raíz primitiva\(n_1\) th de unidad. En este caso,\(K_1 = F(\omega \beta)\text{.}\) Así,\(K_1\) es una extensión radical normal de\(F\) contener\(F_1\text{.}\) Continuando de esta manera, obtenemos

\[ F = K_0 \subset K_1 \subset K_2 \subset \cdots \subset K_r = K \nonumber \]

tal que\(K_i\) es una extensión normal de\(K_{i-1}\) y\(K_i \supseteq F_i\) para\(i = 1, 2, \ldots, r\text{.}\)

Ahora vamos a probar el teorema principal sobre la solvabilidad por radicales.

Teorema\(23.30\).

Let\(f(x)\) be in\(F[x]\text{,}\) donde\(\chr F = 0\text{.}\)\(f(x)\) If es solucionable por radicales, entonces el grupo Galois de\(f(x)\) over\(F\) es solucionable.

Prueba

Dado que\(f(x)\) es solucionable por radicales existe una extensión\(E\) de\(F\)\(F = F_0 \subset F_1 \subset \cdots \subset F_n = E\text{.}\) por radicales Por Lema\(23.29\), podemos suponer que\(E\) es un campo de división\(f(x)\) y\(F_i\) es normal sobre\(F_{i - 1}\text{.}\) Por el Teorema Fundamental de la Teoría de Galois,\(G(E/F_i)\) es un subgrupo normal de\(G(E/F_{i - 1})\text{.}\) Por lo tanto, tenemos una serie subnormal de subgrupos de\(G(E/F)\text{:}\)

\[ \{ \identity \} \subset G(E/F_{n - 1}) \subset \cdots \subset G(E/F_1) \subset G(E/F)\text{.} \nonumber \]

Nuevamente por el Teorema Fundamental de la Teoría Galois, sabemos que

\[ G(E/F_{i - 1})/G(E/F_i) \cong G(F_i/F_{i - 1})\text{.} \nonumber \]

Por Lemma\(23.28\),\(G(F_i/F_{i - 1})\) es solucionable; por lo tanto, también\(G(E/F)\) es solucionable.

Lo contrario del teorema también\(23.30\) es cierto. Para una prueba, ver cualquiera de las referencias al final de este capítulo.

Insolvabilidad del Quíntico

Ahora estamos en condiciones de encontrar un polinomio de quinto grado que no es solucionable por radicales. Solo necesitamos encontrar un polinomio cuyo grupo Galois sea\(S_5\text{.}\) Empezamos por probar un lema.

Lema\(23.31\).

Si\(p\) es primo, entonces cualquier subgrupo de\(S_p\) ese contiene una transposición y un ciclo de duración\(p\) debe ser todo de\(S_p\text{.}\)

Prueba

\(G\)Sea un subgrupo de\(S_p\) que contenga una transposición\(\sigma\) y\(\tau\) un ciclo de longitud\(p\text{.}\) Podemos suponer que\(\sigma = (1 \, 2)\text{.}\) El orden de\(\tau\) es\(p\) y\(\tau^n\) debe ser un ciclo de longitud\(p\) para\(1 \leq n \lt p\text{.}\) Por lo tanto, podemos suponer que \(\mu = \tau^n = (1, 2, i_3, \ldots, i_p)\)para algunos\(n\text{,}\) donde\(1 \leq n \lt p\) (ver Ejercicio\(5.4.13\) en el Capítulo 5). Señalando que\((1 \, 2)(1, 2, i_3,\ldots, i_p) = (2, i_3, \ldots, i_p)\) y\((2,i_3, \ldots, i_p)^k(1 \, 2)(2,i_3, \ldots, i_p)^{-k} = (1 \, i_k)\text{,}\) podemos obtener todas las transposiciones de la forma\((1n)\) para\(1 \leq n \lt p\text{.}\) Sin embargo, estas transposiciones generan todas las transposiciones en\(S_p\text{,}\) ya que\((1 \, j)(1 \, i)(1 \, j) = (i \, j)\text{.}\) las transposiciones generan\(S_p\text{.}\)

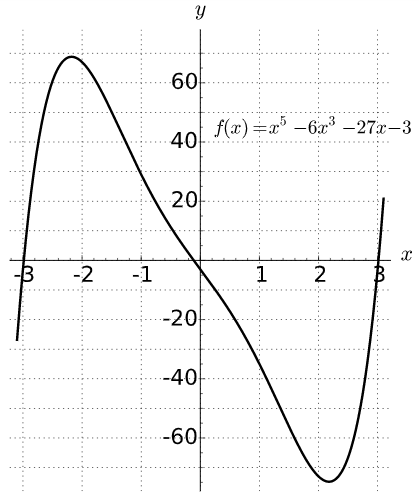
\(Figure \text { } 23.32.\)La gráfica de\(f(x) = x^5 - 6 x^3 - 27 x - 3\)

Ejemplo\(23.33\).

Demostraremos que no\(f(x) = x^5 - 6 x^3 - 27 x - 3 \in {\mathbb Q}[x]\) es solucionable. Afirmamos que el grupo Galois de\(f(x)\) más\({\mathbb Q}\) es\(S_5\text{.}\)

Solución

Por Criterio de Eisenstein,\(f(x)\) es irreducible y, por lo tanto, debe ser separable. El derivado de\(f(x)\) es\(f'(x) = 5 x^4 - 18 x^2 - 27\text{;}\) por lo tanto, establecer\(f'(x) = 0\) y resolver, encontramos que las únicas raíces reales de\(f'(x)\) son

\[ x = \pm \sqrt{ \frac{6 \sqrt{6} + 9 }{5} }\text{.} \nonumber \]

Por lo tanto,\(f(x)\) puede tener como máximo un máximo y un mínimo. Es fácil demostrar que\(f(x)\) los cambios de signo entre\(-3\) y\(-2\text{,}\) entre\(-2\) y\(0\text{,}\) y una vez más entre\(0\) y\(4\) (Figura\(23.32\)). Por lo tanto,\(f(x)\) tiene exactamente tres raíces reales distintas. Las dos raíces restantes de\(f(x)\) deben ser conjugados complejos. Let\(K\) be the splitting field of\(f(x)\text{.}\) Since\(f(x)\) tiene cinco raíces distintas en\(K\) y cada automorfismo de\(K\) fijación\({\mathbb Q}\) está determinado por la forma en que permuta las raíces de\(f(x)\text{,}\) sabemos que\(G(K/{\mathbb Q})\) es un subgrupo de\(S_5\text{.}\) Since\(f\) es irreducible, hay un elemento en\(\sigma \in G(K/{\mathbb Q})\) tal que\(\sigma(a) = b\) para dos raíces\(a\) y\(b\) de\(f(x)\text{.}\) El automorfismo de\({\mathbb C}\) eso toma las\(a + bi \mapsto a - bi\) hojas las raíces reales fijas e intercambia las raíces complejas; consecuentemente,\(G(K/{\mathbb Q} )\) contiene una transposición. Si\(\alpha\) es una de las raíces reales de\(f(x)\text{,}\) entonces\([\mathbb Q(\alpha) : \mathbb Q] = 5\) por Ejercicio\(21.5.28\). Ya que\(\mathbb Q(\alpha)\) es un subcampo del\(K\text{,}\) mismo debe ser el caso que\([K : \mathbb Q]\) sea divisible por 5. Ya\([K : \mathbb Q] = |G(K/{\mathbb Q})|\) y\(G(K/{\mathbb Q}) \subset S_5\text{,}\) sabemos que\(G(K/{\mathbb Q})\) contiene un ciclo de longitud\(5\text{.}\) Por Lema\(23.31\),\(S_5\) se genera por una transposición y un elemento de orden por\(5\text{;}\) lo tanto,\(G(K/{\mathbb Q} )\) debe ser todo de\(S_5\text{.}\) Por Teorema\(10.11\), no\(S_5\) es solucionable. En consecuencia,\(f(x)\) no pueden ser resueltos por radicales.

El teorema fundamental del álgebra

Parece apropiado que el último teorema que vamos a exponer y probar sea el Teorema Fundamental del Álgebra. Este teorema fue probado por primera vez por Gauss en su tesis doctoral. Antes de la prueba de Gauss, los matemáticos sospechaban que podrían existir polinomios sobre los números reales y complejos que no tienen soluciones. El Teorema Fundamental del Álgebra establece que cada polinomio sobre los números complejos factores en distintos factores lineales.

Teorema\(23.34\). Fundamental Theorem of Algebra.

El campo de los números complejos está cerrado algebraicamente; es decir, cada polinomio en\({\mathbb C}[x]\) tiene una raíz en\({\mathbb C}\text{.}\)

Prueba

Supongamos que\(E\) es una extensión de campo finita adecuada de los números complejos. Dado que cualquier extensión finita de un campo de cero característico es una extensión simple, existe una\(\alpha \in E\) tal que\(E = {\mathbb C}( \alpha )\) con\(\alpha\) la raíz de un polinomio irreducible\(f(x)\) en\({\mathbb C}[x]\text{.}\) El campo\(L\) de división de\(f(x)\) es una extensión separable normal finita de \({\mathbb C}\)que contiene\(E\text{.}\) Debemos demostrar que es imposible que\(L\) sea una extensión adecuada de\({\mathbb C}\text{.}\)

Supongamos que\(L\) es una extensión adecuada de\({\mathbb C}\text{.}\) Dado que\(L\) es el campo de división de\(f(x) = (x^2 + 1)\) over\({\mathbb R}\text{,}\)\(L\) es una extensión separable normal finita de\({\mathbb R}\text{.}\) Let\(K\) be el campo fijo de un subgrupo Sylow 2\(G\) de\(G(L/{\mathbb R})\text{.}\) Entonces\(L \supset K \supset {\mathbb R}\) y \(|G( L / K )| =[L:K]\text{.}\)Ya que\([L : {\mathbb R}] = [L:K][K:{\mathbb R}]\text{,}\) sabemos eso\([K:{\mathbb R}]\) debe ser extraño. En consecuencia,\(K = {\mathbb R}(\beta)\) con\(\beta\) tener un polinomio mínimo\(f(x)\) de grado impar. Por lo tanto,\(K = {\mathbb R}\text{.}\)

Ahora sabemos que\(G(L/{\mathbb R})\) debe ser un grupo de 2. De ello se deduce que\(G(L / {\mathbb C})\) es un\(2\) -grupo. Hemos asumido que\(|G(L / {\mathbb C})| \geq 2\text{.}\) por\(L \neq {\mathbb C}\text{;}\) lo tanto, Por el primer Teorema de Sylow y el Teorema Fundamental de la Teoría de Galois, existe un subgrupo\(G\)\(G(L/{\mathbb C})\) de de índice 2 y un campo\(E\) fijo elementwise por\(G\text{.}\) Entonces\([E:{\mathbb C}] = 2\) y existe un elemento\(\gamma \in E\) con polinomio mínimo\(x^2 + b x + c\) en\({\mathbb C}[x]\text{.}\) Este polinomio tiene raíces\(( - b \pm \sqrt{b^2 - 4c}\, ) / 2\) que están en\({\mathbb C}\text{,}\) ya que\(b^2 - 4 c\) está en\({\mathbb C}\text{.}\) Esto es imposible; de ahí,\(L = {\mathbb C}\text{.}\)

Aunque nuestra prueba era estrictamente algebraica, nos vimos obligados a confiar en los resultados del cálculo. Es necesario asumir el axioma de integridad a partir del análisis para mostrar que cada polinomio de grado impar tiene una raíz real y que cada número real positivo tiene una raíz cuadrada. Parece que no hay manera posible de evitar esta dificultad y formular un argumento puramente algebraico. Es algo sorprendente que haya varias pruebas elegantes del Teorema Fundamental del Álgebra que utilizan análisis complejos. También es interesante señalar que podemos obtener una prueba de un teorema tan importante a partir de dos campos muy diferentes de las matemáticas.