3.3: Los espacios nulos y de columna- Un ejemplo

Información Preliminar

Calculemos bases para los espacios nulos y columnas de la matriz de adyacencia asociada con la escalera de abajo.

Figura 1.

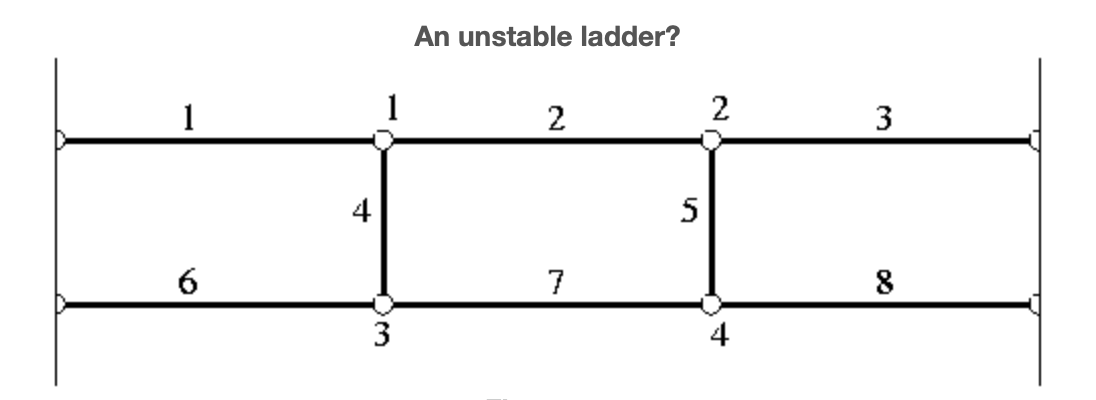
La escalera tiene 8 barras y 4 nodos, por lo que 8 grados de libertad. Denotando los desplazamientos horizontales y verticales del nodo j por\(x_{2j-1}\) y\(x_{2j}\) respectivamente, llegamos a la matriz A

\[A = \begin{pmatrix} {1}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {-1}&{0}&{1}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{-1}&{0}&{0}&{0}&{0}&{0}\\ {0}&{-1}&{0}&{0}&{0}&{1}&{0}&{0}\\ {1}&{0}&{0}&{0}&{1}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{-1}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{-1}&{0}\\ \end{pmatrix} \nonumber\]

Encontrar una base para el espacio de la columna

Para determinar una base para\(\mathcal{R}(⁢A)\) debemos encontrar la manera de descartar sus columnas dependientes. La reflexión de un momento revela que las columnas 2 y 6 son colineales, al igual que las columnas 4 y 8. Buscamos, por supuesto, un medio más sistemático de descubrir estas y quizás otras dependencias menos obvias. Tales dependencias se distinguen más fácilmente a partir de la forma de fila reducida

\[A_{red} = rref(A) = \begin{pmatrix} {1}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{1}&{0}&{0}&{0}&{-1}&{0}&{0}\\ {0}&{0}&{1}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{1}&{0}&{0}&{0}&{-1}\\ {0}&{0}&{0}&{0}&{1}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{1}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ \end{pmatrix} \nonumber\]

Recordemos que rref realiza las operaciones elementales de fila necesarias para eliminar todos los nonceros por debajo de la diagonal. Para los que no pueden soportar perderse ninguna de las acciones les recomiendo rrefmovie.

NOT_CONVERTED_YE: para

Cada fila distinta de cero de

\(A_{red}\)se llama fila de pivote. El primer distinto de cero en cada fila de\(A_{red}\) se llama pivote. Cada columna que contiene un pivote se llama columna pivote. Debido a la naturaleza de escalera de\(A_{red}\) encontramos que hay tantas columnas pivotantes como filas pivotantes. En nuestro ejemplo hay seis de cada una y, nuevamente por la naturaleza de la escalera, las columnas pivotes son las columnas linealmente independientes de\(A_{red}\) Uno ahora se pregunta cómo esto podría ayudarnos a distinguir las columnas independientes de A. Porque aunque las filas de\(A_{red}\) son combinaciones lineales de la filas de A, tal cosa no es cierta con respecto a las columnas. En nuestro ejemplo, las columnas\(\{1, 2, 3, 4, 5, 7\}\) son las columnas pivotantes. En general:

Proposición

Supongamos que A es m-por-n. Si las columnas\(\{c_{j} | j = 1, \cdots, r\}\) son las columnas pivotes de\(A_{red}\) entonces las columnas\(\{c_{j} | j = 1, \cdots, r\}\) de A constituyen una base para\(\mathcal{R}(⁢A)\).

Tenga en cuenta que las columnas pivotantes de ARedared son, por construcción, linealmente independientes. Supongamos, sin embargo, que las columnas\(\{c_{j} | j = 1, \cdots, r\}\) de A son linealmente dependientes. En este caso existe un distinto de cero\(x \in \mathbb{R}^{n}\) para el cual\(A \textbf{x} = \textbf{0}\) y

\[\forall k, k \notin \{c_{j} | j = 1, \cdots, r\} : (x_{k} = 0) \nonumber\]

Ahora implica\(A \textbf{x} = \textbf{0}\) necesariamente que\(A_{red} \textbf{x} = \textbf{0}\) contrariamente a que las columnas\(\{c_{j} | j = 1, \cdots, r\}\) son las columnas pivotes de\(A_{red}\)

Ahora mostramos que el lapso de columnas\(\{c_{j} | j = 1, \cdots, r\}\) de A efectivamente coincide con\(\mathbb{R}(⁢A)\) Esto es obvio si\(r = n\) es decir, si todas las columnas son linealmente independientes. Si\(r < n\) existe un\(q \notin \{c_{j} | j = 1, \cdots, r\}\) Mirando hacia atrás\(A_{red}\) observamos que su qésima columna es una combinación lineal de las columnas pivotes con índices que no excedan q. por lo tanto, existe una ecuación x satisfactoria\(A_{red} \textbf{x} = \textbf{0}\) y y\(x_{q} = 1\) Esta x entonces necesariamente satisface\(A \textbf{x} = \textbf{0}\). Esto establece que la qésima columna de A es una combinación lineal de columnas\(\{c_{j} | j = 1, \cdots, r\}\) de A

Encontrar una base para el espacio nulo

Expongamos ahora una base para\(\mathcal{N}(⁢A)\) Aprovechamos el hecho ya mencionado de que\(\mathcal{N}(A) = \mathcal{N}(A_{red})\). Respecto a esto último, particionamos los elementos de\(\textbf{x}\) en las llamadas variables pivotantes,

\[\{x_{c_{j}} | j = 1, \cdots, r\} \nonumber\]

y variables libres

\[\{x_{k} | k \notin \{x_{j} | j = 1, \cdots, r\}\} \nonumber\]

Evidentemente hay variables\(n-r\) libres. Para mayor comodidad, denotemos estos en el futuro por

\[\{x_{c_{j}} | j = r+1, \cdots, n\} \nonumber\]

Se resuelve\(A_{red} \textbf{x} = \textbf{0}\) expresando cada una de las variables pivotantes en términos de las variables no pivotantes o libres. En el ejemplo anterior,\(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\) y\(x_{7}\) son pivotantes mientras\(x_{6}\) y\(x_{8}\) son libres. Resolviendo para el pivote en cuanto a lo libre que encontramos

\[x_{7} = 0\]

\[x_{5} = 0\]

\[x_{4} = x_{8}\]

\[x_{3} = 0\]

\[x_{2} = x_{6}\]

\[x_{1} = 0\]

o, escrito como vector,

\[\textbf{x} = x_{6} \begin{pmatrix} {0}\\{1}\\{0}\\{0}\\{0}\\{1}\\{0}\\{0} \end{pmatrix}+x_{8} \begin{pmatrix} {0}\\{0}\\{0}\\{1}\\{0}\\{0}\\{0}\\{1} \end{pmatrix} \nonumber\]

donde\(x_{6}\) y\(x_{8}\) son libres. Como\(x_{6}\) y\(x_{8}\) rango sobre todos los números reales, lo\(\textbf{x}\) anterior traza un plano en\(\mathbb{R}^8\) Este plano es precisamente el espacio nulo de A y la ecuación describe un elemento genérico como la combinación lineal de dos vectores base. Compare esto con lo que devuelve MATLAB cuando se enfrenta a null (A, 'r'). Resumir estos cálculos llegamos a

Proposición

Supongamos que A es m-por-n con índices\(\{c_{j} | j = 1, \cdots, r\}\) de pivote e índices libres\(\{c_{j} | j = r+1, \cdots, n\}\) Una base para\(\mathcal{N}(A)\) puede construirse de\(n-r\) vectores\(\{z^{1}, z^{2}, \cdots, z^{n-r} \}\) donde\(z^{k}\) y solo\(z^k\) posee un distinto de cero en su\(c_{r+k}\) componente.

El significado físico de nuestros cálculos

Sin embargo, no terminemos con una nota abstracta. Preguntamos qué\(\mathcal{R}(⁢A)\) y\(\mathcal{N}(⁢A)\) cuéntanos sobre la escalera. En cuanto a\(\mathcal{R}(⁢A)\) la respuesta vendrá en el próximo capítulo. ¡Sin embargo, el cálculo del espacio nulo ha revelado dos movimientos independientes contra los cuales la escalera no funciona! ¿Ves que los dos vectores en Ecuación codifican movimientos verticales rígidos de barras 4 y 5 respectivamente? Como cada uno de estos yace en el espacio nulo de A Figure? Espero que no, para el movimiento vertical de la barra 4 hay que 'estirar' las barras 1, 2, 6 y 7. ¿Cómo se resuelve esta (aparente) contradicción?