11.8: Reflexión y simetría
- Page ID
- 109914
Reflexión y simetría en una línea
Supongamos que tenemos una línea\(S\) y un punto\(z_1\) no encendido\(S\). El reflejo de\(z_1\) in\(S\) es el punto de\(z_2\) manera que\(S\) es la bisectriza perpendicular al segmento de línea\(\overline{z_1 z_2}\). Dado que existe exactamente uno de esos puntos\(z_2\), el reflejo de un punto en una línea es único.
Si\(z_2\) es el reflejo de\(z_1\) in\(S\), decimos eso\(z_1\) y\(z_2\) son simétricos con respecto a la línea\(S\).
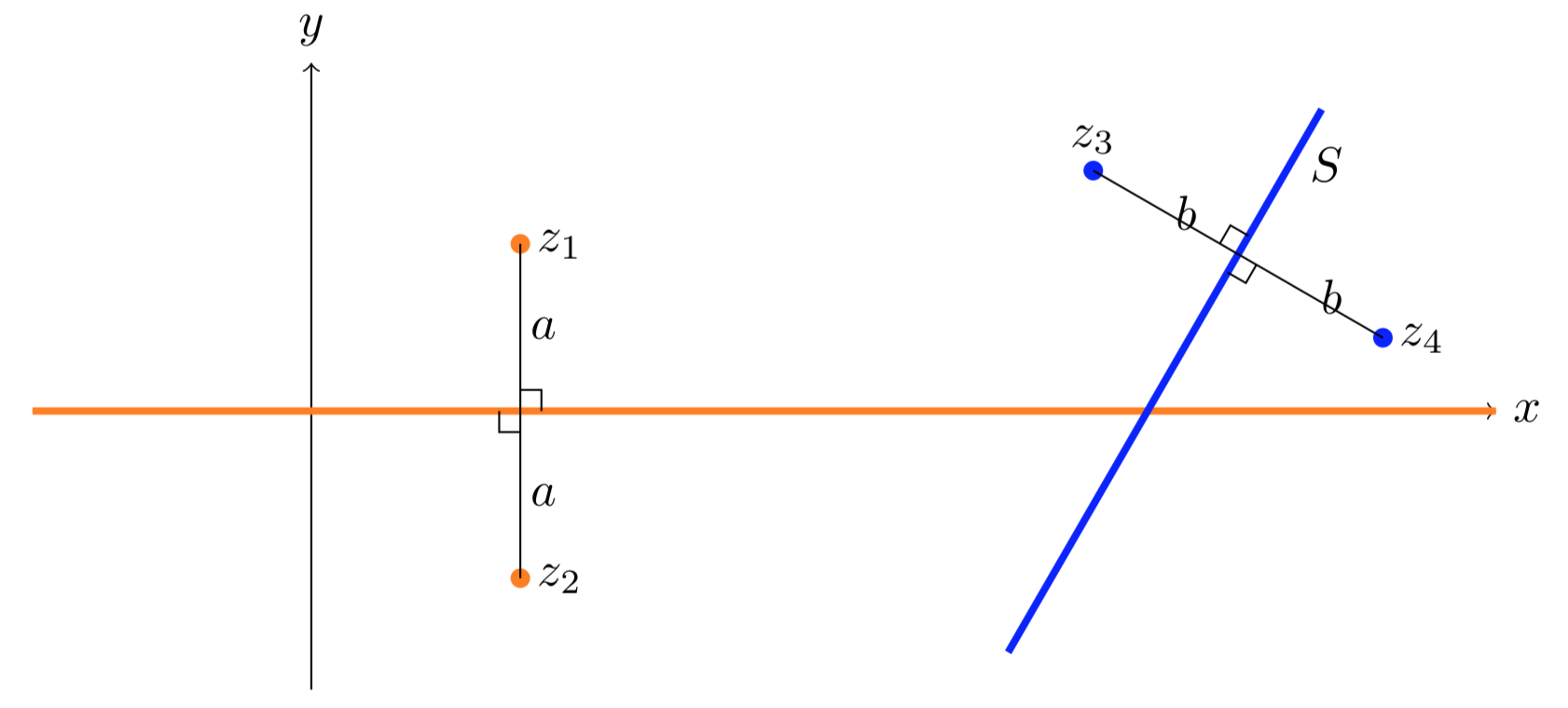
En la figura de abajo los puntos\(z_1\) y\(z_2\) son simétricos en el\(x\) eje -eje. Los puntos\(z_3\) y\(z_4\) son simétricos en la línea\(S\).
Para definir el reflejo de un punto en un círculo necesitamos trabajar un poco más duro. Mirando hacia atrás al ejemplo anterior podemos mostrar lo siguiente.
Si\(z_1\) y\(z_2\) son simétricos en la línea\(S\), entonces cualquier círculo a través\(z_1\) e\(z_2\) intersecta\(S\) ortogonalmente.
- Prueba
-
Llama al círculo\(C\). Ya que\(S\) es la bisectriz perpendicular de una cuerda de\(C\), el centro de\(C\) se encuentra sobre\(S\). Por lo tanto,\(S\) es una línea radial, es decir, se cruza\(C\) ortogonalmente.
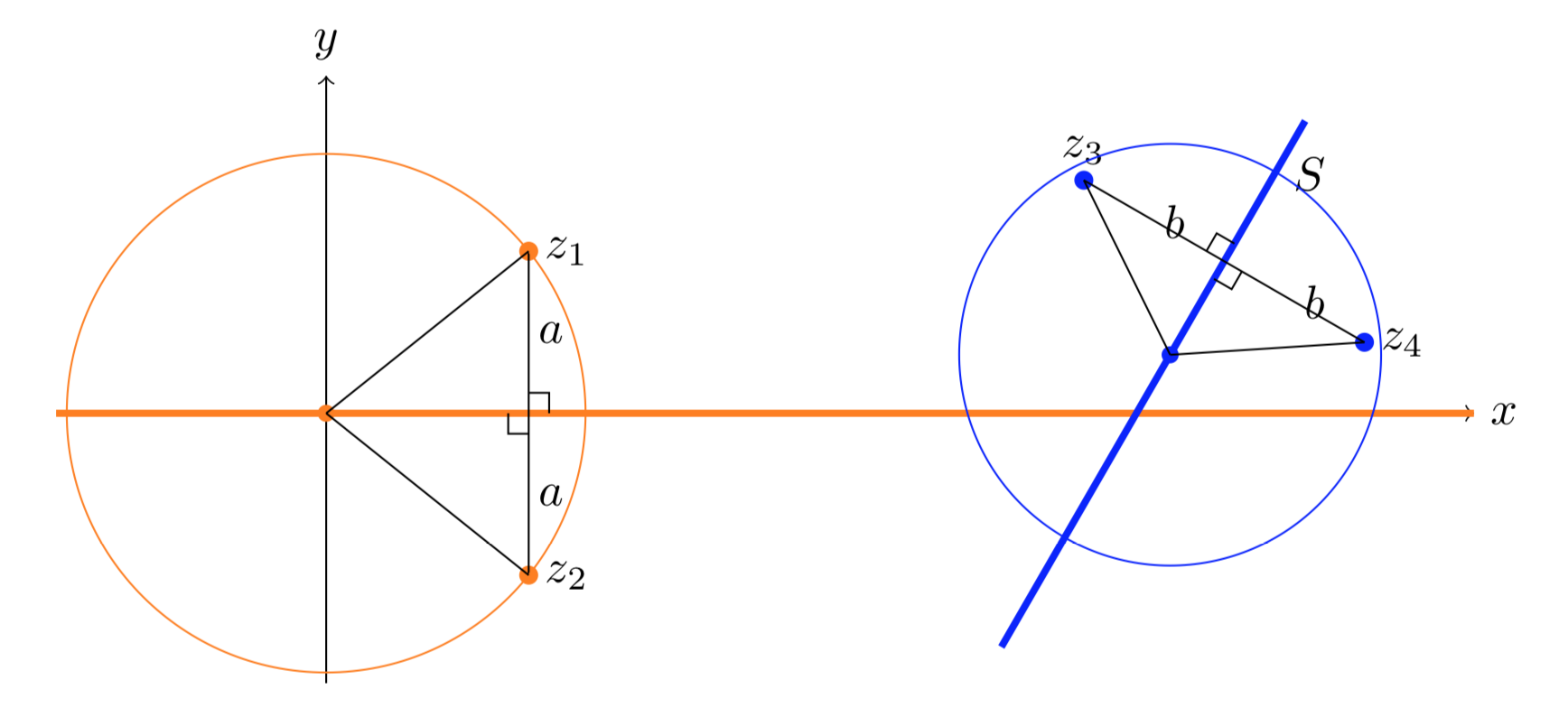
Círculos a través de puntos simétricos intersectan la línea en ángulo recto.
Reflexión y simetría en un círculo
Adaptaremos esto para nuestra definición de reflexión en círculo. Para que la lógica fluya correctamente necesitamos comenzar con la definición de pares simétricos de puntos.
Supongamos que\(S\) es una línea o círculo. Un par de puntos\(z_1, z_2\) se llama simétrico con respecto a\(S\) si cada línea o círculo a través de los dos puntos se cruza\(S\) ortogonalmente.
Primero declaramos un hecho casi trivial.
Las transformaciones lineales fraccionarias conservan la simetría. Es decir, si\(z_1, z_2\) son simétricos en una línea o círculo\(S\), entonces, para un FLT\(T\),\(T(z_1)\) y\(T(z_2)\) son simétricos en\(T(S)\).
- Prueba
-
La definición de simetría es en términos de líneas y círculos, y ángulos. Las transformaciones lineales fraccionarias mapean líneas y círculos a líneas y círculos y, al ser conformes, conservan los ángulos.
Supongamos que\(S\) es una línea o círculo y\(z_1\) un punto no encendido\(S\). Hay un punto único\(z_2\) tal que el par\(z_1, z_2\) es simétrico en\(S\).
- Prueba
-
Let\(T\) Ser una transformación lineal fraccionaria que se mapea\(S\) a una línea. Sabemos que\(w_1 = T(z_1)\) tiene un reflejo único\(w_2\) en esta línea. Ya que\(T^{-1}\) conserva la simetría,\(z_1\) y\(z_2 = T^{-1} (w_2)\) son simétricos en\(S\). Dado que\(w_2\) es el punto único simétrico a\(w_1\) lo mismo es cierto para\(z_2\) vis-a-vis\(z_1\). Todo esto se muestra en la siguiente figura.
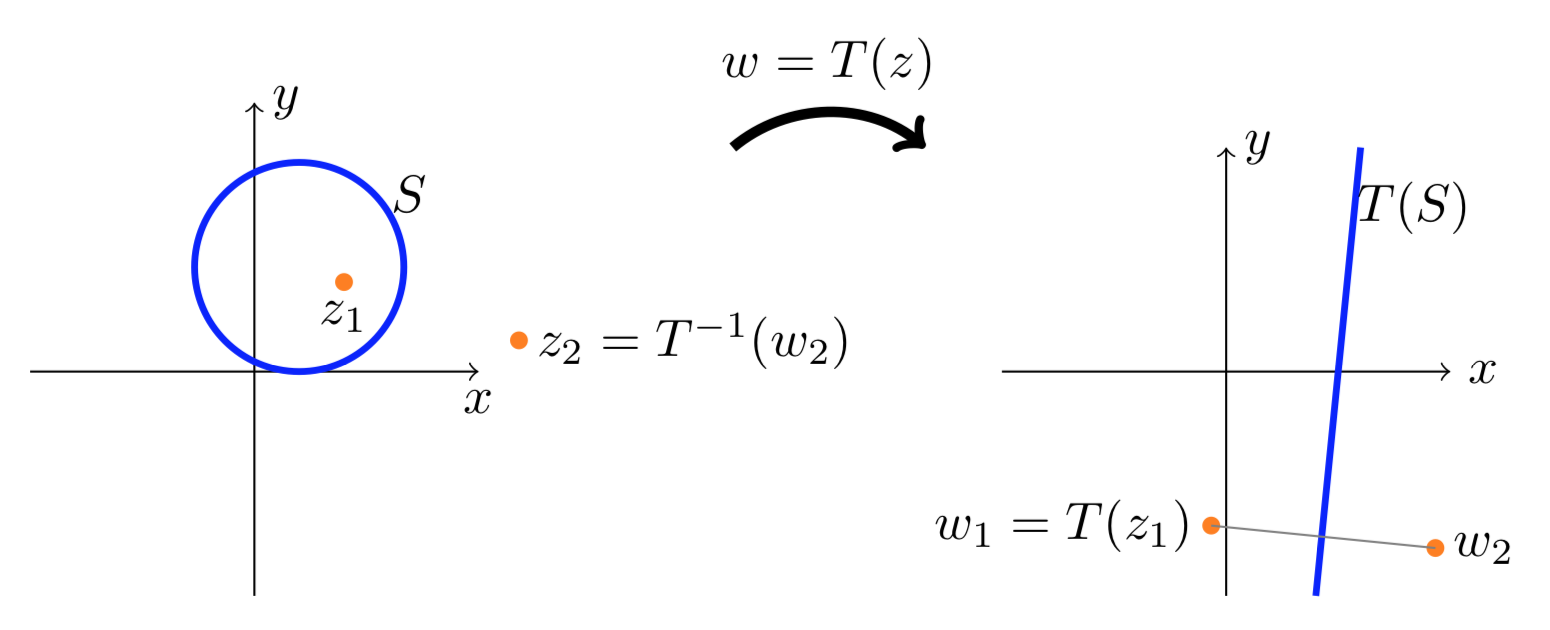
Ahora podemos definir la reflexión en un círculo.
El punto\(z_2\) en el Teorema 11.8.1 se llama el reflejo de\(z_1\) in\(S\).
Reflejo en el círculo unitario
Usando la característica de preservación de simetría de las transformaciones lineales fraccionarias, comenzamos con una línea y transformamos al círculo. \(R\)Dejen ser el eje real y\(C\) el círculo unitario. Conocemos el FLT
\[T(z) = \dfrac{z - i}{z + i}\]
mapas\(R\) a\(C\). También sabemos que los puntos\(z\) y\(\overline{z}\) son simétricos en\(R\). Por lo tanto
\[w_1 = T(z) = \dfrac{z - i}{z + i} \ \ \ \text{and} \ \ \ w_2 = T(\overline{z}) = \dfrac{\overline{z} - i}{\overline{z} + i}\]
son simétricos en\(D\). Al mirar las fórmulas, es claro que\(w_2 = 1/\overline{w_1}\). Esto es lo suficientemente importante como para destacarlo como teorema.
El reflejo de\(z = x + iy = re^{i \theta}\) en el círculo unitario es
\[\dfrac{1}{\overline{z}} = \dfrac{z}{|z|^2} = \dfrac{x + iy}{x^2 + y^2} = \dfrac{e^{i \theta}}{r}.\]
Los cálculos de\(1/\overline{z}\) son todos triviales.
- Es posible, pero más tedioso y menos perspicaz, llegar a este teorema por cálculo directo.
- Si\(z\) está en el círculo unitario entonces\(1/\overline{z} = z\). Es decir,\(z\) es su propio reflejo en el círculo unitario —como debería ser.
- El centro del círculo 0 es simétrico al punto en\(\infty\).
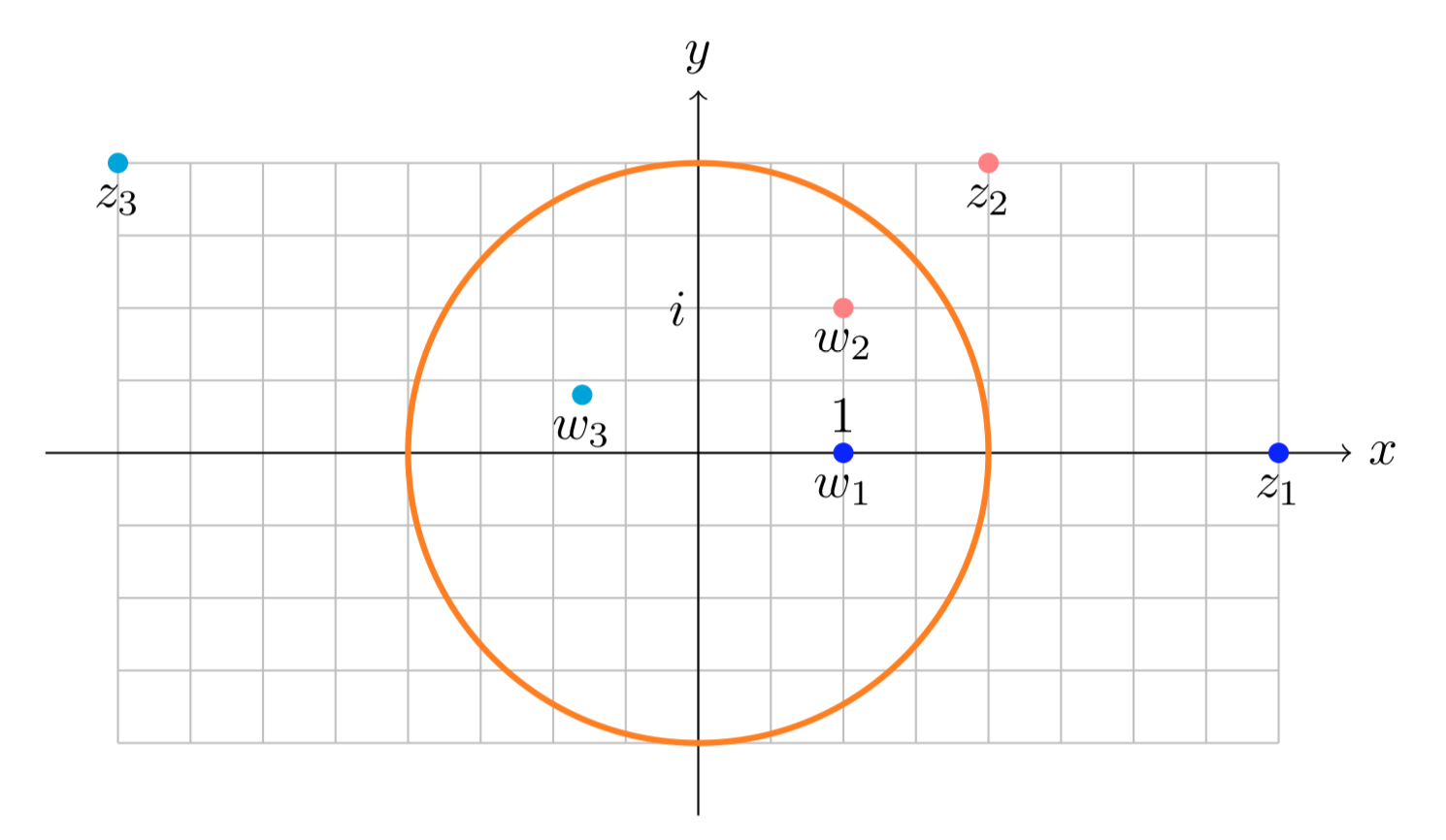
La siguiente figura muestra tres pares de puntos simétricos en el círculo unitario:
\(z_1 = 2; \ w_1 = \dfrac{1}{2}, \ z_2 = 1 + i; \ w_2 = \dfrac{1 + i}{2},\ z_3 = -2 + i; \ w_3 = \dfrac{-2 + i}{5}.\)
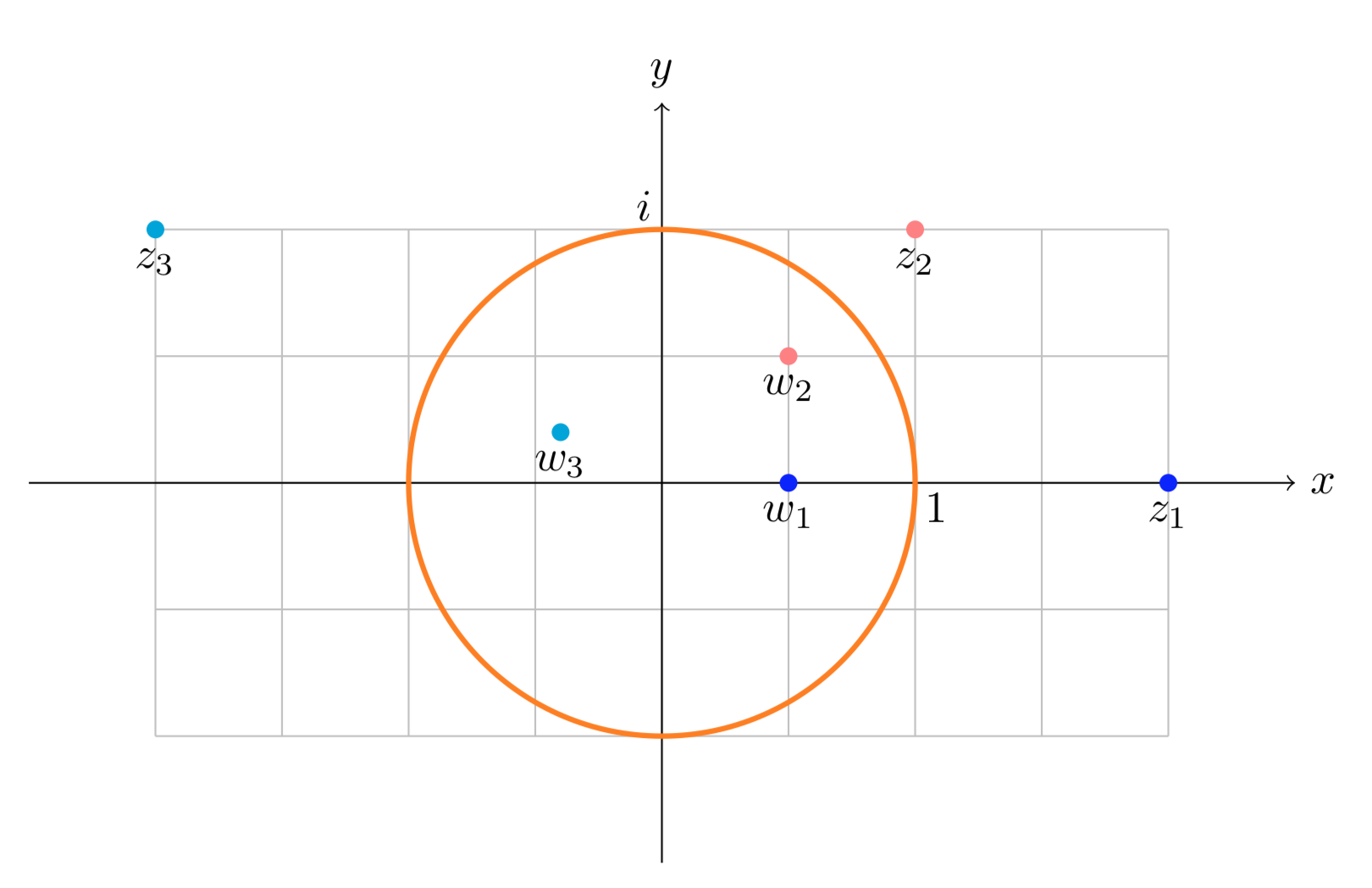
Pares de puntos\(z_j\):\(w_j\) simétricos en el círculo unitario.
Supongamos que\(S\)\(z_1\) es el círculo\(|z| = R\) y es una pinta no puesta\(S\). Encuentra el reflejo de\(z_1\) en S.
Solución
Nuestra estrategia es mapear\(S\) al círculo unitario, encontrar el reflejo y luego mapear el círculo unitario de nuevo a\(S\).
Comienza con el mapa\(T(z) = w = z/R\). Claramente\(S\) se\(T\) mapea al círculo de la unidad y
\[w_1 = T(z_1) = z_1/R.\]
El reflejo de\(w_1\) es
\[w_2 = 1/\overline{w_1} = R/\overline{z}_1.\]
Mapeo de vuelta desde el círculo de la unidad por\(T^{-1}\) tenemos
\[z_2 = T^{-1} (w_2) = Rw_2 = R^2/\overline{z}_1.\]
Por lo tanto el reflejo de\(z_1\) es\(R^2/\overline{z}_1.\)
Aquí hay tres pares de puntos simétricos en el círculo de radio 2. Tenga en cuenta, que esta es la misma cifra que la de arriba con todo duplicado.
\(z_1 = 4;\ w_1 = 1,\ z_2 = 2 + 2i;\ w_2 = 1 + i, \ z_3 = -4 + 2i;\ w_3 = \dfrac{-4 + 2i}{5}.\)
Pares de puntos\(z_j\);\(w_j\) simétricos en el círculo del radio 2.
Encuentra el reflejo de\(z_1\) en el círculo de radio\(R\) centrado en\(c\).
Solución
Vamos\(T(z) = (z - c)/R\). \(T\)mapea el círculo centrado en\(c\) al círculo unitario. El mapa inverso es
\[T^{-1} (w) = Rw + c.\]
Entonces, el reflejo de\(z_1\) se da mapeando\(z\) a\(T(z)\), reflejando esto en el círculo unitario, y mapeando de nuevo a la geometría original con\(T^{-1}\). Es decir, la reflexión\(z_2\) es
\[z_1 \to \dfrac{z_1 - c}{R} \to \dfrac{R}{\overline{z_1 - c}} \to z_2 = \dfrac{R^2}{\overline{z_1 - c}} + c.\]
Ahora podemos registrar el siguiente dato importante.
Para un círculo\(S\) con centro\(c\) el par\(c\),\(\infty\) es simétrico con respecto al círculo.
- Prueba
-
Esto es una consecuencia inmediata de la fórmula para la reflexión de un punto en un círculo. Por ejemplo, el reflejo de\(z\) en el círculo unitario es\(1/\overline{z}\). Entonces, el reflejo de 0 es infinito.
Mostrar que si un círculo y una línea no se cruzan entonces hay un par de puntos\(z_1, z_2\) que es simétrico con respecto tanto a la línea como al círculo.
Solución
Al desplazar, escalar y rotar podemos encontrar una transformación lineal fraccionaria\(T\) que mapea el círculo y la línea a la siguiente configuración: El círculo se mapea al círculo unitario y la línea a la línea vertical\(x = a > 1\).
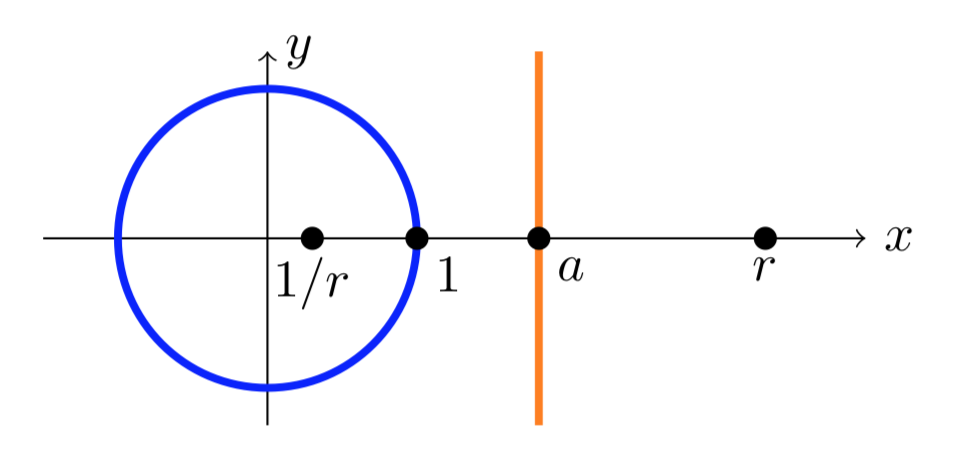
Para cualquier real\(r\),\(w_1 = r\) y\(w_2 = 1/r\) son simétricos en el círculo unitario. Podemos elegir un específico\(r\) para que\(r\) y\(1/r\) sean equidistantes de\(a\), es decir, también simétricos en la línea\(x = a\). Está claro geométricamente que esto se puede hacer. Algebraicamente resolvemos la ecuación
\[\dfrac{r + 1/r}{2} = a \ \ \Rightarrow \ \ r^2 - 2ar + 1 = 0 \ \ \Rightarrow \ \ r = a + \sqrt{a^2 - 1} \ \ \Rightarrow \ \ \dfrac{1}{r} = a - \sqrt{a^2 - 1}.\]
Así\(z_1 = T^{-1} (a + \sqrt{a^2 - 1})\) y\(z_2 = T^{-1} (a - \sqrt{a^2 - 1})\) son los puntos requeridos.
Demostrar que si dos círculos no se cruzan entonces hay un par de puntos\(z_1, z_2\) que es simétrico con respecto a ambos círculos.
Solución
Usando una transformación lineal fraccionaria que mapea uno de los círculos a una línea (y el otro a un círculo) podemos reducir el problema a eso en el ejemplo anterior.
Demuestre que dos círculos cualesquiera que no se crucen pueden mapearse conformalmente a círculos centrados.
Solución
Llama a los círculos\(S_1\) y\(S_2\). Usando el ejemplo anterior comienza con un par de puntos\(z_1, z_2\) que son simétricos en ambos círculos. A continuación, elija una transformación lineal fraccionaria\(T\) que se\(z_1\) mapee a 0 y\(z_2\) al infinito. Por ejemplo,
\[T(z) = \dfrac{z - z_1}{z - z_2}.\]
Ya que\(T\) conserva la simetría 0 y\(\infty\) son simétricas en el círculo\(T(S_1)\). Esto implica que 0 es el centro de\(T(S_1)\). Del mismo modo 0 es el centro de\(T(S_2)\). Así,\(T(S_1)\) y\(T(S_2)\) son concéntricos.