2.10: Optimización Aplicada
- Page ID
- 110594
Hemos utilizado derivados para ayudar a encontrar los máximos y mínimos de algunas funciones dadas por las ecuaciones, pero es muy poco probable que alguien simplemente te entregue una función y te pida que encuentres sus valores extremos. Más típicamente, alguien describirá un problema y te pedirá tu ayuda para maximizar o minimizar algo: ¿Cuál es el paquete de mayor volumen que llevará la oficina de correos?
; ¿Cuál es la manera más rápida de llegar de aquí a allá?
; o ¿Cuál es la forma menos costosa de realizar alguna tarea?
En esta sección, discutiremos cómo encontrar estos valores extremos usando cálculo.
Aplicaciones Max/Min
El gerente de una tienda de jardinería quiere construir un recinto rectangular de 600 pies cuadrados en el estacionamiento de la tienda con el fin de exhibir algunos equipos. Tres lados del recinto se construirán de esgrima de secoya, a un costo de $7 por pie corriendo. El cuarto lado se construirá de bloques de cemento, a un costo de 14 dólares por pie corriendo. Encuentre las dimensiones del gabinete de este tipo menos costoso.
El proceso de búsqueda de máximos o mínimos se llama optimización. La función que estamos optimizando se llama la función objetiva (o ecuación objetiva). La función objetiva puede reconocerse por su proximidad a las palabras est
(mayor, menor, más alta, más lejana, más,...). Mira el ejemplo de la tienda de jardinería; la función de costo es la función objetiva.
En muchos casos, hay dos (o más) variables en el problema. En el ejemplo de tienda de jardinería nuevamente, se desconocen tanto el largo como el ancho del recinto. Si hay una ecuación que relaciona las variables podemos resolver para una de ellas en términos de las otras, y escribir la función objetiva en función de una sola variable. Las ecuaciones que relacionan las variables de esta manera se denominan ecuaciones de restricción. Las ecuaciones de restricción son siempre ecuaciones, por lo que tendrán signos iguales. Para la tienda de jardinería, el área fija relaciona el largo y ancho del recinto. Esto nos dará nuestra ecuación de restricción.
- Traducir la declaración en inglés del problema línea por línea en una imagen (si eso aplica) y en matemáticas. ¡Este suele ser el paso más difícil!
- Identificar la función objetiva. Busque palabras que indiquen un valor mayor o menor.
- Si parece tener dos o más variables, busque la ecuación de restricción. Piense en el significado inglés de la palabra
restricción
y recuerde que la ecuación de restricción tendrá un signo igual. - Resolver la ecuación de restricción para una variable y sustituirla en la función objetiva. Ahora tienes una ecuación de una variable.
- Si parece tener dos o más variables, busque la ecuación de restricción. Piense en el significado inglés de la palabra
- Usa el cálculo para encontrar los valores óptimos. (Toma derivada, encuentra puntos críticos, prueba. ¡No te olvides de revisar los puntos finales!)
- Mira hacia atrás a la pregunta para asegurarte de que respondiste lo que se le hizo. Traduce tu respuesta de número de nuevo al inglés.
Aquí hay un enlace a los ejemplos utilizados en los videos de esta sección: Ejemplos de Optimización Aplicada.
El gerente de una tienda de jardinería quiere construir un recinto rectangular de 600 pies cuadrados en el estacionamiento de la tienda con el fin de exhibir algunos equipos. Tres lados del recinto se construirán de esgrima de secoya, a un costo de $7 por pie corriendo. El cuarto lado se construirá de bloques de cemento, a un costo de 14 dólares por pie corriendo. Encuentre las dimensiones del gabinete de este tipo menos costoso.
Primero, traduce línea por línea a matemáticas y una imagen:
| Texto | Traducción |
|
El gerente de una tienda de jardinería quiere construir un recinto rectangular de 600 pies cuadrados en el estacionamiento de la tienda con el fin de exhibir algunos equipos. Tres lados del recinto se construirán de esgrima de secoya, a un costo de $7 por pie corriendo. El cuarto lado se construirá de bloques de cemento, a un costo de 14 dólares por pie corriendo. Encuentre las dimensiones del gabinete de este tipo menos costoso. |
Dejar\(x\) y\(y\) ser las dimensiones del recinto,\(y\) siendo la longitud del lado hecho de bloques. Entonces:\[\text{Area} = A = xy = 600.\nonumber \] \(2x + y\)cuesta $7 por pie,\(y\) cuesta $14 por pie, entonces\[\text{Cost} = C = 7(2x + y) + 14y = 14x + 21y.\nonumber \] Encontrar\(x\) y\(y\) para que\(C\) se minimice. |
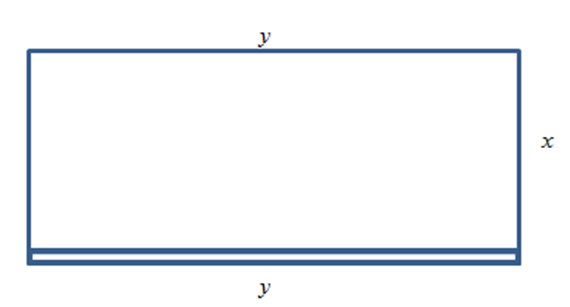
La función objetiva es la función costo, y queremos minimizarla. Tal como está, sin embargo, tiene dos variables, por lo que necesitamos usar la ecuación de restricción. La ecuación de restricción es el área fija\(A = xy = 600\). Resuelva\(A\)\(x\) para obtener\( x=\frac{600}{y} \), y luego sustituirlo en\(C\):\[C=14\left(\frac{600}{y}\right)+21y=\frac{8400}{y}+21y.\nonumber \]
Ahora tenemos una función de una sola variable, así podemos encontrar el mínimo usando cálculo.
\[C'=-\frac{8400}{y^2}+21\nonumber \]\(C'\)no está definido para\(y = 0\), y\(C' = 0\) cuando\(y = 20\) o\(y = -20\).
De estos tres números críticos, solo tiene\(y = 20\) sentido (está en el dominio de la función real) — recuerda que\(y\) es una longitud, por lo que no puede ser negativo, y\(y = 0\) significaría que no había ningún recinto en absoluto, por lo que no podría tener un área de 600 pies cuadrados.
Prueba\(y = 20\) (aquí elegimos la segunda prueba derivada):\[C''=\frac{16800}{y^3} \gt 0,\nonumber \] entonces esta es una mínima local.
Dado que este es el único punto crítico en el dominio, este debe ser el mínimo global. Volviendo a nuestra función de restricción, podemos encontrar que cuando\(y = 20\),\(x = 30\). Las dimensiones del gabinete que minimizan el costo son de 20 pies por 30 pies.
Al tratar de maximizar sus ingresos, las empresas también enfrentan la restricción de la demanda de los consumidores. Si bien a una empresa le encantaría ver muchos productos a un precio muy alto, normalmente la demanda disminuye a medida que aumenta el precio de los bienes. En casos simples, podemos construir esa curva de demanda para permitirnos maximizar los ingresos.
Una promotora de conciertos ha descubierto que si vende boletos por $50 cada una, puede vender 1200 boletos, pero por cada $5 que suba el precio, asisten 50 personas menos. ¿A qué precio debería vender los boletos para maximizar sus ingresos?
Estamos tratando de maximizar los ingresos, y lo sabemos\( R=pq \), dónde\(p\) está el precio por boleto, y\(q\) es la cantidad de boletos vendidos.
El problema proporciona información sobre la relación de demanda entre precio y cantidad — a medida que el precio aumenta, la demanda disminuye. Necesitamos encontrar una fórmula para esta relación. Para investigar, calculemos qué pasará con la asistencia si elevamos el precio:
| Precio,\( p \) | 50 | 55 | 60 | 65 |
| Cantidad,\( q \) | 1200 | 1150 | 1100 | 1050 |
Podrías reconocer esto como una relación lineal. Podemos encontrar la pendiente para la relación usando dos puntos:\[m=\frac{1150-1200}{55-50}=\frac{-50}{5}=-10.\nonumber \]
Podrán notar que el segundo paso en ese cálculo corresponde directamente a la declaración del problema: la asistencia baja a 50 personas por cada 5 dólares el precio aumenta.
Usando la forma punto-pendiente de la línea, podemos escribir la ecuación que relaciona precio y cantidad:\[q-1200=-10(p-50).\nonumber \]
Simplificar la forma de pendiente-intercepción da la ecuación de demanda\[ q=1700-10p. \nonumber \]
Sustituyendo esto en nuestra ecuación de ingresos, obtenemos una ecuación para ingresos que involucra solo una variable:\[R=pq=p(1700-10p)=1700p-10p^2.\nonumber \]
Ahora, podemos encontrar el máximo de esta función encontrando números críticos. \( R'=1700-20p \), así que\( R'=0 \) cuando\(p = 85\).
Usando la prueba de la segunda derivada,\( R''=-20 \lt 0 \) (para cualquier valor de\( p \)), por lo que el número crítico es un máximo local. Al ser el único número crítico, también podemos concluir que es el máximo global.
El promotor podrá maximizar los ingresos cobrando $85 por boleto. A este precio, venderá\( q=1700-10(85)=850 \) boletos, generando $72,250 en ingresos.
Ingresos Marginales = Costo Marginal
Es posible que hayas escuchado antes que las ganancias se maximizan cuando el costo marginal y los ingresos marginales son iguales.
¡Ahora puedes ver por qué la gente dice eso! (A pesar de que no es del todo cierto.)
Supongamos que queremos maximizar las ganancias.
Ahora sabemos qué hacer — encontrar la función de ganancia, encontrar sus puntos críticos, probarlos, etc.
Pero recuerda que Beneficio = Ingresos - Costo. Entonces Ganancia' = Ingresos' - Costo'. Es decir, la derivada de la función de ganancia es\(MR - MC\).
Ahora encontremos los puntos críticos —esos serán donde Profit' = 0 o es indefinido. Ganancia' = 0 cuando\(MR - MC = 0\), o donde\(MR = MC\).
La ganancia tiene puntos críticos cuando los ingresos marginales y los costos marginales son iguales.
En todos los casos veremos en esta clase, Profit se portará muy bien, y no tendremos que preocuparnos por buscar puntos críticos donde Profit' esté indefinido. Pero recuerda que no todos los puntos críticos son locales max! Los lugares donde\(MR = MC\) podrían representar local max, local min, o ninguno de los dos.
Una empresa vende bobinadoras de\(q\) cinta por año\(\$p\) por bobinadora de cinta. La función de demanda para las bobinadoras de cinta viene dada por:\(p=300-0.02q\). Las bobinadoras de cinta cuestan $30 cada una para fabricar, además hay costos fijos de $9000 por año. Encuentra la cantidad donde se maximiza el beneficio.
Queremos maximizar las ganancias, pero no se da una fórmula para el beneficio. Entonces vamos a hacer uno. Podemos encontrar una función para Ingresos =\(pq\) usando la función de demanda para\(p\). \[R(q)=(300-0.02q)q=300q-0.02q^2.\nonumber \]
También podemos encontrar una función para Costo, utilizando el costo variable de $30 por enrollador de cinta, más el costo fijo:\[C(q)=9000+30q.\nonumber \]
Al ponerlos juntos, obtenemos una función for Profit:\[P(q)=R(q)-C(q)=\left(300q-0.02q^2\right)-(9000+30q)=-0.02q^2+270q-9000\nonumber \]
Ahora tenemos dos opciones. Podemos encontrar los puntos críticos de Beneficio tomando la derivada de\(P(q)\) directamente, o podemos encontrarlos\(MR\)\(MC\) y establecerlos iguales. (Naturalmente, obtendremos la misma respuesta de cualquier manera).
Vamos a usar\(MR = MC\) este tiempo. \[ \begin{align*} MR & = 300-0.04q\\ MC & = 30\\ 300-0.04q & = 30\\ 270 & = 0.04q\\ q & = 6750 \end{align*} \nonumber \]
El único punto crítico está en\(q = 6750\). Ahora tenemos que estar seguros de que este es un máximo local y no un min local. En este caso, veremos la gráfica de\(P(q)\) — es una parábola de apertura hacia abajo, por lo que este debe ser un máximo local. Y como es el único punto crítico, también debe ser el máximo global.
Las ganancias se maximizan cuando venden 6750 bobinadoras de cinta.
Costo Promedio = Costo Marginal
El costo promedio se minimiza cuando costo promedio = costo marginal
es otro dicho que no es del todo cierto; en este caso, la afirmación correcta es:
El Costo Promedio tiene puntos críticos cuando el Costo Promedio y el Costo Marginal son iguales.
Veamos aquí un argumento geométrico. Recuerde que el costo promedio es la pendiente de la línea diagonal, la línea desde el origen hasta el punto en la curva de costo total. Si mueve su regla de plástico transparente, verá (y sentirá) que la pendiente de la línea diagonal es más pequeña cuando la línea diagonal solo toca la curva de costo, cuando la línea diagonal es en realidad una línea tangente, cuando el costo promedio es igual al costo marginal.
El costo en dólares para producir canastas de\(q\) regalo viene dado por\(C(q) = 160+2q+ .1q^2\). Encuentra la cantidad donde el costo promedio es mínimo.
Solución
\(A(q) = \frac{C(q)}{q} = \frac{160}{q} + 2 + .1q\). Podríamos encontrar los puntos críticos encontrando\(A'\), o estableciendo el costo promedio a costo marginal; esta vez haremos lo último.
\[MC(q) = 2+ .2q. \nonumber\]
Así que queremos resolver:
\[\begin{align*} \frac{160}{q} +2+.1q &= 2+.2q \\ \frac{160}{q} &= .1q \\ 1600 &= q^2 \\ q&=40 \end{align*}\]
El punto crítico de costo promedio es cuándo\(q = 40\).
Observe que aún tenemos que confirmar que el punto crítico es mínimo. Para ello, podemos usar la primera o segunda prueba derivada en\(A(q)\).
\[\begin{align*} A'(q) = \frac{-160}{q^2} +.1 \\ A''(q) = \frac{320}{q^3} >0 \end{align*}\]
La segunda derivada es positiva para todos los positivos\(q\), por lo que eso significa que se trata de un min local. El costo promedio se minimiza cuando producen 40 canastas de regalo; a esa cantidad, el costo promedio es de $10 por canasta.