2.3: El Derivado

Definición de la Derivada

Al trabajar con funciones lineales, podríamos encontrar la pendiente de una línea para determinar la velocidad a la que la función está cambiando. Para una función arbitraria, podemos determinar la tasa promedio de cambio de la función. Esta es la pendiente de la línea secante a través de esos dos puntos de la gráfica.

Tasa promedio de cambio

Tasa promedio de cambio =\( \dfrac{\Delta \text{output}}{\Delta \text{input}} = \dfrac{f(b) - f(a)}{b-a}\)

= la pendiente de la línea secante a través de los dos puntos\(\left(a, f(a)\right)\) y\(\left(b, f(b)\right)\)

Ejemplo\(\PageIndex{1}\)

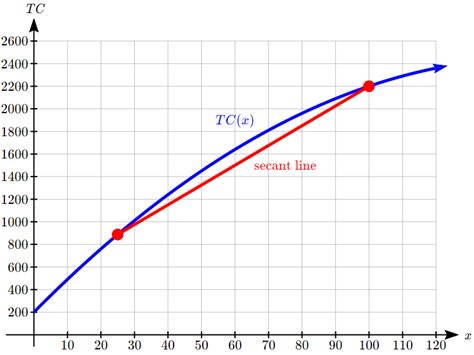
Supongamos que el costo total de producir\(x\) artículos viene dado por\(TC(x) = 200+30x-0.1x^2\). Determinar la tasa promedio de cambio de costo al aumentar la producción de 25 unidades a 100 unidades.

Solución

El costo al producir 25 unidades es\(TC(25) = 200+30(25)-0.1(25)^2 = \$887.50\)

El costo al producir 100 unidades es\(TC(100) = 200+30(100)-0.1(100)^2 = \$2200\)

El costo aumentó en $2200-$887.50 = $1312.50 mientras que la producción aumentó en 100 — 25 = 75 artículos. La tasa promedio de cambio es:
\[\frac{TC(100) - TC(25)}{100 - 25} = \frac{2200-887.50}{100-25} = \frac{1312.50}{75} = 17.50 \text{ dollars per unit}\nonumber \]

Esto nos dice que en promedio el costo aumenta en 17.50 dólares por cada unidad producida.

La tasa promedio de cambio es la pendiente de la línea secante entre (25, 887.50) y (100, 2200)

Pensando en el último ejemplo, supongamos que en cambio hicimos la pregunta “¿Qué tan rápido están aumentando los costos cuando la producción es de 25 unidades?” Observe que esta es una pregunta diferente. La pregunta del ejemplo planteaba la tasa de cambio a lo largo de un intervalo, ya que la producción aumentaba de un valor a otro. Esta pregunta vuelve a pedir una tasa de cambio, pero una tasa de cambio instantánea, en un momento determinado.

Todavía no tenemos una manera de calcular la tasa de cambio excepto en un intervalo. En el siguiente ejemplo exploraremos un par de formas de estimar la tasa instantánea de cambio.

Ejemplo\(\PageIndex{2}\)

Supongamos que el costo total de producir\(x\) artículos viene dado por\(TC(x) = 200+30x-0.1x^2\). Estimar la tasa instantánea de cambio cuando se producen 25 ítems.

Solución

Podemos ver en la gráfica anterior que la pendiente secante en el intervalo no\(25\leq x \leq 100\) es una estimación particularmente buena de la tasa de cambio instantánea ya que la función de costo parece más pronunciada en\(x = 25\) ese momento sobre la pendiente secante. Podríamos mejorar la estimación eligiendo un intervalo menor.

Enfoque 1: Uso de intervalos más pequeños

Usando el intervalo\(25\leq x \leq 30\), la tasa promedio de cambio sería:
\[\frac{TC(30) - TC(25)}{30 - 25} = \frac{1010-887.50}{30-25} = \frac{122.50}{5} = 24.50 \text{ dollars per unit}\nonumber \]

Usando un intervalo en el otro lado\(20\leq x \leq 25\),, la tasa promedio de cambio sería:
\[\frac{TC(25) - TC(20)}{25 - 20} = \frac{887.50-760}{25-20} = \frac{127.5}{5} = 25.50 \text{ dollars per unit}\nonumber \]

Visualmente, podemos ver que ambas líneas secantes parecen aproximarse bastante bien a la función.

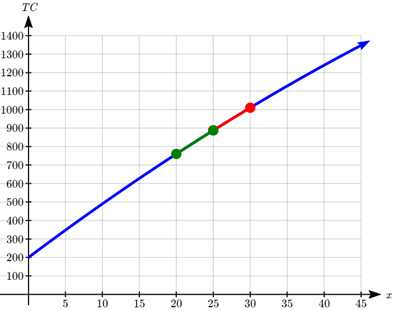
Esperaríamos que la tasa instantánea de cambio estuviera en algún lugar entre estos dos valores. Al promediarlos, obtenemos una estimación de $25 por unidad para la tasa de cambio instantánea.

Enfoque 2: Estimar a partir de la gráfica.

Este enfoque se usa más comúnmente cuando solo tenemos la gráfica de una función, y no tenemos una fórmula para evaluar, pero lo ilustraremos aquí usando la misma función.

La tasa instantánea de cambio es la pendiente de la línea tangente, que es la línea que apenas toca la gráfica en el punto de interés, y tiene la misma tasa de cambio (pendiente) que la función hace en el punto. Dada una gráfica, podemos bosquejar en una línea tangente sosteniendo una regla hasta la gráfica, y dibujando en una línea que toque la gráfica cuando\(x = 25\) y tenga la misma pendiente.

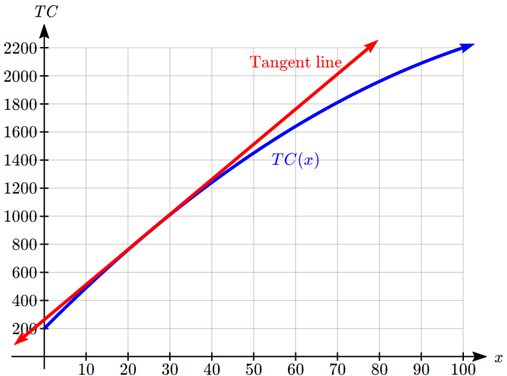
Para estimar la tasa instantánea de cambio, ahora podemos calcular la pendiente de esta línea dibujada. Al mirar la gráfica, la línea tangente parece pasar aproximadamente por (30, 1000) y (70, 2000) lo que daría una pendiente de\(\frac{2000-1000}{70-30}=\frac{1000}{40}=25\) dólares por unidad.

A continuación exploraremos las mismas ideas usando una función definida en una tabla, y en otro contexto.

Ejemplo\(\PageIndex{3}\)

Supongamos que dejamos caer un tomate desde lo alto de un edificio de 100 pies y cronometramos su caída.

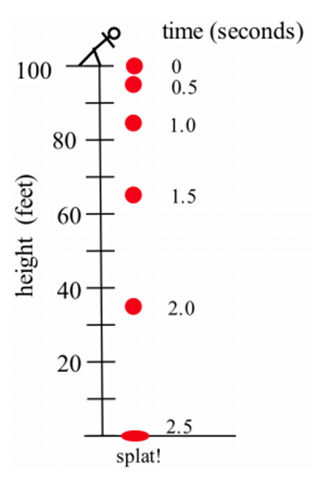
Tiempo (seg)	Altura (ft)
0.0	100
0.5	96
1.0	84
1.5	64
2.0	36
2.5	0

1. ¿Cuánto tiempo tardó el jitomate en caer 100 pies?
2. ¿Qué tan lejos cayó el jitomate durante el primer segundo?
3. ¿Qué tan lejos cayó el jitomate durante el último segundo?
4. ¿Hasta dónde cayó el jitomate entre\(t =0.5\) y\(t = 1\)?
5. ¿Cuál fue la velocidad promedio del tomate durante su caída?
6. ¿Cuál fue la velocidad promedio entre\( t=1\) y\(t=2\) segundos?
7. ¿Qué tan rápido cayó el jitomate 1 segundo después de que se le cayó?

Solución

Algunas de estas preguntas son bastante fáciles de responder, mientras que otras son más complejas.

1. De la mesa, tardaron 2.5 segundos para que el jitomate cayera 100 pies
2. Durante el primer segundo, el jitomate cayó 100 — 84 = 16 pies
3. Durante el último segundo, el jitomate cayó 64 — 0 = 64 pies
4. Entre\(t =0.5\) y\(t = 1\) el jitomate cayó 96 — 84 = 12 pies
5. La velocidad es similar a la velocidad, y es una tasa de cambio. Podemos calcular la velocidad promedio de la misma manera que hicimos la tasa promedio de cambio antes.
   \[\text{Average velocity}=\frac{\text{distance fallen}}{\text{total time}}=\frac{\Delta\text{position}}{\Delta\text{time}}=\frac{-100 \text{ ft}}{2.5 \text{ s}}=-40 \text{ ft/s}\nonumber \]
6. Entre\( t=1\) y\(t=2\) segundos,\[\text{Average velocity}=\frac{\Delta\text{position}}{\Delta\text{time}}=\frac{36\text{ ft}- 84\text{ ft}}{2\text{ s} - 1\text{ s}}=\frac{-48 \text{ ft}}{1 \text{ s}}=-48 \text{ ft/s}\nonumber \]
7. Esta pregunta es significativamente diferente de las dos preguntas anteriores sobre la velocidad promedio. Aquí queremos la velocidad instantánea, la velocidad en un instante en el tiempo. Desafortunadamente el tomate no está equipado con un velocímetro por lo que tendremos que dar una respuesta aproximada. Al igual que en nuestro Enfoque 1 del ejemplo anterior, lo estimaremos usando pendientes secantes.

Una aproximación cruda de la velocidad instantánea después de 1 segundo es simplemente la velocidad promedio durante toda la caída, -40 pies/s, pero el tomate cayó lentamente al principio y rápidamente cerca del final por lo que la estimación de “-40 pies/s” puede ser o no una buena respuesta.

Podemos obtener una mejor aproximación de la velocidad instantánea a\(t=1\) calculando las velocidades promedio en un corto intervalo tim e cercano\(t = 1\). La velocidad promedio entre\(t = 0.5\) y\(t = 1\) es\(\dfrac{-12\text{ feet}}{0.5\text{ s}} = -24\text{ ft/s}\), y la velocidad promedio entre\(t = 1\) y\(t = 1.5\) es\(\dfrac{-20\text{ feet}}{0.5\text{ s}} = -40\text{ ft/s}\) para que podamos estar razonablemente seguros de que la velocidad instantánea está entre -24 pies/s y -40 ft/s. El promedio, —32 ft/s, sería una buena estimación para r el velocidad instantánea.

En general, cuanto más corto sea el intervalo de tiempo sobre el cual calculamos la velocidad promedio, mejor será la velocidad promedio aproximada a la velocidad instantánea.

La velocidad promedio a lo largo de un intervalo de tiempo es\( \dfrac{\Delta\text{position}}{\Delta\text{time}} \), que es la pendiente de la línea secante a través de dos puntos en la gráfica de altura versus tiempo. La velocidad instantánea en un momento y altura particulares es la pendiente de la línea tangente a la gráfica en el punto dado por ese tiempo y altura.

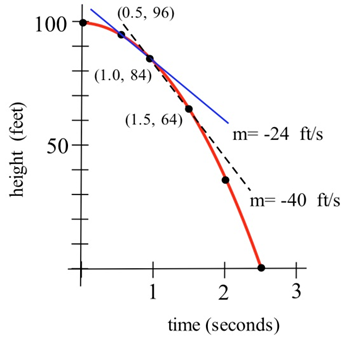
Velocidad promedio vs instantánea

Velocidad promedio =\( \dfrac{\Delta\text{position}}{\Delta\text{time}} \) = pendiente de la línea secante a través de 2 puntos.

Velocidad instantánea = pendiente de la línea tangente a la gráfica.

Ejemplo\(\PageIndex{4}\)

Supongamos que configuramos una máquina para contar el número de bacterias que crecen en una placa de Petri. Al principio hay pocas bacterias por lo que la población crece lentamente. Entonces hay más bacterias para dividir por lo que la población crece más rápidamente. Posteriormente, hay más bacterias y menos espacio y nutrientes disponibles para la población en expansión, por lo que la población vuelve a crecer lentamente. Finalmente, las bacterias han consumido la mayor parte de los nutrientes y la población disminuye a medida que mueren las bacterias.

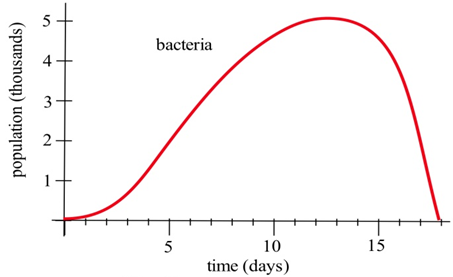
Utilice la gráfica de población para estimar la respuesta a las preguntas a continuación.

1. ¿Cuál es la población de bacterias en\(t = 3\) los días de tiempo?
2. ¿Cuál es el incremento poblacional de\(t = 3\) a\(t =10\) días?
3. ¿Cuál es la tasa de crecimiento poblacional de\(t = 3\) a\(t = 10\) días?
4. ¿Cuál es la tasa de crecimiento poblacional al tercer día, en\(t = 3\)?

Solución

1. De la gráfica, at\(t = 3\), la población es de aproximadamente 0.5 mil, o 500 bacterias.
2. At\(t = 10\), la población es de alrededor de 4.5 mil, por lo que el incremento es de alrededor de 4000 bacterias.
3. La tasa de crecimiento de\(t = 3\) a\(t = 10\) es la tasa promedio de cambio en la población durante ese tiempo:\[ \begin{align*} \text{average change in population } & = \frac{\text{change in population}}{\text{change in time}}\\ & = \frac{\Delta\text{population}}{\Delta\text{time}} \\ & = \frac{4000\text{ bacteria}}{7\text{ days}} \\ & \approx 570\text{ bacteria/day}. \end{align*} \nonumber \]

   Esta es la pendiente de la línea secante a través de los dos puntos (3, 500) y (10, 4500).

4. Esta pregunta pregunta por la tasa instantánea de cambio poblacional, la pendiente de la línea que es tangente a la curva poblacional en (3, 500). Si trazamos una línea aproximadamente tangente a la curva en (3, 500) y seleccionamos dos puntos cerca de los extremos del segmento de línea tangente, podemos estimar que la tasa instantánea de crecimiento poblacional es de aproximadamente 320 bacterias/día.

   

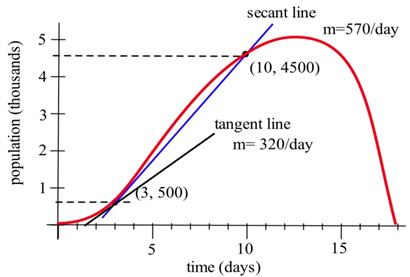
En los ejemplos anteriores, notamos que a medida que el intervalo se hacía cada vez más pequeño, la línea secante se acercaba a la línea tangente y su pendiente se acercaba a la pendiente de la línea tangente. Esa es una buena noticia —sabemos encontrar la pendiente de una línea secante.

Exploremos más a fondo esta idea de encontrar la pendiente tangente basada en la pendiente secante.

Ejemplo\(\PageIndex{5}\)

Encuentra la pendiente de la línea\(L\) en la gráfica de abajo que es tangente a\(f(x) = x^2\) en el punto (2,4).

Podríamos estimar la pendiente de\(L\) a partir de la gráfica, pero no lo haremos. En cambio, usaremos la idea de que las líneas secantes a intervalos diminutos se aproximan a la línea tangente.

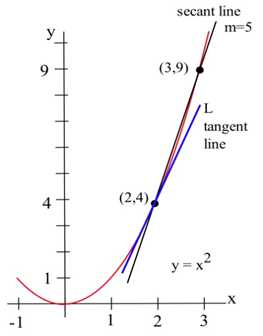
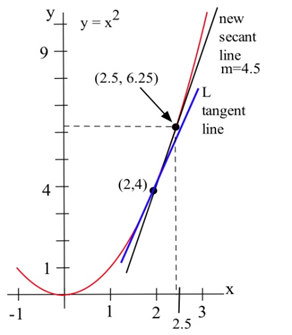
Podemos ver que la línea a través de (2,4) y (3,9) en la gráfica de\(f\) es una aproximación de la pendiente de la línea tangente, y podemos calcular esa pendiente exactamente:\(m = \frac{\Delta y}{\Delta x} = \frac{9-4}{3-2} = 5\). Pero\(m = 5\) es sólo una estimación de la pendiente de la línea tangente y no una estimación muy buena. Es demasiado grande. Podemos obtener una mejor estimación escogiendo un segundo punto en la gráfica del\(f\) cual está más cerca de (2,4). El punto (2,4) es fijo y debe ser uno de los puntos que usemos.

De la segunda figura, podemos ver que la pendiente de la línea a través de los puntos (2,4) y (2.5,6.25) es una mejor aproximación de la pendiente de la línea tangente en (2,4):\(m = \frac{\Delta y}{\Delta x} = \frac{6.25 - 4}{2.5 - 2} = \frac{2.25}{0.5} = 4.5 \), una mejor estimación, pero aún una aproximación. Podemos continuar recogiendo puntos cada vez más cercanos a (2,4) en la gráfica de\(f\), y luego calculando las pendientes de las líneas a través de cada uno de estos puntos y el punto (2,4):

Puntos a la izquierda de (2,4)

\( x \)	\( y=x^2 \)	Pendiente de línea pasante\( (x,y) \) y (2,4).
1.5	2.25	3.5
1.9	3.61	3.9
1.99	3.9601	3.99

Señala a la derecha de (2,4)

\( x \)	\( y=x^2 \)	Pendiente de línea pasante\( (x,y) \) y (2,4).
3	9	5
2.5	6.25	4.5
2.01	4.0401	4.01

Lo único especial de\(x\) los valores —que elegimos es que son números que están cerca, y muy cercanos, a\(x = 2\). Alguien más podría haber elegido otros valores cercanos para\(x\). A medida que los puntos que elegimos se acercan cada vez más al punto (2,4) en la gráfica de\( y = x^2\), las pendientes de las líneas a través de los puntos y (2,4) son mejores aproximaciones de la pendiente de la línea tangente, y estas pendientes se van acercando cada vez más a 4.

Podemos eludir gran parte del cálculo al no elegir los puntos uno a la vez: veamos un punto general cercano (2,4). Definir\( x = 2 + h\) así\(h\) es el incremento de 2 a\(x\). Si\(h\) es pequeño, entonces\(x = 2 + h\) está cerca de 2 y el punto\((2+h, f(2+h) ) = \left(2+h, (2+h)^2\right) \) está cerca de (2,4). La pendiente\(m\) de la línea a través de los puntos (2,4) y\(\left(2+h, (2+h)^2\right)\) es una buena aproximación de la pendiente de la línea tangente en el punto (2,4):

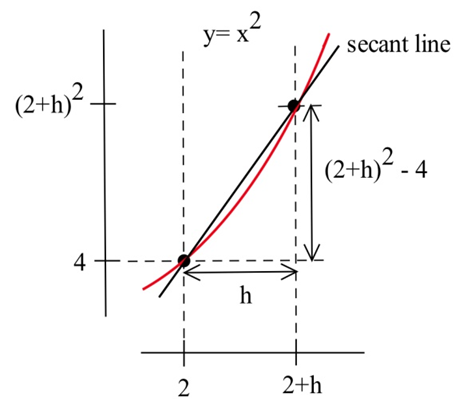
Podemos calcular la pendiente secante para cualquier valor de\(h\):

\[ m = \frac{\Delta y}{\Delta x} = \frac{(2+h)^2-4}{(2+h)-2} = \frac{\left(4+4h+h^2\right)-4}{h} = \frac{4h+h^2}{h} = \frac{h(4+h)}{h} = 4+h \nonumber\]

El valor\( m = 4 + h \) es la pendiente de la línea secante a través de los dos puntos (2,4) y\(\left( 2+h, (2+h)^2 \right)\). A medida que\(h\) se hace cada vez más pequeño, esta pendiente se acerca a la pendiente de la línea tangente a la gráfica de\(f\) at (2,4).

De manera más formal, podríamos escribir:\[\text{Slope of the tangent line} = \lim\limits_{h\to 0} \dfrac{\Delta y}{\Delta x} = \lim\limits_{h\to 0} (4+h). \nonumber \]

Podemos evaluar fácilmente este límite usando la sustitución directa, encontrando que a medida que el intervalo\(h\) se contrae hacia 0, la pendiente secante se acerca a la pendiente tangente, 4.

Usa el applet a continuación para explorar esto. Puede arrastrar el punto base en la gráfica para explorar el comportamiento en diferentes ubicaciones de la gráfica. Una vez establecido el punto base, use el control deslizante para ver cómo las líneas secantes se acercan a la línea tangente a medida que se\(h\) acerca a cero.

Encontrar pendientes tangentes y encontrar la tasa instantánea de cambio son el mismo problema. En cada problema queríamos saber cuán rápido algo estaba cambiando en un instante en el tiempo, y la respuesta resultó ser encontrar la pendiente de una línea tangente, que aproximamos con la pendiente de una línea secante. Esta idea es la clave para definir la pendiente de una curva.

La Derivada

Podemos ver la derivada de diferentes maneras. Aquí hay tres de ellos:

• La derivada de una función\(f\) en un punto\((x, f(x))\) es la velocidad instantánea de cambio.
• La derivada es la pendiente de la línea tangente a la gráfica de\(f\) en el punto\((x, f(x))\).
• La derivada es la pendiente de la curva\(f(x)\) en el punto\((x, f(x))\).

Una función se llama diferenciable en\((x, f(x))\) si su derivada existe en\((x, f(x))\).

Notación para la Derivada

La derivada de\(y = f(x)\) con respecto a\(x\) se escribe como\[f'(x)\nonumber \] (leer en voz alta como "\(f\)prima de\(x\) “), o\[y'\nonumber \] (leer en voz alta como “por qué prime”) o\[\frac{dy}{dx}\nonumber \] (leer en voz alta como “dee por qué dee ex”), o\[\frac{df}{dx}.\nonumber \]

La notación que se asemeja a una fracción se llama notación Leibniz. Muestra no sólo el nombre de la función (\(f\)o\(y\)), sino también el nombre de la variable (en este caso,\(x\)). Parece una fracción porque la derivada es una pendiente. De hecho, esto se\( \frac{\Delta y}{\Delta x} \) escribe simplemente en letras romanas en lugar de letras griegas.

Formas Verbales

Encontramos la derivada de una función, o tomamos la derivada de una función, o diferenciamos una función.

Usamos una adaptación de la\( \frac{df}{dx} \) notación para significar “encontrar la derivada de\(f(x)\):”\[\frac{d}{dx}\left[f(x)\right]=\frac{df}{dx}.\nonumber \] [El libro usa paréntesis en lugar de corchetes, ambos son formas aceptables de la notación.]

Definición Algebraica Formal

\[f'(x)=\lim\limits_{h\to 0} \dfrac{f(x+h)-f(x)}{h}\nonumber \]

Definición práctica

La derivada puede aproximarse observando una tasa promedio de cambio, o la pendiente de una línea secante, en un intervalo muy pequeño. Cuanto más pequeño sea el intervalo, más cerca está esto de la verdadera velocidad instantánea de cambio, pendiente de la línea tangente o pendiente de la curva.

Mirando hacia el futuro

Pronto tendremos métodos para computar valores exactos de derivados a partir de fórmulas. Si se le da la función como tabla o gráfica, aún necesitará aproximarse de esta manera.

Esta es la base para el resto de este capítulo. Es notable que una idea tan simple (la pendiente de una línea tangente) y una definición tan simple (para la derivada\( f'(x) \)) conduzcan a tantas ideas y aplicaciones importantes.

Ejemplo\(\PageIndex{6}\)

Encuentra la pendiente de la línea tangente a\( f(x)=\frac{1}{x} \) at\(x = 3\).

Solución

La pendiente de la línea tangente es el valor de la derivada\(f'(3)\). \( f(3)=\frac{1}{3}\)y\( f(3+h)=\frac{1}{3+h} \), por tanto, utilizando la definición de límite formal del derivado,\[ f'(3)=\lim\limits_{h\to 0}\frac{f(3+h)-f(3)}{h}=\lim\limits_{h\to 0}\frac{\frac{1}{3+h}-\frac{1}{3}}{h}. \nonumber \]

Podemos simplificar dando a las fracciones un denominador común:\[ \begin{align*} \lim\limits_{h\to 0}\frac{\frac{1}{3+h}-\frac{1}{3}}{h} & = \lim\limits_{h\to 0}\frac{\frac{1}{3+h}\cdot\frac{3}{3}-\frac{1}{3}\cdot\frac{3+h}{3+h}}{h} \\ & = \lim\limits_{h\to 0}\frac{\frac{3}{9+3h}-\frac{3+h}{9+3h}}{h} \\ & = \lim\limits_{h\to 0}\frac{\frac{3-(3+h)}{9+3h}}{h} \\ & = \lim\limits_{h\to 0}\frac{\frac{3-3-h}{9+3h}}{h} \\ & = \lim\limits_{h\to 0}\frac{\frac{-h}{9+3h}}{h} \\ & = \lim\limits_{h\to 0}\frac{-h}{9+3h}\cdot\frac{1}{h} \\ & = \lim\limits_{h\to 0}\frac{-1}{9+3h} \\ \end{align*} \] y la evaluación mediante sustitución directa:\[\lim\limits_{h\to 0}\frac{-1}{9+3h}=\frac{-1}{9+3(0)}=-\frac{1}{9}.\nonumber \]

Así, la pendiente de la línea tangente a\( f(x)=\frac{1}{x} \) at\(x = 3\) es\( -\frac{1}{9} \).

La Derivada como una Función

Ahora sabemos cómo encontrar (o al menos aproximarse) la derivada de una función para cualquier\(x\) -valor; esto significa que también podemos pensar en la derivada como una función. Las entradas son las mismas\(x\); la salida es el valor de la derivada en ese\(x\) valor.

Ejemplo\(\PageIndex{7}\)

A continuación se muestra la gráfica de una función\( y=f(x) \). Podemos usar la información de la gráfica para rellenar una tabla que muestre valores de\( f'(x): \)

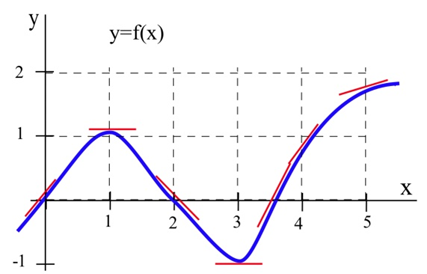
A varios valores de\(x\), dibuja tu mejor suposición en la línea tangente y mide su pendiente. Tal vez tengas que extender tus líneas para que puedas leer algunos puntos. En general, tu estimación de la pendiente será mejor si eliges puntos que sean fáciles de leer y alejados unos de otros. Aquí hay estimaciones para algunos valores de\(x\) (partes de las líneas tangentes utilizadas se muestran arriba en la gráfica):

\( x \)	\( y=f(x) \)	\( f'(x)= \)la pendiente estimada de la línea tangente a la curva en el punto\( (x,y) \).
0	0	1
1	1	0
2	0	-1
3	-1	0
3.5	0	2

Podemos estimar los valores de\(f'(x)\) en algunos valores no enteros de\(x\), también:\(f'(0.5) \approx 0.5\) y\(f'(1.3) \approx -0.3\).

Incluso podemos pensar en intervalos enteros. Por ejemplo, si\(0 \lt x \lt 1\), entonces\(f(x)\) va en aumento, todas las pendientes son positivas, y así\(f'(x)\) es positiva.

Los valores de\(f'(x)\) definitivamente dependen de los valores de\(x\), y\(f'(x)\) es una función de\(x\). Podemos utilizar los resultados en la tabla para ayudar a bosquejar la gráfica de\(f'(x)\).

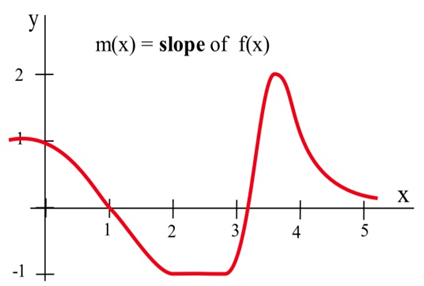
Para tener una mejor idea de esto, explore el applet a continuación. El gráfico superior es el gráfico de la función original\(g(x)\). La gráfica inferior muestra las pendientes de\(g(x)\), por lo que es una gráfica de la derivada,\(g'(x)\). Arrastre el punto a y observe cómo la pendiente de la línea tangente corresponde al valor de la derivada\(g'(x)\).

Ejemplo\(\PageIndex{8}\)

Se muestra la gráfica de la altura\(h(t)\) de un cohete en el momento\(t\).

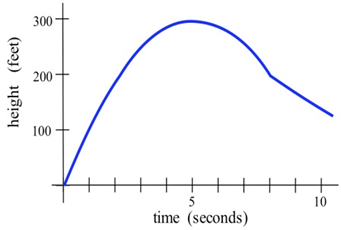
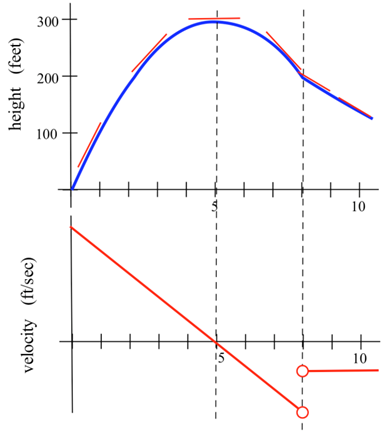
Dibuje el gráfico de la velocidad del cohete en el momento\(t\). (Velocidad es la derivada de la función height, por lo que es la pendiente de la tangente a la gráfica de posición o altura.)

Podemos estimar la pendiente de la función en varios puntos. El gráfico inferior a continuación muestra la velocidad del cohete. Esto es\(v(t) = h'(t)\).

En algunas aplicaciones, necesitamos saber dónde la gráfica de una función\(f(x)\) tiene líneas tangentes horizontales (pendientes = 0).

Ejemplo\(\PageIndex{9}\)

A continuación se muestra la gráfica de\(y = g(x)\). ¿A qué valores de\(x\) tiene la gráfica de\(g(x)\) líneas tangentes horizontales?

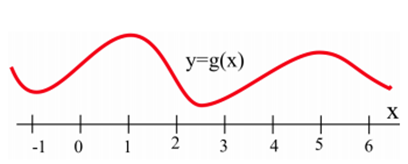
Las líneas tangentes a la gráfica de\(g(x)\) son horizontales (pendiente = 0) cuando\(x\approx -1, 1, 2.5, \text{ and } 5\).

También podemos encontrar funciones derivadas algebraicamente usando límites.

Ejemplo\(\PageIndex{10}\)

Encuentra\( \frac{d}{dx}\left( 2x^2-4x-1 \right) \).

Establecer la derivada usando un límite,\[ f'(x)=\lim\limits_{h\to 0}\frac{f(x+h)-f(x)}{h}.\nonumber \]

Empezaremos simplificando\( f(x+h) \) expandiendo:\[ \begin{align*} f(x+h) & = 2(x+h)^2-4(x+h)-1 \\ & = 2(x^2+2xh+h^2)-4(x+h)-1 \\ & = 2x^2+4xh+2h^2-4x-4h-1 \end{align*} \nonumber \]

Ahora encontrando el límite:\[ \begin{align*} f'(x) & = \lim\limits_{h\to 0}\frac{f(x+h)-f(x)}{h} \\ & = \lim\limits_{h\to 0} \frac{(2x^2+4xh+2h^2-4x-4h-1)-(2x^2-4x-1)}{h} \\ & = \lim\limits_{h\to 0} \frac{2x^2+4xh+2h^2-4x-4h-1-2x^2+4x+1}{h} \qquad \text{(Substitute in the formulas.)} \\ & = \lim\limits_{h\to 0} \frac{4xh+2h^2-4h}{h} \qquad \text{(Now simplify.)}\\ & = \lim\limits_{h\to 0} \frac{h(4x+2h-4)}{h} \qquad \text{(Factor out the \( h \), then cancel.)} \\ & = \lim\limits_{h\to 0} (4x+2h-4) \end{align*} \nonumber \] Podemos encontrar el límite de esta expresión por sustitución directa:\[ f'(x)=\lim\limits_{h\to 0} (4x+2h-4)=4x-4\nonumber \]

Observe que la derivada depende de\(x\), y que esta fórmula nos dirá la pendiente de la línea tangente\(f\) a cualquier valor\(x\). Por ejemplo, si quisiéramos conocer la pendiente tangente de\(f\) at\(x = 3\), simplemente evaluaríamos:\( f'(3)=4(3)-4=8 \).

Una fórmula para la función derivada es muy poderosa, pero como puedes ver, calcular la derivada usando la definición de límite lleva mucho tiempo. En la siguiente sección, identificaremos algunos patrones que nos permitirán comenzar a construir un conjunto de reglas para encontrar derivados sin necesidad de la definición de límite.

Interpretación de la Derivada

Hasta el momento hemos enfatizado la derivada como la pendiente de la recta tangente a una gráfica. Esa interpretación es muy visual y útil a la hora de examinar la gráfica de una función, y seguiremos utilizándola. Los derivados, sin embargo, se utilizan en una amplia variedad de campos y aplicaciones, y algunos de estos campos utilizan otras interpretaciones. A continuación se presentan algunas interpretaciones de la derivada que se utilizan comúnmente.

General

Tasa de Cambio:\(f '(x)\) es la tasa de cambio de la función a\(x\). Si las unidades para\(x\) son años y las unidades para\(f(x)\) son personas, entonces las unidades para\( \frac{df}{dx} \) son\(\frac{\text{people}}{\text{year}}\), una tasa de cambio en la población.

Gráfica

Pendiente:\(f '(x)\) es la pendiente de la línea tangente a la gráfica de\(f\) en el punto\(( x, f(x) )\).

Físico

Velocidad: Si\(f(x)\) es la posición de un objeto en el momento\(x\), entonces\(f '(x)\) es la velocidad del objeto a la vez\(x\). Si las unidades para\(x\) son horas y\(f(x)\) es distancia medida en millas, entonces las unidades para\(\mathbf{f '}(x) = \frac{df}{dx}\) son\( \frac{\text{miles}}{\text{hour}} \), millas por hora, que es una medida de velocidad.

Aceleración: Si\(f(x)\) es la velocidad de un objeto en el momento\(x\), entonces\(f '(x)\) es la aceleración del objeto a la vez\(x\). Si las unidades son para\(x\) son horas y\(f(x)\) tiene las unidades\( \frac{\text{miles}}{\text{hour}} \), entonces las unidades para la aceleración\(\mathbf{f '(x)} = \frac{df}{dx}\) son\( \frac{\text{miles/hour}}{\text{hour}} =\frac{\text{miles}}{\text{hour}^2} \), millas por hora por hora.

Negocios

Costo Marginal, Ingresos Marginales y Beneficio Marginal: Exploraremos estos términos con más profundidad más adelante en la sección. Básicamente, el costo marginal es aproximadamente el costo adicional de hacer un objeto más una vez que ya hemos hecho\(x\) objetos. Si las unidades para\(x\) son bicicletas y las unidades para\(f(x)\) son dólares, entonces las unidades para\(f '(x) = \frac{df}{dx}\) son\( \frac{\text{ dollars}}{\text{ bicycle}} \), el costo por bicicleta.

En contextos empresariales, la palabra "marginal" suele significar la derivada o tasa de cambio de alguna cantidad.

Una de las fortalezas del cálculo es que proporciona una unidad y economía de ideas entre diversas aplicaciones. El vocabulario y los problemas pueden ser diferentes, pero las ideas e incluso las notaciones del cálculo siguen siendo útiles.

Ejemplo\(\PageIndex{11}\)

Supongamos que la curva de demanda de widgets fue dada por\( D(p)=\frac{1}{p} \), donde\(D\) está la cantidad de widgets, en miles, a un precio de\(p\) dólares. Interpretar la derivada de\(D\) a\(p = \) $3.

Tenga en cuenta que calculamos\( D'(3) \) antes para ser\( D'(3)=-\frac{1}{9}\approx -0.111 \).

Ya que\(D\) tiene unidades miles de widgets y las unidades para\(p\) es dólares de precio, las unidades para\(D'\) serán\( \frac{\text{thousands of widgets}}{\text{dollar of price}} \). Es decir, muestra cómo va a cambiar la demanda a medida que aumente el precio.

Específicamente, nos\( D'(3)\approx -0.111 \) dice que cuando el precio es de $3, la demanda disminuirá en alrededor de 0.111 mil artículos por cada dólar el precio incremente.

(Nota: Las capturas de pantalla en el siguiente video son de una versión anterior del libro, por lo que algunos de los números de sección o títulos pueden no tener el mismo aspecto. No obstante, gran parte del contenido es el mismo, y los comentarios siguen aplicándose.)