2.9: Croquizado de curvas

Esta sección examina parte de la interacción entre la forma de la gráfica\(f\) y el comportamiento de\(f'\). Si tenemos una gráfica de\(f\), veremos qué podemos concluir sobre los valores de\(f'\). Si conocemos valores de\(f'\), veremos qué podemos concluir sobre la gráfica de\(f\). También utilizaremos la información de la\(f''\) que aprendamos en la última sección.

Información de Primera Derivada

Definiciones

La función\(f(x)\) está aumentando sobre\((a,b)\) si\(a \lt x_1 \lt x_2 \lt b\) implica\(f( x_1 ) \lt f( x_2 )\).

La función\(f(x)\) está disminuyendo en\((a,b)\) si\(a \lt x_1 \lt x_2 \lt b\) implica\(f( x_1 ) \gt f( x_2 )\).

Gráficamente,\(f\) es creciente (decreciente) si, a medida que nos movemos de izquierda a derecha a lo largo de la gráfica de\(f\), la altura de la gráfica aumenta (disminuye).

Estas mismas ideas tienen sentido si consideramos\(h(t)\) que es la altura (en pies) de un cohete a tiempo\(t\) segundos. Naturalmente decimos que el cohete está subiendo o que su altura va aumentando si la altura\(h(t)\) aumenta a lo largo de un periodo de tiempo, a medida que\(t\) aumenta.

Ejemplo\(\PageIndex{1}\)

Enumere los intervalos en los que la función mostrada es creciente o decreciente.

\(f\)está aumentando en los intervalos [0,0.5], [2,3] y [4,6].

\(f\)está disminuyendo en [0.5,2] y [6,8].

En el intervalo [3,4] la función no aumenta ni disminuye — es constante.

Información de la Primera Derivada sobre Forma

Para una función\(f\) que es diferenciable en un intervalo\((a,b)\);

• si\(f\) va aumentando en\((a,b)\), entonces\(f'(x) \geq 0\) para todos\(x\) adentro\((a,b)\).
• si\(f\) está disminuyendo en\((a,b)\), entonces\(f'(x) \leq 0\) para todos\(x\) en\((a,b)\).
• si\(f\) es constante encendido\((a,b)\), entonces\(f'(x) = 0\) para todos\(x\) adentro\((a,b)\).

Ejemplo\(\PageIndex{2}\)

La gráfica muestra la altura de un helicóptero durante un periodo de tiempo. Dibuje el gráfico de la velocidad ascendente del helicóptero,\( \frac{dh}{dt} \).

Observe que el\( h(t)\) tiene un máximo local cuando\(t = 2 \) y\(t = 5\), y así\(v(2) = 0\) y\(v(5) = 0\). De igual manera,\(h(t)\) tiene un mínimo local cuando\(t = 3\), así\(v(3) = 0\).

Cuando\(h\) va en aumento,\(v\) es positivo. Cuando\(h\) es decreciente,\(v\) es negativo.

Usando esta información, podemos bosquejar una gráfica de\(v(t) = \frac{dh}{dt}\).

El siguiente teorema es casi lo contrario del Teorema de la Primera Forma y explica la relación entre los valores de la derivada y la gráfica de una función desde una perspectiva diferente. Dice que si sabemos algo sobre los valores de\(f'\), entonces podemos sacar algunas conclusiones sobre la forma de la gráfica de\(f\).

Información de la Primera Derivada sobre la Forma (parte 2)

Para una función\(f\) que es diferenciable en un intervalo\(I\);

• si\(f'(x) \gt 0\) para todos\(x\) en el intervalo\(I\), entonces\(f\) está aumentando en\(I\).
• si\(f'(x) \lt 0\) para todos\(x\) en el intervalo\(I\), entonces\(f\) está disminuyendo en\(I\).
• si\(f'(x) = 0\) para todos\(x\) en el intervalo\(I\), entonces\(f\) es constante encendido\(I\).

Ejemplo\(\PageIndex{3}\)

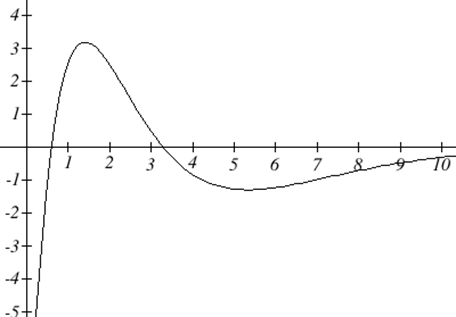
Use información sobre los valores de\(f'\) para ayudar a graficar\(f(x) = x^3 - 6x^2 + 9x + 1\).

Solución

\(f'(x) = 3x^2 - 12x + 9 = 3(x - 1)(x - 3)\)así que\(f'(x) = 0\) sólo cuando\(x = 1\) o\(x = 3\). \(f'\)es un polinomio por lo que siempre se define.

Los únicos números críticos para\(f\) son\(x = 1\) y\(x = 3\), y dividen la línea numérica real en tres intervalos:\((-\infty, 1)\),\((1,3)\), y\((3, \infty)\). En cada uno de estos intervalos, la función es siempre creciente o siempre decreciente.

Si\(x \lt 1\), entonces\(f '(x) =\) 3 (número negativo) (número negativo)\(\gt 0\) por lo que\(f\) está aumentando.

Si\(1 \lt x \lt 3\), entonces\(f'(x) =\) 3 (número positivo) (número negativo)\(\lt 0\) así\(f\) es decreciente.

Si\(x \gt 3\), entonces\(f'(x) =\) 3 (número positivo) (número positivo)\(\gt 0\) por lo que\(f\) va en aumento.

Aunque aún no conocemos el valor de\(f\) ninguna parte, sí sabemos mucho sobre la forma de la gráfica de\(f\): a medida que nos movemos de izquierda a derecha a lo largo del\(x\) eje -eje, la gráfica de\(f\) aumenta hasta\(x = 1\), luego la gráfica disminuye hasta\(x = 3\), y luego la gráfica aumenta otra vez. La gráfica de\(f\) hace “giros” cuando\(x = 1\) y\(x = 3\); tiene un máximo local en\(x = 1\), y un mínimo local en\(x = 3\).

Para trazar la gráfica de\(f\), todavía necesitamos evaluar\(f\) a unos pocos valores de\(x\), pero solo a muy pocos valores. \(f(1) = 5\), y (1,5) es un máximo local de\(f\). \(f(3) = 1\), y (3,1) es un mínimo local de\(f\). Aquí se muestra la\(f\) gráfica resultante de.

Información de Segunda Derivada

Hasta ahora, solo hemos usado información de la primera derivada, pero también podríamos usar información de la segunda derivada para proporcionar más información sobre la forma de la función.

Información de la Segunda Derivada sobre Forma

• Si\(f\) es cóncavo hacia arriba\((a,b)\), entonces\(f''(x) \geq 0\) para todos\(x\) adentro\((a,b)\).
• Si\(f\) es cóncavo hacia abajo\((a,b)\), entonces\(f''(x) \leq 0\) para todos\(x\) adentro\((a,b)\).

Lo contrario de ambos también es cierto:

• Si\(f''(x) \geq 0\) para todos\(x\) en\((a,b),\) entonces\(f\) es cóncavo hacia arriba en\((a,b)\).
• Si\(f''(x) \leq 0\) para todos\(x\) en\((a,b),\) entonces\(f\) es cóncavo hacia abajo en\((a,b)\).

Ejemplo\(\PageIndex{4}\)

Use información sobre los valores de\(f''\) para ayudar a determinar los intervalos en los que la función\(f(x) = x^3 - 6x^2 + 9x + 1\) es cóncava hacia arriba y cóncava hacia abajo.

Solución

Para la concavidad, necesitamos la segunda derivada:\( f'(x)=3x^2-12x+9 \), entonces\( f''(x)=6x-12 \).

Para encontrar posibles puntos de inflexión, establezca la segunda derivada igual a cero. \( 6x-12=0 \), entonces\(x = 2\). Esto divide la recta numérica real en dos intervalos:\( (-\infty,2) \) y\( (2,\infty) \).

Porque\(x \lt 2\), la segunda derivada es negativa (por ejemplo,\( f''(0)=6(0)-12=-12 \)), así\(f\) es cóncava hacia abajo. Porque\(x \gt 2\), la segunda derivada es positiva, por lo que\(f\) es cóncava hacia arriba.

Podríamos haber incorporado esta información de concavidad al esbozar la gráfica para el ejemplo anterior, y de hecho podemos ver la concavidad reflejada en la gráfica mostrada.

Ejemplo\(\PageIndex{5}\)

Use información sobre los valores de\(f'\) y\(f''\) para ayudar a graficar\( f(x)=x^{2/3} \).

Solución

\( f'(x)=\frac{2}{3}x^{-1/3} \). Esto no está definido en\(x = 0\).

\( f''(x)=-\frac{2}{9}x^{-4/3} \). Esto también está indefinido en\(x = 0\).

Esto crea dos intervalos:\(x \lt 0\), y\( x \gt 0\).

En el intervalo\(x \lt 0\), podríamos probar un valor como\(x = -1\):\[ f'(-1)=\frac{2}{3}(-1)^{-1/3}=-\frac{2}{3} \nonumber \] y\[ f''(-1)=-\frac{2}{9}(-1)^{-4/3}=-\frac{2}{9}. \nonumber \]

\( f'(x) \)es negativo y\( f''(x) \) es negativo, por lo que podemos concluir que la función es decreciente y cóncava hacia abajo en este intervalo.

En el intervalo\(x \gt 0\), podríamos probar un valor como\(x = 1\):\[ f'(1)=\frac{2}{3}(1)^{-1/3}=\frac{2}{3} \nonumber \] y\[ f''(1)=-\frac{2}{9}(1)^{-4/3}=-\frac{2}{9}. \nonumber \]

\( f'(x) \)es positiva y\( f''(x) \) negativa, por lo que podemos concluir que la función está aumentando y cóncava hacia abajo en este intervalo.

También podemos calcular eso\( f(0)=0 \), dándonos un punto base para la gráfica. Usando esta información, podemos concluir que la gráfica debe verse así:

Croquizar sin una ecuación

Por supuesto, las calculadoras gráficas y las computadoras son excelentes para graficar funciones. El cálculo proporciona una manera de iluminar lo que puede estar oculto o fuera de la vista cuando graficamos usando tecnología. Más importante aún, el cálculo nos da una manera de ver las derivadas de funciones para las que no se da ninguna ecuación. Ya vimos la idea de esto en la Sección 2.3 donde esbozamos la derivada de dos gráficas estimando pendientes en las curvas.

Podemos resumir toda la información derivada sobre la forma en una tabla.

Resumen de Información Derivada sobre la Gráfica

\( f(x) \)	Incrementando	Disminuyendo	Cóncavo Arriba	Abajo cóncavo
\( f'(x) \)	\( + \)	\( - \)	Incrementando	Disminuyendo
\( f''(x) \)			\( + \)	\( - \)

Cuando\(f'(x) = 0\), la gráfica de\(f\) puede tener un máximo local o mín.

Cuando\(f''(x) = 0\), la gráfica de\(f\) puede tener un punto de inflexión.

Ejemplo\(\PageIndex{6}\)

El saldo bancario de una compañía\(B\), en millones de dólares,\(t\) semanas después de lanzar un nuevo producto se muestra en la gráfica a continuación. Dibuje una gráfica del saldo marginal, la tasa a la que el saldo bancario estaba cambiando con el tiempo.

Solución

Observe que dado que la línea tangente será horizontal aproximadamente\(t = 0.6\) y\(t = 3.2\), la derivada será 0 en esos puntos.

Podemos entonces identificar intervalos en los que la función original está aumentando o disminuyendo. Esto nos dirá cuándo la función derivada es positiva o negativa.

Intervalo	\( B(t) \)	\( B'(t) \)
\(0 \lt t \lt 0.6\)	Disminuyendo	Negativo
\( 0.6 \lt t \lt 3.2 \)	Incrementando	Positivo
\( t \gt 3.2 \)	Disminuyendo	Negativo

Parecen haber puntos de inflexión a aproximadamente\(t =1.5\) y\(t = 5.5\). En estos puntos, la derivada estará cambiando de creciente a decreciente o viceversa, por lo que la derivada tendrá un máximo o mínimo local en esos puntos.

Observando los intervalos de concavidad:

Intervalo	\( B(t) \)	\( B'(t) \)
\( 0 \lt t \lt 1.5 \)	Cóncavo Arriba	Incrementando
\( 1.5 \lt t \lt 5.5 \)	Abajo cóncavo	Disminuyendo
\( t \gt 5.5 \)	Cóncavo Arriba	Incrementando

Si quisiéramos un boceto más preciso de la función derivada, también podríamos estimar la derivada en algunos puntos:

\( t \)	\( B'(t) \)
0	-10
1.5	3
6	-1

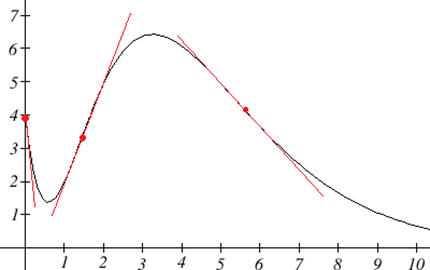
Ahora podemos bosquejar la derivada. Conocemos algunos valores para la función derivada, y en cada intervalo conocemos la forma que necesitamos. Podemos usar esto para crear una idea aproximada de cómo debería ser la gráfica.

Suavizar esto nos da una buena estimación para la gráfica de la derivada.