6.2: Grupos Actuando sobre Conjuntos

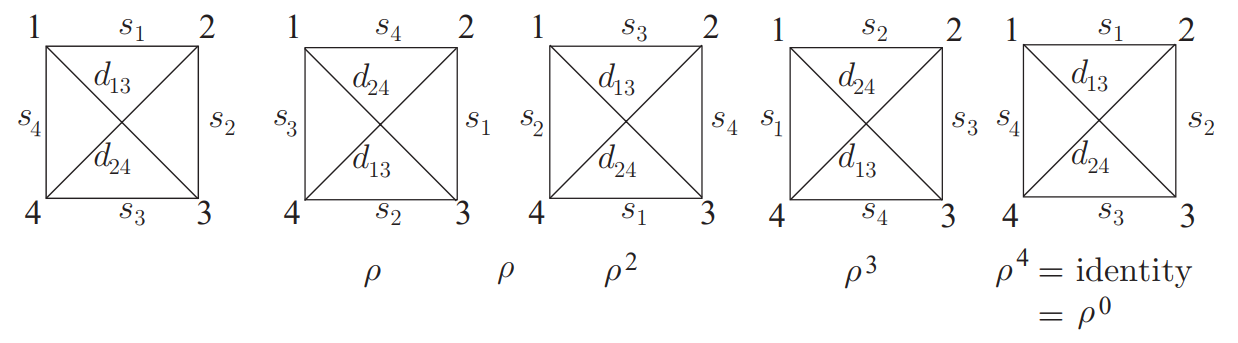
Definimos el grupo de rotación\(R_4\) y el grupo diedro\(D_4\) como grupos de permutaciones de los vértices de un cuadrado. Estas permutaciones representan movimientos rígidos del cuadrado en el plano y en el espacio tridimensional respectivamente. El cuadrado tiene rasgos geométricos de interés distintos a sus vértices; por ejemplo, sus diagonales, o sus aristas. Cualquier movimiento geométrico del cuadrado que lo devuelva a su ubicación original lleva cada diagonal a una diagonal posiblemente diferente, y lleva cada borde a un borde posiblemente diferente. En la Figura 6.2.1 se muestran los resultados en los lados y diagonales de las rotaciones de un cuadrado. El grupo de rotación permuta los lados del cuadrado y permuta las diagonales del cuadrado a medida que gira el cuadrado. Así decimos que el grupo de rotación “actúa” en los lados y diagonales del cuadrado.

Figura\(\PageIndex{1}\): Los resultados en los lados y diagonales de rotación del cuadrado. (Copyright; autor vía fuente)

Ejercicio 279

1. Anote la notación de dos líneas para la permutación\(\overline{ρ}\) que hace una rotación de\(90\) grados a los lados del cuadrado.
2. Anote la notación de dos líneas para la permutación\(\overline{ρ^2}\) que hace una rotación de\(180\) grados a los lados del cuadrado.
3. ¿Es\(\overline{ρ^2} = \overline{ρ} ◦ \overline{ρ}\)? ¿Por qué o por qué no?
4. Anote la notación de dos líneas para la permutación\(\hat{ρ}\) que hace una rotación de\(90\) grados a las diagonales\(d_{13}\), y\(d_{24}\) del cuadrado.
5. Anote la notación de dos líneas para la permutación\(\widehat{ρ^2}\) que hace una rotación de\(180\) grados a las diagonales del cuadrado.
6. ¿Es\(\widehat{ρ^2} = \hat{ρ} ◦ \hat{ρ}\)? ¿Por qué o por qué no? ¿Qué permutación familiar es\(\widehat{ρ^2}\) en este caso?

Hemos visto que el hecho de que hayamos definido un grupo de permutación como las permutaciones de algún conjunto específico no nos impide pensar en los elementos de ese grupo como permutar también los elementos de algún otro conjunto. Para hacer un seguimiento de qué permutaciones de qué conjunto estamos usando para definir nuestro grupo y qué otro conjunto también se permuta, introducimos un nuevo lenguaje y notación. Vamos a decir que el grupo\(D_4\) “actúa” sobre los bordes y diagonales de un cuadrado y el grupo\(R\) de permutaciones de los vértices de un cubo que surgen de movimientos rígidos del cubo “actúa” sobre los bordes, caras, diagonales, etc. del cubo.

\(\bullet\) Exercise \(280\)

En la Figura 6.1.3 mostramos un cubo con las posiciones de sus vértices y caras etiquetadas. Al igual que con los movimientos de la plaza, dejamos que\(\varphi(x)\) sea la etiqueta del lugar donde el vértice anteriormente en posición\(x\) está ahora.

1. En Problema 263 escribimos en notación de dos filas la permutación\(ρ\) de los vértices que corresponde a rotar los\(90\) grados del cubo alrededor de un eje vertical a través de las caras\(t\) (para arriba) y\(u\) (para debajo). (Giramos de manera diestra alrededor de este eje, lo que significa que el vértice\(6\) va hacia atrás y el vértice\(8\) viene al frente). Escribe en notación de dos filas la permutación\(\overline{ρ}\) de las caras que corresponda a este miembro\(ρ\) de\(R\).
2. En Problema 263 escribimos en notación de dos filas la permutación\(\varphi\) que gira los\(120\) grados del cubo alrededor de la diagonal de vértice\(1\) a vértice\(7\) y lleva vértice\(8\) a vértice\(6\). Escribe en notación de dos filas la permutación\(\overline{\varphi}\) de las caras que corresponda a este miembro de\(R\).
3. En Problema 263 calculamos la notación de dos filas para\(ρ ◦ \varphi\). Ahora computa la notación de dos filas para\(\overline{ρ} ◦ \overline{\varphi}\) (se\(\overline{ρ}\) definió en la Parte 280a), y escribe en notación\(\overline{ρ ◦ \varphi}\) de dos filas la permutación de las caras que corresponde a la acción de la permutación\(ρ ◦ \varphi\) en las caras del cubo (para esta pregunta ayuda pensar geométricamente sobre qué movimiento del cubo se lleva a cabo por\(ρ ◦ \varphi\)). ¿De qué se observa\(\overline{ρ ◦ \varphi}\) y\(\overline{ρ} ◦ \overline{\varphi}\)?

Decimos que un grupo de permutación\(G\) actúa sobre un conjunto\(S\) si, para cada miembro\(σ\) de\(G\) hay una permutación\(\overline{σ}\) de\(S\) tal que

\(\overline{σ ◦ \varphi} = \overline{σ} ◦ \overline{\varphi}\)

para cada miembro\(σ\) y\(\varphi\) de\(G\). En Problema 280c viste un ejemplo de esta condición. Si pensamos intuitivamente\(ρ\) y\(\varphi\) como movimientos en el espacio, entonces seguir la acción de\(\varphi\) por la acción de\(ρ\) sí nos da la acción de\(ρ ◦ \varphi\). También podemos razonar directamente con las permutaciones en el grupo\(R\) de movimientos rígidos (rotaciones) del cubo para mostrar que\(R\) actúa sobre las caras del cubo.

Ejercicio\(281\)

Demostrar que un grupo\(G\) de permutaciones de un conjunto\(S\) actúa sobre\(S\) con\(\overline{\varphi} = \varphi\) para todos\(\varphi\) en\(G\).

\(\bullet\) Exercise \(282\)

El grupo\(D_4\) es un grupo de permutaciones de\(\{1, 2, 3, 4\}\) como en el Problema 255. Vamos a mostrar en este problema cómo actúa este grupo sobre los subconjuntos de dos elementos de\(\{1, 2, 3, 4\}\). En Problema 287 veremos una interpretación geométrica natural de esta acción. En particular, para cada subconjunto\(\{i, j\}\) de dos elementos de\(\{1, 2, 3, 4\}\) y cada miembro\(σ\) de\(D_4\) definimos\(σ(\{i, j\}) = \{σ(i), σ(j)\}\). Mostrar que con esta definición de\(σ\), el grupo\(D_4\) actúa sobre los subconjuntos de dos elementos de\(\{1, 2, 3, 4\}\).

\(\bullet\) Exercise \(283\)

Supongamos que\(σ\) y\(\varphi\) son permutaciones en el grupo\(R\) de movimientos rígidos del cubo. Ya hemos argumentado que cada movimiento rígido envía cara a cara. Así\(σ\) y\(\varphi\) ambos envían los vértices de una cara a los vértices de otra cara. Dejar\(\{h, i, j, k\}\) ser el conjunto de etiquetas junto a los vértices en una cara\(F\).

1. ¿Cuáles son las etiquetas al lado de los vértices de la cara a las\(F'\) que\(F\) se envía\(\varphi\)? (La función\(\varphi\) puede aparecer en su respuesta.)
2. ¿Cuáles son los próximos a los vértices de la cara a la\(F''\) que\(F'\) se envía\(σ\)?
3. ¿Cuáles son las etiquetas al lado de los vértices de la cara a las\(F'''\) que\(F\) se envía\(σ ◦ \varphi\)?
4. ¿Cómo acaba de demostrar que el grupo\(R\) actúa en las caras?

6.2.1: Grupos que actúan sobre colorantes de juegos

Recordemos que cuando te pidieron en el Problema 45 que encontraras el número de formas de colocar dos cuentas rojas y dos cuentas azules en las esquinas de un cuadrado libre para moverte en el espacio tridimensional, no pudiste aplicar el principio del cociente para responder a la pregunta. En cambio había que ver que se podía dividir el conjunto de seis listas de dos Rs y dos Bs en dos conjuntos, uno de tamaño dos en el que alternaban las Rs y Bs y otra de talla cuatro en la que los dos rojos (y por lo tanto los dos azules) estarían uno al lado del otro en la plaza. Decir que el cuadrado es libre de moverse en el espacio equivale a decir que dos arreglos de cuentas en el cuadrado son equivalentes si un miembro del grupo diedro lleva un arreglo al otro. Así, un ingrediente importante en el análisis de tales problemas será cómo un grupo puede actuar sobre los colorantes de un conjunto de vértices. Podemos describir la coloración del cuadrado en la Figura 6.2.2 como la función\(f\) con

\(f(1) = R, f(2) = R, f(3) = B, \text{ and } f(4) = B\),

pero es más compacto y resulta ser más sugerente para representar la coloración en la Figura 6.2.2 como el conjunto de pares ordenados

\[ (1, R),(2, R),(3, B),(4, B). \label{6.2.1}\]

Figura\(\PageIndex{2}\): El cuadrado coloreado con coloración\(\{(1, R),(2, R),(3, B),(4, B)\}\). (Copyright; autor vía fuente)

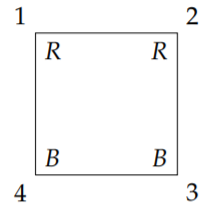
Esto nos da una lista explícita de qué colores se asignan a qué vértice. ¹ Entonces si giramos el cuadrado a través de\(90\) grados, vemos que el conjunto de pares ordenados se vuelve

\[\{(ρ(1), R),(ρ(2), R),(ρ(3), B),(ρ(4), B)\} \label{6.2.2} \]

que es lo mismo que

\(\{(2, R),(3, R),(4, B),(1, B)\}\).

o, en un orden más natural,

\[\{(1, B),(2, R),(3, R),(4, B)\}. \label{6.2.3} \]

El reordenamiento que hicimos\(\ref{6.2.3}\) sugiere otra simplificación de la notación. Siempre y cuando sepamos que los primeros elementos de nuestros pares son etiquetados por los miembros de\([n]\) para algún entero\(n\) y estamos listando nuestros pares en orden creciente por el primer componente, podemos denotar la coloración

\(\{(1, B),(2, R),(3, R),(4, B)\}\)

por\(BRRB\). En el caso donde hayamos numerado los elementos del conjunto\(S\) que estamos coloreando, llamaremos a esta lista de colores de los elementos de\(S\) en orden la notación estándar para la coloración. Llamaremos al pedido utilizado en\(\ref{6.2.3}\) el orden estándar de la coloración.

Así tenemos tres formas naturales de representar una coloración de un conjunto como una función, como un conjunto de pares ordenados, y como una lista. Diferentes representaciones son útiles para diferentes cosas. Por ejemplo, la representación por pares ordenados proporcionará una forma natural de definir la acción de un grupo sobre los colorantes de un conjunto. Dada una coloración como función\(f\), denotamos el conjunto de pares ordenados

\(\{(x, f(x))|x ∈ S\},\)

sugestivamente como\((S, f)\) para abreviar. Usamos\(f(1)f(2)· · · f(n)\) para representar una coloración particular\((S, f)\) en la notación estándar.

Ejercicio\(284\)

Supongamos ahora que en lugar de colorear los vértices de un cuadrado, coloreamos sus bordes. Usaremos la taquigrafía\(12\)\(23\),\(34\),, y\(41\) para representar los bordes del cubo entre vértice\(1\) y vértice\(2\), vértice\(2\) y vértice\(3\), y así sucesivamente. Entonces una coloración de los bordes con\(12\) rojo,\(23\) azul,\(34\) rojo y\(41\) azul se puede representar como

\[\{(12, R),(23, B),(34, R),(41, B)\}. \label{6.2.4} \]

Si\(ρ\) es la rotación a través de\(90\) grados, entonces tenemos una permutación\(\overline{ρ}\) que actúa sobre los bordes. Esta permutación actúa sobre los colorantes para darnos una permutación\(\overline{\overline{ρ}}\) del conjunto de colorantes.

1. ¿Qué es\(\overline{\overline{ρ}}\) de la coloración en\(\ref{6.2.4}\)?
2. ¿Qué es\(\overline{\overline{ρ^2}}\) de la coloración en\(\ref{6.2.4}\)?

Si G es un grupo que actúa el conjunto S, definimos la acción de G sobre los colorantes\((S, f)\) por

\[\overline{\overline{σ}}((S, f)) = \overline{\overline{σ}}(\{(x, f(x))|x ∈ S\}) = \{(\overline{σ}(x), f(x))|x ∈ S\}.. \label{6.1.5} \]

Tenemos las dos barras encima\(σ\), porque\(σ\) es una permutación de un conjunto que nos da una permutación\(\overline{σ}\) de un segundo conjunto, y luego\(\overline{σ}\) actúa para dar una permutación\(\overline{\overline{σ}}\) de un tercer conjunto, el conjunto de colorantes. Por ejemplo, supongamos que queremos anlayzar coloraciones de las caras de un cubo bajo la acción del grupo de rotación del cubo como lo hemos definido en los vértices. Cada permutación de vértices\(σ\) en el grupo da una permutación\(\overline{σ}\) de las caras del cubo. Entonces cada permutación\(\overline{σ}\) de los rostros nos da una permutación\(\overline{\overline{σ}}\) de los colores de los rostros.

En el caso especial que\(G\) es un grupo de permutaciones de\(S\) más que un grupo que actúa sobre\(S\), Ecuación\(\ref{6.1.5}\) se convierte en

\(σ((S, f)) = σ(\{(x, f(x))|x ∈ S\}) = \{(σ(x), f(x))|x ∈ S\}.\)

En el caso donde\(G\) está el grupo de rotación del cuadrado actuando sobre los vértices del cuadrado, el ejemplo de actuar sobre una coloración por la\(ρ\) que vimos en\(\ref{6.1.3}\) es un ejemplo de este tipo de acción. En la notación estándar, cuando actuamos sobre una coloración por\(σ\), el color en posición\(i\) se mueve a posición\(σ(i)\).

Ejercicio\(285\)

¿Por qué la acción que hemos definido sobre los colorantes en Ecuación\(\ref{6.1.5}\) lleva una coloración a una coloración?

Ejercicio\(286\)

Mostrar que si\(G\) es un grupo de permutaciones de un conjunto\(S\), y\(f\) es una función de coloración en\(S\), entonces la ecuación

\(\overline{\overline{σ}}(\{(x, f(x))|x ∈ S\}) = \{(\overline{σ}(x), f(x))|x ∈ S\}\)

define una acción de\(G\) sobre los colorantes\((S, f)\) de\(S\). (Pista).

6.2.2: Órbitas

\(\bullet\) Exercise \(287\)

En Problema 282

1. ¿Cuál es el conjunto de dos subconjuntos de elementos que obtienes al computar\(\overline{σ}(\{1, 2\})\) para all\(σ\) in\(D_4\)?
2. ¿Cuál es el multiconjunto de subconjuntos de dos elementos que obtienes al computar\(\overline{σ}(\{1, 2\})\) para todos\(σ\) en\(D_4\)?
3. ¿Cuál es el conjunto de subconjuntos de dos elementos que obtienes al computar\(\overline{σ}(\{1, 3\})\) para all\(σ\) in\(D_4\)?
4. ¿Cuál es el multiconjunto de subconjuntos de dos elementos que obtienes al computar\(\overline{σ}(\{1, 3\})\) para todos\(σ\) en\(D_4\)?
5. Describir los dos conjuntos en las partes a. y c. geométricamente en términos del cuadrado.

\(\bullet\) Exercise \(288\)

Este problema utiliza la notación para permutaciones en el grupo diedro del cuadrado introducido antes del Problema 259. ¿Cuál es el efecto de una rotación de\(180\) grados\(ρ^2\) en las diagonales de un cuadrado? ¿Cuál es el efecto del flip\(\varphi_{1|3}\) en las diagonales de un cuadrado? ¿Cuántos elementos de\(D_4\) enviar cada diagonal a sí mismo? ¿Cuántos elementos de\(D_4\) intercambio las diagonales de un cuadrado?

En Problema 287 viste que la acción del grupo diedro\(D_4\) sobre dos subconjuntos de elementos de\(\{1, 2, 3, 4\}\) parece dividirlos en dos bloques, uno con dos elementos y otro con\(4\). Llamamos a estos dos bloques las “órbitas” de\(D_4\) actuar sobre los dos subconjuntos de elementos de\(\{1, 2, 3, 4\}\). De manera más general, dado un grupo\(G\) que actúa sobre un conjunto\(S\), la órbita de\(G\) determinado por un elemento\(x\) de\(S\) es el conjunto

\(\{σ(x)|σ ∈ G\}\),

y se denota por\(Gx\). En el Problema 287 era posible tener\(Gx = Gy\). De hecho en ese problema,\(Gx = Gy\) para cada\(y\) en\(Gx\).

Ejercicio\(289\)

Supongamos que un grupo actúa sobre un conjunto\(S\). ¿Podría un elemento\(S\) estar en dos órbitas diferentes? (Di por qué o por qué no.) (Pista).

El problema 289 casi completa la prueba del siguiente teorema.

Teorema\(\PageIndex{1}\)

Supongamos que un grupo actúa sobre un conjunto\(S\). Las órbitas\(G\) forman una partición de\(S\).

Probablemente vale la pena señalar que este teorema nos dice que la órbita\(Gx\) es también la órbita\(Gy\) para cualquier elemento\(y\) de\(Gx\).

Ejercicio\(290\)

Completar la prueba del Teorema 9.

Observe que pensar en términos de órbitas en realidad esconde alguna información sobre la acción de nuestro grupo. Cuando calculamos el multiset de todos los resultados de actuar\(\{1, 2\}\) con los elementos de\(D_4\), obtuvimos un multiset de ocho elementos que contenía cada lado dos veces. Cuando calculamos el multiset de todos los resultados de actuar\(\{1, 3\}\) con los elementos de\(D_4\), obtuvimos un multiset de ocho elementos que contenía cada diagonal del cuadrado cuatro veces. Estos multisets nos recuerdan que estamos actuando sobre nuestros conjuntos de dos elementos con un grupo de ocho elementos. La multiórbita de\(G\) determinada por un elemento\(x\) de\(S\) es el multiset

\(\{σ(x)|σ ∈ G\}\),

y se denota por\(Gx_{\text{multi}}\).

Cuando usamos el principio del cociente para contar arreglos circulares de asientos o collares, dividimos un conjunto de listas de personas o cuentas en bloques de listas equivalentes. En el caso de sentar\(n\) gente alrededor de una mesa redonda, lo que hizo que dos listas fueran equivalentes fue, en retrospectiva, la acción del grupo de rotación\(C_n\). En el caso de encordar\(n\) cuentas en una cuerda para hacer un collar, lo que hizo que dos listas fueran equivalentes fue la acción del grupo diedro. Así los bloques de nuestras particiones eran órbitas del grupo de rotación o del grupo diedro, y estábamos contando el número de órbitas de la acción grupal. En el Problema 45, no pudimos aplicar el principio del cociente porque teníamos bloques de diferentes tamaños. No obstante, estos bloques seguían siendo órbitas de la acción del grupo\(D_4\). Y, a pesar de que las órbitas tienen diferentes tamaños, esperamos que cada órbita corresponda naturalmente a una multiórbita y que todas las multiórbitas tengan el mismo tamaño. Así, si tuviéramos una versión de la regla del cociente para una unión de multiconjuntos, podríamos esperar usarla para contar el número de multiórbitas.

Ejercicio\(291\)

1. Encuentra la órbita y multiórbita de\(D_4\) actuar sobre la coloración\(\{(1, R),(2, R),(3, B),(4, B)\}\), o, en notación estándar,\(RRBB\), de los vértices de un cuadrado.
2. ¿Cuántos elementos grupales mapean la coloración\(RRBB\) a sí mismo? ¿Cuál es la multiplicidad de\(RRBB\) en su multiórbita?
3. Encuentra la órbita y multiórbita de\(D_4\) actuar sobre la coloración\(\{(1, R),(2, B),(3, R),(4, B)\}\).
4. ¿Cuántos elementos del grupo envían la coloración\(RBRB\) a sí mismo? ¿Cuál es la multiplicidad de\(RBRB\) en su órbita?

Ejercicio\(292\)

1. Si\(G\) es un grupo, ¿con qué se\(\{τσ|τ ∈ G\}\) relaciona el conjunto\(G\)?
2. Usa esto para mostrar que\(y\) está en la multiórbita\(Gx_{\text{multi}}\) si y solo si\(Gx_{\text{multi}} = Gy_{\text{multi}}\).

El problema 292b nos dice que, cuando\(G\) actúa sobre\(S\), cada elemento\(x\) de\(S\) está en una y sólo una multiórbita. Dado que cada órbita es un subconjunto de una multiórbita y cada elemento\(x\) de\(S\) está en una y sólo una órbita, esto también nos dice que hay una biyección entre las órbitas de\(G\) y las multiórbitas de\(G\), de manera que tenemos el mismo número de órbitas que las multiórbitas.

Cuando un grupo actúa sobre un conjunto, se dice que un elemento de grupo fija un elemento de\(x ∈ S\) if\(σ(x) = x\). El conjunto de todos los elementos que fijan un elemento\(x\) se denota por\(\text{Fix}(x)\).

Ejercicio\(293\)

Supongamos que un grupo\(G\) actúa sobre un conjunto\(S\). ¿Qué tiene de especial el subconjunto\(\text{Fix}(x)\) para un elemento\(x\) de\(S\)?

\(\bullet\) Exercise \(294\)

Supongamos que un grupo\(G\) actúa sobre un conjunto\(S\). ¿Cuál es la relación de la multiplicidad de\(x ∈ S\) en su multiórbita y el tamaño de\(\text{Fix}(x)\)?

Ejercicio\(295\)

¿Qué se puede decir sobre las relaciones entre la multiplicidad de un elemento\(y\) en la multiórbita\(Gx_{\text{multi}}\) y las multiplicidades de otros elementos? Trate de usar esto para obtener una relación entre el tamaño de una órbita de\(G\) y el tamaño de\(G\). (Pista).

Sugerimos anteriormente que un principio de cociente para multiconjuntos podría resultar útil. El principio del cociente vino del principio de suma, y no tenemos un principio de suma para multiconjuntos. Tal principio diría que el tamaño de una unión de multiconjuntos disjuntos es la suma de sus tamaños. Todavía no hemos definido la unión de multiconjuntos o multiconjuntos disjuntos, porque hasta ahora no hemos necesitado las ideas. Definimos la unión de dos multiconjuntos\(S\) y\(T\) ser el multiconjunto en el que la multiplicidad de un elemento\(x\) es el máximo ² de la multiplicidad de\(x\) in\(S\) y su multiplicidad en\(T\). De igual manera, la unión de una familia de multiconjuntos se define definiendo la multiplicidad de un elemento\(x\) para que sea el máximo de sus multiplicidades en los miembros de la familia. Se dice que dos multiconjuntos son disjuntos si ningún elemento es miembro de ambos, es decir, si ningún elemento tiene multiplicidad uno o más en ambos. Dado que el tamaño de un multiconjunto es la suma de las multiplicidades de sus miembros, inmediatamente obtenemos el principio de suma para multiconjuntos.

El tamaño de una unión de multiconjuntos disjuntos es la suma de sus tamaños.

Tomando los multisets todos para tener el mismo tamaño, obtenemos el principio del producto para multisets.

La unión de un conjunto de\(m\) multiconjuntos disjuntos, cada uno de tamaño\(n\) tiene tamaño\(mn\).

El principio de cociente para multiconjuntos sigue entonces inmediatamente.

Si un multiconjunto\(p\) -elemento es una unión de\(q\) multiconjuntos disjuntos, cada uno de tamaño\(r\), entonces\(q = p/r\).

\(\bullet\) Exercise \(296\)

¿Cómo se\(S\) relaciona el tamaño de la unión del conjunto de multiórbitas de un grupo\(G\) que actúa sobre un conjunto con el número de multiórbitas y el tamaño de\(G\)?

\(\bullet\) Exercise \(297\)

¿Cómo se\(S\) relaciona el tamaño de la unión del conjunto de multiórbitas de un grupo\(G\) que actúa sobre un conjunto con los números\(|\text{Fix}(x)|\)?

\(\bullet\) Exercise \(298\)

En Problemas 296 y 297 computaste el tamaño de la unión del conjunto de multiórbitas de un grupo\(G\) actuando sobre un conjunto de dos\(S\) maneras distintas, obteniendo dos expresiones distintas que deben ser iguales. Escribe la ecuación que dice que son iguales y resuelve para el número de multiórbitas, y por lo tanto el número de órbitas.

6.2.3: El teorema de Cauchy-Frobenius-Burnside

\(\bullet\) Exercise \(299\)

En el Problema 298 usted declaró y demostró un teorema que expresa el número de órbitas en términos del número de elementos de grupo que fijan cada elemento de\(S\). A menudo es más fácil encontrar el número de elementos fijados por un elemento de grupo dado que encontrar el número de elementos de grupo que fijan un elemento de\(S\).

1. Para ello, ¿cómo\(\sum_{x:x∈S} |\text{Fix}(x)|\) se relaciona la suma con el número de pares ordenados\((σ, x)\) (con\(σ ∈ G\) y\(x ∈ S\)) tal que\(σ\) fija\(x\)?
2. Dejar\(χ(σ)\) denotar el número de elementos de\(S\) fijo por\(σ\). ¿Cómo se puede calcular el número de pares ordenados\((σ, x)\) (con\(σ ∈ G\) y\(x ∈ S\)) de los que\(x\) se calculan las\(σ\) correcciones\(χ(σ)\)? (Está bien tener una suma en tu respuesta.)
3. ¿Qué te dice esto sobre el número de órbitas?

Ejercicio\(300\)

Un segundo cálculo del resultado del problema 299 se puede hacer de la siguiente manera.

1. a. dejar\(\hat{χ}(σ, x) = 1\) si\(σ(x) = x\) y dejar\(\hat{χ}(σ, x) = 0\) lo contrario. Observe que\(\hat{χ}\) es diferente al\(χ\) del problema anterior, porque es una función de dos variables. Utilice\(\hat{χ}\) para convertir la suma única en su respuesta al Problema 298 en una doble suma sobre elementos\(x\) de\(S\) y elementos\(σ\) de\(G\).
2. Invierta el orden de la suma anterior para convertirla en una sola suma que involucre la función\(χ\) dada por

\(χ(σ) =\)el número de elementos de la\(S\) izquierda fijado por\(σ\).

En Problema 299 diste una fórmula para el número de órbitas de un grupo\(G\) que actuaba sobre un set\(X\). Esta fórmula fue elaborada primero por Cauchy en el caso del grupo simétrico, y luego para grupos más generales por Frobenius. En su libro pionero sobre Teoría de Grupos, Burnside utilizó este resultado como lema, y aunque atribuyó el resultado a Cauchy y Frobenius en la primera edición de su libro, en ediciones posteriores, no lo hizo. Más tarde, otros matemáticos que utilizaron su libro nombraron al resultado “El lema de Burnside”, que es el nombre con el que todavía se le conoce más comúnmente. Aceptemos llamar a este resultado el Teorema de Cauchy-Frobenius-Burnside, o Teorema CFB para abreviar en un compromiso entre la precisión histórica y el uso común.

\(\rightarrow\) Exercise \(301\)

¿De cuántas maneras podemos encadenar cuatro cuentas rojas (idénticas), seis (idénticas) azules y siete (idénticas) verdes en un collar? (Pista).

\(\rightarrow\) Exercise \(302\)

Si tenemos un suministro ilimitado de cuentas rojas idénticas y cuentas azules idénticas, ¿\(17\)de cuántas maneras podemos encadenarlas en un collar?

\(\rightarrow\) Exercise \(303\)

Si tenemos cinco cuentas rojas (idénticas), cinco (idénticas) azules y cinco (idénticas) cuentas verdes, ¿de cuántas maneras podemos ensartarlas en un collar?

\(\rightarrow\) Exercise \(304\)

¿De cuántas maneras podemos pintar las caras de un cubo con seis colores diferentes, usando los seis?

Ejercicio\(305\)

¿De cuántas maneras podemos pintar las caras de un cubo con dos colores de pintura? ¿Y si se deben usar ambos colores? (Pista).

\(\rightarrow\) Exercise \(306\)

¿De cuántas maneras podemos colorear los bordes de un (regular)\((2n + 1)\) -gon libre para movernos en el plano (así que no se puede voltear) si usamos\(n\) tiempos rojos y\(n + 1\) tiempos azules? Si se trata de un número que has visto antes, identifícalo. (Pista).

\(\rightarrow \; *\) Exercise \(307\)

¿De cuántas maneras podemos colorear los bordes de un\((2n + 1)\) gon (regular) libremente para movernos en un espacio tridimensional para que\(n\) los bordes sean de color rojo y\(n + 1\) los bordes sean de color azul? Tu respuesta puede depender de si\(n\) es par o impar.

\(\rightarrow \; *\) Exercise \(308\)

(No inusualmente duro para alguien que ha trabajado en polinomios cromáticos.) ¿Cuántos colores diferentes adecuados con cuatro colores hay de los vértices de una gráfica que es un ciclo en cinco vértices? (Si obtenemos una coloración rotando o volteando otra, no son realmente diferentes).

\(\rightarrow \; *\) Exercise \(309\)

¿Cuántos colorantes adecuados diferentes con cuatro colores hay de la gráfica en la Figura 6.2.3? Dos gráficas son iguales si podemos volver a dibujar una de las gráficas, sin cambiar el conjunto de vértices o el conjunto de bordes, para que sea idéntica a la otra. Esto equivale a permutar los vértices de alguna manera para que cuando aplicamos la permutación a los extremos de los bordes para obtener un nuevo conjunto de aristas, el nuevo conjunto de aristas sea igual al anterior. Tal permutación se llama automorfismo de la gráfica. Así dos colorantes son diferentes si no hay automorfismo de la gráfica que lleva una a la otra. (Pista).

Figura\(\PageIndex{3}\): Gráfica sobre seis vértices. (Copyright; autor vía fuente)

Notas

1. El lector que haya estudiado el Apéndice A reconocerá que este conjunto de pares ordenados es la relación de la función\(f\), pero no necesitaremos hacer ninguna referencia específica a la idea de una relación en lo que sigue.

2. Elegimos el máximo en lugar de la suma para que la unión de conjuntos sea un caso especial de la unión de multiconjuntos.