6.1: Grupos de permutación

Comenzamos por estudiar los tipos de permutaciones que surgen en situaciones en las que hemos utilizado el principio del cociente en el pasado.

6.1.1: Las rotaciones de un cuadrado

Figura\(\PageIndex{1}\): Los cuatro posibles resultados de rotar un cuadrado pero mantener su ubicación. (Copyright; autor vía fuente)

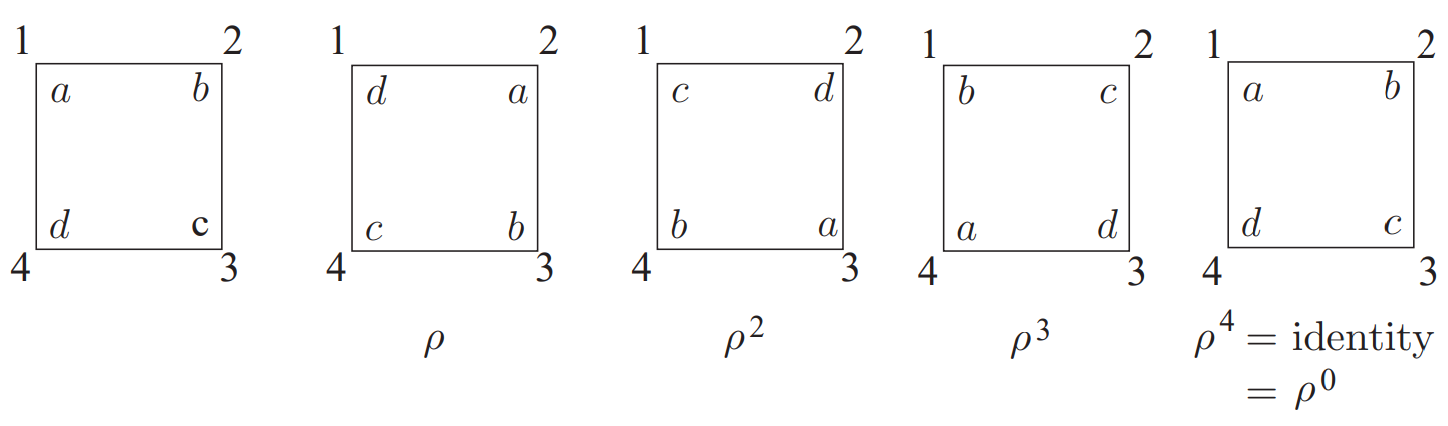
En la Figura 6.1.1 mostramos un cuadrado con sus cuatro vértices etiquetados\(a\),\(b\),\(c\), y\(d\). También hemos etiquetado los puntos en el plano donde cada uno de estos vértices cae con la etiqueta\(1\),\(2\),\(3\), o\(4\). Entonces hemos mostrado el efecto de girar el cuadrado en sentido horario a través de\(90\)\(180\),\(270\), y\(360\) grados (que es lo mismo que rotar a través de\(0\) grados).

Debajo de cada uno de los cuadrados girados hemos nombrado a la función que lleva a cabo la rotación. Usamos\(ρ\), la letra griega pronunciada “fila”, para representar un\(90\) grado de rotación en el sentido de las agujas del reloj. Solemos\(ρ^2\) representar rotaciones de dos\(90\) grados, y así sucesivamente. Podemos pensar en la función\(ρ\) como una función en el conjunto de cuatro elementos ¹\(\{1, 2, 3, 4\}\). En particular, para cualquier función\(\varphi\) (la letra griega phi, generalmente pronunciada “fee”, pero a veces “fie”) desde el plano de regreso a sí misma que pueda mover el cuadrado alrededor pero por lo demás lo deja en la misma ubicación, dejamos\(\varphi (i)\) ser la etiqueta del lugar donde el vértice anteriormente en posición i se encuentra ahora. Así\(ρ(1) = 2\),\(ρ(2) = 3\),\(ρ(3) = 4\) y\(ρ(4) = 1\). Observe que\(ρ\) es una permutación en el set\(\{1, 2, 3, 4\}\).

\(\bullet\) Exercise \(248\)

La composición\(f \circ g\) de dos funciones\(f\) y\(g\) se define por\(f \circ g(x) = f(g(x))\). ¿Es\(ρ^3\) la composición de\(ρ\) y\(ρ^2\)? ¿Depende la respuesta del orden en que escribamos\(ρ\) y\(ρ^2\)? ¿Cómo se\(ρ^2\) relaciona con\(ρ\)?

\(\bullet\) Exercise \(249\)

¿La composición de dos permutaciones es siempre una permutación?

En Problema 248 ves que podemos pensar en\(ρ^2 \circ ρ\) como el resultado de primero rotar por\(90\) grados y luego por otros\(180\) grados. Es decir, la composición de dos rotaciones es lo mismo que primero hacer una y luego hacer la otra. Por supuesto, no hay nada especial en\(90\) grados y\(180\) grados. Siempre y cuando primero hagamos una rotación a través de un múltiplo de\(90\) grados y luego otra rotación a través de un múltiplo de\(90\) grados, la composición de estas rotaciones es una rotación a través de un múltiplo de\(90\) grados.

Si primero giramos por\(90\) grados y luego por\(270\) grados entonces hemos girado por\(360\) grados, lo que no hace nada visible para el cuadrado. Así decimos que esa\(ρ^4\) es la “función de identidad”. En general, la función de identidad en un conjunto\(S\), denotada por\(ι\) (la letra griega iota, pronunciada eye-oh-ta) es la función que lleva cada elemento del conjunto a sí mismo. En símbolos,\(ι(x) = x\) para cada\(x\) en\(S\). Por supuesto, la función de identidad en un conjunto es una permutación de ese conjunto.

6.1.2: Grupos de Permutaciones

\(\bullet\) Exercise \(250\)

Para cualquier función\(\varphi\) de un conjunto\(S\) a sí mismo, definimos\(\varphi^{n}\) (para enteros no negativos n) inductivamente por\(\varphi^{0} = ι\) y\(\varphi^{n} = \varphi^{n−1} ◦ \varphi \) para cada entero positivo\(n\). Si\(\varphi\) es una permutación, ¿es\(\varphi^{n}\) una permutación? En base a tu experiencia con pruebas inductivas previas, ¿qué esperas\(\varphi^{n} ◦ \varphi^{m}\) ser? ¿Qué esperas\((\varphi^{m})^n\) ser? No hay necesidad de probar que estas dos últimas respuestas son correctas, pues en efecto ya lo has hecho en el Capítulo 2.

\(\bullet\) Exercise \(251\)

Si realizamos la composición\(ι ◦ \varphi\) para alguna función\(\varphi\) desde\(S\) hasta\(S\), ¿qué función obtenemos? ¿Y si realizamos la composición\(\varphi ◦ ι\)?

Lo que has observado sobre iota en el Problema 251 se llama la propiedad de identidad de iota. En el contexto de las permutaciones, la gente suele llamar a la función\(ι\) “la identidad” en lugar de llamarla “iota”.

Dado que rotar primero por\(90\) grados y luego por\(270\) grados tiene el mismo efecto que no hacer nada, podemos pensar en la rotación de\(270\) grados como deshacer lo que hace la rotación de\(90\) grados. Por ello, decimos que en las rotaciones del cuadrado,\(ρ^3\) es la “inversa” de\(ρ\). En general, una función\(\varphi: T → S\) se llama inversa de una función\(σ: S → T\) (\(σ\)es la letra griega minúscula sigma) if\(\varphi ◦ σ = σ ◦ \varphi = ι\). Para una introducción más lenta a las inversas y la práctica con ellas, véase la Sección A.1.3 en el Apéndice A. Dado que una permutación es una biyección, tiene una inversa única, como en la Sección A.1.3 del Apéndice A. Y como la inversa de una biyección es una biyección (nuevamente, como en el Apéndice), la inversa de una permutación es una permutación.

Usamos\(\varphi^{−1}\) para denotar la inversa de la permutación\(\varphi\). Hemos visto que las rotaciones del cuadrado son funciones que devuelven el cuadrado a su ubicación original pero pueden mover los vértices a diferentes lugares. De esta manera, creamos permutaciones de los vértices del cuadrado. Hemos observado tres propiedades importantes de estas permutaciones.

• (Propiedad de identidad) Estas permutaciones incluyen la permutación de identidad.
• (Propiedad inversa) Siempre que estas permutaciones incluyan\(\varphi\), también incluyen\(\varphi^{−1}\).
• (Propiedad de Cierre) Siempre que estas permutaciones incluyan\(\varphi\) y\(σ\), también incluyan\(\varphi ◦ σ\).

Un conjunto de permutaciones con estas tres propiedades se denomina grupo de permutaciones ² o grupo de permutaciones. Llamamos al grupo de permutaciones correspondientes a rotaciones del cuadrado el grupo de rotación del cuadrado. Hay un grupo de rotación similar con\(n\) elementos para cualquier\(n\) -gon regular.

\(\bullet\) Exercise \(252\)

Si\(f: S → T\),\(g: T → X\), y\(h: X → Y\),\(h ◦ (g ◦ f) = (h ◦ g) ◦ f\) ¿es? ¿Qué dice esto sobre el estatus del derecho asociativo\(ρ ◦ (σ ◦ \varphi) = (ρ ◦ σ) ◦ \varphi\) en un grupo de permutaciones?

\(\bullet\) Exercise \(253\)

1. ¿Cómo debemos definir\(\varphi^{−n}\) para un elemento\(\varphi\) de un grupo de permutación? (Pista).
2. ¿Las dos reglas estándar para exponentes\(a^ma^n = a^{m+n}\) y\((a^m)^n = a^{mn}\) aún se mantendrán en un grupo si uno o más de los exponentes pueden ser negativos? (Aún no se requiere comprobante.)
3. Demostrar que\(\varphi^{−m})^n = \varphi^{−mn}\) cuando\(m\) y\(n\) son no negativos es diferente de probar que\(\varphi^m)^{−n} = \varphi^{−mn}\) cuando\(m\) y no\(n\) son negativos. Hacer una lista de todas esas fórmulas que necesitaríamos probar para probar que las reglas de exponentes de la Parte 253b sí se mantienen para todos los no negativos y negativos\(m\) y\(n\).
4. Si las reglas se mantienen, dé suficiente prueba para demostrar que sabe cómo hacerlo; de lo contrario, dé un contraejemplo.

\(\bullet\) Exercise \(254\)

Si un conjunto finito de permutaciones satisface la propiedad de cierre ¿es un grupo de permutaciones? (Pista).

\(\bullet\) Exercise \(255\)

Existen movimientos geométricos tridimensionales del cuadrado que lo devuelven a su ubicación original pero mueven algunos de los vértices a otras posiciones. Por ejemplo, si volteamos el cuadrado alrededor de una diagonal, la mayor parte se mueve fuera del plano durante el volteo, pero el cuadrado termina en la misma ubicación. Dibuje una figura como la Figura 6.1.1 que muestre todos los resultados posibles de dichos movimientos, incluyendo los que se muestran en la Figura 6.1.1. ¿Las permutaciones correspondientes forman un grupo?

Ejercicio\(256\)

Dejar\(σ\) y\(\varphi\) ser permutaciones.

1. ¿Por qué debe\(σ ◦ \varphi\) tener una inversa?
2. ¿Es\((σ ◦ \varphi)^{−1} = σ^{−1} \varphi^{−1}\)? (Demostrar o dar un contraejemplo.) (Pista).
3. ¿Es\((σ ◦ \varphi)^{−1} = \varphi^{−1} σ^{−1}\)? (Demostrar o dar un contraejemplo.)

\(\bullet\) Exercise \(257\)

Explique por qué el conjunto de todas las permutaciones de cuatro elementos es un grupo de permutación. ¿Cuántos elementos tiene este grupo? A este grupo se le llama el grupo simétrico en cuatro letras y se denota con\(S_4\).

6.1.3: El Grupo Simétrico

En general, el conjunto de todas las permutaciones de un conjunto\(n\) -elemento es un grupo. Se llama el grupo simétrico en\(n\) letras. No tenemos buenas descripciones geométricas (como rotaciones) para todos sus elementos, y sería inconveniente tener que escribir algo como “Let\(σ(1) = 3\),,\(σ(2) = 1\)\(σ(3) = 4\), y\(σ(4) = 1\)” cada vez que necesitamos introducir una nueva permutación. Introducimos una nueva notación para las permutaciones que nos permite denotarlas de manera razonablemente compacta y componerlas razonablemente rápido. Si\(σ\) es la permutación de\(\{1, 2, 3, 4\}\) dada por\(σ(1) = 3\),\(σ(2) = 1\),\(σ(3) = 4\) y\(σ(4) = 2\), escribimos

\[σ = \binom{1 \; 2 \; 3 \; 4}{3 \; 1 \; 4 \; 2} .\]

Llamamos a esta notación la notación de dos filas para las permutaciones. En la notación de dos filas para una permutación de\(\{a_1, a_2, . . . , a_n\}\), escribimos los números\(a_1\) a través\(a_n\) en una fila y\(σ(a_1)\) escribimos\(σ(a_n)\) en una fila justo debajo, encerrando ambas filas entre paréntesis. Observe que

\[\binom{1 \; 2 \; 3 \; 4}{3 \; 1 \; 4 \; 2} = \binom{2 \; 1 \; 4 \; 3}{1 \; 3 \; 2 \; 4},\]

aunque rara vez se utiliza el segundo orden de las columnas.

Si\(\varphi\) es dado por

\[\varphi = \binom{1 \; 2 \; 3 \; 4}{4 \; 1 \; 2 \; 3}\],

entonces, aplicando la definición de composición de funciones, podemos calcular σ ◦ φ como se muestra en la Figura 6.2.

Figura\(\PageIndex{2}\): Cómo multiplicar permutaciones en notación de dos filas. (Copyright; autor vía fuente)

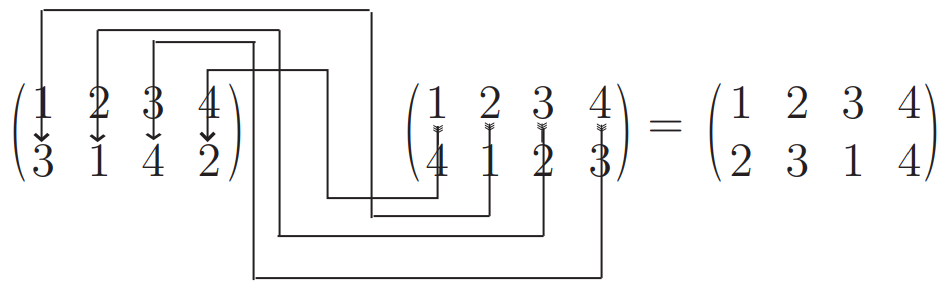
Normalmente no ponemos el círculo entre dos permutaciones en notación de dos filas cuando las estamos componiendo, y nos referimos a la operación como multiplicar las permutaciones, o como producto de las permutaciones. Para ver cómo la Figura 6.1.2 ilustra la composición, observe que la flecha que comienza\(1\) en en\(\varphi\) va a\(4\). Entonces desde el\(4\) adentro\(\varphi\) va a la\(4\) entrada\(σ\) y luego a\(2\). Esto ilustra eso\(\varphi(1) = 4\) y\(σ(4) = 2\), así que eso\(σ(\varphi(1)) = 2\).

Ejercicio\(258\)

Para práctica, cómputos\(\binom{1 \; 2 \; 3 \; 4 \; 5}{3 \; 4 \; 1 \; 5 \; 2} = \binom{1 \; 2 \; 3 \; 4 \; 5}{4 \; 3 \; 5 \; 1 \; 2} .\)

6.1.4: El Grupo Diedro

Se encontraron cuatro permutaciones que corresponden a rotaciones del cuadrado. En Problema 255 encontraste cuatro permutaciones que corresponden a volteretas del cuadrado en el espacio. Un volteo fija los vértices en los lugares etiquetados\(1\)\(3\) e intercambia los vértices en los lugares etiquetados\(2\) y\(4\). Denotémoslo por\(\varphi_{1|3}\). Un volteo fija los vértices en las posiciones etiquetadas\(2\)\(4\) e intercambia los de las posiciones etiquetadas\(1\) y\(3\). Denotémoslo por\(\varphi_{2|4}\). Un volteo intercambia los vértices en los lugares etiquetados\(1\)\(2\) y también intercambia los de los lugares etiquetados\(3\) y\(4\). Denotémoslo por\(\varphi_{12|34}\). El cuarto flip intercambia los vértices en los lugares etiquetados\(1\)\(4\) e intercambia los de los lugares etiquetados\(2\) y\(3\). Denotémoslo por\(\varphi_{14|23}\). Observe que\(\varphi_{1|3}\) es una permutación que lleva el vértice en su lugar\(1\) al vértice en su lugar\(1\) y el vértice en su lugar\(3\) al vértice en su lugar\(3\), mientras que\(\varphi_{12|34}\) es una permutación que toma el borde entre lugares\(1\) y\(2\) al borde entre lugares\(2\) y\(1\) (que es el mismo borde) y toma el borde entre lugares\(3\) y\(4\) al borde entre lugares\(4\) y\(3\) (que es el mismo borde). Esto debería ayudar a explicar la similitud en la notación para los dos tipos diferentes de volteretas.

\(\bullet\) Exercise \(259\)

Anote la notación de dos filas para\(ρ^3\),\(\varphi_{2|4}\),\(\varphi_{12|34}\) y\(\varphi_{2|4} ◦ \varphi_{12|34}\). Recuerde que\(σ(i)\) significa la posición donde el vértice que se originó en posición\(i\) es después de aplicar\(σ\).

Ejercicio\(260\)

(Puede que ya hayas hecho este problema en Problema 255, en cuyo caso no necesitas volver a hacerlo!) En el Problema 255, si un movimiento rígido en el espacio tridimensional devuelve el cuadrado a su ubicación original, ¿en cuántos lugares puede aterrizar el vértice número uno? Una vez que se decide la ubicación del vértice número uno, ¿cuántas ubicaciones posibles hay para el vértice dos? Una vez que se deciden las ubicaciones del vértice uno y el vértice dos, ¿cuántas ubicaciones hay para el vértice tres? Responde la misma pregunta para el vértice cuatro. ¿Qué dice esto sobre la relación entre las cuatro rotaciones y cuatro volteretas descritas justo antes del Problema 259 y las permutaciones que describió en el Problema 255?

Las cuatro rotaciones y cuatro volteretas del cuadrado descritas antes del Problema 259 forman un grupo llamado grupo diedro del cuadrado. A veces el grupo se denota\(D_8\) porque tiene ocho elementos, y a veces el grupo se denota por ¡\(D_4\)porque trata de cuatro vértices! Aceptemos usar la notación\(D_4\) para el grupo diedro del cuadrado. Existe un grupo diedro similar, denotado por\(D_n\), de todos los movimientos rígidos del espacio tridimensional que devuelven un\(n\) -gon regular a su ubicación original (pero podría poner los vértices en diferentes lugares).

Ejercicio\(261\)

Otra visión del grupo diedro de la plaza es que es el grupo de todas las funciones conservadoras de distancia, también llamadas isometrías, de un cuadrado a sí mismo. Observe que una isometría debe ser una biyección. Cualquier movimiento rígido del cuadrado conserva las distancias entre todos los puntos del cuadrado. Sin embargo, es concebible que pueda haber algunas isometrías que no surjan de movimientos rígidos. (Veremos algunos más adelante en el caso de un cubo.) Demostrar que hay exactamente ocho isometrías (funciones de preservación de distancia) de un cuadrado a sí mismo. (Pista).

Ejercicio\(262\)

¿Cuántos elementos tiene el grupo\(D_n\)? Demuestre que está en lo correcto.

Ejercicio\(263\)

En la Figura 6.1.3 mostramos un cubo con las posiciones de sus vértices y caras etiquetadas. Al igual que con los movimientos de la plaza, dejamos que\(\varphi(x)\) sea la etiqueta del lugar donde el vértice anteriormente en posición\(x\) está ahora.

Figura\(\PageIndex{3}\): Un cubo con las posiciones de sus vértices y caras etiquetadas. (Copyright; autor vía fuente)

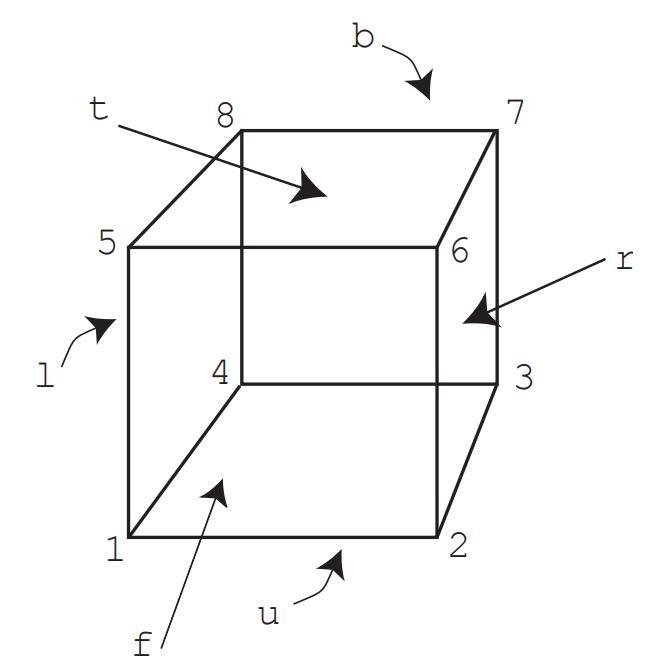
1. Escribe en notación de dos filas la permutación\(ρ\) de los vértices que corresponde a rotar los\(90\) grados del cubo alrededor de un eje vertical a través de las caras\(t\) (para arriba) y\(u\) (para debajo). (Rota de manera diestra alrededor de este eje, lo que significa que el vértice\(6\) va hacia atrás y el vértice\(8\) llega al frente).
2. Escribe en notación de dos filas la permutación\(\varphi\) que gira los\(120\) grados del cubo alrededor de la diagonal de vértice\(1\) a vértice\(7\) y lleva vértice\(8\) a vértice\(6\).
3. Calcula la notación de dos filas para\(ρ ◦ \varphi\).
4. ¿La permutación es\(ρ ◦ \varphi\) una rotación del cubo alrededor de algún eje? Si es así, digamos cuál es el eje y cuántos grados giramos alrededor del eje. Si no\(ρ ◦ \varphi\) es una rotación, dar una descripción geométrica de la misma.

\(\rightarrow \; \cdot\) Exercise \(264\)

¿Cuántas permutaciones hay en el grupo\(R\)? \(R\)a veces se llama el “grupo de rotación” del cubo. ¿Puedes justificar esto? (Pista).

Ejercicio\(265\)

Al igual que con una figura bidimensional, es posible hablar de isometrías de una figura tridimensional. Estas son funciones que preservan la distancia de la figura a sí misma. La función que refleja el cubo en la Figura 6.1.3 a través de un plano a medio camino entre la cara inferior y la cara superior intercambia los vértices\(1\)\(2\)\(3\) y\(5\)\(6\)\(7\), y,\(4\) y y\(8\) del cubo. Esta función preserva las distancias entre puntos en el cubo. Sin embargo, no se puede lograr mediante un movimiento rígido del cubo porque un movimiento rígido que lleva vértice\(1\) a vértice\(5\), vértice\(2\) a vértice\(6\), vértice\(3\) a vértice\(7\) y vértice\(4\) a vértice no\(8\) devolvería el cubo a su original ubicación; más bien pondría la parte inferior del cubo donde anteriormente estaba su parte superior y pondría el resto del cubo por encima de ese cuadrado en lugar de debajo de él.

1. ¿Cuántos elementos hay en el grupo de permutaciones de\([8]\) que corresponden a isometrías del cubo? (Pista).
2. ¿Toda permutación de\([8]\) eso corresponde a una isometría, ya sea una rotación o una reflexión? (Pista).

6.1.5: Mesas de Grupo (Opcional)

Siempre podemos averiguar la composición de dos permutaciones del mismo conjunto usando la definición de composición, pero si vamos a trabajar con un grupo de permutación dado una y otra vez, vale la pena hacer los cálculos una vez y grabarlos en una tabla. Por ejemplo, el grupo de rotaciones del cuadrado se puede representar como en el Cuadro 6.1.1. Listamos los elementos de nuestro grupo, con la identidad primero, a través de la parte superior de la tabla y abajo del lado izquierdo de la tabla, usando el mismo orden ambas veces. Después, en la fila etiquetada por el elemento group\(σ\) y la columna etiquetada por el elemento group\(\varphi\), escribimos la composición\(σ ◦ \varphi\), expresada en términos de los elementos que hemos enumerado en la parte superior y en el lado izquierdo. Dado que un grupo de permutaciones se cierra bajo composición, el resultado siempre\(σ ◦ \varphi\) será expresable como uno de estos elementos.

Cuadro 6.1.1: La Tabla de Grupos para las Rotaciones de un Cuadrado
\(\circ\)	\(ι\)	\(ρ\)	\(ρ^2\)	\(ρ^3\)
\ (\ circ\)” alcance="fila">\(ι\)	\ (ι\) ">\(ι\)	\ (ρ\) ">\(ρ\)	\ (ρ^2\) ">\(ρ^2\)	\ (ρ^3\) ">\(ρ^3\)
\ (\ circ\)” alcance="fila">\(ρ\)	\ (ι\) ">\(ρ\)	\ (ρ\) ">\(ρ^2\)	\ (ρ^2\) ">\(ρ^3\)	\ (ρ^3\) ">\(ι\)
\ (\ circ\)” alcance="fila">\(ρ^2\)	\ (ι\) ">\(ρ^2\)	\ (ρ\) ">\(ρ^3\)	\ (ρ^2\) ">\(ι\)	\ (ρ^3\) ">\(ρ\)
\ (\ circ\)” alcance="fila">\(ρ^3\)	\ (ι\) ">\(ρ^3\)	\ (ρ\) ">\(ι\)	\ (ρ^2\) ">\(ρ\)	\ (ρ^3\) ">\(ρ^2\)

Ejercicio\(266\)

En la Tabla 6.1.1, todas las entradas en una fila (sin incluir la primera entrada, la que está a la izquierda de la línea) son diferentes. ¿Será esto cierto en alguna tabla de grupo para un grupo de permutación? ¿Por qué o por qué no? También, en la Tabla 6.1.1, todas las entradas de una columna (sin incluir la primera entrada, la que está por encima de la línea) son diferentes. ¿Será esto cierto en alguna tabla de grupo para un grupo de permutación? ¿Por qué o por qué no?

Ejercicio\(267\)

En la Tabla 6.1.1, cada elemento del grupo aparece en cada fila (aunque no incluya el primer elemento, el anterior a la línea). ¿Será esto cierto en alguna tabla de grupo para un grupo de permutación? ¿Por qué o por qué no? También en la Tabla 6.1.1 cada elemento del grupo aparece en cada columna (aunque no incluya la primera entrada, la anterior a la línea). ¿Será esto cierto en alguna tabla de grupo para un grupo de permutación? ¿Por qué o por qué no?

\(\bullet\) Exercise \(268\)

Anote la tabla de grupos para el grupo diedro\(D_4\). Use la\(\varphi\) notación descrita anteriormente para denotar los volteos. (Consejos: Parte de la tabla ya ha sido anotada. ¿Necesitarás pensar mucho para anotar la última fila? ¿Necesitarás pensar mucho para anotar la última columna? Cuando multiplicas un producto como\(\varphi_{1|3} ◦ ρ\) recuerda que\(\varphi_{1|3}\) definimos que es el flip que fija el vértice en posición\(1\) y el vértice en posición\(3\), no el que fija el vértice en el cuadrado etiquetado\(1\) y el vértice en el cuadrado etiquetado\(3\).)

Puede notar que la ley asociativa, la propiedad de identidad y la propiedad inversa son tres de las reglas más importantes que utilizamos para reagrupar paréntesis en expresiones algebraicas al resolver ecuaciones. Hay una propiedad que aún no hemos mencionado, la ley conmutativa, que diría eso\(σ ◦ \varphi = \varphi ◦ σ\). Es fácil ver por la tabla de grupos del grupo de rotación de un cuadrado que satisface la ley conmutativa.

Ejercicio\(269\)

¿Se mantiene la ley conmutativa en todos los grupos de permutación?

6.1.6: Subgrupos

Hemos visto que el grupo diedro\(D_4\) contiene una copia del grupo de rotaciones de la plaza. Cuando un grupo\(G\) de permutaciones de un conjunto\(S\) es un subconjunto de otro grupo\(G_0\) de permutaciones de\(S\), decimos que\(G\) es un subgrupo de\(G_0\).

\(\bullet\) Exercise \(270\)

Encuentra todos los subgrupos del grupo\(D_4\) y explica por qué tu lista está completa. (Pista).

Ejercicio\(271\)

¿Se pueden encontrar subgrupos del grupo simétrico\(S_4\) con dos elementos? ¿Tres elementos? ¿Cuatro elementos? ¿Seis elementos? (Para cada respuesta positiva, describa un subgrupo. Por cada respuesta negativa, explique por qué no.)

6.1.7: La descomposición del ciclo de una permutación

El dígrafo de una permutación nos da una buena manera de pensarlo. Observe que el producto en la Figura 6.1.2 es\(\binom{1 \;2 \;3\; 4}{2\; 3\; 1\; 4}\). Hemos dibujado la gráfica dirigida de esta permutación en la Figura 6.1.4.

Figura\(\PageIndex{4}\): La gráfica dirigida de una permutación. (Copyright; autor vía fuente)

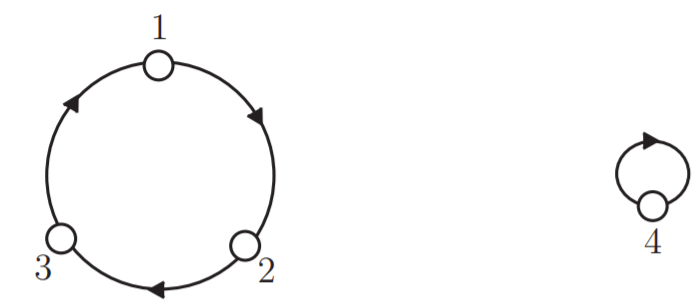
Se ve que la gráfica tiene dos ciclos dirigidos, el más bien trivial con vértice\(4\) apuntando a sí mismo, y el no trivial con vértice\(1\) apuntando a vértice\(2\) apuntando a vértice\(3\) que apunta de nuevo a vértice\(1\). Una permutación se llama ciclo si su dígrafo consiste exactamente en un ciclo. Así\(\binom{1\; 2\; 3}{2\; 3\; 1}\) es un ciclo pero no\(\binom{1 \;2 \;3 \;4}{2\; 3\; 1\; 4}\) es un ciclo por nuestra definición. Escribimos\((1\; 2\; 3)\) o\((2\; 3\; 1)\) o\((3\; 1\; 2)\) para estar de pie para el ciclo\(σ = \binom{1\; 2\; 3}{2\; 3\; 1}\).

También podemos describir los ciclos de otra manera. Un ciclo de la permutación\(σ\) es una lista\((i σ(i) σ^2 (i) . . . σ^n (i))\) que no tiene elementos repetidos mientras que la lista\((i σ(i) σ^2 (i) . . . σ^n (i) σ^{n+1}(i))\) sí tiene elementos repetidos.

Ejercicio\(272\)

Si la lista\((i σ(i) σ^2 (i) . . . σ^n (i))\) no tiene elementos repetidos pero la lista\((i σ(i) σ^2 (i) . . . σ^n (i) σ^{n+1}(i))\) sí tiene elementos repetidos, entonces ¿qué es\(σ^{n+1}(i)\)? (Pista).

Decimos que\(σ^j (i)\) es un elemento del ciclo\((i σ(i) σ^2 (i) . . . σ^n (i))\). Observe que el\(j = 0\) medio de caso\(i\) es un elemento del ciclo. Obsérvese también que si\(j > n\)\(σ^j (i) = σ^{j−n−1} (i)\),, así los distintos elementos del ciclo son\(i\),\(σ(i)\),\(σ^2 (i)\), a través\(σ^n (i)\). Pensamos que el ciclo\((i σ(i) σ^2 (i) . . . σ^n (i))\) representa la permutación\(σ\) restringida al conjunto de elementos del ciclo. Decimos que los ciclos\((i σ(i) σ^2 (i) . . . σ^n (i))\) y\((j σ(j) σ^2(j) ... σ^n(j))\) son equivalentes si hay un entero\(k\) tal que\(j = σ^k (i)\).

\(\bullet\) Exercise \(273\)

Encuentra los ciclos de las permutaciones\(ρ\),\(\varphi_{1|3}\) y\(\varphi_{12|34}\) en el grupo\(D_4\).

Ejercicio\(274\)

Encuentra los ciclos de la permutación.

\(\binom{1\; 2\; 3\; 4\; 5\; 6\; 7\; 8\; 9}{3\; 4\; 6\; 2\; 9\; 7\; 1\; 5\; 8}\)

Ejercicio\(275\)

Si dos ciclos de σ tienen un elemento en común, ¿qué podemos decir de ellos?

El problema 275 lleva casi de inmediato al siguiente teorema.

Teorema\(\PageIndex{1}\)

Para cada permutación\(σ\) de un conjunto\(S\), hay una partición única de\(S\) cada uno de cuyos bloques es el conjunto de elementos de un ciclo de\(σ\).

De manera más informal, podemos decir que cada permutación divide su dominio en ciclos disjuntos. Llamamos al conjunto de ciclos de una permutación la descomposición del ciclo de la permutación. Dado que los ciclos de una permutación nos\(σ\) dicen\(σ(x)\) para cada uno\(x\) en el dominio de\(σ\), la descomposición del ciclo de una permutación determina por completo la permutación. Usando nuestro lenguaje informal, podemos expresar esta idea en el siguiente corolario al Teorema 6.1.1

Corolario\(\PageIndex{1}\)

Cada partición de un conjunto\(S\) en ciclos determina una permutación única de\(S\).

Ejercicio\(276\)

Demostrar Teorema 6.1.1.

En Problemas 273 y 274 se encontraron las descomposiciones cíclicas de elementos típicos del grupo D4 y de la permutación

\(\binom{1\; 2\; 3\; 4\; 5\; 6\; 7\; 8\; 9}{3\; 4\; 6 \;2 \;9 \;7 \;1 \;5 \;8}\).

El grupo de todas las rotaciones de la plaza es simplemente el conjunto de las cuatro potencias del ciclo\(ρ = (1 \;2 \;3\; 4)\). Por esta razón, se le llama grupo cíclico ³ y a menudo denotado por\(C_4\). De manera similar, el grupo de rotación de un\(n\) -gon suele ser denotado por\(C_n\).

\(\rightarrow\) Exercise \(277\)

Escribir una recurrencia para el número\(c(k, n)\) de permutaciones de\([k]\) que tienen exactamente\(n\) ciclos, incluyendo\(1\) -ciclos. Utilízalo\(c(k, n)\) para escribir una tabla de\(k\) entre\(1\) e\(7\) inclusivo. ¿Se puede encontrar una relación entre\(c(k, n)\) y alguna de las otras familias de números especiales como coeficientes binomiales, números de Stirling, números de Lah, etc. que hemos estudiado? Si encuentra tal relación, demuestre que tiene razón. (Pista).

\(\rightarrow \; \cdot\) Exercise \(278\)

(Relevante al Apéndice C.) Una permutación\(σ\) se llama involución si\(σ^2 = ι\). Cuando se anota la descomposición del ciclo de una involución, ¿qué tienen de especial los ciclos?

Notas

1. Lo que estamos haciendo es restringir la rotación\(ρ\) al conjunto\(\{1, 2, 3, 4\}\)

2. El concepto de grupo de permutación es un caso especial del concepto de grupo que se estudia en álgebra abstracta. Cuando nos referimos a un grupo en lo que sigue, si sabes qué grupos son en el sentido más abstracto, puedes usar la palabra de esta manera. Si no conoces grupos en este sentido más abstracto, entonces puedes asumir que nos referimos a grupo de permutación cuando decimos grupo.

3. El grupo cíclico phrace se aplica en una situación más general (pero similar). A saber, el conjunto de todos los poderes de cualquier miembro de un grupo se llama grupo cíclico.