6.3: Teoría de la enumeración Pólya-Redfield
- Page ID
- 112648
George Pólya y Robert Redfield desarrollaron de forma independiente una teoría de generar funciones que describen la acción de un grupo\(G\) sobre los colorantes de un conjunto\(S\) por un conjunto\(T\) cuando conocemos la acción de\(G\) on\(S\). El trabajo de Pólya sobre el tema es muy accesible en su exposición, por lo que el tema ha llegado a ser conocido popularmente como teoría Pólya, aunque la teoría de Pólya-Redfield sería un nombre mejor. En esta sección, desarrollamos los elementos de esta teoría.
La idea de colorear un conjunto\(S\) tiene muchas aplicaciones. Por ejemplo, el conjunto\(S\) podría ser las posiciones en una molécula de hidrocarburo que están ocupadas por hidrógeno, y el grupo podría ser el grupo de simetrías espaciales de la molécula (es decir, el grupo de permutaciones de los átomos de la molécula que mueven la molécula alrededor de manera que en su posición final el molécula no puede distinguirse de la molécula original). Los colores podrían ser entonces radicales (incluido el hidrógeno mismo) que podríamos sustituir por cada posición de hidrógeno en la molécula. Entonces el número de órbitas de colorantes es el número de compuestos químicamente diferentes que podríamos crear usando estas sustituciones. 1
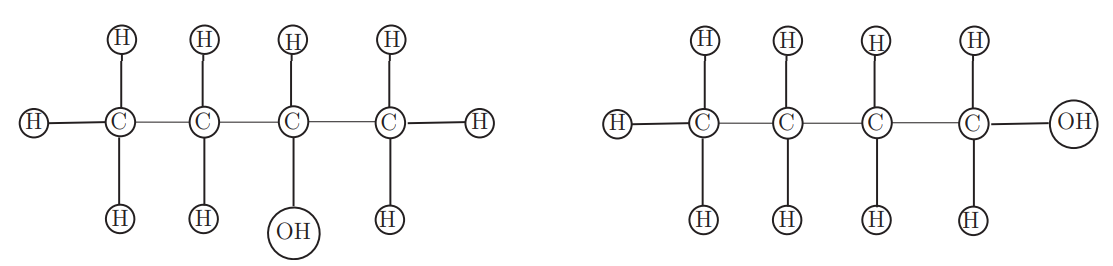
En la Figura 6.3.1 mostramos dos formas diferentes de sustituir el\(\text{OH}\) radical por un átomo de hidrógeno en el diagrama químico que dimos por butano en el Capítulo 2. Hemos coloreado un vértice de grado\(1\) con el radical\(\text{OH}\) y el resto con el átomo\(\text{H}\). Solo hay dos formas distintas de hacer esto, ya que el\(\text{OH}\) debe conectarse a un “extremo”\(\text{C}\) o a un “medio”\(\text{C}\). Esto demuestra que existen dos formas diferentes, llamadas isómeros del compuesto mostrado. Este compuesto se conoce como alcohol butílico.
Así que piensa intuitivamente en alguna “figura” que tiene lugares para ser coloreada. (Piense en las caras de un cubo, las cuentas de un collar, los círculos en los vértices de un\(n\) -gon, etc.) ¿Cómo podemos imaginarnos la coloración? Si numeramos los lugares a colorear, digamos\(1\)\(n\), entonces tenemos una forma estándar de representar nuestra coloración. Por ejemplo, si nuestros colores son el azul, el verde y el rojo, entonces\(BBGRRGBG\) describe una coloración típica de\(8\) tales lugares. A menos que los lugares estén de alguna manera “naturalmente” numerados, esta idea de una coloración impone una estructura que realmente no está ahí. Incluso si la estructura está ahí, visualizar nuestros colorantes de esta manera no “reúne” ninguna característica común de diferentes colorantes; simplemente estamos visualizando todos los colorantes posibles. Tenemos un grupo (pensarlo como simetrías de la figura que estás imaginando) que actúa sobre los lugares. Ese grupo actúa entonces de manera natural sobre los colorantes de los lugares y nos interesan las órbitas de los colorantes. Así queremos una imagen que reúna las características comunes de los colorantes en una órbita. Una forma de reunir similitudes de colores sería dejar que las letras que estamos usando como imágenes de colores viajen como lo hicimos con nuestras imágenes en el Capítulo 4; entonces nuestra imagen\(BBGRRGBG\) se convierte\(B^3G^3R^2\), así que nuestra imagen ahora registra simplemente cuántas veces usamos cada color. Piense en cómo definimos la acción de un grupo sobre los colorantes de un conjunto sobre el que actúa el grupo. Verás que actuar con un elemento de grupo no cambiará cuántas veces se usa cada color; simplemente mueve los colores a diferentes lugares. Así, la imagen que tenemos ahora de una coloración dada es una imagen igualmente apropiada para cada coloración en una órbita. Una pregunta natural para nosotros es “¿Cuántas órbitas tienen una imagen dada?”
Ejercicio\(310\)
Supongamos que dibujamos círculos idénticos en los vértices de un hexágono regular. Supongamos que coloreamos estos círculos con dos colores, rojo y azul.
- ¿De cuántas maneras podemos colorear el conjunto\(\{1, 2, 3, 4, 5, 6\}\) usando los colores rojo y azul?
- Estos colorantes son divididos en órbitas por la acción del grupo de rotación sobre el hexágono. Usando nuestra notación estándar, anota todas estas órbitas y observa cuántas órbitas tiene cada imagen, asumiendo que la imagen de una coloración es producto de variables de desplazamiento que representan los colores.
- Usando la función picture de la parte anterior, anote el enumerador de imágenes para las órbitas de coloraciones de los vértices de un hexágono bajo la acción del grupo de rotación.
En Problema 310c, vimos un enumerador de imágenes para imágenes de órbitas de la acción de un grupo sobre colorantes. Como anteriormente, nos preguntamos cuántas órbitas de los colorantes tienen alguna imagen dada. Podemos pensar en una función generadora multivariable en la que las letras que utilizamos para visualizar colores individuales son las variables, y el coeficiente de una imagen es el número de órbitas con esa imagen. Tal función generadora proporciona una respuesta a nuestra pregunta natural, y así es este tipo de función generadora la que buscaremos. Dado que el teorema de CFB fue nuestra herramienta principal para decir cuántas órbitas tenemos, tiene sentido pensar si el teorema de CFB tiene un análogo en términos de imágenes de órbitas.
6.3.1: El teorema del punto fijo de la órbita
\(\bullet\) Exercise \(311\)
Supongamos que ahora tenemos un grupo\(G\) actuando sobre un set y tenemos una función de imagen en ese conjunto con la característica adicional de que para cada órbita del grupo, todos sus elementos tienen la misma imagen. En esta circunstancia, definimos la imagen de una órbita o multiórbita para que sea la imagen de cualquiera de sus miembros. El enumerador de órbitas\(\text{Orb}(G, S)\) es la suma de las imágenes de las órbitas. (Tenga en cuenta que esto es lo mismo que la suma de las imágenes de las multiórbitas.) El enumerador de puntos fijos\(\text{Fix}(G, S)\) es la suma de las imágenes de cada uno de los puntos fijos de cada uno de los elementos de\(G\). Vamos a construir un análogo de función generadora del teorema de CFB. La idea principal de la prueba del teorema de CFB fue tratar de calcular de dos maneras diferentes el número de elementos (es decir, la suma de todas las multiplicidades de los elementos) en la unión de todas las multiórbitas de un grupo que actúa sobre un conjunto. Supongamos que en cambio intentamos calcular la suma de todas las imágenes de todos los elementos en la unión de las multiórbitas de un grupo que actúa sobre un conjunto. Al pensar en cómo se relaciona esta suma\(\text{Orb}(G, S)\) y\(\text{Fix}(G, S)\), encontrar un análogo del teorema de CFB que relacione a estos dos enumeradores. Estado y probar este teorema.
Llamaremos al teorema del Problema 311 Teorema de Órbita-Punto Fijo. Para aplicar el Teorema de Punto Fijo de Órbita, necesitamos algunos datos básicos sobre los enumeradores de imágenes.
\(\bullet\) Exercise \(312\)
Supongamos que\(P_1\) y\(P_2\) son funciones de imagen en conjuntos\(S_1\) y\(S_2\) en el sentido de la Sección 4.1.2. Definir\(P\)\(S_1 \times S_2\) por\(P(x_1, x_2) = P_1(x_1)P_2(x_2)\). ¿Cómo están\(E_{P_1}\)\(E_{P_1}\), y\(E_P\) relacionados? (¡Puede que ya hayas hecho este problema en otro contexto!)
\(\bullet\) Exercise 313
Supongamos que\(P_i\) es una función de imagen en un conjunto\(S_i\) para\(i = 1, . . . , k\). Definimos la imagen de una\(k\)\((x_1, x_2, . . . , x_k)\) -tupla como producto de las imágenes de sus elementos, i.e.
\(\hat{P}((x_1, x_2, . . . x_k)) = \prod_{i=1}^{k} P_i(x_i)\).
¿Cómo se\(x_i ∈ S_i\) relaciona el enumerador\(E_{\hat{P}}\) de imágenes del conjunto\(S_1 \times S_2 \times · · · \times S_k\) de\(k\) todo-tuplas con los enumeradores de imágenes de los conjuntos\(S_i\)? En el caso especial que\(S_i = S\) para todos\(i\) y\(P_i = P\) para todos\(i\), ¿qué es\(E_{\hat{P}} (S^k)\)?
\(\bullet\) Exercise \(314\)
Usa el Teorema de Punto Fijo de Órbita para determinar el Enumerador de Órbita para los colorantes, con dos colores (rojo y azul), de seis círculos colocados en los vértices de un hexágono el cual es libre de moverse en el plano. Compara los coeficientes del polinomio resultante con las diversas órbitas que encontraste en el Problema 310.
Ejercicio\(315\)
Encuentra la función generadora (en variables\(R\),\(B\)) para coloraciones de las caras de un cubo con dos colores (rojo y azul). ¿Qué te dice la función generadora sobre el número de formas de colorear el cubo (hasta el movimiento espacial) con varias combinaciones de los dos colores?
6.3.2: El teorema de Pólya-Redfield
El famoso teorema de enumeración de Pólya (y Redfield) trata de situaciones como las de Problemas 314 y 315 en las que queremos una función generadora para el conjunto de todos los colorantes un conjunto\(S\) usando un conjunto\(T\) de colores, donde la imagen de una coloración es producto del multiconjunto de colores que utiliza. Nuevamente estamos pensando en los colores como variables. El objetivo de la siguiente serie de problemas es analizar las soluciones a los Problemas 314 y 315 para ver lo que vieron Pólya y Redfield (aunque no lo vieron en esta notación o usando esta terminología).
\(\bullet\) Exercise \(316\)
En el Problema 314 tenemos cuatro tipos de elementos grupales: la identidad (que fija cada coloración), las rotaciones a través\(60\) o\(300\) grados, las rotaciones a través\(120\) y\(240\) grados, y la rotación a través de\(180\) grados. El enumerador de punto fijo para el grupo de rotación que actúa sobre los colorantes del hexágono es por definición la suma de los enumeradores de punto fijo de colorantes fijados por la identidad, de colorantes fijados por rotaciones\(60\) o\(300\) grados, de coloraciones fijadas por rotaciones de\(240\) grado\(120\) o grados, y de colorantes fijados por la rotación\(180\) de grados. En la medida en que aún no lo hayas hecho en un problema anterior, escribe cada uno de estos enumeradores (uno para cada tipo de permutación) individualmente y factoriza cada uno (sobre los enteros) de la manera más completa que puedas.
\(\bullet\) Exercise \(317\)
En Problema 315 tenemos cinco tipos diferentes de elementos grupales. Para cada tipo de elemento, en la medida en que aún no lo hayas hecho en un problema anterior, anota el enumerador de punto fijo para los elementos de ese tipo. Factorizar los enumeradores lo más completamente posible.
\(\bullet\) Exercise \(318\)
En el Problema 316, cada “tipo” de elemento de grupo tiene un “tipo” de estructura de ciclo. Por ejemplo, una rotación a través de\(180\) grados tiene tres ciclos de tamaño dos. ¿Qué tipo de descomposición de ciclo tiene una rotación\(60\) o\(300\) grados? ¿Qué tipo de descomposición de ciclo tiene una rotación\(120\) o\(240\) grados? Discutir la relación entre las estructuras cíclicas y los enumeradores factorizados de puntos fijos de las permutaciones en el Problema 316. Recordemos que dijimos que un grupo de permutaciones actúa sobre un conjunto\(S\) si, para cada miembro\(σ\) de\(G\) hay una permutación\(\overline{σ}\) de\(S\) tal que
\(\widehat{σ ◦ \varphi} = \hat{σ} ◦ \hat{\varphi}\)
para todos los miembros\(σ\) y\(\varphi\) de\(G\). Ya que\(σ\) es una permutación de\(S\),\(σ\) tiene una descomposición de ciclo como una permutación de\(S\) (así como cualquiera que sea su descomposición de ciclo es en el grupo de permutación original\(G\)).
\(\bullet\) Exercise \(319\)
En el Problema 317, cada “tipo” de elemento de grupo tiene una “especie” de descomposición del ciclo en la acción del grupo de rotación del cubo sobre las caras del cubo. Por ejemplo, una rotación del cubo a través de\(180\) grados alrededor de un eje vertical a través de los centros de las caras superior e inferior tiene dos ciclos de tamaño dos y dos ciclos de tamaño uno.
En la medida en que aún no lo hayas hecho en un problema anterior, contesta las siguientes preguntas. ¿Cuántas rotaciones de este tipo tiene el grupo? ¿Cuáles son los otros “tipos” de elementos grupales y cuáles son sus estructuras cíclicas? Discutir la relación entre la descomposición del ciclo y el enumerador factorizado en Problema 317.
\(\bullet\) Exercise \(320\)
La forma habitual de describir el teorema de la enumeración Pólya-Redfield implica el “indicador de ciclo” o “índice de ciclo” de un grupo que actúa sobre un conjunto. Supongamos que tenemos un grupo\(G\) actuando sobre un conjunto finito\(S\). Ya que cada elemento grupal nos\(σ\) da una permutación\(\overline{σ}\) de\(S\), como tal tiene una descomposición en ciclos disjuntos como una permutación de\(S\). Supongamos que\(σ\) tiene\(c_1\) ciclos de tamaño\(1\),\(c_2\) ciclos de tamaño\(2, ..., c_n\) ciclos de tamaño\(n\). Entonces el ciclo monomial de\(σ\) es
\(z(σ) = z_1^{c^1} z_2^{c^2} · · · z_n^{c^n}\).
El indicador de ciclo o índice de ciclo de\(G\) actuación\(S\) es
\(Z(G, S) = \dfrac{1}{|G|} \sum_{σ:σ∈G} z(σ)\).
- ¿Cuál es el índice de ciclo para el grupo\(D_6\) que actúa sobre los vértices de un hexágono?
- ¿Cuál es el índice de ciclo para el grupo de rotaciones del cubo que actúa sobre las caras del cubo?
Ejercicio\(321\)
¿Cómo se puede calcular el Enumerador de Órbitas de\(G\) actuar sobre colorantes de\(S\) por un conjunto finito\(T\) de colores a partir del índice de ciclo de\(G\) actuar sobre ellos\(S\)? (Uso\(t\), pensado como una variable, como la imagen de un elemento\(t\) de\(T\).) ¡Estado y prueba el teorema relevante! Este es el famoso teorema de enumeración de Pólya y Redfield.
\(\rightarrow\) Exercise \(322\)
Supongamos que hacemos un collar\(12\) encordando trozos de tubos de plástico de colores brillantes en una cuerda y sujetando los extremos de la cuerda juntos. Contamos con amplios suministros de tubos azules, verdes, rojos y amarillos disponibles. Dar una función generadora en la que el coeficiente de\(B^iG^jR^kY^h\) es el número de collares que podemos hacer con\(i\) azules,\(j\) verdes,\(k\) rojos y\(h\) amarillos. ¿Cuántos términos tendría esta función generadora si la ampliara en términos de poderes de\(B\),\(G\),\(R\), y\(Y\)? ¿Tiene sentido hacer esta expansión? ¿Cuántos de estos collares tienen\(3\) azules,\(3\) verdes,\(2\) rojos y\(4\) amarillos?
Ejercicio\(323\)
¿Qué debemos sustituir a las variables que representan colores en el enumerador de órbita de\(G\) actuar sobre el conjunto de colorantes de\(S\) por un conjunto\(T\) de colores para calcular el número total de órbitas de\(G\) actuar sobre el conjunto de colorantes? ¿Qué debemos sustituir en las variables en el índice de ciclo de un grupo\(G\) que actúa sobre un conjunto\(S\) para calcular el número total de órbitas de\(G\) actuar sobre los colorantes de\(S\) por un conjunto\(T\)? Encuentra la cantidad de formas de colorear las caras de un cubo con cuatro colores.
\(\rightarrow\) Exercise \(324\)
Tenemos palos rojos, verdes y azules todos de la misma longitud, con una docena de palos de cada color. Vamos a hacer el esqueleto de un cubo tomando ocho terrones idénticos de arcilla modelada y empujando tres palos dentro de cada bulto para que los grumos se conviertan en los vértices del cubo. (Claramente, ¡no vamos a necesitar todos los palos!) ¿De cuántas maneras diferentes podríamos hacer nuestro cubo? ¿Cuántos cubos tienen cuatro bordes de cada color? ¿Cuántos tienen dos bordes rojos, cuatro verdes y seis azules?
\(\rightarrow\) Exercise \(325\)
¿Cuántos cubos podemos hacer en el Problema 324 si los grumos de arcilla para modelar pueden ser de cualquiera de cuatro colores?
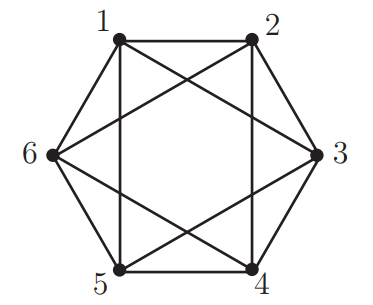
\(\rightarrow\) Exercise \(326\)
En la Figura 6.3.2 vemos una gráfica con seis vértices. Supongamos que tenemos tres tipos diferentes de computadoras que se pueden colocar en los seis vértices de la gráfica para formar una red. ¿De cuántas maneras diferentes se pueden colocar las computadoras? (Dos gráficas no son diferentes si podemos volver a dibujar una de las gráficas para que sea idéntica a la otra). Esto equivale a permutar los vértices de alguna manera para que cuando aplicamos la permutación a los extremos de los bordes para obtener un nuevo conjunto de aristas, el nuevo conjunto de aristas sea igual al anterior. Tal permutación se llama automorfismo de la gráfica. Entonces dos colocaciones de computadora son las mismas si hay un automorfismo de la gráfica que lleva una a la otra. (Pista).
\(\rightarrow\) Exercise \(327\)
Dos gráficas simples sobre el conjunto\([n] = \{1, 2, . . . , n\}\) con conjuntos de bordes\(E\) y\(E'\) (que consideramos como conjuntos de conjuntos de dos elementos para este problema) se dice que son isomórficas si hay una permutación\(σ\) de la\([n]\) cual, en su acción de conjuntos de dos elementos, lleva\(E\) a \(E'\). Decimos que dos gráficas son diferentes si no son isomórficas. Así, el número de diferentes gráficas es el número de órbitas del conjunto de todos los conjuntos de subconjuntos de dos elementos de\([n]\) bajo la acción del grupo\(S_n\). Podemos representar un borde establecido por su función característica (como en el problema 33). Es decir, definimos
\(χ_E(\{u, v\})=\left\{ \begin{array}{ll} 1 \text{ if } \{u, v\} ∈ E\\ 0 \text{ otherwise.} \end{array} \right. \)
Así podemos pensar en el conjunto de gráficas como un conjunto de colorantes con colores\(0\) y en el conjunto\(1\) de todos los subconjuntos de dos elementos de\([n]\). El número de diferentes gráficas con conjunto de vértices\([n]\) es así el número de órbitas de este conjunto de colorantes bajo la acción del grupo simétrico\(S_n\) sobre el conjunto de subconjuntos de dos elementos de\([n]\). Usa esto para encontrar el número de diferentes gráficas en cinco vértices. (Pista).
Notas
1. Hay un tema sutil fascinante de lo que hace que dos moléculas sean diferentes. Por ejemplo, supongamos que tenemos una molécula en forma de cubo, con un átomo en cada vértice. Si cambiamos las caras superior e inferior del cubo, cada átomo sigue estando conectado exactamente a los mismos átomos que antes. Sin embargo, no podemos lograr esta permutación de los vértices por un miembro del grupo de rotación del cubo. Bien podría ser que las dos versiones de la molécula interactúen con otras moléculas de diferentes maneras, en cuyo caso las consideraríamos químicamente diferentes. Por otro lado, si las dos versiones interactúan con otras moléculas de la misma manera, no tendríamos razón para considerarlas químicamente diferentes. Este tipo de simetría es un ejemplo de lo que se llama quiralidad en química.


