13.4: Modelado del Movimiento Espacial
- Page ID
- 115888
Ahora discutiremos cómo escribir un modelo matemático basado en PDE para un proceso dinámico que implica el movimiento espacial de algunas cosas. Hay muchos enfoques para escribir PDEs, pero aquí en este libro de texto, usaremos solo una “plantilla”, llamada la ecuación de transporte. Aquí está la ecuación:
\[\dfrac{\partial{c}}{\partial{t}} = -{∇}·{J} + s \label{13.14} \]
Aquí,\(c\) se define el estado del sistema como una función espacio-temporal que representa la concentración de las cosas que se mueven en el espacio. \({J}\)es un campo vectorial llamado el flux de\(c\). La magnitud del vector\(J\) en una ubicación particular representa el número de partículas que se mueven a través de una sección transversal del espacio por área por unidad de tiempo en esa ubicación. Tenga en cuenta que esto es exactamente lo mismo que el campo vectorial\(v\) que discutimos cuando tratamos de entender el significado de la divergencia. Por lo tanto, el primer término de la Ecuación\ ref {13.14} viene directamente de la Ecuación (13.2.11). El segundo término,\(s\), a menudo se denomina término fuente/sumidero, que es un campo escalar que representa cualquier aumento o disminución de que se\(c\) produzca localmente. Esto es a menudo el resultado de influx o outflux de partículas desde/hacia el exterior del sistema. Si el sistema está cerrado y se conserva la cantidad total de las cosas, no se necesita el término fuente/sumidero, y la ecuación de transporte se vuelve idéntica a la ecuación (13.2.11).
Hay otra forma de escribir una ecuación de transporte. Mientras que la Ecuación\ ref {13.14} describe explícitamente la cantidad de movimiento de las partículas por área por unidad de tiempo en forma de flux\(J\), otra manera conveniente de describir el movimiento es especificar la velocidad de las partículas, y luego asumir que todas las partículas se mueven a esa velocidad. Específicamente:
\[\dfrac{\partial{c}}{\partial{t}} = −∇·(cw) + s \label{13.15} \]
Aquí,\(w\) está el campo vectorial que representa la velocidad de las partículas en cada ubicación. Ya que todas las partículas se mueven a esta velocidad, el flux viene dado por\(J = cw.\) Qué formulación debes usar, Ecuación\ ref {13.14} o Ecuación\ ref {13.15}, depende de la naturaleza del sistema que vayas a modelar.
Como puedes ver arriba, la ecuación del transporte es muy sencilla. Pero es bastante útil como punto de partida cuando se quiere describir diversos tipos de fenómenos espaciales. Un ejemplo es derivar una ecuación de difusión. ¿Cómo se puede escribir un modelo de dinámica de difusión basado en PDE mediante el cual la distribución espacial de las cosas tiende a suavizarse con el tiempo (Figura\(\PageIndex{1}\))?
Para desarrollar un modelo de difusión utilizando la ecuación de transporte, necesitamos pensar en la dirección del movimiento en este proceso. En difusión, las partículas tienden a moverse aleatoriamente a escalas microscópicas, pero macroscópicamente, tienden a “flotar” de alto a bajo, bajando las jorobas mientras llenan las inmersiones (Figura\(\PageIndex{1}\), izquierda), resultando finalmente en una superficie completamente nivelada. Por lo tanto, una elección natural de la dirección del movimiento de las partículas es la opuesta al gradiente de la distribución de las partículas (\(−α∇c\), donde\(α\) es una constante positiva).
La siguiente pregunta que quizás quieras hacer es: ¿Qué fórmula debes usar, Ecuación\ ref {13.14} o Ecuación\ ref {13.15}? Para tomar una decisión, debes pensar si\(−α∇c\) solo da la velocidad de movimiento o también determina la magnitud real del flux. Si el primero es el caso, todas las partículas en la misma ubicación se moverán hacia esa dirección, por lo que el flux real debe ser dado por\(−c(α∇c)\). Pero esto significa que la velocidad de difusión será más rápida si todo el sistema se “eleva” al agregar 10 a\(c\) todas partes. En otras palabras, ¡la velocidad de difusión dependerá de la elevación del terreno! Esto no suena del todo bien, porque la difusión es un proceso de alisado de la superficie, que solo debe depender de la forma de la superficie y no debe verse afectado por qué tan alta o baja se eleva la superficie general. Por lo tanto, en este caso, la Ecuación\ ref {13.14} es la elección correcta; debemos considerar\(−α∇c\) el flux real causado por la difusión. A este supuesto se le llama la primera ley de difusión de Fick, ya que fue propuesta por Adolf Fick en el siglo XIX.
Al conectarnos\(J = −α∇c \) a la ecuación\ ref {13.14}, obtenemos
\[\begin{align} \dfrac{\partial{c}}{\partial{t}} &= −∇·(−α∇c) + s \\[4pt] &= ∇·(α∇c) + s. \label{(13.16)} \end{align} \]
Si\(α\) es una constante homogénea que no depende de ubicaciones espaciales, entonces podemos sacarla de los paréntesis:
\[\dfrac{\partial{c}}{\partial{t}}=α∇^{2}c + s \label{(13.17)} \]
¡Ahora vemos salir al Laplaciano! Esto se llama la ecuación de difusión, una de las PDE más fundamentales que se ha aplicado a muchas dinámicas espacio-temporales en física, biología, ecología, ingeniería, ciencias sociales, ciencias del marketing y muchas otras disciplinas. Esta ecuación también se llama la ecuación de calor o la segunda ley de difusión de Fick. \(α\)se llama la constante de difusión, que determina qué tan rápido se produce la difusión.
Todavía podríamos considerar un modelo de suavizado alternativo en el que el flux viene dado por\(−c(α∇c)\), que hace la siguiente ecuación del modelo:
\[\dfrac{\partial{c}}{\partial{t}} =α∇·(c∇c) + s \label{(13.18)} \]
Explique qué tipo de comportamiento está modelando esta ecuación. Discutir la diferencia entre este modelo y la ecuación de difusión (Ecuación\ ref {(13.17)}).
Desarrollar un modelo PDE que describa un movimiento circular de partículas alrededor de cierto punto en el espacio.
Desarrollar un modelo PDE que describa la atracción de partículas entre sí.
Podemos desarrollar modelos de campo continuos más complejos combinando movimiento espacial y dinámica local juntos, y también incluyendo más de una variable de estado. Intentemos desarrollar un modelo basado en PDE de interacciones entre dos variables estatales: distribución poblacional (\(p\)para “personas”) y actividad económica (\(m\)para “dinero”). Su dinámica local (no espacial) se asume de la siguiente manera:
1. La población nunca aumentará o disminuirá dentro de la escala de tiempo que se está considerando en este modelo.
2. La economía se activa al tener más gente en una región.
3. La economía disminuye sin personas.
Mientras tanto, su dinámica espacial (movimientos) se asume de la siguiente manera:
4. Tanto la población como la actividad económica se difunden gradualmente.
5. La gente se siente atraída por las regiones donde la economía es más activa.
Nuestro trabajo es traducir estos supuestos en ecuaciones matemáticas rellenando los recuadros a continuación.
\(\dfrac{\partial{p}}{\partial{t}} = \Box \)
\(\dfrac{\partial{m}}{\partial{t}} = \Box \)
Primero, ¡pruébalo tú mismo! Después pasa a lo siguiente.
¿Pudiste desarrollar tu propio modelo? Repasemos todos los supuestos para ver cómo podemos escribir cada uno de ellos en forma matemática.
El supuesto 1 dice que no hay cambio en la población por defecto. Entonces, esto puede escribirse simplemente como
\[\dfrac{\partial{m}}{\partial{t}} =\alpha{p}, \label{(13.19)} \]
donde\(α\) es una constante positiva que determina la tasa de producción de la economía per cápita.
La suposición 3 dice que la economía debería decaer naturalmente si no hay influencia de la gente. El modelo más simple de tal decaimiento sería el de decaimiento exponencial, que puede representarse incluyendo un término lineal de\(m\) con un coeficiente negativo en la ecuación para\(m\), de manera que:
\[\dfrac{\partial{m}}{\partial{t}} =\alpha{p} -\beta {m}. \label{(13.21)} \]
Nuevamente,\(β\) es una constante positiva que determina la tasa de decaimiento de la economía. Esta ecuación muestra correctamente el decaimiento exponencial si\(p = 0\), lo que concuerda con la suposición. Hasta el momento, todos los supuestos implementados son sobre dinámicas locales, no espaciales. Por lo tanto, no vimos ninguna derivada espacial.
Ahora, la Asunción 4 dice que debemos dejar que la gente y el dinero se difundan sobre el espacio Se trata del movimiento espacial. Se puede modelar usando la ecuación de difusión que discutimos anteriormente (Ecuación\ ref {(13.17)}). No hay necesidad de agregar términos de fuente/sumidero, así que solo agregamos términos laplacianos a ambas ecuaciones:
\[\dfrac{\partial{p}}{\partial{t}} = D_{p}∇^{2}p \label{(13.22)} \]
\[\dfrac{\partial{m}}{\partial{t}} =D_{m}∇^{2}m +\alpha{p} -\beta{m} \label{(13.23)} \]
Aquí,\(D_p\) y\(D_m\) están las constantes positivas de difusión de personas y dinero, respectivamente.
Por último, la Asunción 5 dice que la gente puede sentir el “olor” del dinero y moverse hacia áreas donde hay más dinero. Aquí es donde podemos usar la ecuación de transporte. En este caso, podemos usar la Ecuación\ ref {13.15}, porque todas las personas en un lugar determinado estarían sintiendo el mismo “olor” y así se estarían moviendo hacia la misma dirección en promedio. Podemos representar este movimiento en el siguiente término de transporte
\[−∇·(p γ∇m), \label{(13.24)} \]
donde\(m\) se utiliza el gradiente de para obtener la velocidad promedio del movimiento popular (con otra constante positiva\(γ\)). Añadiendo este término a la ecuación para\(p\) representael movimiento de las personas hacia el dinero.
Entonces, las ecuaciones modelo completadas se ven así:
\[\dfrac{\partial{p}}{\partial{t}} =D_{p} \nabla^{2}p -\gamma \nabla \cdot(p\nabla{m}) \label{(13.25)} \]
\[\dfrac{\partial{m}}{\partial{t}} =D_{m} \nabla^{2}m +\alpha{m} -\beta{m} \label{(13.26)} \]
¿Cómo se compara este modelo con el tuyo?
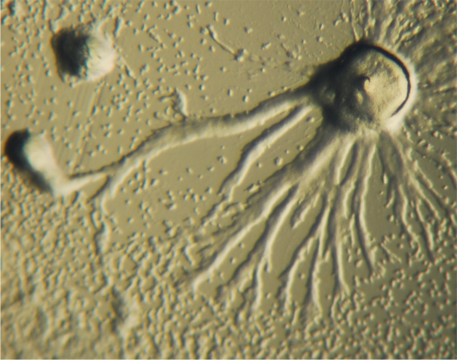
Curiosamente, un modelo matemático que era esencialmente idéntico a nuestras ecuaciones anteriores fue propuesto hace casi medio siglo por dos físicos/matemáticos aplicados, Evelyn Keller y Lee Segel, para describir un fenómeno biológico completamente diferente [48, 49]. El modelo de Keller-Segel fue desarrollado para describir la quimiotaxis —movimiento de organismos hacia (o alejándose de) ciertas señales químicas— de una especie de moho de limo celular Dictyostelium discoideum. Estas celdas de moho de limo normalmente se comportan como amebas individuales y se alimentan de bacterias, pero cuando el suministro de alimentos se vuelve bajo, primero se esparcen por el espacio y luego se agregan para formar “babosas” para la migración a larga distancia (Figura\(\PageIndex{2}\)). Keller y Segel desarrollaron un modelo matemático de este proceso de agregación, donde la quimiotaxis juega un papel crítico en la autoorganización celular.
Keller y Segel hicieron los siguientes supuestos basados en lo que ya se sabía sobre estos interesantes organismos celulares:
- Las células se distribuyen inicialmente sobre un espacio de manera más o menos homogénea (con algunas fluctuaciones aleatorias).
- Las células muestran quimiotaxis hacia una señal química llamada AMPc (monofosfato de adenosina cíclico).
- Las células producen moléculas de AMPc.
- Tanto las células como las moléculas de cAMP se difunden sobre el espacio
- Las células no mueren ni se dividen.
¿Se dio cuenta de la similitud entre estos supuestos y los que utilizamos para el modelo población-economía? En efecto, son idénticos, sireemplazas “células” por “personas” y “cAMP” con “dinero”. ¡Podríamos usar la palabra “moneytaxis” para la migración de personas hacia áreas económicamente activas!
Las ecuaciones reales de Keller-Segel se ven así:
\[\dfrac{\partial{a}}{\partial{t}} =\mu\nabla^{2}\alpha -\chi \nabla \cdot (a\nabla{c}) \label{(13.27)} \]
\[\dfrac{\partial{c}}{\partial{t}} D \nabla^{2}c +fa-kc \label{(13.28)} \]
De hecho, estas ecuaciones son simplificadas dadas en [49], ya que las ecuaciones originales fueron bastante complicadas con más detalles biológicos. \(a\)y\(c\) son las variables de estado para la densidad celular y la concentración de AMPc, respectivamente. \(µ\)es el parámetro para la movilidad celular,\(χ\) es el parámetro para la quimiotaxis celular,\(D\) es la constante de difusión de AMPc,\(f\) es la tasa de secreción de AMPc por las células y\(k\) es la tasa de decaimiento de AMPc. Compara estas ecuaciones con las ecuaciones. \ ref {(13.25)} y\ ref {(13.26)}. ¡Son lo mismo! Es intrigante ver que fenómenos completamente diferentes a escalas espacio-temporales muy distantes podrían modelarse en una formulación matemática idéntica.
Se sabe que, para ciertos ajustes de parámetros (que se discutirán en el siguiente capítulo), este modelo muestra la formación espontánea de patrones a partir de condiciones iniciales casi homogéneas. Un resultado de simulación de muestra se muestra en la Fig. 13.4.3, donde vemos manchas de clústeres celulares agregados formando espontáneamente. Aprenderás a realizar simulaciones de modelos de campo continuos en la siguiente sección.
En la Fig. 13.4.3, también podemos observar que existe una distancia característica entre puntos cercanos, la cual está determinada por parámetros del modelo (especialmente constantes de difusión). La misma observación se aplica a la formación de ciudades y pueblos a escalas geográficas. Cuando veas un mapa, probablemente notarás que existe una distancia típica entre las principales ciudades, que probablemente estuvo determinada por la movilidad humana hace siglos, entre otros factores.
Considera introducir al modelo de Keller-Segel una nueva variable b que represente la concentración de un químico de desechos tóxicos. Haga las siguientes suposiciones:
- El AMPc se convierte gradualmente en el químico de desecho (además de la descomposición natural).
- El residuo químico se difunde sobre el espacio.
- El residuo químico nunca se descomponga de forma natural.
- Las células tienden a evitar regiones con altas concentraciones del residuo químico.
- Revisar las ecuaciones de Keller-Segel para desarrollar su nuevo modelo.
Desarrollar un modelo basado en PDE que describa la dinámica de un ecosistema depredador-presa con los siguientes supuestos:
- La población de presas crece siguiendo el modelo de crecimiento logístico.
- La población depredadora tiende a decaer naturalmente sin presas.
- La depredación (es decir, el encuentro de presas y poblaciones de depredadores) aumenta la población depredadora mientras disminuye la población de presas.
- La población depredadora tiende a desplazarse hacia áreas con alta densidad de presas.
- La población de presas tiende a alejarse de áreas con alta densidad de depredadores.
- Ambas poblaciones se difunden sobre el espacio.