9.7: La ecuación de Laplace

La ecuación de difusión en dos dimensiones espaciales es\[u_t=D(u_{xx}+u_{yy}).\nonumber\]

La solución de estado estacionario, abordada asintóticamente en el tiempo, tiene\(u_t = 0\) tal que la solución de estado estacionario\(u = u(x, y)\) satisface la ecuación bidimensional de Laplace \[\label{eq:1}u_{xx}+u_{yy}=0.\]

Consideraremos el problema matemático de resolver la ecuación bidimensional de Laplace dentro de un límite rectangular o circular. El valor de se\(u(x, y)\) especificará en los límites, definiendo este problema como de tipo Dirichlet.

Problema de Dirichlet para un rectángulo

Figura\(\PageIndex{1}\): Problema de Dirichlet para la ecuación de Laplace en un rectángulo.

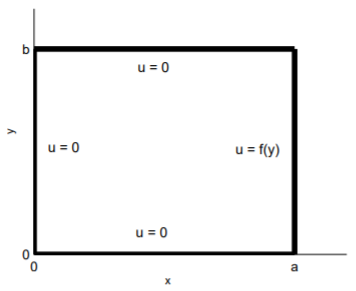
Consideramos la ecuación de Laplace\(\eqref{eq:1}\) para el interior de un rectángulo\(0 < x < a\),\(0 < y < b\), (ver Fig. \(\PageIndex{1}\)), con condiciones de límite\[\begin{array}{lllll}u(x,0)=0, && u(x,b)=0, && 0<x<a; \\ u(0,y)=0, && u(a,y)=f(y),&& 0\leq y\leq b.\end{array}\nonumber\]

Las condiciones de contorno más generales se pueden resolver mediante superposición lineal de soluciones.

Tomamos nuestro ansatz habitual\[u(x,y)=X(x)Y(y),\nonumber\] y encontramos después de la sustitución en\(\eqref{eq:1}\),\[\frac{X''}{X}=-\frac{Y''}{Y}=\lambda,\nonumber\] con\(\lambda\) la constante de separación. Obtenemos así las dos ecuaciones diferenciales ordinarias\[X''-\lambda X=0,\quad Y''+\lambda Y=0.\nonumber\]

Las condiciones de contorno homogéneas son\(X(0) = 0,\: Y(0) = 0\) y\(Y(b) = 0\). Ya hemos resuelto la ecuación para\(Y(y)\) en §9.5, y la solución arroja los valores propios\[\lambda_n=\left(\frac{n\pi}{b}\right)^2,\quad n=1,2,3,\ldots ,\nonumber\] con las correspondientes funciones propias\[Y_n(y)=\sin\frac{n\pi y}{b}.\nonumber\]

La\(X\) ecuación restante y la condición de límite homogéneo es, por lo tanto,\[X''-\frac{n^2\pi^2}{b^2}X=0,\quad X(0)=0,\nonumber\] y la solución es la función sinusoidal hiperbólica\[X_n(x)=\sinh\frac{n\pi x}{b},\nonumber\] por una constante. Escribir\(u_n = X_nY_n\), multiplicar por una constante y sumar\(n\), arroja la solución general\[u(x,y)=\sum\limits_{n=0}^\infty c_n\sinh\frac{n\pi x}{b}\sinh\frac{n\pi y}{b}.\nonumber\]

La condición de límite no homogénea restante da como\(u(a, y) = f(y)\) resultado la\[f(y)=\sum\limits_{n=0}^\infty c_n\sinh\frac{n\pi a}{b}\sin\frac{n\pi y}{b},\nonumber\] cual reconocemos como una serie sinusoidal de Fourier para una función impar con período\(2b\) y coeficiente\(c_n \sinh (n\pi a/b)\). La solución para el coeficiente viene dada por\[c_n=\frac{2}{b\sinh\frac{n\pi a}{b}}\int_0^b f(y)\sin\frac{n\pi y}{b}dy.\nonumber\]

Problema de Dirichlet para un círculo

La ecuación de Laplace se escribe comúnmente simbólicamente como \[\label{eq:2}\nabla ^2u=0,\]donde\(\nabla^2\) se llama el Laplaciano, a veces denotado como\(\Delta\). El Laplaciano se puede escribir en varios sistemas de coordenadas, y la elección de los sistemas de coordenadas suele depender de la geometría de los límites. En efecto, ¡se sabe que la ecuación de Laplace es separable en\(13\) diferentes sistemas de coordenadas! Hemos resuelto la ecuación de Laplace en dos dimensiones, con condiciones de contorno especificadas en un rectángulo, usando\[\nabla ^2=\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}.\nonumber\]

Aquí consideramos las condiciones de límite especificadas en un círculo, y escribimos el laplaciano en coordenadas polares cambiando variables a partir de coordenadas cartesianas. Las coordenadas polares se definen por la transformación\((r,\theta )\to (x, y)\):

\[\label{eq:3}x=r\cos\theta,\quad y=r\sin\theta ;\]y la regla de la cadena da para las derivadas parciales \[\label{eq:4}\frac{\partial u}{\partial r}=\frac{\partial u}{\partial x}\frac{\partial x}{\partial r}+\frac{\partial u}{\partial y}\frac{\partial y}{\partial r},\quad \frac{\partial u}{\partial\theta}=\frac{\partial u}{\partial x}\frac{\partial x}{\partial\theta}+\frac{\partial u}{\partial y}\frac{\partial y}{\partial\theta}.\]

Después de tomar las derivadas parciales de\(x\) y\(y\) usar\(\eqref{eq:3}\), podemos escribir la transformación\(\eqref{eq:4}\) en forma de matriz como \[\label{eq:5}\left(\begin{array}{c}\partial u/\partial r \\ \partial u/\partial\theta\end{array}\right)=\left(\begin{array}{rr}\cos\theta &\sin\theta \\ -r\sin\theta & r\cos\theta\end{array}\right)\left(\begin{array}{c}\partial u/\partial x \\ \partial u/\partial y\end{array}\right).\]

La inversión de se\(\eqref{eq:5}\) puede determinar a partir del siguiente resultado, comúnmente probado en una clase de álgebra lineal. Si\[A=\left(\begin{array}{cc}a&b \\ c&d\end{array}\right),\quad\det A\neq 0,\nonumber\] entonces\[A^{-1}=\frac{1}{\det A}\left(\begin{array}{cc}d&-b \\ -c&a\end{array}\right).\nonumber\]

Por lo tanto, dado que el determinante de la\(2\times 2\) matriz en\(\eqref{eq:5}\) es\(r\), tenemos \[\label{eq:6}\left(\begin{array}{c}\partial u/\partial x \\ \partial u/\partial y\end{array}\right)=\left(\begin{array}{rr}\cos\theta &-\sin\theta /r \\ \sin\theta &\cos\theta /r\end{array}\right)\left(\begin{array}{c}\partial u/\partial r \\ \partial u/\partial\theta\end{array}\right).\]

Reescribiendo\(\eqref{eq:6}\) en forma de operador, tenemos \[\label{eq:7}\frac{\partial}{\partial x}=\cos\theta\frac{\partial}{\partial r}-\frac{\sin\theta}{r}\frac{\partial}{\partial\theta},\quad\frac{\partial}{\partial y}=\sin\theta\frac{\partial}{\partial r}+\frac{\cos\theta}{r}\frac{\partial}{\partial\theta}.\]

Para encontrar al Laplaciano en coordenadas polares con álgebra mínima, combinamos\(\eqref{eq:7}\) utilizando variables complejas de \[\label{eq:8}\frac{\partial}{\partial x}+i\frac{\partial}{\partial y}=e^{i\theta}\left(\frac{\partial}{\partial r}+\frac{i}{r}\frac{\partial}{\partial\theta}\right),\]manera que el Laplaciano se pueda encontrar multiplicando ambos lados de\(\eqref{eq:8}\) por su complejo conjugado, cuidando con el cómputo de las derivadas de la derecha- lado:

\[\begin{aligned}\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}&=e^{i\theta}\left(\frac{\partial}{\partial r}+\frac{i}{r}\frac{\partial}{\partial\theta}\right)e^{-i\theta}\left(\frac{\partial}{\partial r}-\frac{1}{r}\frac{\partial}{\partial\theta}\right) \\ &=\frac{\partial ^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^2}\frac{\partial ^2}{\partial\theta ^2}.\end{aligned}\]

Por lo tanto, hemos determinado que el laplaciano en coordenadas polares viene dado por \[\label{eq:9}\nabla^2=\frac{\partial ^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^2}\frac{\partial ^2}{\partial\theta^2},\]lo que a veces se escribe como\[\nabla^2 =\frac{1}{r}\frac{\partial}{\partial r}\left(r\frac{\partial}{\partial r}\right)+\frac{1}{r^2}\frac{\partial ^2}{\partial\theta ^2}.\nonumber\]

Consideramos ahora la solución de la ecuación de Laplace en un círculo con radio\(r < a\) sujeto a la condición límite \[\label{eq:10}u(a,\theta )=f(\theta),\quad 0\leq\theta\leq 2\pi.\]

Una condición de límite adicional debido al uso de coordenadas polares es que\(u(r, \theta )\) es periódica en\(\theta\) con periodo\(2\pi\). Además, también asumiremos que\(u(r, \theta )\) es finito dentro del círculo.

El método de separación de variables toma como nuestro ansatz\[u(r,\theta )=R(r)\Theta (\theta ),\nonumber\] y la sustitución en la ecuación de Laplace\(\eqref{eq:2}\) usando\(\eqref{eq:9}\) rendimientos\[R''\Theta +\frac{1}{r}R'\Theta +\frac{1}{r^2}R\Theta ''=0,\nonumber\] o\[r^2\frac{R''}{R}+r\frac{R'}{R}=-\frac{\Theta ''}{\Theta }=\lambda,\nonumber\] donde\(\lambda\) está la constante de separación. Obtenemos así las dos ecuaciones diferenciales ordinarias\[r^2R''+rR'-\lambda R=0,\quad \Theta ''+\lambda\Theta =0.\nonumber\]

La\(\Theta\) ecuación se resuelve asumiendo condiciones de límite periódicas con periodo\(2\pi\). Si\(\lambda < 0\), entonces no existe una solución periódica. Si\(\lambda = 0\), entonces\(\Theta\) puede ser constante. Si\(\lambda = \mu^2 > 0\), entonces\[\Theta (\theta )=A\cos\mu\theta +B\sin\mu\theta ,\nonumber\] y el requisito que\(\Theta\) es periódico con periodo\(2\pi\) obliga\(\mu\) a ser un entero. Por lo tanto,\[\lambda_n=n^2,\quad n=0,1,2,\ldots ,\nonumber\] con las correspondientes funciones propias\[\Theta_n(\theta )=A_n\cos n\theta +B_n\sin n\theta.\nonumber\]

La\(R\) ecuación para cada valor propio se convierte\(\lambda_n\) entonces en \[\label{eq:11}r^2R''+rR'-n^2R=0,\]que es una ecuación de Euler. Con el ansatz\(R = r^s\),\(\eqref{eq:11}\) reduce a la ecuación algebraica\(s(s − 1) + s − n^2 = 0\), o\(s^2 = n^2\). Por lo tanto\(s = ±n\),, y hay dos soluciones reales cuando\(n > 0\) y degeneran soluciones cuando\(n = 0\). Cuando\(n > 0\), la solución para\(R(r)\) es\[R_n(r)=Ar^n+Br^{-n}.\nonumber\]

El requisito que\(u(r,\theta )\) es finito en las fuerzas del círculo\(B = 0\) ya que\(r^{−n}\) se vuelve sin límites como\(r\to 0\). Cuando\(n = 0\), la solución para\(R(r)\) es\[R_n(r)=A+B\ln r,\nonumber\] y nuevamente finita\(u\) en las fuerzas del círculo\(B = 0\). Por lo tanto, la solución para\(n = 0,\: 1,\: 2,\ldots\) es\(R_n = r^n\). Así, la solución general para\(u(r,\theta )\) puede escribirse como \[\label{eq:12} u(r,\theta )=\frac{A_0}{2}+\sum\limits_{n=1}^\infty r^n (A_n\cos n\theta +B_n\sin n\theta ),\]donde hemos separado la\(n = 0\) solución para escribir nuestra solución en una forma similar a la serie estándar de Fourier dada por (9.3.1). La condición de contorno restante\(\eqref{eq:10}\) especifica los valores de u en el círculo de radio a, y la imposición de esta condición de límite da como resultado \[\label{eq:13} f(\theta )=\frac{A_0}{2}+\sum\limits_{n=1}^\infty a^n (A_n\cos n\theta +B_n\sin n\theta ).\]

\(\eqref{eq:13}\)La ecuación es una serie de Fourier para la función periódica\(f(\theta )\) con periodo\(2\pi\), es decir,\(L = \pi\) en (9.3.1). Los coeficientes de Fourier\(a^nA_n\) y por lo tanto\(a^nB_n\) están dados por (9.3.5) y (9.3.6) para estar \[\begin{align} a^nA_n&=\frac{1}{\pi}\int_0^{2\pi} f(\phi )\cos n\phi d\phi, \quad n=0,1,2,\ldots ; \nonumber \\ a^nB_n&=\frac{1}{\pi}\int_0^{2\pi}f(\phi )\sin n\phi d\phi ,\quad n=1,2,3,\ldots ,\label{eq:14}\end{align}\]donde hemos utilizado\(\phi\) para la variable ficticio de integración.

Un hecho notable es que la solución de series infinitas para se\(u(r, \theta )\) puede sumar explícitamente. Sustituyendo\(\eqref{eq:14}\) en\(\eqref{eq:12}\), obtenemos\[\begin{aligned}u(r,\theta )&=\frac{1}{2\pi}\int_0^{2\pi}d\phi f(\phi )\left[ 1+2\sum\limits_{n=1}^\infty \left(\frac{r}{a}\right)^n (\cos n\theta\cos n\phi +\sin n\theta\sin n\phi )\right] \\ &=\frac{1}{2\pi}\int_0^{2\pi} d\phi f(\phi)\left[1+2\sum_{n=1}^\infty \left(\frac{r}{a}\right)^n\cos n(\theta -\phi)\right].\end{aligned}\]

Podemos sumar las series infinitas escribiendo\(2 cos n(\theta − \phi ) = e^{in(\theta−\phi)} + e^{−in(\theta −\phi)}\), y usando la suma de las series geométricas\(\sum_{n=1}^\infty z^n = z/(1 − z)\) para obtener\[\begin{aligned} 1+2\sum\limits_{n=1}^\infty \left(\frac{r}{a}\right)^n\cos n(\theta -\phi)&=1+\sum\limits_{n=1}^\infty \left(\frac{re^{i(\theta -\phi)}}{a}\right)^n +\sum\limits_{n=1}^\infty \left(\frac{re^{-i(\theta -\phi )}}{a}\right)^n \\ &=1+\left(\frac{re^{i(\theta -\phi)}}{a-re^{i(\theta -\phi )}}+c.c.\right) \\ &=\frac{a^2-r^2}{a^2-2ar\cos (\theta -\phi )+r^2}.\end{aligned}\]

Por lo tanto,\[u(r,\theta )=\frac{a^2-r^2}{2\pi}\int_0^{2\pi}\frac{f(\phi )}{a^2-2ar\cos (\theta -\phi )+r^2}d\phi,\nonumber\] un resultado integral para\(u(r, \theta )\) conocido como fórmula de Poisson. Como ejemplo trivial, considera la solución para\(u(r, \theta )\) si\(f(\theta ) = F\), una constante. Claramente,\(u(r, \theta ) = F\) satisface tanto la ecuación de Laplace como las condiciones límite por lo que debe ser la solución. Se puede verificar que efectivamente\(u(r, \theta ) = F\) es la solución demostrando que\[\int_0^{2\pi}\frac{d\phi}{a^2-2ar\cos (\theta -\phi )+r^2}=\frac{2\pi }{a^2-r^2}.\nonumber\]