7.3: Los puntos singulares y el método de Frobenius

Ejemplos

Si bien el comportamiento de las ODE en puntos singulares es más complicado, ciertos puntos singulares no son especialmente difíciles de resolver. Veamos algunos ejemplos antes de dar un método general. Podemos tener suerte y obtener una solución de series de potencia utilizando el método de la sección anterior, pero en general puede que tengamos que probar otras cosas.

Ejemplo\(\PageIndex{1}\)

Veamos primero una simple ecuación de primer orden

\[2 x y' - y = 0 . \label{ex1eq1} \]

Tenga en cuenta que\(x=0\) es un punto singular. Si solo intentamos enchufar

\[y = \sum_{k=0}^\infty a_k x^k ,\label{ex1eq2} \]

obtenemos

\[\begin{align}\begin{aligned} 0 = 2 xy'-y &=2x \, \left( \sum_{k=1}^\infty k a_k x^{k-1} \right)-\left( \sum_{k=0}^\infty a_k x^k \right) \\ &=a_0 +\sum_{k=1}^\infty (2 k a_k - a_k) \, x^{k} . \end{aligned}\end{align} \label{ex1eq3} \]

Primero,\(a_0 = 0\). A continuación, la única manera de resolver\(0 = 2 k a_k - a_k = (2k-1) \, a_k\) para\(k = 1,2,3,\dots\) es\(a_k = 0\) para todos\(k\). Por lo tanto solo conseguimos la solución trivial\(y=0\). Necesitamos una solución distinta de cero para obtener la solución general.

Intentemos\(y=x^r\) por algún número real\(r\). En consecuencia, nuestra solución, si podemos encontrar una, puede que solo tenga sentido para positivo\(x\). Entonces\(y' = r x^{r-1}\). Entonces

\[ 0 = 2 x y' - y = 2 x r x^{r-1} - x^r= (2r-1) x^r . \nonumber \]

Por lo tanto\(r= \dfrac{1}{2}\), o en otras palabras\(y = x^{1/2}\). Multiplicando por una constante, la solución general para positivo\(x\) es

\[y = C x^{1/2} . \nonumber \]

Si\(C \not= 0\) entonces la derivada de la solución “estalla” en\(x=0\) (el punto singular). Solo hay una solución que es diferenciable en\(x=0\) y esa es la solución trivial\(y=0\).

No todo problema con un punto singular tiene una solución de la forma\(y=x^r\), por supuesto. Pero quizá podamos combinar los métodos. Lo que haremos es probar una solución de la forma

\[y = x^r f(x) \nonumber \]

donde\(f(x)\) es una función analítica.

Ejemplo\(\PageIndex{2}\)

Supongamos que tenemos la ecuación

\[4 x^2 y'' - 4 x^2 y' + (1-2x)y = 0, \label{ex2eq1} \]

y nuevamente señalar que\(x=0\) es un punto singular. Vamos a probar

\[ y = x^r \sum_{k=0}^\infty a_k x^k = \sum_{k=0}^\infty a_k x^{k+r} , \label{ex2eq2} \]

donde\(r\) es un número real, no necesariamente un número entero. Nuevamente si tal solución existe, sólo puede existir para positivo\(x\). Primero encontremos los derivados

\[ \begin{align} y' &= \sum_{k=0}^\infty (k+r)\, a_k x^{k+r-1} ,\nonumber \\ y'' &= \sum_{k=0}^\infty (k+r)\,(k+r-1)\, a_k x^{k+r-2} . \label{ex2eq3} \end{align} \]

Conectando Ecuaciones\ ref {ex2eq2} -\ ref {ex2eq3} en nuestra ecuación diferencial original (Ecuación\ ref {ex2eq1}) obtenemos

\[ \begin{align}\begin{aligned} 0 &= 4x^2y''-4x^2y'+(1-2x)y \\ &= 4x^2 \, \left( \sum_{k=0}^\infty (k+r)\,(k+r-1) \, a_k x^{k+r-2} \right)-4x^2 \, \left( \sum_{k=0}^\infty (k+r) \, a_k x^{k+r-1} \right)+(1-2x) \left( \sum_{k=0}^\infty a_k x^{k+r} \right) \\ &=\left( \sum_{k=0}^\infty 4 (k+r)\,(k+r-1) \, a_k x^{k+r} \right)-\left( \sum_{k=0}^\infty 4 (k+r) \, a_k x^{k+r+1} \right)+\left( \sum_{k=0}^\infty a_k x^{k+r} \right)-\left( \sum_{k=0}^\infty 2a_k x^{k+r+1} \right) \\ &=\left( \sum_{k=0}^\infty 4 (k+r)\,(k+r-1) \, a_k x^{k+r} \right)-\left( \sum_{k=1}^\infty 4 (k+r-1) \, a_{k-1} x^{k+r} \right)+\left( \sum_{k=0}^\infty a_k x^{k+r} \right)-\left( \sum_{k=1}^\infty 2a_{k-1} x^{k+r} \right)\\ &=4r(r-1) \, a_0 x^r + a_0 x^r +\sum_{k=1}^\infty \left( 4 (k+r)\,(k+r-1) \, a_k - 4 (k+r-1) \, a_{k-1}+a_k -2a_{k-1} \right) \, x^{k+r}\\ &=\left( 4r(r-1) + 1 \right) \, a_0 x^r +\sum_{k=1}^\infty\left( \left( 4 (k+r)\,(k+r-1) + 1 \right) \, a_k-\left( 4 (k+r-1) + 2 \right) \, a_{k-1} \right) \, x^{k+r} .\end{aligned}\end{align} \nonumber \]

Para tener una solución debemos tener primero\(\left( 4r(r-1) + 1 \right) \, a_0 = 0\). Suponiendo que\(a_0 \not= 0\) obtengamos

\[4r(r-1) + 1 = 0 . \nonumber \]

Esta ecuación se llama la ecuación indicial. Esta ecuación indicial particular tiene una doble raíz en\(r = \dfrac{1}{2}\).

Bien, entonces sabemos lo que\(r\) tiene que ser. Ese conocimiento lo obtuvimos simplemente mirando el coeficiente de\(x^r\). Todos los demás coeficientes de\(x^{k+r}\) también tienen que ser cero así

\[\left( 4 (k+r)\,(k+r-1) + 1 \right) \, a_k- \left( 4 (k+r-1) + 2 \right) \, a_{k-1} = 0 . \nonumber \]

Si enchufamos\(r=\dfrac{1}{2}\) y\(a_k\) resolvemos para obtenemos

\[a_k=\dfrac{4 (k+\dfrac{1}{2}-1) + 2}{4 (k+\dfrac{1}{2})\,(k+\dfrac{1}{2}-1) + 1} \, a_{k-1}=\dfrac{1}{k} \, a_{k-1} . \nonumber \]

Vamos a ponernos\(a_0 = 1\). Entonces

\[a_1 = \dfrac{1}{1} a_0 = 1 , \qquad a_2 = \dfrac{1}{2} a_1 = \dfrac{1}{2} ,\qquad a_3 = \dfrac{1}{3} a_2 = \dfrac{1}{3 \cdot 2} ,\qquad a_4 = \dfrac{1}{4} a_3 = \dfrac{1}{4 \cdot 3 \cdot 2} , \qquad \dots \nonumber \]

Extrapolando, notamos que

\[a_k = \dfrac{1}{k(k-1)(k-2) \cdots 3 \cdot 2} = \dfrac{1}{k!} . \nonumber \]

En otras palabras,

\[y =\sum_{k=0}^\infty a_k x^{k+r}=\sum_{k=0}^\infty \dfrac{1}{k!} x^{k+1/2}=x^{1/2} \sum_{k=0}^\infty \dfrac{1}{k!} x^{k}=x^{1/2}e^x . \nonumber \]

¡Eso fue suerte! En general, no podremos escribir la serie en términos de funciones elementales. Tenemos una solución, llamémosla\(y_1 = x^{1/2} e^x\). Pero, ¿qué pasa con una segunda solución? Si queremos una solución general, necesitamos dos soluciones linealmente independientes. Escoger\(a_0\) para ser una constante diferente sólo nos consigue un múltiplo constante de\(y_1\), y no tenemos otra que\(r\) probar; sólo tenemos una solución a la ecuación indicial. Bueno, hay poderes de\(x\) flotar alrededor y estamos tomando derivados, quizás el logaritmo (el antiderivado de\(x^{-1}\)) está alrededor también. Resulta que queremos probar otra solución de la forma

\[y_2 = \sum_{k=0}^\infty b_k x^{k+r} + (\ln x) y_1 , \nonumber \]

que en nuestro caso es

\[y_2 = \sum_{k=0}^\infty b_k x^{k+1/2} + (\ln x) x^{1/2} e^x . \nonumber \]

Ahora diferenciamos esta ecuación, sustituimos en la ecuación diferencial y resolvemos para\(b_k\). Se produce un largo cálculo y obtenemos alguna relación de recursión para\(b_k\). El lector puede (y debe) probar esto para obtener por ejemplo los tres primeros términos

\[b_1 = b_0 -1 , \qquad b_2 = \dfrac{2b_1-1}{4} , \qquad b_3 = \dfrac{6b_2-1}{18} , \qquad \ldots \nonumber \]

Luego arreglamos\(b_0\) y obtenemos una solución\(y_2\). Entonces escribimos la solución general como\(y = A y_1 + B y_2\).

Método de Frobenius

Antes de dar el método general, aclaremos cuándo aplica el método. Let

\[p(x) y'' + q(x) y' + r(x) y = 0 \nonumber \]

ser una ODE. Como antes, si\(p(x_0) = 0\), entonces\(x_0\) es un punto singular. Si, además, los límites

\[\lim_{x \to x_0} ~ (x-x_0) \dfrac{q(x)}{p(x)} \qquad \text{and} \qquad \lim_{x \to x_0} ~ (x-x_0)^2 \dfrac{r(x)}{p(x)} \nonumber \]

ambos existen y son finitos, entonces decimos que\(x_0\) es un punto singular regular.

Ejemplo\(\PageIndex{3}\): Expansion around a regular singular point

A menudo, y para el resto de esta sección,\(x_0 = 0\). Considerar

\[x^2y'' + x(1+x)y' + (\pi+x^2)y = 0 . \nonumber \]

Escribir

\[\begin{align}\begin{aligned} \lim_{x \to 0} ~x \dfrac{q(x)}{p(x)} &=\lim_{x \to 0} ~x \dfrac{x(1+x)}{x^2} = \lim_{x \to 0} ~(1+x) = 1 , \\ \lim_{x \to 0} ~x^2 \dfrac{r(x)}{p(x)} &=\lim_{x \to 0} ~x^2 frac{(\pi+x^2)}{x^2} = \lim_{x \to 0} ~(\pi+x^2) = \pi \end{aligned}\end{align}. \nonumber \]

Así\(x = 0\) es un punto singular regular.

Por otro lado si hacemos el ligero cambio

\[x^2y'' + (1+x)y' + (\pi+x^2)y = 0 , \nonumber \]

entonces

\[\lim_{x \to 0} ~x \dfrac{q(x)}{p(x)} =\lim_{x \to 0} ~x \dfrac{(1+x)}{x^2} = \lim_{x \to 0} ~\dfrac{1+x}{x} =\text{DNE}. \nonumber \]

Aquí DNE significa no existe. El punto\(0\) es un punto singular, pero no un punto singular regular.

Discutamos ahora el Método general de Frobenius \(^{1}\). Consideremos solamente el método en ese punto\(x=0\) por simplicidad. La idea principal es el siguiente teorema.

Teorema\(\PageIndex{1}\)

Método de Frobenius

Supongamos que

\[\label{eq:26} p(x) y'' + q(x) y' + r(x) y = 0 \]

tiene un punto singular regular en\(x=0\), entonces existe al menos una solución de la forma

\[y = x^r \sum_{k=0}^\infty a_k x^k . \nonumber \]

Una solución de esta forma se llama solución de tipo Frobenius.

El método generalmente se descompone así.

1. Buscamos una solución tipo Frobenius de la forma\[y = \sum_{k=0}^\infty a_k x^{k+r} . \nonumber \] Conectamos esto\(y\) en ecuación\(\eqref{eq:26}\). Recopilamos términos y escribimos todo como una sola serie.
2. La serie obtenida debe ser cero. Al establecer el primer coeficiente (generalmente el coeficiente de\(x^r\)) en la serie a cero obtenemos la ecuación indicial, que es un polinomio cuadrático en\(r\).
3. Si la ecuación indicial tiene dos raíces reales\(r_1\) y\(r_2\) tal que no\(r_1 - r_2\) es un número entero, entonces tenemos dos soluciones de tipo Frobenius linealmente independientes. Usando la primera raíz, conectamos\[y_1 = x^{r_1} \sum_{k=0}^\infty a_k x^{k} , \nonumber \] y resolvemos para\(a_k\) que todos obtengan la primera solución. Luego usando la segunda raíz, conectamos\[y_2 = x^{r_2} \sum_{k=0}^\infty b_k x^{k} , \nonumber \] y resolvemos para\(b_k\) que todos obtengan la segunda solución.
4. Si la ecuación indicial tiene una raíz duplicada\(r\), entonces ahí encontramos una solución\[y_1 = x^{r} \sum_{k=0}^\infty a_k x^{k} , \nonumber \] y luego obtenemos una nueva solución conectándonos\[y_2 = x^{r} \sum_{k=0}^\infty b_k x^{k} + (\ln x) y_1 , \nonumber \] a Ecuación\(\eqref{eq:26}\) y resolviendo las constantes\(b_k\).
5. Si la ecuación indicial tiene dos raíces reales tales que\(r_1-r_2\) es un entero, entonces una solución es\[y_1 = x^{r_1} \sum_{k=0}^\infty a_k x^{k} , \nonumber \] y la segunda solución linealmente independiente es de la forma\[y_2 = x^{r_2} \sum_{k=0}^\infty b_k x^{k} + C (\ln x) y_1 , \nonumber \] donde nos\(y_2\) conectamos\(\eqref{eq:26}\) y resolvemos para las constantes\(b_k\) y\(C\).
6. Finalmente, si la ecuación indicial tiene raíces complejas, entonces resolver para\(a_k\) en la solución\[y = x^{r_1} \sum_{k=0}^\infty a_k x^{k} \nonumber \] resulta en una función de valor complejo, todos los números\(a_k\) son complejos. Obtenemos nuestras dos soluciones linealmente independientes \(^{2}\)tomando las partes real e imaginaria de\(y\).

La idea principal es encontrar al menos una solución tipo Frobenius. Si tenemos suerte y encontramos dos, ya terminamos. Si solo conseguimos una, o bien utilizamos las ideas anteriores o incluso un método diferente como la reducción del orden (Ejercicio 2.1.8) para obtener una segunda solución.

Funciones de Bessel

Una clase importante de funciones que surge comúnmente en la física son las funciones de Bessel \(^{3}\). Por ejemplo, estas funciones aparecen al resolver la ecuación de onda en dos y tres dimensiones. Primero tenemos la ecuación de orden de Bessel\(p\):

\[x^2 y'' + xy' + \left(x^2 - p^2\right)y = 0 . \nonumber \]

Permitimos\(p\) ser cualquier número, no solo un entero, aunque los enteros y múltiplos de\(\dfrac{1}{2}\) son los más importantes en las aplicaciones. Cuando enchufamos

\[y = \sum_{k=0}^\infty a_k x^{k+r} \nonumber \]

en la ecuación de orden de Bessel\(p\) obtenemos la ecuación indicial

\[r(r-1)+r-p^2 = (r-p)(r+p) = 0 . \nonumber \]

Por lo tanto obtenemos dos raíces\(r_1 = p\) y\(r_2 = -p\). Si no\(p\) es un entero siguiendo el método de Frobenius y estableciendo\(a_0 = 1\), obtenemos soluciones linealmente independientes de la forma

\[\begin{align}\begin{aligned} y_1 &= x^p \sum_{k=0}^{\infty} \dfrac{(-1)^k x^{2k}}{2^{2k}k!(k+p)(k-1+p) \cdots (2+p)(1+p)}, \\ y_2 &= x^{-p} \sum_{k=0}^{\infty} \dfrac{(-1)^k x^{2k}}{2^{2k}k!(k-p)(k-1-p) \cdots (2-p)(1-p)}.\end{aligned}\end{align} \nonumber \]

Ejercicio\(\PageIndex{1}\)

1. Verificar que la ecuación indicial de la ecuación de orden de Bessel\(p\) es\((r-p)(r+p)=0\).
2. Supongamos que no\(p\) es un entero. Realizar el cómputo para obtener las soluciones\(y_1\) y\(y_2\) superiores.

Las funciones de Bessel serán convenientes múltiplos constantes de\(y_1\) y\(y_2\). Primero debemos definir la función gamma

\[\Gamma(x) = \int_0^\infty t^{x-1} e^{-t} \, dt . \nonumber \]

Fíjese en eso\(\Gamma(1) = 1\). La función gamma también tiene una propiedad maravillosa

\[\Gamma(x+1) = x \Gamma(x) . \nonumber \]

A partir de esta propiedad, se puede mostrar que\(\Gamma(n) = (n-1)!\) cuando\(n\) es un entero, por lo que la función gamma es una versión continua del factorial. Calculamos:

\[\begin{align}\begin{aligned} \Gamma(k+p+1)=(k+p)(k-1+p)\cdots (2+p)(1+p) \Gamma(1+p) ,\\ \Gamma(k-p+1)=(k-p)(k-1-p)\cdots (2-p)(1-p) \Gamma(1-p) .\end{aligned}\end{align} \nonumber \]

Ejercicio\(\PageIndex{2}\)

Verificar las identidades anteriores utilizando\(\Gamma(x+1) = x \Gamma(x)\).

Definimos las funciones de Bessel del primer tipo de orden\(p\) y\(-p\) como

\[\begin{align}\begin{aligned} J_p(x) &= \dfrac{1}{2^p\Gamma(1+p)} y_1=\sum_{k=0}^\infty \dfrac{{(-1)}^k}{k! \Gamma(k+p+1)}{\left(\dfrac{x}{2}\right)}^{2k+p} , \\ J_{-p}(x) &= \dfrac{1}{2^{-}\Gamma(1-p)} y_2=\sum_{k=0}^\infty \dfrac{{(-1)}^k}{k! \Gamma(k-p+1)}{\left(\dfrac{x}{2}\right)}^{2k-p} .\end{aligned}\end{align} \nonumber \]

Como estos son múltiplos constantes de las soluciones que encontramos anteriormente, ambas son soluciones a la ecuación de orden de Bessel\(p\). Las constantes se escogen para mayor comodidad.

Cuando no\(p\) es un número entero,\(J_p\) y\(J_{-p}\) son linealmente independientes. Cuando\(n\) es un entero obtenemos

\[J_n(x) =\sum_{k=0}^\infty \dfrac{{(-1)}^k}{k! (k+n)!}{\left(\dfrac{x}{2}\right)}^{2k+n} . \nonumber \]

En este caso resulta que

\[J_n(x) = {(-1)}^nJ_{-n}(x) , \nonumber \]

y así no obtenemos una segunda solución linealmente independiente. La otra solución es la llamada función Bessel de segundo tipo. Estos tienen sentido solo para órdenes enteros\(n\) y se definen como límites de combinaciones lineales de\(J_p(x)\) y\(J_{-p}(x)\) como\(p\) enfoques\(n\) de la siguiente manera:

\[Y_n(x) = \lim_{p\to n} \dfrac{\cos(p \pi) J_p(x) - J_{-p}(x)}{\sin(p \pi)} . \nonumber \]

Como cada combinación lineal de\(J_p(x)\) y\(J_{-p}(x)\) es una solución a la ecuación de orden de Bessel\(p\), entonces a medida que tomamos el límite como\(p\) va a\(n\),\(Y_n(x)\) es una solución a la ecuación de orden de Bessel\(n\). También resulta que\(Y_n(x)\) y\(J_n(x)\) son linealmente independientes. Por lo tanto, cuando\(n\) es un número entero, tenemos la solución general a la ecuación de orden de Bessel\(n\)

\[y = A J_n(x) + B Y_n(x) , \nonumber \]

para constantes arbitrarias\(A\) y\(B\). Tenga en cuenta que\(Y_n(x)\) va al infinito negativo en\(x=0\). Muchos paquetes de software matemático tienen estas funciones\(J_n(x)\) y\(Y_n(x)\) definidas, por lo que se pueden usar igual que decir\(\sin(x)\) y\(\cos(x)\). De hecho, tienen algunas propiedades similares. Por ejemplo,\(-J_1(x)\) es una derivada de\(J_0(x)\), y en general la derivada de\(J_n(x)\) puede escribirse como una combinación lineal de\(J_{n-1}(x)\) y\(J_{n+1}(x)\). Además, estas funciones oscilan, aunque no son periódicas. Consulte la Figura\(\PageIndex{1}\) para ver gráficas de las funciones de Bessel.

Figura\(\PageIndex{1}\): Gráfica de la\(J_{0}(x)\) y\(J_{1}(x)\) en la primera gráfica y\(Y_{0}(x)\) y\(Y_{1}(x)\) en la segunda gráfica.

Ejemplo\(\PageIndex{4}\): Using Bessel functions to Solve a ODE

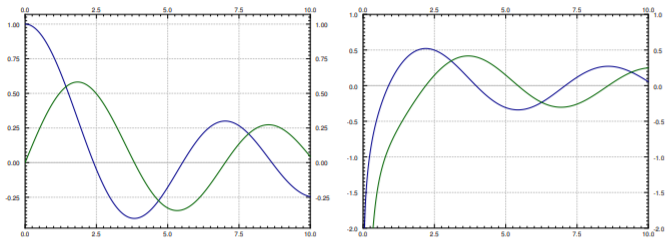
Otras ecuaciones a veces se pueden resolver en términos de las funciones de Bessel. Por ejemplo, dada una constante positiva\(\lambda\),

\[x y'' + y' + \lambda^2 x y = 0 , \nonumber \]

se puede cambiar a\(x^2 y'' + x y' + \lambda^2 x^2 y = 0\). Luego cambiando las variables\(t = \lambda x\) obtenemos a través de la regla de cadena la ecuación en\(y\) y\(t\):

\[t^2 y'' + t y' + t^2 y = 0 , \nonumber \]

que puede reconocerse como la ecuación de Bessel de orden 0. Por lo tanto, la solución general es\(y(t) = A J_0(t) + B Y_0(t)\), o en términos de\(x\):

\[y = A J_0(\lambda x) + B Y_0(\lambda x) . \nonumber \]

Esta ecuación surge por ejemplo al encontrar modos fundamentales de vibración de un tambor circular, pero nos degremos.

Notas al pie

[1] Nombrado así por el matemático alemán Ferdinand Georg Frobenius (1849 — 1917).

[2] Véase Joseph L. Neuringera, El método Frobenius para raíces complejas de la ecuación indicial, Revista Internacional de Educación Matemática en Ciencia y Tecnología, Volumen 9, Número 1, 1978, 71—77.

[3] Nombrado así por el astrónomo y matemático alemán Friedrich Wilhelm Bessel (1784 — 1846).