3.2: Condiciones explícitas de límites

Última actualización
Guardar como PDF

Page ID: 113777

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Para los problemas de interés aquí solo consideraremos condiciones límite lineales, que expresan una relación lineal entre la función y sus derivadas parciales, e.g.,\[u(x,y=0) + x \frac{\partial u}{\partial x}(x,y=0)=0. \nonumber \] Como antes el orden máximo de la derivada en la condición límite es un orden menor que el orden de la PDE. Para una ecuación diferencial de segundo orden tenemos tres posibles tipos de condición de límite

Condición de límite de Dirichlet

Cuando especificamos el valor de\(u\) en el límite, hablamos de condiciones de límite de Dirichlet. Un ejemplo para una cuerda vibratoria con sus extremos, en\(x=0\) y\(x=L\), fijos sería

\[u(0,t) = u(L,t) = 0. \nonumber \]

Condiciones de límite de von Neumann

En problemas multidimensionales la derivada de una función w.r.t. a cada una de las variables forma un campo vectorial (es decir, una función que toma un valor vectorial en cada punto del espacio), generalmente llamado gradiente. Para tres variables esto toma la forma\[\mbox{grad} \space f(x,y,z) = {\nabla} f(x,y,z) = \left (\frac{\partial f}{\partial x}(x,y,z),\frac{\partial f}{\partial y}(x,y,z),\frac{\partial f}{\partial z}(x,y,z)\right ). \nonumber \]

**Figura\(\PageIndex{1}\):** Un boceto de las derivadas normales utilizadas en las condiciones límite de von Neumann.

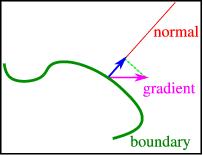
Normalmente no podemos especificar el gradiente en el límite ya que eso es demasiado restrictivo para permitir soluciones. Podemos —y en los problemas físicos a menudo es necesario— especificar el componente normal al límite, ver Figura\(\PageIndex{1}\) para un ejemplo. Cuando se especifica esta derivada normal hablamos de condiciones límite de von Neumann.

En el caso de una varilla aislada (infinitamente delgada) de longitud\(a\), no podemos tener un flujo de calor más allá de los extremos para que el gradiente de la temperatura deba desaparecer (el calor solo puede fluir donde exista una diferencia de temperatura). Esto lleva a la BC

\[\frac{\partial u}{\partial x}(0,t) = \frac{\partial u}{\partial x}(a,t) = 0. \nonumber \]

Condiciones de límite mixtas (Robin's)

Por supuesto, podemos mezclar las condiciones límite de Dirichlet y von Neumann. Para el ejemplo de varilla delgada dado anteriormente podríamos requerir

\[u(0,t) + \frac{\partial u}{\partial x}(0,t) = u(a,t) + \frac{\partial u}{\partial x}(a,t) = 0. \nonumber \]