10.7: Nuestro problema inicial y funciones de Bessel

Última actualización
Guardar como PDF

Page ID: 113668

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Comenzamos la discusión a partir del problema de la temperatura en un disco circular, resuelto en coordenadas polares, ya que las condiciones iniciales no dependen de\(\phi\), esperamos que la solución sea radialmente simétrica también,\(u(\rho,t)\), lo que satisface la ecuación

\[\begin{aligned} \frac{\partial u}{\partial t} &= k\left[ \frac{\partial^2 u}{\partial \rho^2} + \frac{1}{\rho} \frac{\partial u}{\partial \rho} \right],\nonumber\\ u(c,t) &=0,\nonumber\\ u(\rho,0) &= f(\rho).\end{aligned} \nonumber \]

Con\(u(\rho,t)=R(\rho)T(t)\) encontramos las ecuaciones

\[\begin{aligned} \rho^2 R''+\rho R' + \lambda \rho^2 R &= 0\;\;\;\;R(c)=0\nonumber\\ T'+\lambda k T = 0.\end{aligned} \nonumber \]

La ecuación para\(R\) es claramente autounida, se puede escribir como

\[[\rho R']' + \lambda \rho R = 0 \nonumber \]

Entonces, ¿cómo se\(R\) relaciona la ecuación para con la ecuación de Bessel? Hagamos el cambio de variables\(x= \sqrt{\lambda} \rho\). ENCONTRAMOS

\[\frac{d}{d\rho} = \sqrt{\lambda} \frac{d}{dx}, \nonumber \]

y podemos eliminar un factor común\(\sqrt{\lambda}\) para obtener (\(X(x)=R(\rho)\))

\[[x X']' + x X = 0, \nonumber \]

que es la ecuación de orden de Bessel\(0\), es decir,

\[R(\rho) = J_0(\rho \sqrt{\lambda}). \nonumber \]

La condición de límite\(R(c)=0\) muestra que\[c \sqrt{\lambda_n} = x_n, \nonumber \]

donde\(x_n\) están los puntos donde\(J_0(x)=0\). Concluimos así que\[R_n(\rho) = J_0(\rho \sqrt{\lambda_n}). \nonumber \] las primeras cinco soluciones\(R_n\) (para\(c=1\)) se muestran en la Fig. \(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Una gráfica de las cinco primeras funciones\(R_n\)

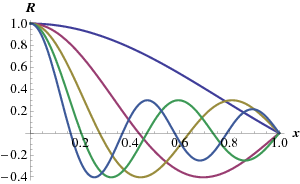
De la teoría de Sturm-Liouville concluimos que

\[\int_0^\infty \rho d\rho \,R_n(\rho)R_m(\rho)=0\;\;{\rm if\ }n \neq m. \nonumber \]

Junto con la solución para la\(T\) ecuación,

\[T_n(t)= \exp(-\lambda_n k t) \nonumber \]

encontramos una solución tipo serie Fourier-Bessel

\[u(\rho,t) = \sum_{n=1}^\infty A_n J_0(\rho\sqrt{\lambda_n})\exp(-\lambda_n k t), \nonumber \]

con\(\lambda_n= (x_n/c)^2\).

Para entender cómo determinar los coeficientes a\(A_n\) partir de la condición inicial\(u(\rho,0)=f(\rho)\) necesitamos estudiar las series de Fourier-Bessel con un poco más de detalle.