15.1: Finalización Proyectiva

Última actualización
Guardar como PDF

Page ID: 114694

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En el plano euclidiano, dos líneas distintas podrían tener uno o cero puntos de intersección (en este último caso las líneas son paralelas). Nuestro objetivo es extender el plano euclidiano por puntos ideales para que dos líneas distintas tengan exactamente un punto de intersección.

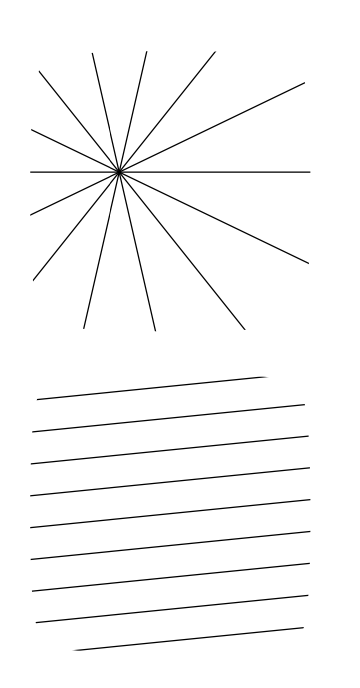
$2021-02-25 2.01.13.png$

Una colección de líneas en el plano euclidiano se llama concurrente si todas se cruzan en un solo punto o todas ellas paralelas por pares. Un conjunto máximo de líneas concurrentes en el plano se llama lápiz. Hay dos tipos de lápices: los lápices centrales contienen todas las líneas que pasan a través de un punto fijo llamado centro del lápiz y el lápiz paralelo contiene líneas paralelas por pares.

Cada punto en el plano euclidiano define de manera única un lápiz central con el centro en él. Tenga en cuenta que dos líneas cualesquiera determinan completamente el lápiz que contiene ambas.

Añadamos un punto ideal para cada lápiz paralelo, y supongamos que todos estos puntos ideales se encuentran en una línea ideal. También asumimos que la línea ideal pertenece a cada lápiz paralelo.

Obtenemos el llamado plano proyectivo real, o terminación proyectiva del plano original. Viene con una estructura de incidencia —decimos que tres puntos se encuentran en una línea si los lápices correspondientes contienen una línea común. La geometría proyectiva estudia esta estructura de incidencia.

Describamos los puntos de terminación proyectiva en coordenadas. Un lápiz paralelo contiene la línea ideal y las líneas$y = m \cdot x+b$ con pendiente fija$m$; si$m=\infty$, suponemos que las líneas están dadas por ecuaciones$x=a$. Por lo tanto, el plano proyectivo real contiene cada punto$(x,y)$ en el plano de coordenadas más la línea ideal que contiene un punto ideal$P_m$ para cada pendiente$m \in \mathbb{R} \cup \{\infty\}$.