Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

16.5: Proyección central

Última actualización

30 oct 2022
Guardar como PDF
- 16.4: Proyección estereográfica
- 17: Modelo Proyectivo

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

La proyección central es análoga al modelo proyectivo del plano hiperbólico que se discute en el Capítulo 17.

$\Sigma$ Sea la esfera unitaria centrada en el origen que será denotada por $O$ . Supongamos que $\Pi^+$ denota el plano definido por la ecuación $z=1$ . Este plano es paralelo al $xy$ plano y pasa por el polo norte $N =(0,0,1)$ de $\Sigma$ .

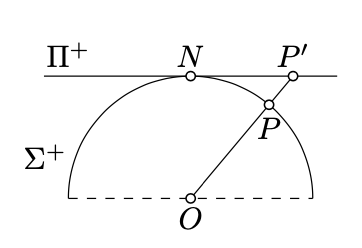
$2021-03-01 10.34.45.png$

Recordemos que el hemisferio norte de $\Sigma$ , es el subconjunto de puntos $(x,y,z)\in \Sigma$ tales que $z>0$ . El hemisferio norte será denotado por $\Sigma^+$ .

Dado un punto $P\in \Sigma^+$ , considere la media línea $[OP)$ . Supongamos que $P'$ denota la intersección de $[OP)$ y $\Pi^+$ . Tenga en cuenta que si $P=(x,y,z)$ , entonces $P'=(\dfrac{x}{z},\dfrac{y}{z},1)$ . De ello se deduce que $P\leftrightarrow P'$ es una bijección entre $\Sigma^+$ y $\Pi^+$ .

La biyección descrita $\Sigma^+ \leftrightarrow \Pi^+$ se denomina proyección central del hemisferio $\Sigma^+$ .

Tenga en cuenta que la proyección central envía las intersecciones de los grandes círculos con $\Sigma^+$ a las líneas en $\Pi^+$ . Esto último sigue ya que los grandes círculos son intersecciones de $\Sigma$ con planos que pasan por el origen así como las líneas en $\Pi^+$ son la intersección de $\Pi^+$ con estos planos.

El siguiente ejercicio es análogo al Ejercicio 17.2.1 en geometría hiperbólica.

Ejercicio $\PageIndex{1}$

Dejar $\triangle_sABC$ ser un triángulo esférico no degenerado. Supongamos que el plano $\Pi^+$ es paralelo al plano que pasa a través de $A$ $B$ ,, y $C$ . Dejar $A'$ , $B'$ , y $C'$ denotar las proyecciones centrales de $A$ , $B$ y $C$ .

Mostrar que los puntos medios de $[A'B']$ , $[B'C']$ , y $[C'A']$ son proyecciones centrales de los puntos medios de $[AB]_s$ $[BC]_s$ , y $[CA]_s$ respectivamente.
Utilice la parte (a) para mostrar que las medianas de un triángulo esférico se cruzan en un punto.

Pista

a). Observe y use eso $OA' = OB' = OC'$ .

b). Tenga en cuenta que las medianas del triángulo esférico ABC mapean a las medianas de Euclides un triángulo $A'B'C'$ . Queda por aplicar el Teorema 8.3.1 para $\triangle A'B'C'$ .

Ejercicio16.5.1\PageIndex{1}

Support Center

How can we help?

Ejercicio $\PageIndex{1}$