2.3: Las leyes de límite
- Page ID
- 116797
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Reconocer las leyes básicas de límite.
- Utilizar las leyes de límite para evaluar el límite de una función.
- Evaluar el límite de una función por factorización.
- Utilizar las leyes de límite para evaluar el límite de una función polinómica o racional.
- Evaluar el límite de una función factorizando o usando conjugados.
- Evaluar el límite de una función usando el teorema squeeze.
En la sección anterior, evaluamos límites mirando gráficos o construyendo una tabla de valores. En esta sección, establecemos leyes para el cálculo de límites y aprendemos a aplicarlas. En el Proyecto Estudiantil al final de esta sección, tienes la oportunidad de aplicar estas leyes de limitación para derivar la fórmula para el área de un círculo adaptando un método ideado por el matemático griego Arquímedes. Comenzamos por replantear dos resultados límite útiles de la sección anterior. Estos dos resultados, junto con las leyes de límites, sirven de base para calcular muchos límites.
Evaluar los límites con las leyes de límite
Las dos primeras leyes de limitación fueron declaradas previamente y aquí las repetimos. Estos resultados básicos, junto con las otras leyes de límite, nos permiten evaluar los límites de muchas funciones algebraicas.
Para cualquier número real\(a\) y cualquier constante\(c\),
- \(\displaystyle \lim_{x→a}x=a\)
- \(\displaystyle \lim_{x→a}c=c\)
Evalúe cada uno de los siguientes límites usando “Resultados de Límite Básico”.
- \(\displaystyle \lim_{x→2}x\)
- \(\displaystyle \lim_{x→2}5\)
Solución
- El límite de\(x\) lo que se\(x\) aproxima\(a\) es\(a\):\(\displaystyle \lim_{x→2}x=2\).
- El límite de una constante es esa constante:\(\displaystyle \lim_{x→2}5=5\).
Ahora echamos un vistazo a las leyes de límites, las propiedades individuales de los límites. Aquí se omiten las pruebas que tienen estas leyes.
Dejar\(f(x)\) y\(g(x)\) ser definido para todo\(x≠a\) lo largo de algún intervalo abierto que contiene\(a\). Supongamos que\(L\) y\(M\) son números reales tales que\(\displaystyle \lim_{x→a}f(x)=L\) y\(\displaystyle \lim_{x→a}g(x)=M\). Que\(c\) sea una constante. Entonces, cada una de las siguientes declaraciones sostiene:
- Ley de suma para límites:
\[\displaystyle \lim_{x→a}(f(x)+g(x))=\lim_{x→a}f(x)+\lim_{x→a}g(x)=L+M \nonumber \]
- Ley de diferencia para límites:
\[\displaystyle \lim_{x→a}(f(x)−g(x))=\lim_{x→a}f(x)−\lim_{x→a}g(x)=L−M \nonumber \]
- Ley múltiple constante para límites:
\[\displaystyle \lim_{x→a}cf(x)=c⋅\lim_{x→a}f(x)=cL \nonumber \]
- Ley de producto para límites:
\[\displaystyle \lim_{x→a}(f(x)⋅g(x))=\lim_{x→a}f(x)⋅\lim_{x→a}g(x)=L⋅M \nonumber \]
- Ley de cocientes para límites:
\[\displaystyle \lim_{x→a}\frac{f(x)}{g(x)}=\frac{\displaystyle \lim_{x→a}f(x)}{\displaystyle \lim_{x→a}g(x)}=\frac{L}{M} \nonumber \]
para\(M≠0\).
- Ley de poder para límites:
\[\displaystyle \lim_{x→a}\big(f(x)\big)^n=\big(\lim_{x→a}f(x)\big)^n=L^n \nonumber \]
por cada entero positivo\(n\).
- Ley raíz para límites:
\[\displaystyle \lim_{x→a}\sqrt[n]{f(x)}=\sqrt[n]{\lim_{x→a} f(x)}=\sqrt[n]{L} \nonumber \]
para todos\(L\) si\(n\) es impar y para\(L≥0\) si\(n\) es par.
Ahora practicamos aplicar estas leyes de limitación para evaluar un límite.
Utilizar las leyes de límite para evaluar\[\lim_{x→−3}(4x+2). \nonumber \]
Solución
Apliquemos las leyes de límite paso a paso para asegurarnos de que entendemos cómo funcionan. Debemos tener presente el requisito de que, en cada aplicación de una ley de límites, deben existir los nuevos límites para que se aplique la ley de límites.
\[\begin{align*} \lim_{x→−3}(4x+2) &= \lim_{x→−3} 4x + \lim_{x→−3} 2 & & \text{Apply the sum law.}\\[4pt] &= 4⋅\lim_{x→−3} x + \lim_{x→−3} 2 & & \text{Apply the constant multiple law.}\\[4pt] &= 4⋅(−3)+2=−10. & & \text{Apply the basic limit results and simplify.} \end{align*}\]
Utilizar las leyes de límite para evaluar\[\lim_{x→2}\frac{2x^2−3x+1}{x^3+4}. \nonumber \]
Solución
Para encontrar este límite, necesitamos aplicar las leyes de límite varias veces. Nuevamente, hay que tener en cuenta que a medida que reescribimos el límite en términos de otros límites, cada nuevo límite debe existir para que se aplique la ley de límites.
\ [\ begin {align*}\ lim_ {x→2}\ frac {2x^2−3x+1} {x^3+4} &=\ frac {\ displaystyle\ lim_ {x→2} (2x^2−3x+1)} {\ displaystyle\ lim_ {x→2} (x^3+4)} &\ text {Aplica la ley del cociente, asegúrate de que} (2) ^3+4≠ 0.\\ [4pt]
&=\ frac {\ displaystyle 2⋅\ lim_ {x→2} x^2−3⋅\ lim_ {x→2} x+\ lim_ {x→2} 1} {\ displaystyle\ lim_ {x→ 2} x^3+\ lim_ {x→2} 4} &\ text {Aplica la ley de suma y la ley múltiple constante.}\\ [4pt]
&=\ frac {\ displaystyle 2⋅\ left (\ lim_ {x→2} x\ derecha) ^2−3⋅\ lim_ {x→2} x+\ lim_ {x→2} 1} {\ displaystyle\ izquierda (\ lim_ {x→2} x\ derecha) ^3+\ lim_ {x→2} 4} &\ text {Aplicar la ley de poder.}\\ [4pt]
&=\ frac {2 (4) −3 (2) +1} {(2) ^3+4} =\ frac {1} {4}. & &\ text {Aplicar las leyes básicas de límite y simplificar.} \ end {alinear*}\]
Utilice las leyes de límite para evaluar\(\displaystyle \lim_{x→6}(2x−1)\sqrt{x+4}\). En cada paso, indicar la ley límite aplicada.
- Pista
-
Empezar por aplicar la ley de producto.
- Contestar
-
\(11\sqrt{10}\)
Técnicas de Evaluación de Límites Adicionales
Como hemos visto, podemos evaluar fácilmente los límites de polinomios y los límites de algunas (pero no todas) funciones racionales por sustitución directa. No obstante, como vimos en la sección introductoria sobre límites, ciertamente es posible\(\displaystyle \lim_{x→a}f(x)\) que exista cuando\(f(a)\) está indefinido. La siguiente observación nos permite evaluar muchos límites de este tipo:
Si por todo\(x≠a,\;f(x)=g(x)\) lo largo de algún intervalo abierto que contiene\(a\), entonces
\[\displaystyle\lim_{x→a}f(x)=\lim_{x→a}g(x). \nonumber \]
Para entender mejor esta idea, considera el límite\(\displaystyle \lim_{x→1}\dfrac{x^2−1}{x−1}\).
La función
\[f(x)=\dfrac{x^2−1}{x−1}=\dfrac{(x−1)(x+1)}{x−1}\nonumber \]
y la función\(g(x)=x+1\) son idénticos para todos los valores de\(x≠1\). Las gráficas de estas dos funciones se muestran en la Figura\(\PageIndex{1}\).
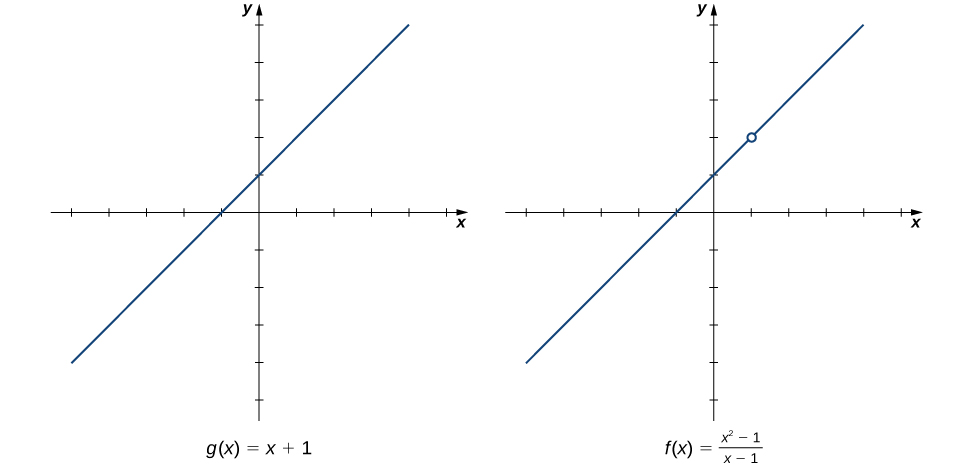
Vemos que
\[\lim_{x→1}\dfrac{x^2−1}{x−1}=\lim_{x→1}\dfrac{(x−1)(x+1)}{x−1}=\lim_{x→1}\,(x+1)=2.\nonumber \]
El límite tiene la forma\(\displaystyle \lim_{x→a}f(x)/g(x)\), dónde\(\displaystyle\lim_{x→a}f(x)=0\) y\(\displaystyle\lim_{x→a}g(x)=0\). (En este caso, decimos que\(f(x)/g(x)\) tiene la forma indeterminada\(0/0\).) La siguiente Estrategia de Resolución de Problemas proporciona un esquema general para evaluar límites de este tipo.
- Primero, debemos asegurarnos de que nuestra función tenga la forma adecuada y no pueda ser evaluada inmediatamente usando las leyes de límite.
- Entonces necesitamos encontrar una función que sea igual a\(h(x)=f(x)/g(x)\) para todo\(x≠a\) lo largo de algún intervalo que contenga a. para ello, es posible que tengamos que probar uno o más de los siguientes pasos:
- Si\(f(x)\) y\(g(x)\) son polinomios, debemos factorizar cada función y cancelar cualquier factor común.
- Si el numerador o denominador contiene una diferencia que involucra una raíz cuadrada, deberíamos intentar multiplicar el numerador y el denominador por el conjugado de la expresión que involucra a la raíz cuadrada.
- Si\(f(x)/g(x)\) es una fracción compleja, comenzamos por simplificarla.
- Por último, aplicamos las leyes de límite.
Los siguientes ejemplos demuestran el uso de esta Estrategia de Resolución de Problemas. Ejemplo\(\PageIndex{4}\) ilustra la técnica de factor y cancelación; Ejemplo\(\PageIndex{5}\) muestra multiplicar por un conjugado. En Ejemplo\(\PageIndex{6}\), nos fijamos en simplificar una fracción compleja.
Evaluar\(\displaystyle\lim_{x→3}\dfrac{x^2−3x}{2x^2−5x−3}\).
Solución
Paso 1. La función no\(f(x)=\dfrac{x^2−3x}{2x^2−5x−3}\) está definida para\(x=3\). De hecho, si sustituimos 3 en la función obtenemos\(0/0\), que no está definida. Factorizar y cancelar es una buena estrategia:
\[\lim_{x→3}\dfrac{x^2−3x}{2x^2−5x−3}=\lim_{x→3}\dfrac{x(x−3)}{(x−3)(2x+1)}\nonumber \]
Paso 2. Para todos\(x≠3,\dfrac{x^2−3x}{2x^2−5x−3}=\dfrac{x}{2x+1}\). Por lo tanto,
\[\lim_{x→3}\dfrac{x(x−3)}{(x−3)(2x+1)}=\lim_{x→3}\dfrac{x}{2x+1}.\nonumber \]
Paso 3. Evaluar usando las leyes de límite:
\[\lim_{x→3}\dfrac{x}{2x+1}=\dfrac{3}{7}.\nonumber \]
Evaluar\(\displaystyle \lim_{x→−3}\dfrac{x^2+4x+3}{x^2−9}\).
- Pista
-
Siga los pasos de la estrategia de resolución de problemas
- Contestar
-
\(\dfrac{1}{3}\)
Evaluar\( \displaystyle \lim_{x→−1}\dfrac{\sqrt{x+2}−1}{x+1}\).
Solución
Paso 1. \( \displaystyle \dfrac{\sqrt{x+2}−1}{x+1}\)tiene la forma\(0/0\) en −1. Empecemos multiplicando por\(\sqrt{x+2}+1\), el conjugado de\(\sqrt{x+2}−1\), sobre el numerador y denominador:
\[\lim_{x→−1}\dfrac{\sqrt{x+2}−1}{x+1}=\lim_{x→−1}\dfrac{\sqrt{x+2}−1}{x+1}⋅\dfrac{\sqrt{x+2}+1}{\sqrt{x+2}+1}.\nonumber \]
Paso 2. Luego multiplicamos el numerador. No multiplicamos el denominador porque estamos esperando que el\((x+1)\) en el denominador se cancele al final:
\[=\lim_{x→−1}\dfrac{x+1}{(x+1)(\sqrt{x+2}+1)}.\nonumber \]
Paso 3. Luego cancelamos:
\[= \lim_{x→−1}\dfrac{1}{\sqrt{x+2}+1}.\nonumber \]
Paso 4. Por último, aplicamos las leyes de límite:
\[\lim_{x→−1}\dfrac{1}{\sqrt{x+2}+1}=\dfrac{1}{2}.\nonumber \]
Evaluar\( \displaystyle \lim_{x→5}\dfrac{\sqrt{x−1}−2}{x−5}\).
- Pista
-
Siga los pasos de la estrategia de resolución de problemas
- Contestar
-
\(\dfrac{1}{4}\)
Evaluar\( \displaystyle \lim_{x→1}\dfrac{\dfrac{1}{x+1}−\dfrac{1}{2}}{x−1}\).
Solución
Paso 1. \(\dfrac{\dfrac{1}{x+1}−\dfrac{1}{2}}{x−1}\)tiene el formulario\(0/0\) en 1. Simplificamos la fracción algebraica multiplicando por\(2(x+1)/2(x+1)\):
\[\lim_{x→1}\dfrac{\dfrac{1}{x+1}−\dfrac{1}{2}}{x−1}=\lim_{x→1}\dfrac{\dfrac{1}{x+1}−\dfrac{1}{2}}{x−1}⋅\dfrac{2(x+1)}{2(x+1)}.\nonumber \]
Paso 2. A continuación, multiplicamos a través de los numeradores. No multiplicar los denominadores porque queremos poder cancelar el factor\((x−1)\):
\[=\lim_{x→1}\dfrac{2−(x+1)}{2(x−1)(x+1)}.\nonumber \]
Paso 3. Luego, simplificamos el numerador:
\[=\lim_{x→1}\dfrac{−x+1}{2(x−1)(x+1)}.\nonumber \]
Paso 4. Ahora facetamos −1 del numerador:
\[=\lim_{x→1}\dfrac{−(x−1)}{2(x−1)(x+1)}.\nonumber \]
Paso 5. Luego, cancelamos los factores comunes de\((x−1)\):
\[=\lim_{x→1}\dfrac{−1}{2(x+1)}.\nonumber \]
Paso 6. Por último, evaluamos usando las leyes de límite:
\[\lim_{x→1}\dfrac{−1}{2(x+1)}=−\dfrac{1}{4}.\nonumber \]
Evaluar\( \displaystyle \lim_{x→−3}\dfrac{\dfrac{1}{x+2}+1}{x+3}\).
- Pista
-
Siga los pasos de la estrategia de resolución de problemas
- Contestar
-
−1
\(\PageIndex{7}\)El ejemplo no cae pulcramente en ninguno de los patrones establecidos en los ejemplos anteriores. Sin embargo, con un poco de creatividad, todavía podemos usar estas mismas técnicas.
Evaluar\( \displaystyle \lim_{x→0}\left(\dfrac{1}{x}+\dfrac{5}{x(x−5)}\right)\).
Solución:
Ambos\(1/x\) y\(5/x(x−5)\) no logran tener un límite a cero. Dado que ninguna de las dos funciones tiene un límite en cero, no podemos aplicar la ley de suma para los límites; debemos usar una estrategia diferente. En este caso, encontramos el límite realizando suma y luego aplicando una de nuestras estrategias anteriores. Observe que
\[\dfrac{1}{x}+\dfrac{5}{x(x−5)}=\dfrac{x−5+5}{x(x−5)}=\dfrac{x}{x(x−5)}.\nonumber \]
Por lo tanto,
\[\lim_{x→0}\left(\dfrac{1}{x}+\dfrac{5}{x(x−5)}\right)=\lim_{x→0}\dfrac{x}{x(x−5)}=\lim_{x→0}\dfrac{1}{x−5}=−\dfrac{1}{5}.\nonumber \]
Evaluar\( \displaystyle \lim_{x→3}\left(\dfrac{1}{x−3}−\dfrac{4}{x^2−2x−3}\right)\).
- Pista
-
Utilice la misma técnica que Ejemplo\(\PageIndex{7}\). No olvides factorizar\(x^2−2x−3\) antes de obtener un denominador común.
- Contestar
-
\(\dfrac{1}{4}\)
Ahora volvamos a visitar los límites unilaterales. Las modificaciones simples en las leyes de límite nos permiten aplicarlas a límites unilaterales. Por ejemplo, para aplicar las leyes de límite a un límite de la forma\(\displaystyle \lim_{x→a^−}h(x)\), requerimos que la función\(h(x)\) se defina sobre un intervalo abierto de la forma\((b,a)\); para un límite de la forma\(\displaystyle \lim_{x→a^+}h(x)\), requerimos que la función\(h(x)\) se defina sobre un intervalo abierto de la forma\((a,c)\). Ejemplo\(\PageIndex{8A}\) ilustra este punto.
Evaluar cada uno de los siguientes límites, si es posible.
- \(\displaystyle \lim_{x→3^−}\sqrt{x−3}\)
- \( \displaystyle \lim_{x→3^+}\sqrt{x−3}\)
Solución
La figura\(\PageIndex{2}\) ilustra la función\(f(x)=\sqrt{x−3}\) y ayuda en nuestra comprensión de estos límites.
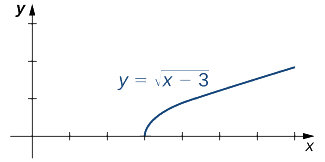
a. La función\(f(x)=\sqrt{x−3}\) se define a lo largo del intervalo\([3,+∞)\). Dado que esta función no está definida a la izquierda de 3, no podemos aplicar las leyes de límite para calcular\(\displaystyle\lim_{x→3^−}\sqrt{x−3}\). De hecho, ya que\(f(x)=\sqrt{x−3}\) está indefinido a la izquierda de 3,\(\displaystyle\lim_{x→3^−}\sqrt{x−3}\) no existe.
b. ya que\(f(x)=\sqrt{x−3}\) se define al derecho de 3, las leyes de límite sí se aplican a\(\displaystyle\lim_{x→3^+}\sqrt{x−3}\). Al aplicar estas leyes de límite obtenemos\(\displaystyle\lim_{x→3^+}\sqrt{x−3}=0\).
En Ejemplo\(\PageIndex{8B}\) observamos los límites unilaterales de una función definida por partes y usamos estos límites para sacar una conclusión sobre un límite bilateral de la misma función.
Para\(f(x)=\begin{cases}4x−3, & \mathrm{if} \; x<2 \\ (x−3)^2, & \mathrm{if} \; x≥2\end{cases}\), evaluar cada uno de los siguientes límites:
- \(\displaystyle \lim_{x→2^−}f(x)\)
- \(\displaystyle \lim_{x→2^+}f(x)\)
- \(\displaystyle \lim_{x→2}f(x)\)
Solución
La figura\(\PageIndex{3}\) ilustra la función\(f(x)\) y ayuda en nuestra comprensión de estos límites.
a. ya que\(f(x)=4x−3\) para todos\(x\) en\((−∞,2)\), sustituir\(f(x)\) en el límite por\(4x−3\) y aplicar las leyes de límite:
\[\lim_{x→2^−}f(x)=\lim_{x→2^−}(4x−3)=5\nonumber \]
b. ya que\(f(x)=(x−3)^2\) para todos\(x\) en\((2,+∞)\), sustituir\(f(x)\) en el límite por\((x−3)^2\) y aplicar las leyes de límite:
\[\lim_{x→2^+}f(x)=\lim_{x→2^−}(x−3)^2=1. \nonumber \]
c. Desde\(\displaystyle \lim_{x→2^−}f(x)=5\) y\(\displaystyle \lim_{x→2^+}f(x)=1\), concluimos que\(\displaystyle \lim_{x→2}f(x)\) no existe.
Graficar\(f(x)=\begin{cases}−x−2, & \mathrm{if} \; x<−1\\ 2, & \mathrm{if} \; x=−1 \\ x^3, & \mathrm{if} \; x>−1\end{cases}\) y evaluar\(\displaystyle \lim_{x→−1^−}f(x)\).
- Pista
-
Utilice el método en Ejemplo\(\PageIndex{8B}\) para evaluar el límite.
- Contestar
-
-1, que cruzó el eje x y el eje y en el origen." src="https://math.libretexts.org/@api/dek...02_03_004.jpeg">
\[\lim_{x→−1^−}f(x)=−1\nonumber \]
Pasamos ahora nuestra atención a evaluar un límite de la forma\(\displaystyle \lim_{x→a}\dfrac{f(x)}{g(x)}\), dónde\(\displaystyle \lim_{x→a}f(x)=K\), dónde\(K≠0\) y\(\displaystyle \lim_{x→a}g(x)=0\). Es decir,\(f(x)/g(x)\) tiene la forma\(K/0,K≠0\) en\(a\).
Evaluar\(\displaystyle \lim_{x→2^−}\dfrac{x−3}{x^2−2x}\).
Solución
Paso 1. Después de sustituir en\(x=2\), vemos que este límite tiene la forma\(−1/0\). Es decir, a medida que\(x\) se acerca\(2\) desde la izquierda, se acerca el numerador\(−1\); y se acerca el denominador\(0\). En consecuencia, la magnitud de\(\dfrac{x−3}{x(x−2)} \) se vuelve infinita. Para tener una mejor idea de cuál es el límite, necesitamos factorizar el denominador:
\[\lim_{x→2^−}\dfrac{x−3}{x^2−2x}=\lim_{x→2^−}\dfrac{x−3}{x(x−2)} \nonumber \]
Paso 2. Dado que\(x−2\) es la única parte del denominador que es cero cuando se sustituye 2, luego nos\(1/(x−2)\) separamos del resto de la función:
\[=\lim_{x→2^−}\dfrac{x−3}{x}⋅\dfrac{1}{x−2} \nonumber \]
Paso 3. Usando las Leyes de Límite, podemos escribir:
\[=\left(\lim_{x→2^−}\dfrac{x−3}{x}\right)\cdot\left(\lim_{x→2^−}\dfrac{1}{x−2}\right). \nonumber \]
Paso 4. \(\displaystyle \lim_{x→2^−}\dfrac{x−3}{x}=−\dfrac{1}{2}\)y\(\displaystyle \lim_{x→2^−}\dfrac{1}{x−2}=−∞\). Por lo tanto, el producto de\((x−3)/x\) y\(1/(x−2)\) tiene un límite de\(+∞\):
\[\lim_{x→2^−}\dfrac{x−3}{x^2−2x}=+∞. \nonumber \]
Evaluar\(\displaystyle \lim_{x→1}\dfrac{x+2}{(x−1)^2}\).
- Solución
-
Usa los métodos de Example\(\PageIndex{9}\).
- Contestar
-
\(+∞\)
El teorema del apretón
Las técnicas que hemos desarrollado hasta ahora funcionan muy bien para las funciones algebraicas, pero aún no podemos evaluar los límites de funciones trigonométricas muy básicas. El siguiente teorema, llamado teorema squeeze, resulta muy útil para establecer límites trigonométricos básicos. Este teorema nos permite calcular límites “apretando” una función, con un límite en un punto\(a\) que es desconocido, entre dos funciones que tienen un límite común conocido en\(a\). La figura\(\PageIndex{4}\) ilustra esta idea.
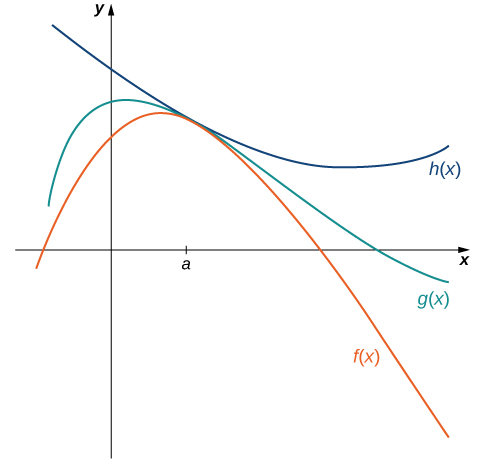
Let\(f(x),g(x)\), y\(h(x)\) ser definido para todo\(x≠a\) lo largo de un intervalo abierto que contiene\(a\). Si
\[f(x)≤g(x)≤h(x) \nonumber \]
para todos\(x≠a\) en un intervalo abierto que contiene\(a\) y
\[\lim_{x→a}f(x)=L=\lim_{x→a}h(x) \nonumber \]
donde\(L\) es un número real, entonces\(\displaystyle \lim_{x→a}g(x)=L.\)
Aplicar el teorema de squeeze para evaluar\(\displaystyle \lim_{x→0} x \cos x\).
Solución
Porque\(−1≤\cos x≤1\) para todos\(x\), tenemos\(−x≤x \cos x≤x\) para\(x≥0\) y\(−x≥x \cos x ≥ x\) para\(x≤0\) (si\(x\) es negativo la dirección de las desigualdades cambia cuando nos multiplicamos). Ya que\(\displaystyle \lim_{x→0}(−x)=0=\lim_{x→0}x\), a partir del teorema squeeze, obtenemos\(\displaystyle \lim_{x→0}x \cos x=0\). Las gráficas de\(f(x)=−x,\;g(x)=x\cos x\), y\(h(x)=x\) se muestran en la Figura\(\PageIndex{5}\).
Utilice el teorema de squeeze para evaluar\(\displaystyle \lim_{x→0}x^2 \sin\dfrac{1}{x}\).
- Pista
-
Usa el hecho de que\(−x^2≤x^2\sin (1/x) ≤ x^2\) para ayudarte a encontrar dos funciones tal que\(x^2\sin (1/x)\) se aprieta entre ellas.
- Contestar
-
0
Ahora usamos el teorema de squeeze para abordar varios límites muy importantes. Si bien esta discusión es algo larga, estos límites resultan invaluables para el desarrollo del material tanto en la siguiente sección como en el siguiente capítulo. El primero de estos límites es\(\displaystyle \lim_{θ→0}\sin θ\). Considere el círculo unitario que se muestra en la Figura\(\PageIndex{6}\). En la figura, vemos que\(\sin θ\) es la\(y\) coordenada -en el círculo unitario y corresponde al segmento de línea que se muestra en azul. La medida radianes del ángulo\(θ\) es la longitud del arco que subtiende en el círculo unitario. Por lo tanto, vemos que para\(0<θ<\dfrac{π}{2},\) tenemos\(0<\sin θ<θ.\)
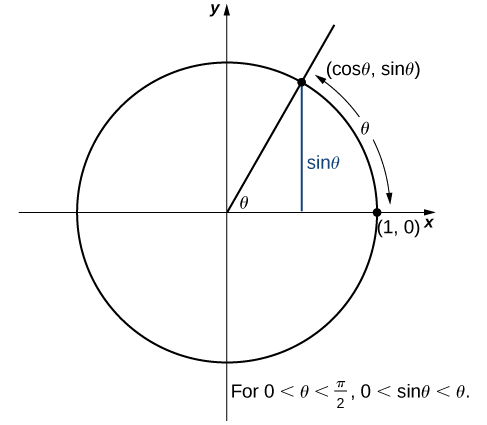
Porque\(\displaystyle \lim_{θ→0^+}0=0\) y\(\displaystyle \lim_{x→0^+}θ=0\), usando el teorema squeeze concluimos que
\[\lim_{θ→0^+}\sin θ=0.\nonumber \]
Para ver eso\(\displaystyle \lim_{θ→0^−}\sin θ=0\) también, observen eso para\(−\dfrac{π}{2}<θ<0,0<−θ<\dfrac{π}{2}\) y por lo tanto,\(0<\sin(−θ)<−θ\). En consecuencia,\(0<−\sin θ<−θ\). De ello se deduce que\(0>\sin θ>θ\). Una aplicación del teorema squeeze produce el límite deseado. Por lo tanto, desde\(\displaystyle \lim_{θ→0^+}\sin θ=0\) y\(\displaystyle \lim_{θ→0^−}\sin θ=0\),
\[\lim_{θ→0}\sin θ=0\nonumber \]
A continuación, usando la identidad\(\cos θ=\sqrt{1−\sin^2θ}\) para\(−\dfrac{π}{2}<θ<\dfrac{π}{2}\), vemos que
\[\lim_{θ→0}\cos θ=\lim_{θ→0}\sqrt{1−\sin^2θ}=1.\nonumber \]
Ahora echamos un vistazo a un límite que juega un papel importante en los capítrosposteriores, a saber,\(\displaystyle \lim_{θ→0}\dfrac{\sin θ}{θ}\). Para evaluar este límite, utilizamos el círculo unitario en la Figura\(\PageIndex{7}\). Observe que esta cifra agrega un triángulo adicional a la Figura\(\PageIndex{6}\). Vemos que la longitud del lado opuesto al ángulo\(θ\) en este nuevo triángulo es\(\tan θ\). Así, vemos que para\(0<θ<\dfrac{π}{2}\), tenemos\(\sin θ<θ<\tanθ\).
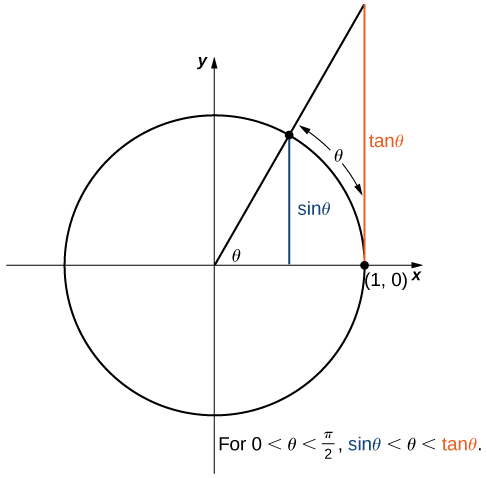
Dividiendo por\(\sin θ\) en todas las partes de la desigualdad, obtenemos
\[1<\dfrac{θ}{\sin θ}<\dfrac{1}{\cos θ}.\nonumber \]
Equivalentemente, tenemos
\[1>\dfrac{\sin θ}{θ}>\cos θ.\nonumber \]
Ya que\(\displaystyle \lim_{θ→0^+}1=1=\lim_{θ→0^+}\cos θ\), concluimos que\(\displaystyle \lim_{θ→0^+}\dfrac{\sin θ}{θ}=1\), por el teorema de squeeze. Al aplicar una manipulación similar a la utilizada para\(\displaystyle \lim_{θ→0^−}\sin θ=0\) demostrarlo, podemos demostrarlo\(\displaystyle \lim_{θ→0^−}\dfrac{\sin θ}{θ}=1\). Por lo tanto,
\[\lim_{θ→0}\dfrac{\sin θ}{θ}=1. \nonumber \]
En Ejemplo\(\PageIndex{11}\), utilizamos este límite para establecer\(\displaystyle \lim_{θ→0}\dfrac{1−\cos θ}{θ}=0\). Este límite también resulta útil en capítulos posteriores.
Evaluar\(\displaystyle \lim_{θ→0}\dfrac{1−\cos θ}{θ}\).
Solución
En el primer paso, multiplicamos por el conjugado para que podamos usar una identidad trigonométrica para convertir el coseno en el numerador a un seno:
\ [\ begin {align*}\ lim_ {θ→0}\ dfrac {1−\ cos θ} {θ} &=\ displaystyle\ lim_ {θ→0}\ dfrac {1−\ cos θ} {θ} ⋅\ dfrac {1+\ cos θ} {1+\ cos θ}\\ [4pt]
&=\ lim_ {θ→0}\ dfrac {1−\ cos^2θ} {θ (1+\ cos θ)}\\ [4pt]
&=\ lim_ {θ→0}\ dfrac {\ sen ^2θ} {θ (1+\ cos θ)}\\ [4pt]
&=\ lim_ {θ→0}\ dfrac {\ sin θ } {θ} ⋅\ dfrac {\ sin θ} {1+\ cos θ}\\ [4pt]
&=\ izquierda (\ lim_ {θ→0}\ dfrac {\ sin θ} {θ}\ derecha)\ cdot\ izquierda (\ lim_ {θ→0}\ dfrac {\ sin θ} {1+\ cos θ}\ derecha)\\ [4pt]
&= 1⋅\ dfrac {0} {2} =0. \ end {alinear*}\]
Por lo tanto,
\[\lim_{θ→0}\dfrac{1−\cos θ}{θ}=0. \nonumber \]
Evaluar\(\displaystyle \lim_{θ→0}\dfrac{1−\cos θ}{\sin θ}\).
- Insinuación
-
Multiplicar numerador y denominador por\(1+\cos θ\).
- Contestar
-
0
Algunas de las fórmulas geométricas que damos por sentadas hoy en día se derivaron primero por métodos que anticipan algunos de los métodos de cálculo. El matemático griego Arquímedes (ca. 287−212; BCE) fue particularmente inventivo, utilizando polígonos inscritos dentro de círculos para aproximar el área del círculo a medida que aumentaba el número de lados del polígono. Nunca se le ocurrió la idea de un límite, pero podemos usar esta idea para ver qué podrían haber predicho sus construcciones geométricas sobre el límite.
Podemos estimar el área de un círculo calculando el área de un polígono regular inscrito. Piense en el polígono regular como formado por\(n\) triángulos. Al tomar el límite ya que el ángulo de vértice de estos triángulos va a cero, se puede obtener el área del círculo. Para ver esto, lleve a cabo los siguientes pasos:
1.Expresar la altura\(h\) y la base\(b\) del triángulo isósceles en la Figura\(\PageIndex{8}\) en términos de\(θ\) y\(r\).
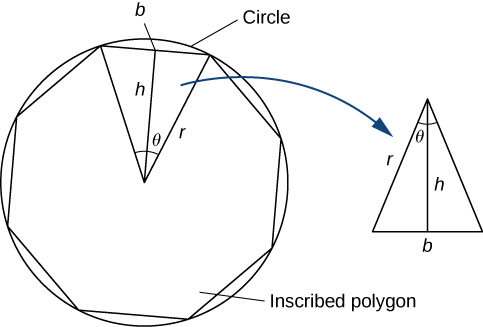
2. Usando las expresiones que obtuviste en el paso 1, expresa el área del triángulo isósceles en términos de\(θ\) y\(r\).
(Sustituto\(\frac{1}{2}\sin θ\)\(\sin\left(\frac{θ}{2}\right)\cos\left(\frac{θ}{2}\right)\) en su expresión.)
3. Si un polígono regular de\(n\) lados está inscrito en un círculo de radio\(r\), encuentre una relación entre\(θ\) y\(n\). Resuelve esto para\(n\). Ten en cuenta que hay\(2π\) radianes en un círculo. (Usar radianes, no grados.)
4. Encuentra una expresión para el área del polígono\(n\) -sided en términos de\(r\) y\(θ\).
5. Para encontrar una fórmula para el área del círculo, encuentra el límite de la expresión en el paso 4 como\(θ\) va a cero. (Pista:\(\displaystyle \lim_{θ→0}\dfrac{\sin θ}{θ}=1)\).
La técnica de estimación de áreas de regiones mediante el uso de polígonos es revisada en Introducción a la Integración.
Conceptos clave
- Las leyes de límite nos permiten evaluar límites de funciones sin tener que pasar por procesos paso a paso cada vez.
- Para polinomios y funciones racionales,\[\lim_{x→a}f(x)=f(a). \nonumber \]
- Se puede evaluar el límite de una función factorizando y cancelando, multiplicando por un conjugado, o simplificando una fracción compleja.
- El teorema squeeze permite encontrar el límite de una función si la función es siempre mayor que una función y menor que otra función con límites que se conocen.
Ecuaciones Clave
- Resultados de Límite Básico
\[\lim_{x→a}x=a \quad \quad \lim_{x→a}c=c \nonumber \]
- Límites Importantes
\[ \lim_{θ→0}\sin θ=0 \nonumber \]
\[ \lim_{θ→0}\cos θ=1 \nonumber \]
\[ \lim_{θ→0}\dfrac{\sin θ}{θ}=1 \nonumber \]
\[ \lim_{θ→0}\dfrac{1−\cos θ}{θ}=0 \nonumber \]
Glosario
- ley múltiple constante para los límites
- la ley límite\[\lim_{x→a}cf(x)=c⋅\lim_{x→a}f(x)=cL \nonumber \]
- ley de diferencia para límites
- la ley límite\[\lim_{x→a}(f(x)−g(x))=\lim_{x→a}f(x)−\lim_{x→a}g(x)=L−M\nonumber \]
- leyes de límite
- las propiedades individuales de los límites; para cada una de las leyes individuales, dejar\(f(x)\) y\(g(x)\) definirse para\(x≠a\) todo en algún intervalo abierto que contenga a; supongamos que L y M son números reales de manera que\(\lim_{x→a}f(x)=L\) y\(\lim_{x→a}g(x)=M\); dejar que c sea una constante
- ley de poder para límites
- la ley límite\[\lim_{x→a}(f(x))^n=(\lim_{x→a}f(x))^n=L^n\nonumber \] para cada entero positivo n
- ley de producto para límites
- la ley límite\[\lim_{x→a}(f(x)⋅g(x))=\lim_{x→a}f(x)⋅\lim_{x→a}g(x)=L⋅M\nonumber \]
- ley de cociente para límites
- la ley límite\(\lim_{x→a}\dfrac{f(x)}{g(x)}=\dfrac{\lim_{x→a}f(x)}{\lim_{x→a}g(x)}=\dfrac{L}{M}\) para M≠ 0
- ley raíz para límites
- la ley límite\(\lim_{x→a}\sqrt[n]{f(x)}=\sqrt[n]{\lim_{x→a}f(x)}=\sqrt[n]{L}\) para todo L si n es impar y para\(L≥0\) si n es par
- teorema de squeeze
- establece que si\(f(x)≤g(x)≤h(x)\) por\(x≠a\) todo un intervalo abierto que contiene a y\(\lim_{x→a}f(x)=L=\lim_ {x→a}h(x)\) donde L es un número real, entonces\(\lim_{x→a}g(x)=L\)
- ley de suma para límites
- La ley límite\(\lim_{x→a}(f(x)+g(x))=\lim_{x→a}f(x)+\lim_{x→a}g(x)=L+M\)



Límites de las funciones polinomiales y racionales
A estas alturas probablemente te hayas dado cuenta de que, en cada uno de los ejemplos anteriores, ha sido así\(\displaystyle \lim_{x→a}f(x)=f(a)\). Esto no siempre es cierto, pero sí se sostiene para todos los polinomios para cualquier elección de\(a\) y para todas las funciones racionales en todos los valores\(a\) para los que se define la función racional.
Límites de las funciones polinomiales y racionales
Dejar\(p(x)\) y\(q(x)\) ser funciones polinómicas. \(a\)Déjese ser un número real. Entonces,
\[\lim_{x→a}p(x)=p(a) \nonumber \]
\[\lim_{x→a}\frac{p(x)}{q(x)}=\frac{p(a)}{q(a)} \nonumber \]
cuando\(q(a)≠0\).
Para ver que este teorema sostiene, considera el polinomio
\[p(x)=c_nx^n+c_{n−1}x^{n−1}+⋯+c_1x+c_0. \nonumber \]
Al aplicar las leyes de suma, múltiplo constante y poder, terminamos con
\[ \begin{align*} \lim_{x→a}p(x) &= \lim_{x→a}(c_nx^n+c_{n−1}x^{n−1}+⋯+c_1x+c_0) \\[4pt] &= c_n\left(\lim_{x→a}x\right)^n+c_{n−1}\left(\lim_{x→a}x\right)^{n−1}+⋯+c_1\left(\lim_{x→a}x\right)+\lim_{x→a}c_0 \\[4pt] &= c_na^n+c_{n−1}a^{n−1}+⋯+c_1a+c_0 \\[4pt] &= p(a) \end{align*}\]
Ahora se deduce de la ley del cociente que si\(p(x)\) y\(q(x)\) son polinomios para los cuales\(q(a)≠0\),
entonces
\[\lim_{x→a}\frac{p(x)}{q(x)}=\frac{p(a)}{q(a)}. \nonumber \]
Ejemplo\(\PageIndex{3}\): Evaluating a Limit of a Rational Function
Evaluar el\(\displaystyle \lim_{x→3}\frac{2x^2−3x+1}{5x+4}\).
Solución
Dado que 3 está en el dominio de la función racional\(f(x)=\displaystyle \frac{2x^2−3x+1}{5x+4}\), podemos calcular el límite sustituyendo 3 por\(x\) en la función. Por lo tanto,
\[\lim_{x→3}\frac{2x^2−3x+1}{5x+4}=\frac{10}{19}. \nonumber \]
Ejercicio\(\PageIndex{3}\)
Evaluar\(\displaystyle \lim_{x→−2}(3x^3−2x+7)\).
Usar LÍMITES DE FUNCIONES POLINOMIALES Y RACIALES como referencia
−13