5.2: La Integral Definitiva

Última actualización
Guardar como PDF

Page ID: 111789

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Empezamos con un problema fácil. Un objeto viaja en línea recta a una velocidad constante de 5 pies/s durante 10 segundos. ¿Qué tan lejos de su punto de partida está el objeto?

Abordamos este problema con la familiar ecuación de “Distance$=$ Rate$\times$ Time”. En este caso, Distancia = 5ft/s$\times$ 10s$=$ 50 pies.

Es interesante señalar que esta solución de 50 pies se puede representar gráficamente. Considere la Figura$\PageIndex{1}$, donde la velocidad constante de 5ft/s se grafica en los ejes. Sombrear el área debajo de la línea de$t=0$ a$t=10$ da un rectángulo con un área de 50 unidades cuadradas; cuando se consideran las unidades de los ejes, podemos decir que esta área representa 50 pies.

$alt$

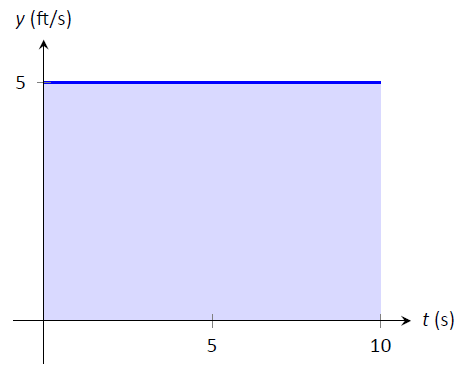
Figura$\PageIndex{1}$: El área bajo una función de velocidad constante corresponde a la distancia recorrida.

Ahora considere una situación un poco más difícil (y no particularmente realista): un objeto viaja en línea recta con una velocidad constante de 5 pies/s durante 10 segundos, luego invierte el rumbo instantáneamente a una velocidad de 2 pies/s durante 4 segundos. (Dado que el objeto está viajando en sentido contrario al invertir rumbo, decimos que la velocidad es constante$-2$ ft/s.) A qué distancia del punto de partida está el objeto — ¿cuál es su desplazamiento?

Aquí usamos “Tiempo de$=$ tasa de distancia$_1$ +$_1$$\times$$_2$$\times$ Tiempo de tasa”$_2$, que es

\[\text{Distance } \ = 5\cdot10 + (-2)\cdot 4 = 42\text{ ft.}\]

De ahí que el objeto se encuentre a 42 pies de su ubicación inicial.

De nuevo podemos representar gráficamente esta situación. En la Figura$\PageIndex{3}$ tenemos las velocidades graficadas como líneas rectas sobre$[0,10]$ y$[10,14]$, respectivamente. El desplazamiento del objeto es

\[\text{"Area above the $t$--axis} \quad - \quad \text{Area below the $t$-axis,} \]

que es fácil de calcular como$50-8=42$ pies.

$alt$

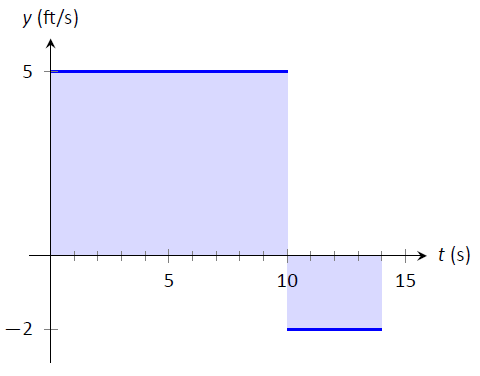
Figura$\PageIndex{2}$: El desplazamiento total es el área por encima del$t$ eje —menos el área por debajo del$t$ eje —.

Consideremos ahora un problema más difícil.

Ejemplo$\PageIndex{1}$: Finding position using velocity

La velocidad de un objeto que se mueve recto arriba/abajo bajo la aceleración de la gravedad se da como$v(t) = -32t+48$, donde el tiempo$t$ se da en segundos y la velocidad es en pies/s. cuando$t=0$, el objeto tenía una altura de 0 pies.

¿Cuál fue la velocidad inicial del objeto?
¿Cuál era la altura máxima del objeto?
¿Cuál era la altura del objeto en el momento$t=2$?

Solución

Es sencillo encontrar la velocidad inicial; a la vez$t=0$,$v(0) =-32\cdot 0+48 = 48$ pies/s.

Para responder preguntas sobre la altura del objeto, necesitamos encontrar la función de posición del objeto$s(t)$. Se trata de un problema de valor inicial, que estudiamos en la sección anterior. Se nos dice que la altura inicial es 0, es decir,$s(0) = 0$. Sabemos$s'(t) = v(t) = -32t+48$. Para encontrar$s$, encontramos la integral indefinida de$v(t)$:

\[\int v(t)\ dt = \int (-32t+48)\ dt = -16t^2+48t+C = s(t).\]

Ya que$s(0) = 0$, concluimos que$C=0$ y$s(t) = -16t^2+48t$.

Para encontrar la altura máxima del objeto, necesitamos encontrar la máxima de$s$. Recordando nuestro trabajo encontrando valores extremos, encontramos los puntos críticos de$s$ al establecer su derivada igual a 0 y resolviendo para$t$:

\[s'(t) = -32t+48 = 0 \quad \Rightarrow \quad t=48/32 = 1.5\text{s}.\]

(¡Observe cómo acabamos encontrando cuando la velocidad era de 0 pies/s!) La primera prueba derivada muestra que este es un máximo, por lo que la altura máxima del objeto se encuentra en

\[s(1.5) = -16(1.5)^2+48(1.5)=36\text{ft}.\]

La altura en el momento ahora$t=2$ es fácil de calcular: es$s(2) = 32$ ft.

Si bien hemos respondido a las tres preguntas, volvamos a verlas gráficamente, utilizando los conceptos de área que exploramos anteriormente.

La figura$\PageIndex{3}$ muestra una gráfica de$v(t)$ sobre ejes de$t=0$ a$t=3$. De nuevo es sencillo de encontrar$v(0)$. ¿Cómo podemos usar la gráfica para encontrar la altura máxima del objeto?

$alt$

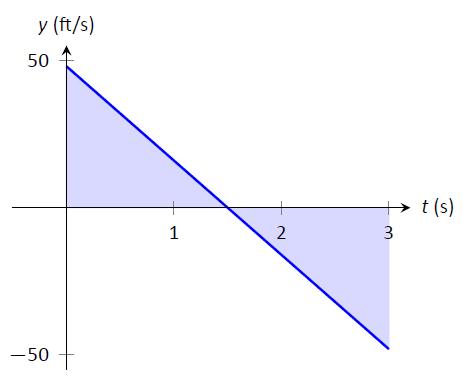
Figura$\PageIndex{3}$: Una gráfica de$v(t)=-32t+48$; las áreas sombreadas ayudan a determinar el desplazamiento.

Recordemos cómo en nuestro trabajo anterior se encontró el desplazamiento del objeto (en este caso, su altura) como el área bajo la curva de velocidad, como sombreado en la figura. Además, el área entre la curva y el$t$ eje —que está por debajo del$t$ eje —se cuenta como área “negativa”. Es decir, representa el objeto volviendo hacia su posición inicial. Entonces, para encontrar la distancia máxima desde el punto de partida —la altura máxima— encontramos el área debajo de la línea de velocidad que está por encima del$t$ eje —es decir, de$t=0$ a$t=1.5$. Esta región es un triángulo; su área es

\[\text{Area } = \frac12\text{Base} \times \text{Height} =\frac12\times 1.5\text{s}\times 48\text{ft/s} = 36\text{ft},\]

que coincide con nuestro cálculo anterior de la altura máxima.

Finalmente, encontramos el área total firmada bajo la función de velocidad de$t=0$$t=2$ a para encontrar la$s(2)$, la altura a$t=2$, que es un desplazamiento, la distancia desde la posición actual a la posición inicial. Es decir,

\[ \text{Displacement} = \text{Area above the $t-$axis} - \text{Area below $t$-axis.}\]

Las regiones son triángulos, y encontramos

$$\ text {Desplazamiento} =\ frac12 (1.5\ texto {s}) (48\ texto {ft/s}) -\ frac12 (.5\ texto {s}) (16\ texto {ft/s}) = 32\ texto {ft}.\]

Esto también coincide con nuestro cálculo anterior de la altura a$t=2$.

Observe cómo respondimos cada pregunta en este ejemplo de dos maneras. Nuestro primer método fue manipular ecuaciones usando nuestra comprensión de antiderivados y derivados. Nuestro segundo método fue geométrico: respondimos preguntas mirando una gráfica y encontrando las áreas de ciertas regiones de esta gráfica.

El ejemplo anterior no prueba una relación entre el área bajo una función de velocidad y el desplazamiento, pero sí implica que existe una relación. La sección 5.4 establecerá completamente el hecho de que el área bajo una función de velocidad es el desplazamiento.

Dada una gráfica de una función$y=f(x)$, encontraremos que hay un gran uso en el cálculo del área entre la curva$y=f(x)$ y el$x$ eje -eje. Debido a esto, necesitamos definir algunos términos.

Definición$\PageIndex{1}$: The Definite Integral, Total Signed Area

Dejar$y=f(x)$ ser definido en un intervalo cerrado$[a,b]$. El área total firmada de$x=a$ a$x=b$ menos$f$ es:

\[(\text{area under $f$ and above the $x$-axis on $[a,b]$)}. - (\text{area above $f$ and under the $x$-axis on $[a,b]$}). \]

La integral definitiva de$f$ on$[a,b]$ es el área total firmada de$f$ on$[a,b]$, denotada

\[\int_a^b f(x)\ dx,\]

Ahí$a$ y$b$ están los límites de la integración.

Por nuestra definición, la integral definida da el “área firmada bajo”$f$. Solemos caer la palabra “firmado” cuando hablamos de la integral definida, y simplemente decimos que la integral definida da “el área bajo$f$\”, o, más comúnmente, “el área bajo la curva”.

En el apartado anterior se introdujo la integral indefinida, la cual se relacionó con los antiderivados. Ahora hemos definido la integral definida, que se relaciona con áreas bajo una función. Los dos están muy relacionados, como veremos cuando aprendamos el Teorema Fundamental del Cálculo en la Sección 5.4. Recordemos que antes dijimos que el símbolo$\int$ "" era una “S alargada” que representaba encontrar una “suma”. En el contexto de la integral definida, esta notación tiene un poco más de sentido, ya que estamos sumando áreas bajo la función$f$.

Practicamos usando esta notación.

Ejemplo$\PageIndex{2}$: Evaluating definite integrals

Considera la función$f$ dada en la Figura$\PageIndex{4}$.

$alt$

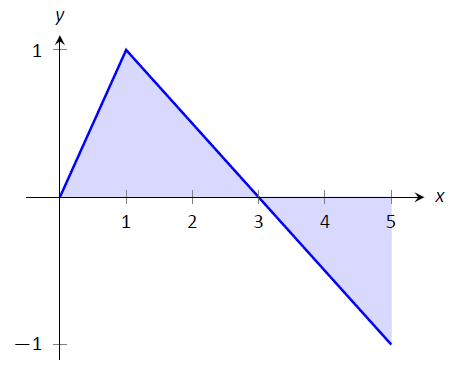
Figura$\PageIndex{4}$: Un gráfico de$f(x)$ en Ejemplo$2$

Encuentra:

$\int_0^3 f(x)\ dx$
$\int_3^5 f(x)\ dx$
$\int_0^5 f(x)\ dx$
$\int_0^3 5f(x)\ dx$
$\int_1^1 f(x) \ dx$

Solución

$\int_0^3 f(x) dx$es el área debajo$f$ del intervalo$[0,3]$. Esta región es un triángulo, por lo que el área es$\int_0^3 f(x) dx=\frac12(3)(1) = 1.5$.
$\int_3^5 f(x) dx$representa el área del triángulo que se encuentra bajo el$x$ eje —en$[3,5]$. El área es$\frac12(2)(1) = 1$; ya que se encuentra bajo el$x$ eje —se trata de “área negativa”. Por lo tanto$\int_3^5 f(x)\ dx = -1$.
$\int_0^5f(x) dx$es el área total firmada bajo$f$ on$[0,5]$. Esto es$1.5 + (-1) = 0.5$.
$ \int_0^35f(x) dx$es el área debajo$5f$ de$[0,3]$. Esto se esboza en la Figura$\PageIndex{5}$. Nuevamente, la región es un triángulo, con una altura 5 veces mayor que la altura del triángulo original. Así el área es$\int_0^35f(x)\ dx = 15/2 = 7.5.$

$alt$

Figura$\PageIndex{5}$: Una gráfica de$5f$ en Ejemplo$\PageIndex{2}$. (Sí, se ve igual que la gráfica de$f$ en Figura$\PageIndex{4}$, solo con una$y$ escala diferente.)

$\int_1^1f(x) dx$es el área debajo$f$ en el “intervalo”$[1,1]$. Esto describe un segmento de línea, no una región; no tiene ancho. Por lo tanto el área es 0.

Este ejemplo ilustra algunas de las propiedades de la integral definida, dadas aquí.

Teorema$\PageIndex{2}$: Properties of the Definite Integral

Let$f$ y$g$ ser definido en un intervalo cerrado$I$ que contiene los valores$a$,$b$ y$c$, y let$k$ ser una constante. Se mantienen los siguientes:

$\int_a^a f(x) dx = 0$
$\int_a^b f(x) dx + \int_b^c f(x) dx = \int_a^cf(x) dx$
$\int_a^bf(x) dx = -\int_b^a f(x) dx$
$\int_a^b\big(f(x)\pm g(x)\big) dx = \int_a^bf(x)\ dx \pm \int_a^bg(x) dx$
$\int_a^bk\cdot f(x) dx = k\cdot\int_a^bf(x) dx$

Damos una breve justificación del Teorema$\PageIndex{2}$ aquí.

Como se demuestra en Ejemplo$\PageIndex{2}$, no hay “área bajo la curva” cuando la región no tiene ancho; de ahí que esta integral definida sea 0.
Esto establece que la superficie total es la suma de las áreas de las subregiones. Se considera fácilmente cuando dejamos$a<b<c$. Podemos romper el intervalo$[a,c]$ en dos subintervalos,$[a,b]$ y$[b,c]$. El área total sobre$[a,c]$ es el área sobre$[a,b]$ más el área sobre$[b,c]$.
Es importante señalar que esto sigue siendo cierto aunque no$a<b<c$ sea cierto. Esto lo discutimos en el siguiente punto.
Esta propiedad se puede ver simplemente como una convención para hacer que otras propiedades funcionen bien. (Posteriormente veremos como esta propiedad tiene una justificación propia, no necesariamente en apoyo de otras propiedades.) Supongamos$b<a<c$. La discusión desde el punto anterior justifica claramente\[\int_b^a f(x) dx + \int_a^c f(x)\ dx = \int_b^c f(x) dx.\]
Sin embargo, seguimos alegando que, como se dijo originalmente,\[\int_a^b f(x)\ dx + \int_b^c f(x)\ dx = \int_a^c f(x)\ dx.\]
¿Cómo$\PageIndex{12}$ se relacionan las ecuaciones$\PageIndex{11}$ y? Empezar con Ecuación$\PageIndex{11}$:\[\begin{align} \int_b^a f(x) dx + \int_a^c f(x) dx &= \int_b^c f(x) dx\\ \int_a^c f(x)\ dx &= -\int_b^a f(x) dx + \int_b^c f(x) dx \end{align}\]
Propiedad$(3)$ justifica cambiar el signo y cambiar los límites de integración en el$-\int_b^a f(x) dx$ término; cuando esto se hace, Ecuaciones$\PageIndex{11}$ y$\PageIndex{12}$ son equivalentes.
La conclusión es la siguiente: al adoptar la convención de Bienes (3), Propiedad (2) se mantiene sin importar el orden de$a$,$b$ y$c$. Nuevamente, en la siguiente sección veremos otra justificación para esta propiedad.
,5. Cada uno de estos puede ser poco intuitivo. La propiedad (5) establece que cuando se escala una función por, por ejemplo, 7, el área de la región cerrada también se escala por un factor de 7. Ambas Propiedades (4) y (5) se pueden probar usando geometría. Los detalles no son complicados pero no se discuten aquí.

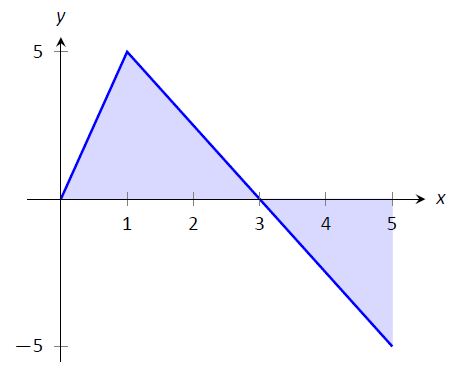
Ejemplo$\PageIndex{3}$: Evaluating definite integrals using Theorem $\PageIndex{2}$.

Considera la gráfica de una función que$f(x)$ se muestra en la Figura$\PageIndex{6}$.

$alt$

Figura$\PageIndex{6}$: Una gráfica de una función en Ejemplo$\PageIndex{3}$

Responde lo siguiente:

¿Qué valor es mayor:$\int_a^b f(x) dx$ o$ \int_b^c f(x) dx$?
¿Es$\int_a^c f(x) dx$ mayor o menor que 0?
¿Qué valor es mayor:$\int_a^b f(x) dx$ o$\int_c^b f(x) dx$?

Solución

$\int_a^b f(x) dx$tiene un valor positivo (ya que el área está por encima del$x$ eje —) mientras que$\int_b^c f(x) dx$ tiene un valor negativo. De ahí$\int_a^b f(x) dx$ que sea más grande.
$\int_a^c f(x) dx$es el área total firmada bajo$f$ entre$x=a$ y$x=c$. Dado que la región debajo del$x$ eje —parece ser mayor que la región anterior, concluimos que la integral definida tiene un valor menor que 0.
Observe cómo la segunda integral tiene los límites “invertidos”. Por lo tanto,$\int_c^b f(x) dx$ representa un número positivo, mayor que el área descrita por la primera integral definida. De ahí$\int_c^b f(x) dx$ que sea mayor.

La definición de área de la integral definida nos permite usar geometría computar la integral definida de algunas funciones simples.

Ejemplo$\PageIndex{4}$: Evaluating definite integrals using geometry

Evalúe las siguientes integrales definidas:

\[1. \ \int_{-2}^5 (2x-4)\ dx \qquad 2.\ \int_{-3}^3 \sqrt{9-x^2}\ dx.\]

Solución

$alt$ $alt$

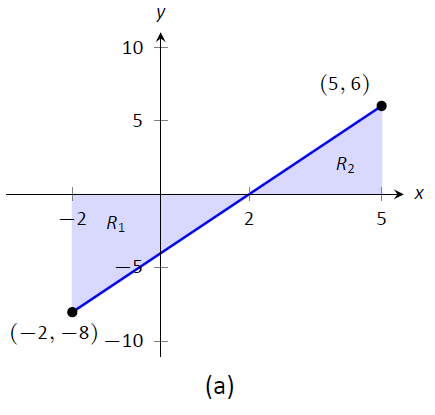
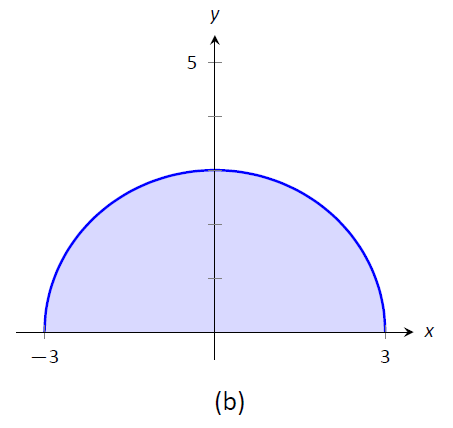
Figura$\PageIndex{7}$: Un gráfico de$f(x) = 2x-4$ en (a) y$f(x) = \sqrt{9-x^2}$ en (b), del Ejemplo$\PageIndex{4}$

Es útil esbozar la función en el integrando, como se muestra en la Figura$\PageIndex{7a}$. Vemos que necesitamos computar las áreas de dos regiones, que hemos etiquetado$R_1$ y$R_2$. Ambos son triángulos, por lo que el cálculo del área es sencillo: $$R_1:\ frac12 (4) (8) = 16\ qquad R_2:\ frac12 (3) 6 = 9.$$ La región$R_1$ se encuentra bajo el$x$ eje —, de ahí que se cuente como área negativa (podemos pensar en la altura del triángulo como "$-8$“), entonces $$\ int_ {-2} ^5 (2x-4)\ dx = +9 = -7. $$
Reconocer que el integrando de esta integral definida describe un semicírculo, como se esboza en la Figura$\PageIndex{7b}$, con radio 3. Así el área es:

$$\ int_ {-3} ^3\ sqrt {9-x^2}\ dx =\ frac12\ pi r^2 =\ frac 92\ pi.\]

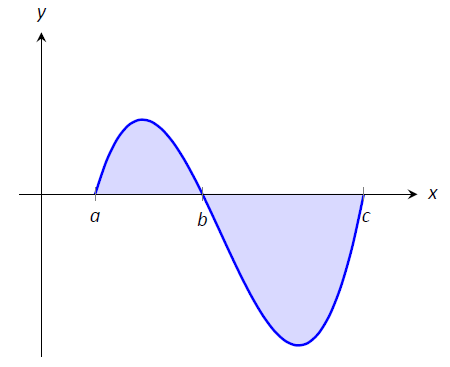
Ejemplo$\PageIndex{5}$: Understanding motion given velocity

Considera la gráfica de una función de velocidad de un objeto que se mueve en línea recta, dada en la Figura$\PageIndex{8}$, donde los números en las regiones dadas dan el área de esa región. Supongamos que la integral definida de una función de velocidad da desplazamiento. Encuentra la velocidad máxima del objeto y su desplazamiento máximo desde su posición inicial.

Solución

$alt$

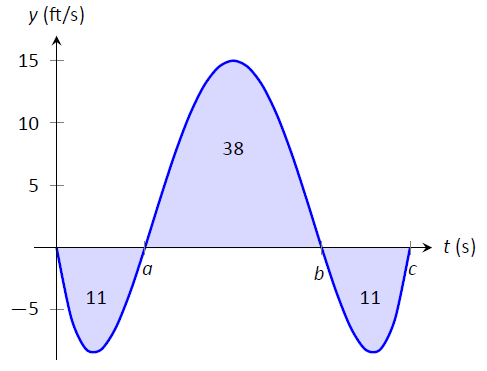
Figura$\PageIndex{8}$: Un gráfico de una velocidad en el Ejemplo$\PageIndex{5}$.

Dado que la gráfica da velocidad, encontrar la velocidad máxima es simple: parece ser de 15 pies/s.

En el momento$t=0$, el desplazamiento es 0; el objeto está en su posición inicial. En su momento$t=a$, el objeto se ha movido hacia atrás 11 pies. Entre tiempos$t=a$ y$t=b$, el objeto se mueve hacia adelante 38 pies, llevándolo a una posición 27 pies adelante de su posición inicial. De$t=b$$t=c$ al objeto se está moviendo de nuevo hacia atrás, de ahí que su desplazamiento máximo sea de 27 pies desde su posición inicial.

En nuestros ejemplos, o bien hemos encontrado las áreas de regiones que tienen bonitas formas geométricas (como rectángulos, triángulos y círculos) o las áreas que nos fueron dadas. Considera Figura$\PageIndex{9}$, donde una región de abajo$y=x^2$ está sombreada. ¿Cuál es su área? La función$y=x^2$ es relativamente simple, sin embargo la forma que define tiene un área que no es sencilla de encontrar geométricamente.

$alt$

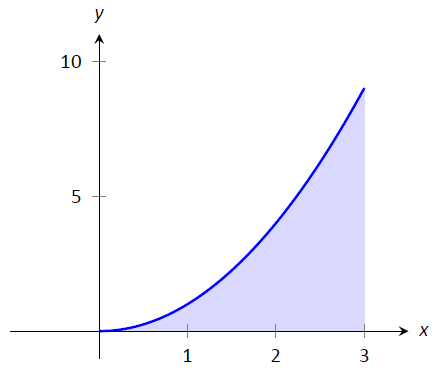
Figura$\PageIndex{9}$: ¿Cuál es el área de abajo$y=x^2$ en$[0,3]$? La región no es una forma geométrica habitual.

En la siguiente sección exploraremos cómo encontrar las zonas de dichas regiones.