5.2: La Integral Definitiva
- Page ID
- 116211
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Afirmar la definición de la integral definida.
- Explicar los términos integrando, límites de integración y variable de integración.
- Explique cuándo una función es integrable.
- Describir la relación entre la integral definida y el área neta.
- Usa la geometría y las propiedades de integrales definidas para evaluarlas.
- Calcular el valor promedio de una función.
En la sección anterior definimos el área bajo una curva en términos de sumas de Riemann:
\[A=\lim_{n→∞}\sum_{i=1}^nf(x^∗_i)Δx. \nonumber \]
Sin embargo, esta definición vino con restricciones. Se requería\(f(x)\) ser continuo y no negativo. Desafortunadamente, los problemas del mundo real no siempre cumplen con estas restricciones. En esta sección, analizamos cómo aplicar el concepto del área bajo la curva a un conjunto más amplio de funciones mediante el uso de la integral definida.
Definición y Notación
La integral definida generaliza el concepto del área bajo una curva. Elevamos los requisitos que\(f(x)\) sean continuos y no negativos, y definimos la integral definida de la siguiente manera.
Si\(f(x)\) es una función definida en un intervalo,\([a,b],\) la integral definida de\(f\) from\(a\) to\(b\) viene dada por
\[∫^b_af(x)\,dx=\lim_{n→∞} \sum_{i=1}^nf(x^∗_i)Δx, \nonumber \]
siempre que exista el límite. Si existe este límite,\(f(x)\) se dice que la función es integrable en\([a,b]\), o es una función integrable.
El símbolo integral en la definición anterior debería parecer familiar. Hemos visto una notación similar en el capítulo de Aplicaciones de Derivados, donde se utilizó el símbolo integral indefinido (sin el\(a\) y\(b\) arriba y abajo) para representar una antiderivada. Aunque la notación para integrales indefinidas puede parecer similar a la notación para una integral definida, no son lo mismo. Una integral definida es un número. Una integral indefinida es una familia de funciones. Posteriormente en este capítulo examinamos cómo se relacionan estos conceptos. Sin embargo, siempre se debe prestar mucha atención a la notación para que sepamos si estamos trabajando con una integral definida o una integral indefinida.
La notación integral se remonta a finales del siglo XVII y es una de las aportaciones de Gottfried Wilhelm Leibniz, quien a menudo es considerado como el codescubridor del cálculo, junto con Isaac Newton. El símbolo de integración\(∫\) es un alargado\(S\), sugiriendo sigma o suma. En una integral definida, por encima y por debajo del símbolo de suma están los límites del intervalo,\([a,b].\) Los números\(a\) y\(b\) son\(x\) -valores y se denominan los límites de integración; específicamente,\(a\) es el límite inferior y\(b\) es el límite superior. Para aclarar, estamos utilizando la palabra límite de dos maneras diferentes en el contexto de la integral definida. Primero, hablamos del límite de una suma como\(n→∞.\) Segundo, los límites de la región se llaman los límites de la integración.
Llamamos a la función\(f(x)\) el integrando, y el\(dx\) indica que\(f(x)\) es una función con respecto a\(x\), llamada la variable de integración. Tenga en cuenta que, al igual que el índice en una suma, la variable de integración es una variable ficticio, y no tiene impacto en el cálculo de la integral. Podríamos usar cualquier variable que nos guste como la variable de integración:
\[∫^b_af(x)\,dx=∫^b_af(t)\,dt=∫^b_af(u)\,du \nonumber \]
Anteriormente, discutimos el hecho de que si\(f(x)\) es continuo en\([a,b],\) entonces el límite\(\displaystyle \lim_{n→∞}\sum_{i=1}^nf(x^∗_i)Δx\) existe y es único. Esto lleva al siguiente teorema, que declaramos sin pruebas.
Si\(f(x)\) es continuo encendido\([a,b]\), entonces\(f\) es integrable en\([a,b].\)
Las funciones que no son continuas\([a,b]\) pueden seguir siendo integrables, dependiendo de la naturaleza de las discontinuidades. Por ejemplo, las funciones con un número finito de discontinuidades de salto o discontinuidades removibles en un intervalo cerrado son integrables.
También vale la pena señalar aquí que hemos conservado el uso de una partición regular en las sumas de Riemann. Esta restricción no es estrictamente necesaria. Cualquier partición se puede utilizar para formar una suma de Riemann. Sin embargo, si se usa una partición no regular para definir la integral definida, no es suficiente tomar el límite ya que el número de subintervalos va al infinito. En cambio, debemos tomar el límite ya que el ancho del subintervalo más grande va a cero. Esto introduce una notación un poco más compleja en nuestros límites y hace que los cálculos sean más difíciles sin realmente obtener mucha información adicional, por lo que nos quedamos con particiones regulares para las sumas de Riemann.
Utilice la definición de la integral definida para evaluar\(\displaystyle ∫^2_0x^2\,dx.\) Utilice una aproximación de punto final derecho para generar la suma de Riemann.
Solución
Primero queremos establecer una suma de Riemann. En base a los límites de la integración, tenemos\(a=0\) y\(b=2\). Para\(i=0,1,2,…,n\), deja\(P={x_i}\) ser una partición regular de\([0,2].\) Entonces
\[Δx=\dfrac{b−a}{n}=\dfrac{2}{n}. \nonumber \]
Ya que estamos usando una aproximación de punto final derecho para generar sumas de Riemann, para cada una\(i\), necesitamos calcular el valor de la función en el punto final derecho del intervalo\([x_{i−1},x_i].\) El punto final derecho del intervalo es\(x_i\), y ya que\(P\) es una partición regular,
\[x_i=x_0+iΔx=0+i\left[\dfrac{2}{n}\right]=\dfrac{2i}{n}.\nonumber \]
Por lo tanto, el valor de la función en el punto final derecho del intervalo es
\[f(x_i)=x^2_i=\left(\dfrac{2i}{n}\right)^2=\dfrac{4i^2}{n^2}.\nonumber \]
Entonces la suma de Riemann toma la forma
\[\sum_{i=1}^nf(x_i)Δx=\sum_{i=1}^n\left(\dfrac{4i^2}{n^2}\right)\dfrac{2}{n}=\sum_{i=1}^n\dfrac{8i^2}{n^3}=\dfrac{8}{n^3}\sum_{i=1}^ni^2.\nonumber \]
Usando la fórmula de suma para\(\displaystyle \sum_{i=1}^ni^2\), tenemos
\[\begin{align*} \sum_{i=1}^nf(x_i)Δx &=\dfrac{8}{n^3}\sum_{i=1}^ni^2 \\[4pt] &=\dfrac{8}{n^3}\left[\dfrac{n(n+1)(2n+1)}{6}\right] \\[4pt] &=\dfrac{8}{n^3}\left[\dfrac{2n^3+3n^2+n}{6}\right] \\[4pt] &=\dfrac{16n^3+24n^2+n}{6n^3} \\[4pt] &=\dfrac{8}{3}+\dfrac{4}{n}+\dfrac{1}{6n^2}. \end{align*}\]
Ahora bien, para calcular la integral definida, necesitamos tomar el límite como\(n→∞\). Obtenemos
\ [\ begin {align*} ^2_0x^2dx &=\ lim_ {n→∞}\ suma_ {i=1} ^nf (x_i) Δx\\ [4pt]
&=\ lim_ {n→∞}\ izquierda (\ dfrac {8} {3} +\ dfrac {4} {n} +\ dfrac {1} {6n^2}\ derecha)\\ [4pt]
&=\ lim_ {n→∞}\ izquierda (\ dfrac {8} {3}\ derecha) +\ lim_ {n→∞}\ izquierda (\ dfrac {4} {n}\ derecha) +\ lim_ {n→∞}\ izquierda (\ dfrac {1} {6n^2}\ derecha)\\ [4pt]
&=\ dfrac {8} {3} +0+0=\ dfrac {8} {3}. \ end {alinear*}\]
Utilizar la definición de la integral definida para evaluar\(\displaystyle ∫^3_0(2x−1)\,dx\).
Utilice una aproximación de punto final derecho para generar la suma de Riemann.
- Pista
-
Usa la estrategia de resolución de Example\(\PageIndex{1}\).
- Contestar
-
6
Evaluación de Integrales Definidas
Evaluar integrales definidas de esta manera puede ser bastante tedioso debido a la complejidad de los cálculos. Posteriormente en este capítulo desarrollamos técnicas para evaluar integrales definidas sin tomar límites de sumas de Riemann. Sin embargo, por ahora, podemos confiar en el hecho de que las integrales definidas representan el área bajo la curva, y podemos evaluar integrales definidas usando fórmulas geométricas para calcular esa área. Hacemos esto para confirmar que las integrales definidas sí representan, de hecho, áreas, para luego discutir qué hacer en el caso de una curva de una función cayendo por debajo del\(x\) eje -eje.
Utilice la fórmula para el área de un círculo para evaluar\(\displaystyle ∫^6_3\sqrt{9−(x−3)^2}\,dx\).
Solución
La función describe un semicírculo con radio 3. Para encontrar
\[∫^6_3\sqrt{9−(x−3)^2}\,dx \nonumber \]
queremos encontrar el área bajo la curva sobre el intervalo\([3,6].\) La fórmula para el área de un círculo es\(A=πr^2\). El área de un semicírculo es solo la mitad del área de un círculo, o\(A=\dfrac{1}{2}πr^2\). El área sombreada en la Figura\(\PageIndex{1}\) cubre la mitad del semicírculo, o\(A=\dfrac{1}{4}πr^2\). Así,
\[∫^6_3\sqrt{9−(x−3)^2}\,dx=\dfrac{1}{4}π(3)^2=\dfrac{9}{4}π≈7.069. \nonumber \]
![Una gráfica de un semicírculo en el cuadrante uno sobre el intervalo [0,6] con centro en (3,0). El área bajo la curva sobre el intervalo [3,6] está sombreada en azul.](https://math.libretexts.org/@api/deki/files/12421/5.2.1.png)
Utilice la fórmula para el área de un trapecio para evaluar\(\displaystyle ∫^4_2(2x+3)\,dx\).
- Pista
-
Grafique la función\(f(x)\) y calcule el área debajo de la función en el intervalo\([2,4].\)
- Contestar
-
18 unidades cuadradas
Área y la Integral Definida
Cuando definimos la integral definida, levantamos el requisito de que no\(f(x)\) sea negativo. Pero, ¿cómo interpretamos “el área bajo la curva” cuando\(f(x)\) es negativo?
Área Neto Firmada
Volvamos a la suma de Riemann. Consideremos, por ejemplo, la función\(f(x)=2−2x^2\) (mostrada en la Figura\(\PageIndex{2}\)) en el intervalo\([0,2]\). Use\(n=8\) y elija {\(x^∗_i\)} como el punto final izquierdo de cada intervalo. Construye un rectángulo en cada subintervalo de alto\(f(x^∗_i)\) y ancho\(Δx\). Cuando\(f(x^∗_i)\) es positivo, el producto\(f(x^∗_i)Δx\) representa el área del rectángulo, como antes. Cuando\(f(x^∗_i)\) es negativo, sin embargo, el producto\(f(x^∗_i)Δx\) representa el negativo del área del rectángulo. La suma de Riemann se convierte entonces
\[\sum_{i=1}^8f(x^∗_i)Δx= (\text{Area of rectangles above the }x\text{-axis})−(\text{Area of rectangles below the }x\text{-axis}) \nonumber \]
![Una gráfica de una parábola de apertura hacia abajo sobre [-1, 2] con vértice en (0,2) y x-intercepta en (-1,0) y (1,0). Ocho rectángulos se dibujan uniformemente sobre [0,2] con alturas determinadas por el valor de la función en los extremos izquierdos de cada uno.](https://math.libretexts.org/@api/deki/files/2586/CNX_Calc_Figure_05_02_003.jpeg)
Tomando el límite a medida que\(n→∞,\) la suma de Riemann se acerca al área entre la curva por encima del\(x\) eje -y el\(x\) eje -eje, menos el área entre la curva por debajo del\(x\) eje -eje y el\(x\) -eje, como se muestra en la Figura\(\PageIndex{3}\). Entonces,
\[\int^2_0f(x)\,dx=\lim_{n→∞}\sum_{i=1}^nf(c_i)Δx=A_1−A_2. \nonumber \]
La cantidad\(A_1−A_2\) se denomina área neta firmada.
![Una gráfica de una parábola de apertura hacia abajo sobre [-2, 2] con vértice en (0,2) y x-intercepta en (-1,0) y (1,0). El área en el cuadrante uno bajo la curva está sombreada en azul y etiquetada como A1. El área en el cuadrante cuatro por encima de la curva y a la izquierda de x=2 está sombreada en azul y etiquetada como A2.](https://math.libretexts.org/@api/deki/files/2587/CNX_Calc_Figure_05_02_002.jpeg)
Observe que el área neta firmada puede ser positiva, negativa o cero. Si el área por encima del\(x\) eje -es mayor, el área neta firmada es positiva. Si el área por debajo del\(x\) eje -es mayor, el área neta firmada es negativa. Si las áreas por encima y por debajo del\(x\) eje -son iguales, el área neta firmada es cero.
Encuentra el área con signo neto entre la curva de la función\(f(x)=2x\) y el\(x\) eje -sobre el intervalo\([−3,3].\)
Solución
La función produce una línea recta que forma dos triángulos: uno de\(x=−3\) a\(x=0\) y el otro de\(x=0\) a\(x=3\) (Figura\(\PageIndex{4}\)). Usando la fórmula geométrica para el área de un triángulo,\(A=\dfrac{1}{2}bh\), el área del triángulo\(A_1\), por encima del eje, es
\(A_1=\dfrac{1}{2}3(6)=9\),
donde\(3\) esta la base y\(2(3)=6\) es la altura. El área del triángulo\(A_2\), debajo del eje, es
\(A_2=\dfrac{1}{2}(3)(6)=9,\)
donde\(3\) esta la base y\(6\) es la altura. Así, la superficie neta es
\(\displaystyle ∫^3_{−3}2x\,dx=A_1−A_2=9−9=0.\)
![Una gráfica de una línea creciente sobre [-6, 6] pasando por el origen y (-3, -6) y (3,6). El área debajo de la línea en el cuadrante uno sobre [0,3] está sombreada en azul y etiquetada como A1, y el área por encima de la línea en el cuadrante tres sobre [-3,0] está sombreada de azul y etiquetada como A2.](https://math.libretexts.org/@api/deki/files/12422/5.2.2.png)
Análisis
Si\(A_1\) es el área por encima del\(x\) eje y\(A_2\) es el área por debajo del\(x\) eje, entonces el área neta es\(A_1−A_2\). Dado que las áreas de los dos triángulos son iguales, el área neta es cero.
Encuentra el área neta firmada de\(f(x)=x−2\) sobre el intervalo\([0,6]\), ilustrada en la siguiente imagen.
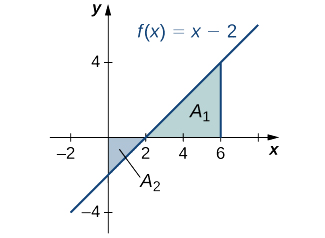
- Pista
-
Utilice el método de resolución descrito en Ejemplo\(\PageIndex{3}\).
- Contestar
-
6
Área Total
Una aplicación de la integral definida es encontrar desplazamiento cuando se le da una función de velocidad. Si\(v(t)\) representa la velocidad de un objeto en función del tiempo, entonces el área bajo la curva nos dice qué tan lejos está el objeto de su posición original. Esta es una aplicación muy importante de la integral definida, y la examinamos con más detalle más adelante en el capítulo. Por ahora, solo vamos a ver algunos conceptos básicos para tener una idea de cómo funciona esto estudiando velocidades constantes.
Cuando la velocidad es una constante, el área bajo la curva es solo velocidad por tiempo. Esta idea ya es muy familiar. Si un automóvil se aleja de su posición inicial en línea recta a una velocidad de\(70\) mph durante\(2\) horas, entonces está a\(140\) millas de su posición original (Figura\(\PageIndex{5}\)). Usando notación integral, tenemos
\[∫^2_0 70\,dt=140 \,\text{miles}. \nonumber \]
![Una gráfica en el cuadrante 1 con el eje x etiquetado como t (horas) y el eje y etiquetado como v (mi/hr). El área bajo la línea v (t) = 75 está sombreada en azul sobre [0,2].](https://math.libretexts.org/@api/deki/files/2590/CNX_Calc_Figure_05_02_015.jpeg)
En el contexto del desplazamiento, el área neta señalizada nos permite tomar en cuenta la dirección. Si un automóvil viaja recto hacia el norte a una velocidad de 60 mph durante 2 horas, está a 120 millas al norte de su posición inicial. Si el automóvil luego da la vuelta y viaja hacia el sur a una velocidad de 40 mph durante 3 horas, volverá a su posición inicial (Figura\(\PageIndex{6}\)). Nuevamente, usando notación integral, tenemos
\[\int^2_060\,dt+∫^5_2−40\,dt=120−120=0.\nonumber \]
En este caso el desplazamiento es cero.
![Una gráfica en los cuadrantes uno y cuatro con el eje x etiquetado como t (horas) y el eje y etiquetado como v (mi/hr). La primera parte de la gráfica es la línea v (t) = 60 sobre [0,2], y el área debajo de la línea en el cuadrante uno está sombreada. La segunda parte de la gráfica es la línea v (t) = -40 sobre [2,5], y el área por encima de la línea en el cuadrante cuatro está sombreada.](https://math.libretexts.org/@api/deki/files/2591/CNX_Calc_Figure_05_02_016.jpeg)
Supongamos que queremos saber hasta qué punto viaja el automóvil en general, independientemente de la dirección. En este caso, queremos conocer el área entre la curva y el\(t\) eje -eje, independientemente de que esa área esté por encima o por debajo del eje. A esto se le llama el área total.
Gráficamente, es más fácil pensar en calcular el área total sumando las áreas por encima del eje y las áreas debajo del eje (en lugar de restar las áreas debajo del eje, como hicimos con el área con signo neto). Para lograrlo matemáticamente, utilizamos la función de valor absoluto. Así, la distancia total recorrida por el carro es
\[\int^2_0|60|\,dt+∫^5_2|−40|\,dt=∫^2_060\,dt+∫^5_240\,dt=120+120=240.\nonumber \]
Reuniendo formalmente estas ideas, exponemos las siguientes definiciones.
Let\(f(x)\) ser una función integrable definida en un intervalo\([a,b]\). Dejar\(A_1\) representar el área entre\(f(x)\) y el\(x\) -eje que se encuentra por encima del eje y dejar\(A_2\) representar el área entre\(f(x)\) y el\(x\) -eje que se encuentra por debajo del eje. Luego, el área neta firmada entre\(f(x)\) y el\(x\) eje está dada por
\[∫^b_af(x)\,dx=A_1−A_2. \nonumber \]
El área total entre\(f(x)\) y el\(x\) eje está dada por
\[∫^b_a|f(x)|\,dx=A_1+A_2. \nonumber \]
Encuentra el área total entre el eje\(f(x)=x−2\) y el\(x\) eje en el intervalo\([0,6].\)
Solución
Calcular la\(x\) -intercepción como\((2,0)\) (set\(y=0,\) solve for\(x\)). Para encontrar el área total, tome el área debajo del\(x\) eje -sobre el subintervalo\([0,2]\) y agréguela al área por encima del\(x\) eje -en el subintervalo\([2,6]\) (Figura\(\PageIndex{7}\)).
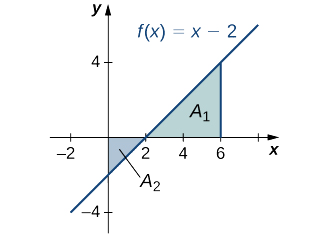
Tenemos
\[∫^6_0|(x−2)|\,dx=A_2+A_1. \nonumber \]
Luego, usando la fórmula para el área de un triángulo, obtenemos
\[A_2=\dfrac{1}{2}bh=\dfrac{1}{2}⋅2⋅2=2 \nonumber \]
\[A_1=\dfrac{1}{2}bh=\dfrac{1}{2}⋅4⋅4=8. \nonumber \]
El área total, entonces, es
\[A_1+A_2=8+2=10\,\text{units}^2. \nonumber \]
Encuentra el área total entre la función\(f(x)=2x\) y el\(x\) eje a lo largo del intervalo\([−3,3].\)
- Pista
-
Revisar la estrategia de resolución en Ejemplo\(\PageIndex{4}\).
- Contestar
-
\(18\,\text{units}^2\)
Propiedades de la Integral Definitiva
Las propiedades de las integrales indefinidas también se aplican a las integrales definidas. Las integrales definidas también tienen propiedades que se relacionan con los límites de la integración. Estas propiedades, junto con las reglas de integración que examinamos más adelante en este capítulo, nos ayudan a manipular expresiones para evaluar integrales definidas.
1. \[ \begin{equation} ∫^a_af(x)\,dx=0 \end{equation} \nonumber \]
Si los límites de integración son los mismos, la integral es solo una línea y no contiene área.
2. \[∫^a_bf(x)\,dx=−∫^b_af(x)\,dx \nonumber \]
Si los límites se invierten, entonces coloca un signo negativo frente a la integral.
3. \[∫^b_a[f(x)+g(x)]\,dx=∫^b_af(x)\,dx+∫^b_ag(x)\,dx \nonumber \]
La integral de una suma es la suma de las integrales.
4. \[∫^b_a[f(x)−g(x)]\,dx=∫^b_af(x)\,dx−∫^b_ag(x)\,dx \nonumber \]
La integral de una diferencia es la diferencia de las integrales.
5. \[∫^b_acf(x)\,dx=c∫^b_af(x)\,dx \nonumber \]
para constante\(c\). La integral del producto de una constante y una función es igual a la constante multiplicada por la integral de la función.
6. \[∫^b_af(x)\,dx=∫^c_af(x)\,dx+∫^b_cf(x)\,dx \nonumber \]
Aunque esta fórmula normalmente se aplica cuando\(c\) está entre\(a\) y\(b\), la fórmula se mantiene para todos los valores de\(a\),\(b\), y\(c\), siempre\(f(x)\) es integrable en el intervalo más grande.
Utilice las propiedades de la integral definida para expresar la integral definida de\(f(x)=−3x^3+2x+2\) sobre el intervalo\([−2,1]\) como la suma de tres integrales definidas.
Solución
Usando notación integral, tenemos\(\displaystyle ∫^1_{−2}(−3x^3+2x+2)\,dx.\) Aplicamos las propiedades 3. y 5. para obtener
\ [\ begin {align*} ^1_ {−2} (−3x^3+2x+2)\, dx =^1_ {−2} −3x^3\, dx+^1_ {−2} 2x\, dx+^1_ {−2} 2\, dx\ [4pt]
=−3^1_ {−2} x^3\, dx+2^1_ {−2} x\, dx+^1_ {−2} 2\, dx. \ end {align*}\ nonumber\]
Utilice las propiedades de la integral definida para expresar la integral definida de\(f(x)=6x^3−4x^2+2x−3\) sobre el intervalo\([1,3]\) como la suma de cuatro integrales definidas.
- Pista
-
Utilice la estrategia de resolución de\(\PageIndex{5}\) Example y las propiedades de integrales definidas.
- Contestar
-
\(\displaystyle 6∫^3_1x^3\,dx−4∫^3_1x^2\,dx+2∫^3_1x\,dx−∫^3_13\,dx \)
Si se sabe que\(\displaystyle ∫^8_0f(x)\,dx=10\) y\(\displaystyle ∫^5_0f(x)\,dx=5\), encontrar el valor de\(\displaystyle ∫^8_5f(x)\,dx\).
Solución
Por propiedad,
\[∫^b_af(x)\,dx=∫^c_af(x)\,dx+∫^b_cf(x)\,dx. \nonumber \]
Así,
\[ \begin{align*} ∫^8_0f(x)\,dx&=∫^5_0f(x)\,dx+∫^8_5f(x)\,dx \\[4pt] 10 &=5+∫^8_5f(x)\,dx \\[4pt] 5 &=∫^8_5f(x)\,dx. \end{align*}\]
Si se sabe que\(\displaystyle ∫^5_1f(x)\,dx=−3\) y\(\displaystyle ∫^5_2f(x)\,dx=4\), encontrar el valor de\(\displaystyle ∫^2_1f(x)\,dx.\)
- Pista
-
Usa la estrategia de resolución de\(\PageIndex{6}\) Example y la regla sobre propiedades de integrales definidas.
- Contestar
-
\(−7\)
Propiedades de Comparación de Integrales
Una imagen a veces puede decirnos más sobre una función que los resultados de los cálculos. La comparación de funciones tanto por sus gráficas como por sus expresiones algebraicas a menudo puede dar una nueva visión del proceso de integración. Intuitivamente, podríamos decir que si una función\(f(x)\) está por encima de otra función\(g(x)\), entonces el área entre\(f(x)\) y el\(x\) eje es mayor que el área entre\(g(x)\) y el\(x\) eje -eje. Esto es cierto dependiendo del intervalo a lo largo del cual se realice la comparación. Las propiedades de integrales definidas son válidas ya sea\(a<b,\,a=b\), o\(a>b\). Las siguientes propiedades, sin embargo, se refieren solo al caso\(a≤b\), y se utilizan cuando queremos comparar los tamaños de integrales.
i. Si es\(f(x)≥0\) por\(a≤x≤b\), entonces
\[∫^b_af(x)\,dx≥0. \nonumber \]
ii. Si es\(f(x)≥g(x)\) por\(a≤x≤b\), entonces
\[∫^b_af(x)\,dx≥∫^b_ag(x)\,dx. \nonumber \]
iii. Si\(m\) y\(M\) son constantes tales que\(m≤f(x)≤M\) para\(a≤x≤b\), entonces
\[m(b−a)≤∫^b_af(x)\,dx≤M(b−a). \nonumber \]
Comparar\(f(x)=\sqrt{1+x^2}\) y\(g(x)=\sqrt{1+x}\) a lo largo del intervalo\([0,1]\).
Solución
Graficar estas funciones es necesario para entender cómo se comparan a lo largo del intervalo\([0,1].\) Inicialmente, cuando se grafica en una calculadora gráfica,\(f(x)\) parece estar por encima de\(g(x)\) todas partes. Sin embargo, en el intervalo\([0,1]\), las gráficas parecen estar una encima de la otra. Necesitamos acercar para ver eso, en el intervalo\([0,1],\,g(x)\) está arriba\(f(x)\). Las dos funciones se cruzan en\(x=0\) y\(x=1\) (Figura\(\PageIndex{8}\)).
![Una gráfica de la función f (x) = sqrt (1 + x^2) en rojo y g (x) = sqrt (1 + x) en azul sobre [-2, 3]. La función f (x) aparece por encima de g (x) excepto en el intervalo [0,1]. Una segunda gráfica ampliada muestra este intervalo con mayor claridad.](https://math.libretexts.org/@api/deki/files/12425/5.2.5.png)
Podemos ver en la gráfica que a lo largo del intervalo\([0,1],\,g(x)≥f(x)\). Comparando las integrales a lo largo del intervalo especificado también\([0,1],\) vemos eso\(\displaystyle ∫^1_0g(x)\,dx≥∫^1_0f(x)\,dx\) (Figura\(\PageIndex{9}\)). El área delgada y sombreada en rojo muestra cuánta diferencia hay entre estas dos integrales a lo largo del intervalo\([0,1].\)
![Una gráfica que muestra las funciones f (x) = sqrt (1 + x^2) y g (x) = sqrt (1 + x) sobre [-3, 3]. El área bajo g (x) en el cuadrante uno sobre [0,1] está sombreada. El área bajo g (x) y f (x) se incluye en esta área sombreada. La segunda gráfica ampliada muestra con mayor claridad que la igualdad entre las funciones solo se mantiene en los puntos finales.](https://math.libretexts.org/@api/deki/files/12426/5.2.6.png)
Valor promedio de una función
A menudo necesitamos encontrar el promedio de un conjunto de números, como una calificación promedio de prueba. Supongamos que recibió los siguientes puntajes de prueba en su clase de álgebra: 89, 90, 56, 78, 100 y 69. Tu calificación semestral es tu promedio de puntajes de exámenes y quieres saber qué calificación esperar. Podemos encontrar el promedio sumando todas las puntuaciones y dividiendo por el número de puntajes. En este caso, hay seis puntajes de exámenes. Así,
\[\dfrac{89+90+56+78+100+69}{6}=\dfrac{482}{6}≈80.33. \nonumber \]
Por lo tanto, tu nota promedio de examen es de aproximadamente 80.33, lo que se traduce en una B − en la mayoría de las escuelas.
Supongamos, sin embargo,\(v(t)\) que tenemos una función que nos da la velocidad de un objeto en cualquier momento\(t\), y queremos encontrar la velocidad promedio del objeto. La función\(v(t)\) adquiere un número infinito de valores, por lo que no podemos usar el proceso que acabamos de describir. Afortunadamente, podemos usar una integral definida para encontrar el valor promedio de una función como esta.
Dejar\(f(x)\) ser continuo a lo largo del intervalo\([a,b]\) y dejar\([a,b]\) ser dividido en n subintervalos de ancho\(Δx=(b−a)/n\). Elija un representante\(x^∗_i\) en cada subintervalo y calcule\(f(x^∗_i)\) para\(i=1,2,…,n.\) En otras palabras, considere cada uno\(f(x^∗_i)\) como un muestreo de la función sobre cada subintervalo. El valor promedio de la función puede entonces aproximarse como
\[f_{ave} \approx \dfrac{f(x^∗_1)+f(x^∗_2)+⋯+f(x^∗_n)}{n}, \nonumber \]
que es básicamente la misma expresión utilizada para calcular el promedio de los valores discretos.
Pero\(Δx=\dfrac{b−a}{n},\) lo sabemos\(n=\dfrac{b−a}{Δx}\), y obtenemos
\[f_{ave} \approx \dfrac{f(x^∗_1)+f(x^∗_2)+⋯+f(x^∗_n)}{n}=\dfrac{f(x^∗_1)+f(x^∗_2)+⋯+f(x^∗_n)}{\left(\dfrac{b−a}{Δx}\right)}. \nonumber \]
Siguiendo con el álgebra, el numerador es una suma que se representa como\(\sum_{i=1}^nf(x∗i),\) y estamos dividiendo por una fracción. Para dividir por una fracción, invertir el denominador y multiplicar. Así, un valor aproximado para el valor promedio de la función viene dado por
\[\dfrac{\sum_{i=1}^nf(x^∗_i)}{\left(\dfrac{b−a}{Δx}\right)}=\left(\dfrac{Δx}{b−a}\right)\sum_{i=1}^nf(x^∗_i)=\left(\dfrac{1}{b−a}\right)\sum_{i=1}^nf(x^∗_i)Δx. \nonumber \]
Se trata de una suma de Riemann. Entonces, para obtener el valor promedio exacto, toma el límite como\(n\) va al infinito. Así, el valor promedio de una función viene dado por
\[\dfrac{1}{b−a}\lim_{n→∞}\sum_{i=1}^nf(x_i)Δx=\dfrac{1}{b−a}∫^b_af(x)dx. \nonumber \]
Dejar\(f(x)\) ser continuo a lo largo del intervalo\([a,b]\). Entonces, el valor promedio de la función\(f(x)\) (o\(f_{ave}\)) on\([a,b]\) viene dado por
\[f_{ave}=\dfrac{1}{b−a}∫^b_af(x)\,dx. \label{averagevalue} \]
Encuentra el valor promedio de\(f(x)=x+1\) sobre el intervalo\([0,5].\)
Solución
Primero, graficar la función en el intervalo establecido, como se muestra en la Figura\(\PageIndex{10}\).
![Una gráfica en el cuadrante uno que muestra el área sombreada bajo la función f (x) = x + 1 sobre [0,5].](https://math.libretexts.org/@api/deki/files/12427/5.2.7.png)
La región es un trapecio tendido de lado, por lo que podemos usar la fórmula de área para un trapecio\(A=\dfrac{1}{2}h(a+b),\) donde\(h\) representa la altura,\(a\) y y\(b\) representar los dos lados paralelos. Entonces,
\(\displaystyle ∫^5_0x+1\,dx=\dfrac{1}{2}h(a+b)=\dfrac{1}{2}⋅5⋅(1+6)=\dfrac{35}{2}\).
Así, el valor promedio de la función es
\(\displaystyle \dfrac{1}{5−0}∫^5_0x+1\,dx=\dfrac{1}{5}⋅\dfrac{35}{2}=\dfrac{7}{2}\).
Encuentra el valor promedio de\(f(x)=6−2x\) sobre el intervalo\([0,3].\)
- Pista
-
Utilice la fórmula del valor promedio (Ecuación\ ref {valor medio}) y utilice la geometría para evaluar la integral.
- Contestar
-
\(3\)
Conceptos clave
- La integral definida se puede utilizar para calcular el área neta firmada, que es el área por encima del\(x\) eje menos el área por debajo del\(x\) eje. El área neta firmada puede ser positiva, negativa o cero.
- Las partes componentes de la integral definida son el integrando, la variable de integración y los límites de la integración.
- Las funciones continuas en un intervalo cerrado son integrables. Las funciones que no son continuas pueden seguir siendo integrables, dependiendo de la naturaleza de las discontinuidades.
- Las propiedades de integrales definidas se pueden utilizar para evaluar integrales.
- El área bajo la curva de muchas funciones se puede calcular usando fórmulas geométricas.
- El valor promedio de una función se puede calcular utilizando integrales definidas.
Ecuaciones Clave
- Integral Definitiva
\(\displaystyle∫^b_af(x)\,dx=\lim_{n→∞}\sum_{i=1}^nf(x^∗_i)Δx\)
- Propiedades de la Integral Definitiva
\(\displaystyle∫^a_af(x)\,dx=0\)
\(\displaystyle∫^a_bf(x)\,dx=−∫^b_af(x)\,dx\)
\(\displaystyle∫^b_a[f(x)+g(x)]\,dx=∫^b_af(x)\,dx+∫^b_ag(x)\,dx\)
\(\displaystyle∫^b_a[f(x)−g(x)]\,dx=∫^b_af(x)\,dx−∫^b_ag(x)\,dx\)
\(\displaystyle∫^b_acf(x)\,dx=c∫^b_af(x)\,dx\), para constante\(c\)
\(\displaystyle∫^b_af(x)\,dx=∫^c_af(x)\,dx+∫^b_cf(x)\,dx\)
Glosario
- valor promedio de una función
- (o\(f_{ave})\) el valor promedio de una función en un intervalo se puede encontrar calculando la integral definida de la función y dividiendo ese valor por la longitud del intervalo
- integral definida
- una operación primaria de cálculo; el área entre la curva y el\(x\) eje en un intervalo dado es una integral definida
- función integrable
- una función es integrable si existe el límite que define la integral; en otras palabras, si existe el límite de las sumas de Riemann como\(n\) va al infinito
- integrand
- la función a la derecha del símbolo de integración; el integrando incluye la función que se integra
- límites de integración
- estos valores aparecen cerca de la parte superior e inferior del signo integral y definen el intervalo sobre el cual se debe integrar la función
- área neta firmada
- el área entre una función y el\(x\) eje de tal manera que el área debajo\(x\) del eje -se resta del área por encima del\(x\) eje -; el resultado es el mismo que la integral definida de la función
- área total
- el área total entre una función y el\(x\) eje -se calcula sumando el área por encima\(x\) del eje -y el área por debajo\(x\) del eje -; el resultado es el mismo que la integral definida del valor absoluto de la función
- variable de integración
- indica a qué variable estás integrando con respecto; si lo es\(x\), entonces la función en el integrando va seguida de\(dx\)


