5.3: Sumas de Riemann

En la sección anterior definimos la integral definida de una función en$[a,b]$ como el área firmada entre la curva y$x$ el eje. Algunas áreas eran sencillas de calcular; terminamos la sección con una región cuya área no era sencilla de calcular. En esta sección desarrollamos una técnica para encontrar tales áreas.

Una técnica de cálculo fundamental es primero responder a un problema dado con una aproximación, luego refinar esa aproximación para mejorarla, luego usar límites en el proceso de refinación para encontrar la respuesta exacta. Eso es exactamente lo que vamos a hacer aquí.

Considerar la región dada en la Figura$\PageIndex{1}$, que es el área bajo$y=4x-x^2$ on$[0,4]$. ¿Cuál es el área firmada de esta región, es decir, qué es$\int_0^4(4x-x^2)dx$?

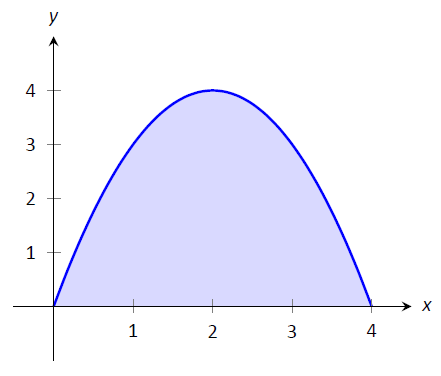
Figura$\PageIndex{1}$: Una gráfica de$f(x) = 4x-x^2$. ¿Cuál es el área de la región sombreada?

Empezamos por aproximar. Podemos rodear la región con un rectángulo con altura y ancho de 4 y encontrar el área es de aproximadamente 16 unidades cuadradas. Esto es obviamente una sobreaproximación; estamos incluyendo área en el rectángulo que no está debajo de la parábola.

Tenemos una aproximación del área, usando un rectángulo. ¿Cómo podemos refinar nuestra aproximación para mejorarla? La clave de esta sección es esta respuesta: usar más rectángulos.

Usemos 4 rectángulos de igual ancho de 1. Esto divide el intervalo$[0,4]$ en 4 subintervalos,$[0,1]$,$[1,2]$,$[2,3]$ y$[3,4]$. En cada subintervalo dibujaremos un rectángulo.

Hay tres formas comunes de determinar la altura de estos rectángulos: la Regla de la Mano Izquierda, la Regla de la Mano Derecha y la Regla del Punto Medio. La regla de la mano izquierda dice evaluar la función en el punto final izquierdo—mano del subintervalo y hacer el rectángulo esa altura. En Figura$\PageIndex{2}$, el rectángulo dibujado en el intervalo$[2,3]$ tiene altura determinada por la Regla de la Mano Izquierda; tiene una altura de$f(2)$. (El rectángulo está etiquetado como “LHR”).

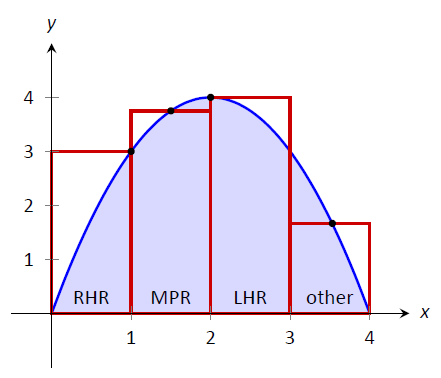
Figura$\PageIndex{2}$: Aproximación$\int_0^4(4x-x^2)dx$ mediante rectángulos. Las alturas de los rectángulos se determinan usando diferentes reglas.

La regla de la mano derecha dice lo contrario: en cada subintervalo, evalúe la función en el punto final derecho y haga el rectángulo esa altura. En la figura, el rectángulo dibujado$[0,1]$ se dibuja usando$f(1)$ como su altura; este rectángulo se etiqueta “RHR”.

La Regla de Punto Medio dice que en cada subintervalo, evaluar la función en el punto medio y hacer el rectángulo esa altura. El rectángulo sobre el que se$[1,2]$ dibujó se realizó utilizando la Regla de Punto Medio, con una altura de$f(1.5)$. Ese rectángulo está etiquetado como “MPR”.

Estas son las tres reglas más comunes para determinar las alturas de los rectángulos aproximados, pero una no se ve obligada a utilizar uno de estos tres métodos. El rectángulo$[3,4]$ tiene una altura de aproximadamente$f(3.53)$, muy cerca de la Regla del Punto Medio. Se eligió para que el área del rectángulo sea exactamente el área de la región debajo$f$ en$[3,4]$. (Más tarde también podrás averiguar cómo hacer esto).

El siguiente ejemplo aproximará el valor de$\int_0^4 (4x-x^2)dx$ usar estas reglas.

Ejemplo$\PageIndex{1}$: Using the Left Hand, Right Hand and Midpoint Rules

Aproximar el valor de$\int_0^4 (4x-x^2)dx$ usar la Regla de Mano Izquierda, la Regla de Mano Derecha y la Regla de Punto Medio, usando 4 subintervalos igualmente espaciados.

Solución

{Rompemos el intervalo$[0,4]$ en cuatro subintervalos como antes. En la Figura$\PageIndex{3}$ vemos 4 rectángulos dibujados$f(x) = 4x-x^2$ usando la Regla de la Mano Izquierda. (Las áreas de los rectángulos se dan en cada figura.)

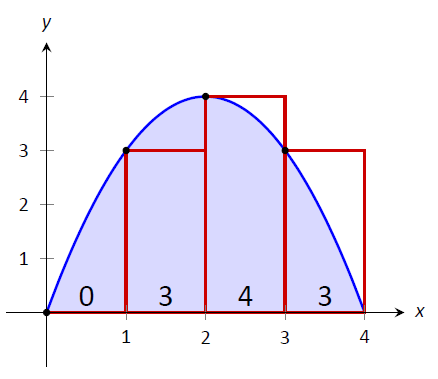
Figura$\PageIndex{3}$: Aproximación$\int_0^4(4x-x^2)dx$ usando la regla de la mano izquierda en el ejemplo$\PageIndex{1}$

Observe cómo en el primer subintervalo,$[0,1]$, el rectángulo tiene altura$f(0)=0$. Sumamos las áreas de cada rectángulo (alto$\times$ ancho) para nuestra aproximación de Regla de Mano Izquierda:

$$\begin{align} f(0)\cdot 1 + f(1)\cdot 1+ f(2)\cdot 1+f(3)\cdot 1 &=\\ 0+3+4+3&= 10. \end{align}$$

La Figura$\PageIndex{4}$ muestra 4 rectángulos dibujados bajo$f$ usando la Regla de la Mano Derecha; observe cómo el$[3,4]$ subintervalo tiene un rectángulo de altura 0.

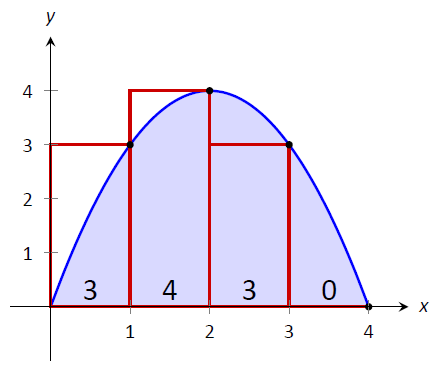
Figura$\PageIndex{4}$: Aproximación$\int_0^4(4x-x^2)dx$ usando la regla de la mano derecha en el ejemplo$\PageIndex{1}$

En este ejemplo, estos rectángulos parecen ser la imagen especular de los que se encuentran en la Figura$\PageIndex{3}$. (Esto se debe a la simetría de nuestra región sombreada.) Nuestra aproximación da la misma respuesta que antes, aunque calculada de una manera diferente:

$$\begin{align} f(1)\cdot 1 + f(2)\cdot 1+ f(3)\cdot 1+f(4)\cdot 1 &=\\ 3+4+3+0&= 10. \end{align}$$

La figura$\PageIndex{5}$ muestra 4 rectángulos dibujados bajo$f$ usando la Regla de Punto Medio.

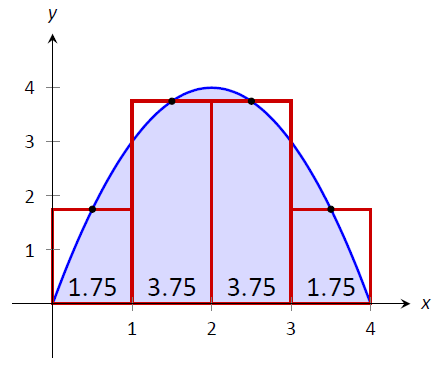
Figura$\PageIndex{5}$: Aproximación$\int_0^4(4x-x^2)dx$ usando la regla de punto medio en el ejemplo$\PageIndex{1}$

Esto da una aproximación de$\int_0^4(4x-x^2)dx$ como:

$$\begin{align} f(0.5)\cdot 1 + f(1.5)\cdot 1+ f(2.5)\cdot 1+f(3.5)\cdot 1 &=\\ 1.75+3.75+3.75+1.75&= 11. \end{align}$$

Nuestros tres métodos proporcionan dos aproximaciones de$\int_0^4(4x-x^2)dx$: 10 y 11.

Notación de suma

Es difícil decir en este momento cuál es una mejor aproximación: ¿10 u 11? Podemos seguir refinando nuestra aproximación usando más rectángulos. Sin embargo, la notación puede volverse difícil de manejar, ya que sumamos listas de números cada vez más largas. Introducimos notación de suma para mejorar este problema.

Supongamos que deseamos sumar una lista de números$a_1$,$a_2$,$a_3$,\ ldots,$a_9$. En lugar de escribir

$a_1+a_2+a_3+a_4+a_5+a_6+a_7+a_8+a_9,\]

usamos notación de suma y escribimos

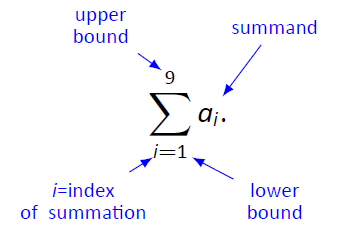
Figura$\PageIndex{6}$: Comprensión de la notación de suma

La sigma mayúscula representa el término “suma”. El índice de suma en este ejemplo es$i$; se puede usar cualquier símbolo. Por convención, el índice toma solo los valores enteros entre (e incluyendo) los límites inferior y superior.

Practicemos usando esta notación.

Ejemplo$\PageIndex{2}$: Using summation notation

Deje que los números$\{a_i\}$ se definan como$a_i = 2i-1$ para enteros$i$, donde$i\geq 1$. Entonces$a_1 = 1$,$a_2 = 3$,$a_3 = 5$, etc. (La salida son los enteros impares positivos). Evalúe las siguientes sumas:

$$1.\ \sum_{i=1}^6 a_i \qquad\qquad\qquad 2.\ \sum_{i=3}^7 (3a_i-4)\qquad\qquad \qquad 3.\ \sum_{i=1}^4 (a_i)^2$$

Solución

1. $$\begin{align} \sum_{i=1}^6 a_i &= a_1+a_2+a_3+a_4+a_5+a_6\\ &= 1+3+5+7+9+11 \\ &= 36.\end{align}$$
2. Tenga en cuenta que el valor inicial es diferente a 1: $$\begin{align} \sum_{i=3}^7 a_i &= (3a_3-4)+(3a_4-4)+(3a_5-4)+(3a_6-4)+(3a_7-4) \\ &= 11+17+23+29+35 \\ &= 115. \end{align}$$
3. $$\begin{align} \sum_{i=1}^4 (a_i)^2 &= (a_1)^2+(a_2)^2+(a_3)^2+(a_4)^2\\ &= 1^2+3^2+5^2+7^2 \\ &= 84 \end{align}$$

Puede parecer extraño enfatizar una forma nueva y concisa de escribir sumaciones solo para escribir cada término a medida que los sumamos. Lo es. El siguiente teorema da algunas de las propiedades de las sumaciones que nos permiten trabajar con ellas sin escribir términos individuales. A continuación se darán ejemplos.

Teorema$\PageIndex{1}$: Properties of Summations

1. $\sum_{i=1}^n c = c\cdot n$, donde$c$ es una constante.
2. $\sum_{i=m}^n (a_i\pm b_i) = \sum_{i=m}^n a_i \pm \sum_{i=m}^n b_i$
3. $\sum_{i=m}^n c\cdot a_i = c\cdot\sum_{i=m}^n a_i$
4. $\sum_{i=m}^j a_i + \sum_{i=j+1}^n a_i = \sum_{i=m}^n a_i$
5. $\sum_{i=1}^n i = \frac{n(n+1)}2$
6. $\sum_{i=1}^n i^2 = \frac{n(n+1)(2n+1)}6$
7. $\sum_{i=1}^n i^3 = \left(\frac{n(n+1)}2\right)^2$

Ejemplo$\PageIndex{3}$: Evaluating summations using Theorem$\PageIndex{1}$

Revisite el Ejemplo$\PageIndex{2}$ y, usando el Teorema$\PageIndex{1}$, evalúe

$$\sum_{i=1}^6 a_i = \sum_{i=1}^6 (2i-1).$$

Solución

$$\begin{align} \sum_{i=1}^6 (2i-1) & = \sum_{i=1}^6 2i - \sum_{i=1}^6 (1)\\ &= \left(2\sum_{i=1}^6 i \right)- 6 \\ &= 2\frac{6(6+1)}{2} - 6 \\ &= 42-6 = 36 \end{align}$$

Obtuvimos la misma respuesta sin escribir los seis términos. Cuando se trata de tamaños pequeños de$n$, puede ser más rápido escribir los términos a mano. Sin embargo, el teorema$\PageIndex{1}$ es increíblemente importante a la hora de tratar con grandes sumas como pronto veremos.

Sumas de Riemann

Considerar de nuevo$\int_0^4(4x-x^2)dx$. Aproximaremos esta integral definida usando 16 subintervalos igualmente espaciados y la Regla de la Mano Derecha en Ejemplo$\PageIndex{4}$. Antes de hacerlo, pagará hacer una cuidadosa preparación.

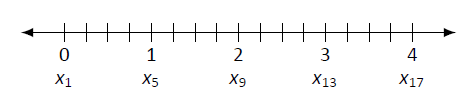
Figura$\PageIndex{7}$: Dividiendo$[0,4]$ en 16 subintervalos igualmente espaciados.

La figura$\PageIndex{7}$ muestra una línea numérica$[0,4]$ dividida en 16 subintervalos igualmente espaciados. Denotamos$0$ como$x_1$; hemos marcado los valores de$x_5$,$x_9$,$x_{13}$ y$x_{17}$. Podríamos marcarlos a todos, pero la cifra se abarrotaría. Si bien es fácil imaginar que$x_{10} = 2.25$, en general, queremos un método para determinar el valor de$x_i$ sin consultar la figura. Considerar:

Entonces$x_{10} = x_1 + 9(4/16) = 2.25.$

Si hubiéramos particionado$[0,4]$ en 100 subintervalos igualmente espaciados, cada subintervalo tendría longitud$\Delta x=4/100 = 0.04$. Podríamos computar$x_{32}$ como

$$x_ {32} = x_1 + 31 (4/100) = 1.24.\]

(Eso fue mucho más rápido que crear un boceto primero).

Dada cualquier subdivisión de$[0,4]$, el primer subintervalo es$[x_1,x_2]$; el segundo es$[x_2,x_3]$; el$i^\text{ th}$ subintervalo es$[x_i,x_{i+1}]$.

Al usar la Regla de la Mano Izquierda, la altura del$i^\text{ th}$ rectángulo será$f(x_i)$.

Al usar la Regla de la Mano Derecha, la altura del$i^\text{ th}$ rectángulo será$f(x_{i+1})$.

Al usar la Regla de Punto Medio, la altura del$i^\text{ th}$ rectángulo será$f\left(\frac{x_i+x_{i+1}}2\right)$.

Así, aproximándose$\int_0^4(4x-x^2)dx$ con 16 subintervalos equidistantes se puede expresar de la siguiente manera, donde$\Delta x = 4/16 = 1/4$:

Regla de la mano izquierda:$\sum_{i=1}^{16} f(x_i)\Delta x$

Regla de la mano derecha:$\sum_{i=1}^{16} f(x_{i+1})\Delta x$

Regla de punto medio:$\sum_{i=1}^{16} f\left(\frac{x_i+x_{i+1}}2\right)\Delta x$

Utilizamos estas fórmulas en los siguientes dos ejemplos. El siguiente ejemplo nos permite practicar usando la Regla de la Mano Derecha y las fórmulas de suma introducidas en el Teorema$\PageIndex{1}$

Ejemplo$\PageIndex{4}$: Approximating definite integrals using sums

Aproximar$\int_0^4(4x-x^2)dx$ usando la Regla de la Mano Derecha y fórmulas de suma con 16 y 1000 intervalos igualmente espaciados.

Solución

Usando la fórmula derivada antes, usando 16 intervalos igualmente espaciados y la Regla de la Mano Derecha, podemos aproximar la integral definida como

$$\sum_{i=1}^{16}f(x_{i+1})\Delta x.$$

Tenemos$\Delta x = 4/16 = 0.25$. Desde entonces$x_i = 0+(i-1)\Delta x$, tenemos

$$\begin{align}x_{i+1} &= 0 + \big((i+1)-1\big)\Delta x \\ &= i\Delta x \end{align}$$

Usando las fórmulas de suma, considere:

$$\begin{align} \int_0^4 (4x-x^2)dx &\approx \sum_{i=1}^{16} f(x_{i+1})\Delta x \\ &= \sum_{i=1}^{16} f(i\Delta x) \Delta x\\ &= \sum_{i=1}^{16} \big(4i\Delta x - (i\Delta x)^2\big)\Delta x\\ &= \sum_{i=1}^{16} (4i\Delta x^2 - i^2\Delta x^3)\\ &= (4\Delta x^2)\sum_{i=1}^{16} i - \Delta x^3 \sum_{i=1}^{16} i^2 \\ &= (4\Delta x^2)\frac{16\cdot 17}{2} - \Delta x^3 \frac{16(17)(33)}6 \\ &= 4\cdot 0.25^2\cdot 136-0.25^3\cdot 1496\\ &=10.625 \end{align}$$

Pudimos resumir las áreas de 16 rectángulos con muy poco cálculo. En$\PageIndex{8}$ la Figura se grafican la función y los 16 rectángulos. Mientras que algunos rectángulos sobre-aproximan el área, otros subaproximan el área (aproximadamente en la misma cantidad). Por lo tanto, nuestra área aproximada de 10.625 es probablemente una aproximación bastante buena.

Observe la ecuación$\PageIndex{31}$; cambiando los 16 a 1,000 (y cambiando apropiadamente el valor de$\Delta x$), ¡podemos usar esa ecuación para sumar 1000 rectángulos!

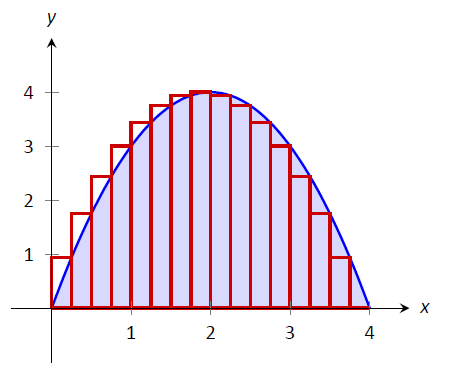
Figura$\PageIndex{8}$: Aproximación$\int_0^4(4x-x^2)dx$ con la Regla de la Mano Derecha y 16 subintervalos uniformemente espaciados.

Lo hacemos aquí, saltando de la suma original al equivalente de Ecuación$\PageIndex{31}$ para ahorrar espacio. Tenga en cuenta que$\Delta x = 4/1000 = 0.004$.

$$\begin{align} \int_0^4 (4x-x^2)dx &\approx \sum_{i=1}^{1000} f(x_{i+1})\Delta x \\&= (4\Delta x^2)\sum_{i=1}^{1000} i - \Delta x^3 \sum_{i=1}^{1000} i^2 \\&= (4\Delta x^2)\frac{1000\cdot 1001}{2} - \Delta x^3 \frac{1000(1001)(2001)}6 \\&= 4\cdot 0.004^2\cdot 500500-0.004^3\cdot 333,833,500\\ &=10.666656 \end{align}$$

Usando muchos, muchos rectángulos, tenemos probablemente una buena aproximación de$\int_0^4 (4x-x^2) dx$. Es decir,

$$\ int_0^4 (4x-x^2) dx\ aprox 10.666656.\]

Antes del ejemplo anterior, dijimos cómo se veían las sumas para las Reglas de Mano Izquierda, Mano Derecha y Punto Medio. Cada uno tenía la misma estructura básica, que era:

1. cada rectángulo tiene el mismo ancho, que nos referimos como$\Delta x$, y
2. la altura de cada rectángulo se determina evaluando$f$ en un punto particular en cada subintervalo. Por ejemplo, la Regla de la Mano Izquierda establece que la altura de cada rectángulo se determina evaluando$f$ en el extremo izquierdo del subintervalo en el que vive el rectángulo.

Se podría particionar un intervalo$[a,b]$ con subintervalos que no tuvieran el mismo tamaño. Nos referimos a la longitud del primer subintervalo como$\Delta x_1$, la longitud del segundo subintervalo como$\Delta x_2$, y así sucesivamente, dando la longitud del$i^\text{ th}$ subintervalo como$\Delta x_i$. Además, se podría determinar la altura de cada rectángulo evaluando$f$ en\ emph {any} punto en el$i^\text{ th}$ subintervalo. Nos referimos al punto escogido en el primer subintervalo como$c_1$, el punto escogido en el segundo subintervalo como$c_2$, y así sucesivamente, con la$c_i$ representación del punto escogido en el$i^\text{ th}$ subintervalo. Así la altura del$i^\text{ th}$ subintervalo sería$f(c_i)$, y el área del$i^\text{ th}$ rectángulo sería$f(c_i)\Delta x_i$.

Las sumaciones de rectángulos con área$f(c_i)\Delta x_i$ llevan el nombre del matemático Georg Friedrich Bernhard Riemann, como se da en la siguiente definición.

Definición$\PageIndex{1}$: Riemann Sum

Dejar$f$ ser definido en el intervalo cerrado$[a,b]$ y dejar$\Delta x$ ser una partición de$[a,b]$, con

$$a=x_1 < x_2 <\ ldots < x_n < x_ {n+1} =b.\]

Dejar$\Delta x_i$ denotar la longitud del$i^\text{ th}$ subintervalo$[x_i,x_{i+1}]$ y dejar$c_i$ denotar cualquier valor en el$i^\text{ th}$ subintervalo.

La suma

$$\ suma_ {i=1} ^n f (c_i)\ Delta x_i\]

es una suma de Riemann de$f$ on$[a,b]$.

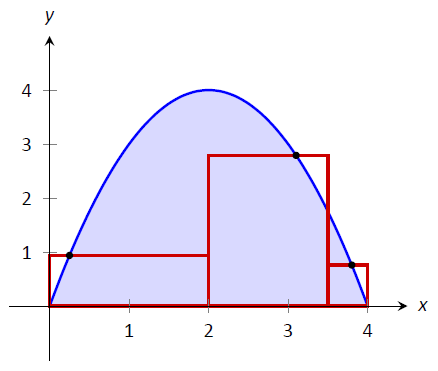
Figura$\PageIndex{9}$: Un ejemplo de una suma general de Riemann para aproximarse$\int_0^4(4x-x^2)dx$

La figura$\PageIndex{9}$ muestra los rectángulos aproximados de una suma de Riemann de$\int_0^4(4x-x^2)dx$. Si bien los rectángulos en este ejemplo no se aproximan bien al área sombreada, demuestran que los anchos del subintervalo pueden variar y las alturas de los rectángulos se pueden determinar sin seguir una regla particular.

“Por lo general” las sumas de Riemann se calculan utilizando uno de los tres métodos que hemos introducido. La uniformidad de la construcción facilita los cálculos. Antes de trabajar otro ejemplo, vamos a resumir algo de lo que hemos aprendido de una manera conveniente.

Idea clave 8: Conceptos de suma de Riemann

Considerar$\int_a^b f(x) dx \approx \sum_{i=1}^n f(c_i)\Delta x_i.$

1. Cuando los$n$ subintervalos tienen la misma longitud,$\Delta x_i = \Delta x = \frac{b-a}n.$
2. El$i^\text{ th}$ término de la partición es$x_i = a + (i-1)\Delta x$. (Esto hace$x_{n+1} = b$.)
3. La suma de la Regla de la Mano Izquierda es:$\sum_{i=1}^n f(x_i)\Delta x$.
4. La suma de la Regla de la Mano Derecha es:$\sum_{i=1}^n f(x_{i+1})\Delta x$.
5. La suma de la Regla de Punto Medio es:$\sum_{i=1}^n f\left(\frac{x_i+x_{x+1}}{2}\right)\Delta x$.

Hagamos otro ejemplo.

Ejemplo$\PageIndex{5}$: Approximating definite integrals with sums

Aproximado$\int_{-2}^3 (5x+2)dx$ usando la Regla de Punto Medio y 10 intervalos igualmente espaciados.

Solución

Siguiendo la Idea Clave 8, tenemos

$$\Delta x = \frac{3 - (-2)}{10} = 1/2 \quad \text{and} \quad x_i = (-2) + (1/2)(i-1) = i/2-5/2.$$

Como estamos usando la Regla de Punto Medio, también necesitaremos$x_{i+1}$ y$\frac{x_i+x_{i+1}}2$. Ya que$x_i = i/2-5/2$,$x_{i+1} = (i+1)/2 - 5/2 = i/2 -2$. Esto da

$$\frac{x_i+x_{i+1}}2 = \frac{(i/2-5/2) + (i/2-2)}{2} = \frac{i-9/2}{2} = i/2 - 9/4.$$

Ahora construimos la suma de Riemann y calculamos su valor usando fórmulas de suma.

$$\begin{align} \int_{-2}^3 (5x+2)dx &\approx \sum_{i=1}^{10} f\left(\frac{x_i+x_{i+1}}{2}\right)\Delta x \\ &= \sum_{i=1}^{10} f(i/2 - 9/4)\Delta x \\ &= \sum_{i=1}^{10} \big(5(i/2-9/4) + 2\big)\Delta x\\ &= \Delta x\sum_{i=1}^{10}\left[\left(\frac{5}{2}\right)i - \frac{37}{4}\right]\\ &= \Delta x\left(\frac{5}2\sum_{i=1}^{10} (i) - \sum_{i=1}^{10}\left(\frac{37}{4}\right)\right) \\&= \frac12\left(\frac52\cdot\frac{10(11)}{2} - 10\cdot\frac{37}4\right) \\ &= \frac{45}2 = 22.5 \end{align}$$

Observe la gráfica de$f(x) = 5x+2$ en la Figura$\PageIndex{10}$. Las regiones cuya área es calculada por la integral definida son triángulos, lo que significa que podemos encontrar la respuesta exacta sin técnicas de suma. Encontramos que la respuesta exacta es efectivamente 22.5. Una de las fortalezas de la Regla de Punto Medio es que a menudo cada rectángulo incluye área que no debe contarse, pero pierde otra área que debería. Cuando el tamaño de la partición es pequeño, estas dos cantidades son aproximadamente iguales y estos errores casi “se cancelan entre sí”. En este ejemplo, como nuestra función es una línea, estos errores son exactamente iguales y sí se cancelan entre sí, dándonos la respuesta exacta.

Tenga en cuenta también que cuando la función es negativa, los rectángulos tienen una altura “negativa”. Cuando calculamos el área del rectángulo, usamos$f(c_i)\Delta x$; cuando$f$ es negativo, el área se cuenta como negativa.

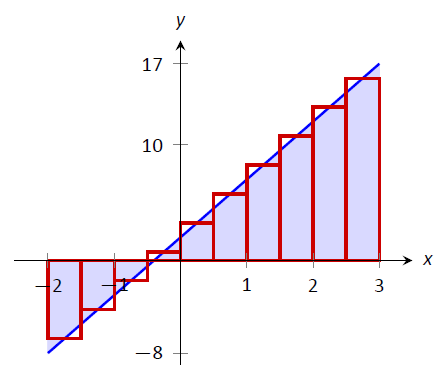
Figura$\PageIndex{10}$: Aproximación$\int_{-2}^3 (5x+2)dx$ usando la Regla de Punto Medio y 10 subintervalos uniformemente espaciados en Ejemplo$\PageIndex{5}$.

Observe en el ejemplo anterior que si bien usamos 10 intervalos igualmente espaciados, el número “10" no jugó un papel importante en los cálculos hasta el final. A los matemáticos les encanta abstraer ideas; aproximemos el área de otra región usando$n$ subintervalos, donde no especificamos un valor de$n$ hasta el final.

Ejemplo$\PageIndex{6}$: Approximating definite integrals with a formula, using sums

Vuelva a visitar una$\int_0^4(4x-x^2)dx$ vez más. Aproximar esta integral definida usando la Regla de la Mano Derecha con subintervalos$n$ igualmente espaciados.

Solución

Usando Key Idea 8, lo sabemos$\Delta x = \frac{4-0}{n} = 4/n$. También encontramos$x_i = 0 + \Delta x(i-1) = 4(i-1)/n$. La Regla de la Mano Derecha usa$x_{i+1}$, que es$x_{i+1} = 4i/n$.

Construimos la suma de Riemann de la Regla Derecha de la siguiente manera. Asegúrese de seguir cada paso cuidadosamente. Si te quedas atascado, y no entiendes cómo una línea pasa a la siguiente, puedes saltarte al resultado y considerar cómo se usa este resultado. Sin embargo, deberías regresar y trabajar en cada paso para lograr una comprensión completa.

$$\begin{align} \int_0^4(4x-x^2)dx &\approx \sum_{i=1}^n f(x_{i+1})\Delta x \\ &= \sum_{i=1}^n f\left(\frac{4i}{n}\right) \Delta x \\ &= \sum_{i=1}^n \left[4\frac{4i}n-\left(\frac{4i}n\right)^2\right]\Delta x\\ &= \sum_{i=1}^n \left(\frac{16\Delta x}{n}\right)i - \sum_{i=1}^n \left(\frac{16\Delta x}{n^2}\right)i^2 \\ &= \left(\frac{16\Delta x}{n}\right)\sum_{i=1}^n i - \left(\frac{16\Delta x}{n^2}\right)\sum_{i=1}^n i^2 \\ &= \left(\frac{16\Delta x}{n}\right)\cdot \frac{n(n+1)}{2} - \left(\frac{16\Delta x}{n^2}\right)\frac{n(n+1)(2n+1)}{6} &\left(\text{recall $\Delta x = 4/n$}\right)\\ &=\frac{32(n+1)}{n} - \frac{32(n+1)(2n+1)}{3n^2} &\text{(now simplify)} \\ &= \frac{32}{3}\left(1-\frac{1}{n^2}\right) \end{align}$$

El resultado es una fórmula increíble y fácil de usar. Para aproximar la integral definida con 10 subintervalos igualmente espaciados y la Regla de la Mano Derecha, establece$n=10$ y calcula

$$\ int_0^4 (4x-x^2) dx\ approx\ frac {32} {3}\ izquierda (1-\ frac {1} {10^2}\ derecha) = 10.56.\]

Recordemos cómo antes aproximamos la integral definida con 4 subintervalos; con$n=4$, la fórmula da 10, nuestra respuesta como antes.

¡Ahora es fácil aproximar la integral con 1,000,000 de subintervalos! Las calculadoras de mano completarán la respuesta un poco prematuramente dando una respuesta de$10.66666667$. (La respuesta real es$10.666666666656$.)

Ahora damos un salto importante. Hasta este punto, nuestras matemáticas se han limitado a la geometría y el álgebra (búsqueda de áreas y manipulación de expresiones). Ahora aplicamos\ textit {cálculo}. Para cualquier\ textit {finito}$n$, sabemos que

$$\ int_0^4 (4x-x^2) dx\ approx\ frac {32} {3}\ izquierda (1-\ frac {1} {n^2}\ derecha).\]

Tanto el sentido común como las matemáticas de alto nivel nos dicen que a medida$n$ que aumenta, la aproximación mejora. De hecho, si tomamos el límite como$n\rightarrow \infty$, obtenemos el área exacta descrita por$\int_0^4 (4x-x^2)dx$. Es decir,

$$\begin{align} \int_0^4 (4x-x^2)dx &= \lim_{n\rightarrow \infty} \frac{32}{3}\left(1-\frac{1}{n^2}\right) \\ &= \frac{32}{3}\left(1-0\right)\\ &= \frac{32}{3} = 10.\overline{6}\end{align}$$

Este es un resultado fantástico. Al considerar$n$ subintervalos igualmente espaciados, obtuvimos una fórmula para una aproximación de la integral definida que involucró nuestra variable$n$. $n$A medida que crece —sin límite— el error se reduce a cero y obtenemos el área exacta.

Esta sección comenzó con una técnica de cálculo fundamental: hacer una aproximación, refinar la aproximación para mejorarla, luego usar límites en el proceso de refinación para obtener una respuesta exacta. Eso es precisamente lo que acabamos de hacer.

Practicemos esto de nuevo.

Ejemplo$\PageIndex{7}$: Approximating definite integrals with a formula, using sums

Encuentra una fórmula que se aproxime$\int_{-1}^5 x^3dx$ usando la Regla de la Mano Derecha y subintervalos$n$ igualmente espaciados, luego toma el límite$n\to\infty$ para encontrar el área exacta.

Solución

Siguiendo la Idea Clave 8, tenemos$\Delta x = \frac{5-(-1)}{n} = 6/n$. Tenemos$x_i = (-1) + (i-1)\Delta x$; como usa la Regla de la Mano Derecha$x_{i+1}$, tenemos$x_{i+1} = (-1) + i\Delta x$.

La suma de Riemann correspondiente a la Regla de la Mano Derecha es (seguida de simplificaciones):

$$\begin{align}\int_{-1}^5 x^3dx &\approx \sum_{i=1}^n f(x_{i+1})\Delta x \\ &= \sum_{i=1}^n f(-1+i\Delta x)\Delta x \\ &= \sum_{i=1}^n (-1+i\Delta x)^3\Delta x \\&= \sum_{i=1}^n \big((i\Delta x)^3 -3(i\Delta x)^2 + 3i\Delta x -1\big)\Delta x \quad \text{\scriptsize (now distribute $\Delta x$)} \\ &= \sum_{i=1}^n \big(i^3\Delta x^4 - 3i^2\Delta x^3 + 3i\Delta x^2 -\Delta x\big) \quad \text{\scriptsize (now split up summation)}\\ &= \Delta x^4 \sum_{i=1}^ni^3 -3\Delta x^3 \sum_{i=1}^n i^2+ 3\Delta x^2 \sum_{i=1}^n i - \sum_{i=1}^n \Delta x \\ &= \Delta x^4 \left(\frac{n(n+1)}{2}\right)^2 -3\Delta x^3 \frac{n(n+1)(2n+1)}{6}+ 3\Delta x^2 \frac{n(n+1)}{2} - n\Delta x \\ \text{(use $\Delta x = 6/n$)}\\ &= \frac{1296}{n^4}\cdot\frac{n^2(n+1)^2}{4} - 3\frac{216}{n^3}\cdot\frac{n(n+1)(2n+1)}{6} + 3\frac{36}{n^2}\frac{n(n+1)}2 -6 \\ \text{(now do a sizable amount of algebra to simplify)}\\ &=156 + \frac{378}n + \frac{216}{n^2} \end{align}$$

Una vez más, hemos encontrado una fórmula compacta para aproximar la integral definida con subintervalos$n$ igualmente espaciados y la Regla de la Mano Derecha. Usando 10 subintervalos, tenemos una aproximación de$195.96$ (estos rectángulos se muestran en la Figura$\PageIndex{11}$. El uso$n=100$ da una aproximación de$159.802$.

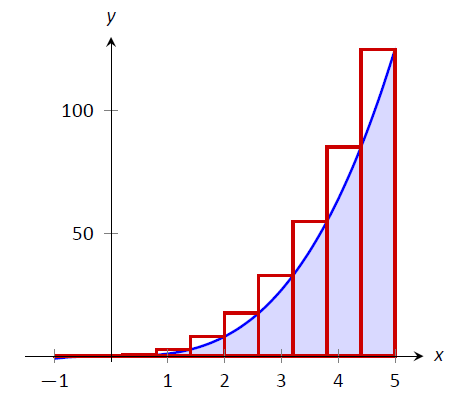
Figura$\PageIndex{11}$: Aproximación$\int_{-1}^5 x^3dx$ usando la Regla de la Mano Derecha y 10 subintervalos uniformemente espaciados.

Ahora encuentra la respuesta exacta usando un límite:

$$\ int_ {-1} ^5 x^3dx =\ lim_ {n\ a\ infty}\ izquierda (156 +\ frac {378} n +\ frac {216} {n^2}\ derecha) = 156.\]

Límites de las sumas de Riemann

Hemos utilizado límites para evaluar límites definidos exactamente dados. ¿Esto siempre funcionará? Demostraremos, dadas condiciones no muy restrictivas, que sí, siempre va a funcionar.

Los dos ejemplos anteriores demostraron cómo una expresión como

$$\ suma_ {i=1} ^n f (x_ {i+1})\ Delta x\]

se puede reescribir como una expresión que implique explícitamente$n$, como$32/3(1-1/n^2)$.

Visto de esta manera, podemos pensar en la suma como una función de$n$. Se da un$n$ valor (donde$n$ es un entero positivo), y se devuelve la suma de áreas de rectángulos$n$ equidistantes, usando las Reglas de Mano Izquierda, Mano Derecha o Punto Medio.

Dada una integral definida$\int_a^b f(x)dx$, dejemos:

1. $S_L(n) = \sum_{i=1}^n f(x_i)\Delta x$, la suma de rectángulos equidistantes formados usando la Regla de la Mano Izquierda,
2. $S_R(n) = \sum_{i=1}^n f(x_{i+1})\Delta x$, la suma de rectángulos equidistantes formados usando la Regla de la Mano Derecha, y
3. $S_M(n) = \sum_{i=1}^n f\left(\frac{x_i+x_{i+1}}{2}\right)\Delta x$, la suma de rectángulos equidistantes formados usando la Regla de Punto Medio.

Recordemos la definición de un límite como$n\to\infty$:$\lim_{n\to\infty}S_L(n) = K$ si, dado alguno$\epsilon>0$, existe$N>0$ tal que

$$\ izquierda|s_l (n) -K\ derecha| <\ épsilon\ quad\ texto {cuando}\ quad n\ geq N.\]

El siguiente teorema establece que podemos usar cualquiera de nuestras tres reglas para encontrar el valor exacto de una integral definida$\int_a^b f(x)dx$. También va dos pasos más allá. El teorema establece que la altura de cada rectángulo no tiene que ser determinada siguiendo una regla específica, sino que podría ser$f(c_i)$, donde$c_i$ está cualquier punto en el$i^\text{ th}$ subintervalo, como se discutió antes de Riemann Sumas donde se definieron en Definición$\PageIndex{1}$.

El teorema continúa afirmando que los rectángulos no necesitan ser del mismo ancho. Usando la notación de Definición$\PageIndex{1}$, vamos a$\Delta x_i$ denotar la longitud del$i^\text{ th}$ subintervalo en una partición de$[a,b]$. Ahora vamos a$||\Delta x||$ representar la longitud del subintervalo más grande en la partición: es decir,$||\Delta x||$ es el más grande de todos los$\Delta x_i$ s. si$||\Delta x||$ es pequeño, entonces se$[a,b]$ debe dividir en muchos subintervalos, ya que todos los subintervalos deben tener longitudes pequeñas. “Tomar el límite como$||\Delta x||$ va a cero” implica que el número$n$ de subintervalos en la partición está creciendo hasta el infinito, ya que la mayor longitud del subintervalo se está volviendo arbitrariamente pequeña. Luego interpretamos la expresión

$$\ lim_ {||\ Delta x||\ a 0}\ suma_ {i=1} ^nf (c_i)\ Delta x_i\]

como “el límite de la suma de rectángulos, donde el ancho de cada rectángulo puede ser diferente pero cada vez más pequeño, y la altura de cada rectángulo no está necesariamente determinada por una regla en particular”. El teorema afirma que esta suma de Riemann también da el valor de la integral definida de$f$ más$[a,b]$.

Teorema$\PageIndex{2}$: Definite Integrals and the Limit of Riemann Sums

Dejar$f$ ser continuo en el intervalo cerrado$[a,b]$ y dejar$S_L(n)$,$S_R(n)$ y$S_M(n)$ ser definido como antes. Entonces:

1. $\lim_{n\to\infty} S_L(n) = \lim_{n\to\infty} S_R(n) = \lim_{n\to\infty} S_M(n) = \lim_{n\to\infty}\sum_{i=1}^n f(c_i)\Delta x$,
2. $\lim_{n\to\infty}\sum_{i=1}^n f(c_i)\Delta x = \int_a^b f(x)dx$, and %$ \lim_{n\to\infty} S_L(n) = \int_a^b f(x)dx$.
3. $\lim_{\|\Delta x\|\to 0} \sum_{i=1}^n f(c_i)\Delta x_i = \int_a^b f(x)dx$.

Resumimos aquí lo que hemos aprendido en las últimas secciones.

• Conocer el “área bajo la curva” puede ser útil. Un ejemplo común es: el área bajo una curva de velocidad es el desplazamiento.
• Hemos definido la integral definida,$\int_a^b f(x)dx$, para ser el área firmada bajo$f$ en el intervalo$[a,b]$.
• Si bien podemos aproximar una integral definida de muchas maneras, nos hemos centrado en usar rectángulos cuyas alturas se pueden determinar usando: la Regla de la Mano Izquierda, la Regla de la Mano Derecha y la Regla del Punto Medio.
• Las sumas de rectángulos de este tipo se llaman sumas de Riemann.
• El valor exacto de la integral definida se puede calcular usando el límite de una suma de Riemann. Generalmente usamos uno de los métodos anteriores ya que simplifica el álgebra.

Primero aprendimos de los derivados a través de los límites y luego aprendimos reglas que simplificaban el proceso. Conocemos una manera de evaluar una integral definida usando límites; en la siguiente sección veremos cómo el Teorema Fundamental del Cálculo simplifica el proceso. La característica clave de este teorema es su conexión entre la integral indefinida y la integral definida.

Colaboradores y Atribuciones

• Template:ContribApexCalc
• Template:ContribMarshall