7.3: El Método Shell

Última actualización
Guardar como PDF

Page ID: 111795

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

A menudo un problema determinado se puede resolver de más de una manera. Un método particular puede ser elegido por conveniencia, preferencia personal, o tal vez necesidad. En definitiva, es bueno tener opciones.

En la sección anterior se introdujeron los Métodos de Disco y Lavadora, que computaron el volumen de sólidos de revolución integrando el área transversal del sólido. En esta sección se desarrolla otro método de cálculo del volumen, el Método Shell. En lugar de cortar el sólido perpendicular al eje de rotación creando secciones transversales, ahora lo cortamos paralelo al eje de rotación, creando “conchas”.

Consideremos la Figura$\PageIndex{1}$, donde la región mostrada en (a) se gira alrededor del$y$ eje -formando el sólido mostrado en (b). Una pequeña porción de la región se dibuja en (a), paralela al eje de rotación. Cuando se gira la región, esta delgada rebanada forma una concha cilíndrica, como se muestra en la parte (c) de la figura. La sección anterior se aproximaba a un sólido con muchos discos delgados (o arandelas); ahora aproximamos a un sólido con muchas conchas cilíndricas delgadas.

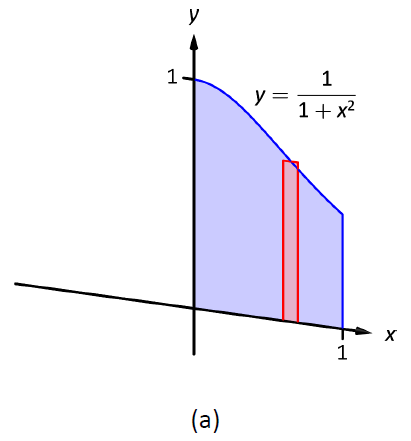
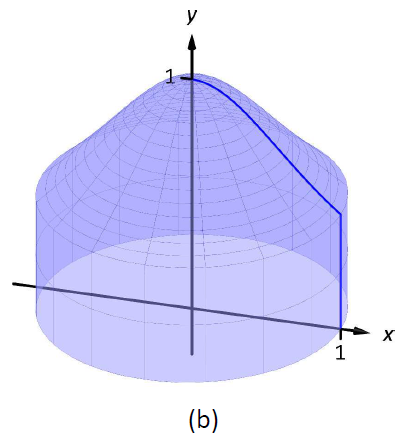
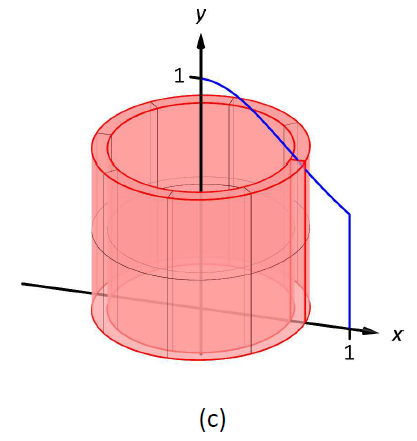
$7.3.1a.png$ $7.3.1b.png$ $7.3.1c.png$

Figura$\PageIndex{1}$: Introducción al Método Shell.

Figura$\PageIndex{1}$ (d): Una versión dinámica de esta figura creada usando CalcPlot3D.

Para calcular el volumen de una cáscara, primero considere la etiqueta de papel en una lata de sopa con radio$r$ y altura$h$. ¿Cuál es el área de esta etiqueta? Una forma sencilla de determinar esto es cortar la etiqueta y colocarla plana, formando un rectángulo con altura$h$ y longitud$2\pi r$. Así es el área$A = 2\pi rh$; ver Figura$\PageIndex{2a}$.

Haga un proceso similar con una carcasa cilíndrica, con altura$h$$\Delta x$, grosor y radio aproximado$r$. Cortar el caparazón y colocarlo plano forma un sólido rectangular con longitud$2\pi r$, altura$h$ y profundidad$dx$. Así es el volumen$V \approx 2\pi rh\ dx$; ver Figura$\PageIndex{2c}$. (Decimos “aproximadamente” ya que nuestro radio era una aproximación.)

Al romper el sólido en cáscaras$n$ cilíndricas, podemos aproximar el volumen del sólido como

$$V =\ suma_ {i=1} ^n 2\ pi r_ih_i\ dx_i,\]

donde$r_i$,$h_i$ y$dx_i$ son el radio, la altura y el grosor del$i\,^\text{th}$ caparazón, respectivamente.

Se trata de un Riemann Sum. Tomar un límite a medida que el grosor de los proyectiles se acerca a 0 conduce a una integral definida.

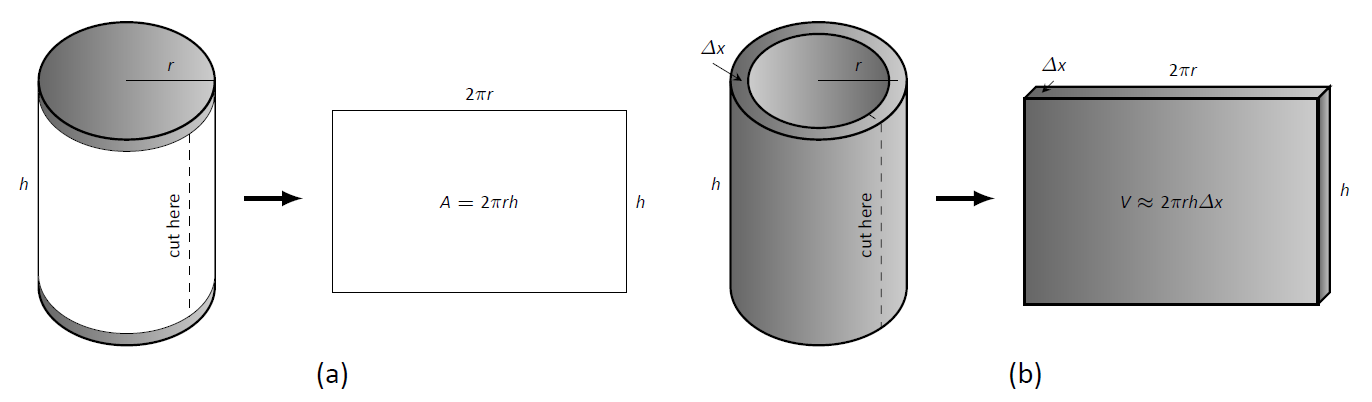
$7.3.2.png$

Figura$\PageIndex{2}$: Determinar el volumen de una concha cilíndrica delgada.} \ label {fig:soupcan}

Idea Clave 25: Método Shell

Dejar que se forme un sólido girando una región$R$, delimitada por$x=a$ y$x=b$, alrededor de un eje vertical. Let$r(x)$ representar la distancia desde el eje de rotación a$x$ (es decir, el radio de una cáscara de muestra) y dejar$h(x)$ representar la altura del sólido en$x$ (es decir, la altura de la cáscara). El volumen del sólido es

\[V = 2\pi\int_a^b r(x)h(x)\ dx.\]

Casos Especiales:

Cuando la región$R$ está delimitada arriba$y=f(x)$ y abajo por$y=g(x)$, entonces$h(x) = f(x)-g(x)$.
Cuando el eje de rotación es el$y$ -eje (i.e.,$x=0$) entonces$r(x) = x$.

Practicemos usando el Método Shell.

Ejemplo$\PageIndex{1}$: Finding volume using the Shell Method

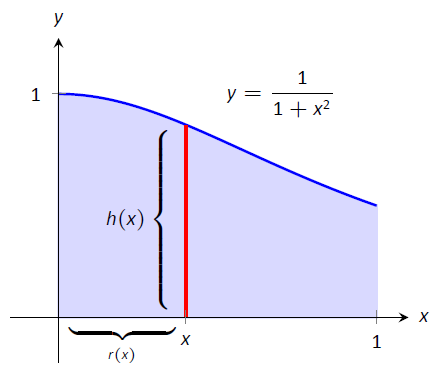
Encuentra el volumen del sólido formado al rotar la región delimitada por$y=0$$y=1/(1+x^2)$,$x=0$ y$x=1$ alrededor del$y$ eje.

Solución

Esta es la región utilizada para introducir el Método Shell en la Figura$\PageIndex{1}$, pero se esboza nuevamente en la Figura$\PageIndex{3}$ para una referencia más cercana. Se dibuja una línea en la región paralela al eje de rotación que representa un caparazón que se tallará a medida que la región se gira alrededor del$y$ eje -eje. (Este es el elemento diferencial.)

$7.3.3.png$

Figura$\PageIndex{3}$: Graficando una región en Ejemplo$\PageIndex{1}$.

La distancia que esta línea está desde el eje de rotación determina$r(x)$; como es la distancia desde$x$ el$y$ eje -eje$x$, tenemos$r(x)=x$. La altura de esta línea determina$h(x)$; la parte superior de la línea está en$y=1/(1+x^2)$, mientras que la parte inferior de la línea está en$y=0$. Así$h(x) = 1/(1+x^2)-0 = 1/(1+x^2)$. La región está delimitada de$x=0$ a$x=1$, por lo que el volumen es

\[V = 2\pi\int_0^1 \dfrac{x}{1+x^2}\ dx.\]

Esto requiere sustitución. Vamos$u=1+x^2$, entonces$du = 2x\ dx$. También cambiamos los límites:$u(0) = 1$ y$u(1) = 2$. Así tenemos:

\[\begin{align*} &= \pi\int_1^2 \dfrac{1}{u}\ du \\[4pt] &= \pi\ln u\Big|_1^2\\[4pt] &= \pi\ln 2 - \pi\ln 1\\[4pt] &= \pi\ln 2 \approx 2.178 \ \text{units}^3.\end{align*}\]

Nota: para poder encontrar este volumen usando el Método de Disco, se necesitarían dos integrales para dar cuenta de las regiones arriba y abajo$y=1/2$.

Con el Método Shell, no es necesario contabilizar nada especial para calcular el volumen de un sólido que tiene un agujero en el medio, como se demuestra a continuación.

Ejemplo$\PageIndex{2}$: Finding volume using the Shell Method

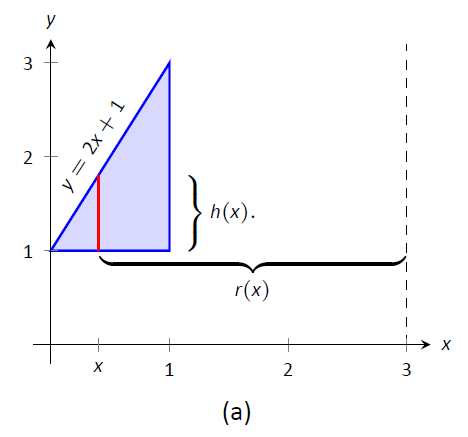
Encuentra el volumen del sólido formado girando la región triangular determinada por los puntos$(0,1)$,$(1,1)$ y$(1,3)$ alrededor de la línea$x=3$.

Solución

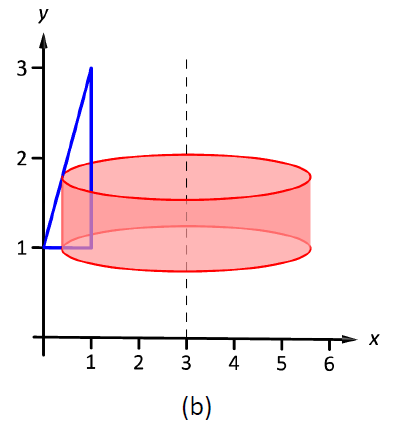
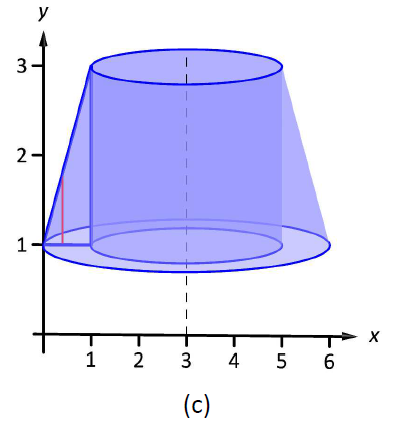
La región se esboza en la Figura$\PageIndex{4a}$ junto con el elemento diferencial, una línea dentro de la región paralela al eje de rotación. En la parte (b) de la figura, vemos la concha trazada por el elemento diferencial, y en la parte (c) se muestra todo el sólido.

$7.3.4a.png$ $7.3.4b.png$ $7.3.4c.png$

Figura$\PageIndex{4}$: Graficando una región en Ejemplo$\PageIndex{2}$

La altura del elemento diferencial es la distancia de$y=1$ a$y=2x+1$, la línea que conecta los puntos$(0,1)$ y$(1,3)$. Así$h(x) = 2x+1-1 = 2x$. El radio del caparazón formado por el elemento diferencial es la distancia de$x$ a$x=3$; es decir, lo es$r(x)=3-x$. Los$x$ límites de la región son$x=0$ a$x=1$, dando

\[\begin{align*} V &= 2\pi\int_0^1 (3-x)(2x)\ dx \\[4pt] &= 2\pi\int_0^1 \big(6x-2x^2)\ dx \\[4pt] &= 2\pi\left(3x^2-\dfrac23x^3\right)\Big|_0^1\\[4pt] &= \dfrac{14}{3}\pi\approx 14.66 \ \text{units}^3.\end{align*}\]

Al girar una región alrededor de un eje horizontal, debemos considerar las funciones de radio y altura en términos de$y$, no$x$.

Ejemplo$\PageIndex{3}$: Finding volume using the Shell Method

Encuentra el volumen del sólido formado por la rotación de la región dada en Ejemplo$\PageIndex{2}$ alrededor del$x$ eje -eje.

Solución

La región se esboza en la Figura$\PageIndex{5a}$ con un elemento diferencial de muestra. En la parte (b) de la figura se dibuja el caparazón formado por el elemento diferencial, y el sólido se esboza en (c). (Obsérvese que la región triangular se ve aquí “corta y ancha”, mientras que en el ejemplo anterior la misma región se veía “alta y estrecha”. Esto se debe a que los límites en las gráficas son diferentes.)

La altura del elemento diferencial es una$x$ -distancia, entre$x=\dfrac12y-\dfrac12$ y$x=1$. Así$h(y) = 1-(\dfrac12y-\dfrac12) = -\dfrac12y+\dfrac32.$ El radio es la distancia desde$y$ el$x$ eje -eje, entonces$r(y) =y$. Los$y$ límites de la región son$y=1$ y$y=3$, conduciendo a la integral

\[\begin{align*}V &= 2\pi\int_1^3\left[y\left(-\dfrac12y+\dfrac32\right)\right]\ dy \\[4pt]&= 2\pi\int_1^3\left[-\dfrac12y^2+\dfrac32y\right]\ dy \\[4pt] &= 2\pi\left[-\dfrac16y^3+\dfrac34y^2\right]\Big|_1^3 \\[4pt] &= 2\pi\left[\dfrac94-\dfrac7{12}\right]\\[4pt] &= \dfrac{10}{3}\pi \approx 10.472\ \text{units}^3.\end{align*}\]

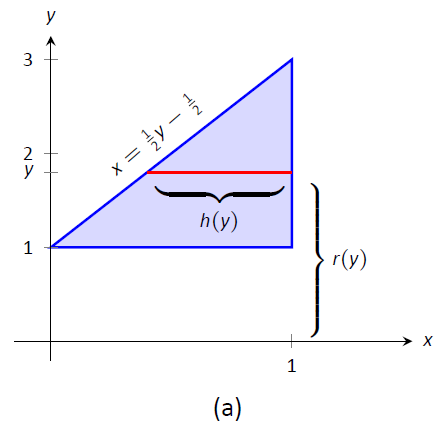
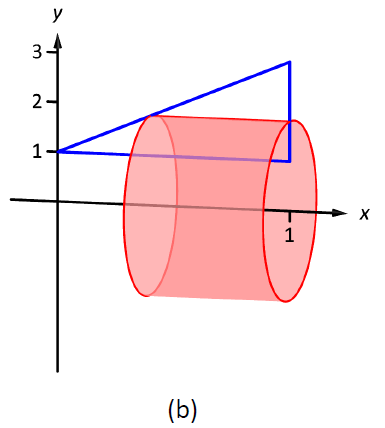
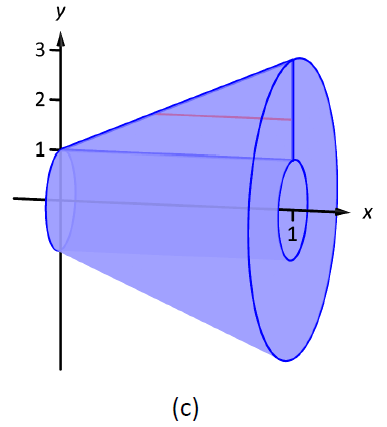
$7.3.5a.png$ $7.3.5b.png$ $7.3.5c.png$

Figura$\PageIndex{5}$: Graficando una región en Ejemplo$\PageIndex{3}$

Al inicio de esta sección se afirmó que “es bueno tener opciones”. El siguiente ejemplo encuentra el volumen de un sólido con bastante facilidad con el Método Shell, pero usar el Método Washer sería una gran tarea.

Ejemplo$\PageIndex{4}$: Finding volume using the Shell Method

Encuentra el volumen del sólido formado girando la región delimitada por$y= \sin x$ y el$x$ eje -desde$x=0$ hasta$x=\pi$ alrededor del$y$ eje -eje.

Solución

La región y un elemento diferencial, la cubierta formada por este elemento diferencial, y el sólido resultante se dan en la Figura$\PageIndex{6}$.

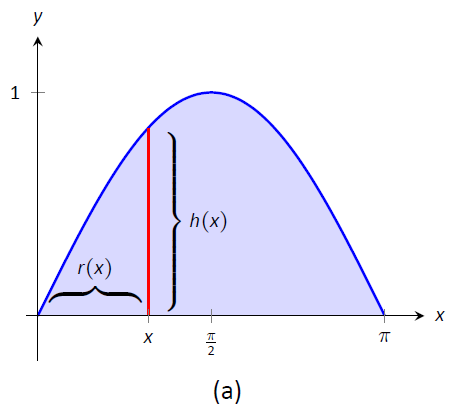
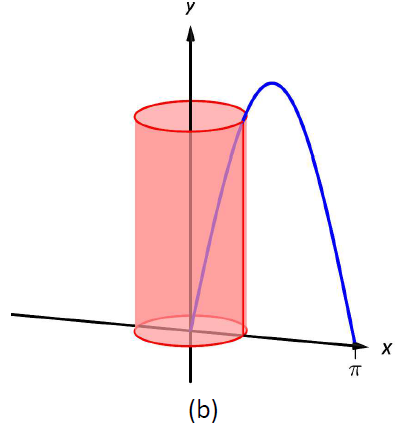
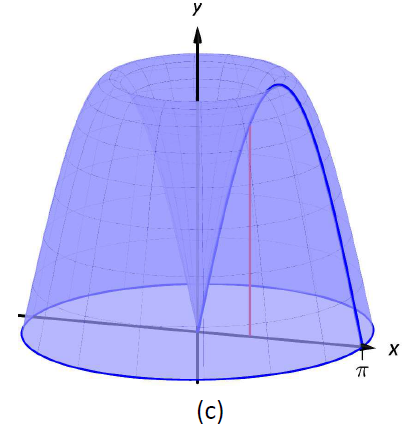
$7.3.6a.png$ $7.3.6b.png$ $7.3.6c.png$

Figura$\PageIndex{6}$: Graficando una región en Ejemplo$\PageIndex{4}$

El radio de una cáscara de muestra es$r(x) = x$; la altura de una cáscara de muestra es$h(x) = \sin x$, cada uno de$x=0$ a$x=\pi$. Así, el volumen del sólido es

\[V = 2\pi\int_0^{\pi} x\sin x\ dx.\]

Esto requiere Integración por Partes. Set$u=x$ y$dv=\sin x\ dx$; dejamos que el lector llene el resto. Contamos con:

\ [\ begin {align*} &= 2\ pi\ Grande [-x\ cos x\ Big|_0^ {\ pi} +\ int_0^ {\ pi}\ cos x\ dx\ Grande]\\ [4pt]
&= 2\ pi\ grande [\ pi +\ sin x\ Big|_0^ {\ pi}\\ grande]\\ [4pt]
&= 2\ pi\ Grande [\ pi + 0\ Grande]\\ [4pt]
&= 2\ pi^2\ aprox. 19.74\\ texto {unidades} ^3. \ end {alinear*}\]

Tenga en cuenta que para poder utilizar el Método de Arandela, necesitaríamos resolver$y=\sin x$ para$x$, requiriendo el uso de la función arcsine. Dejamos al lector verificar que la función de radio exterior es$R(y) = \pi-\arcsin y$ y la función de radio interior lo es$r(y)=\arcsin y$. Así, el volumen puede calcularse como

$$\ pi\ int_0^1\ Grande [(\ pi-\ arcsin y) ^2- (\ arcsin y) ^2\ Grande]\ dy.\]

Esta integral no es terrible dado que los$\arcsin^2 y$ términos cancelan, pero es más onerosa que la integral creada por el Método Shell.

Terminamos esta sección con una tabla que resume el uso de los Métodos de Arandela y Shell.

Idea Clave 26: Resumen de los Métodos de Arandela y Carcasa

Que$R$ se dé una región con$x$ -límites$x=a$ y$x=b$ y$y$ -límites$y=c$ y$y=d$.

\[\begin{align*} & \text{Washer Method} & & \text{Shell Method} \\[4pt] \text{Horizontal Axis} \quad & \pi\int_a^b \big(R(x)^2-r(x)^2\big)\ dx & & 2\pi\int_c^d r(y)h(y)\ dy \\[4pt] \\[4pt] \text{Vertical Axis} \quad & \pi \int_c^d\big(R(y)^2-r(y)^2\big)\ dy & & 2\pi\int_a^b r(x)h(x)\ dx \end{align*}\]

Al igual que en el apartado anterior, el objetivo real de esta sección no es poder computar volúmenes de ciertos sólidos. Más bien, es poder resolver un problema aproximando primero, luego usando límites para afinar la aproximación para dar el valor exacto. En esta sección, aproximamos el volumen de un sólido cortándolo en conchas cilíndricas delgadas. Al resumir los volúmenes de cada shell, obtenemos una aproximación del volumen. Al tomar un límite a medida que el número de conchas igualmente espaciadas va al infinito, nuestra suma puede ser evaluada como una integral definida, dando el valor exacto.

Utilizamos este mismo principio nuevamente en la siguiente sección, donde encontramos la longitud de las curvas en el plano.