8.3: Pruebas integrales y de comparación

Saber si una serie converge o no es muy importante, especialmente cuando hablamos de la serie Power. Los teoremas 60 y 61 dan criterios para cuando convergen Geométrico y\(p\) -series, y el Teorema 63 da una prueba rápida para determinar si una serie diverge. Hay muchas series importantes cuya convergencia no puede ser determinada por estos teoremas, sin embargo, por lo que introducimos un conjunto de pruebas que nos permiten manejar una amplia gama de series. Comenzamos con la Prueba Integral.

Prueba Integral

Afirmamos en la Sección 8.1 que una secuencia\(\{a_n\}\) es una función\(a(n)\) cuyo dominio es\(\mathbb{N}\), el conjunto de números naturales. Si podemos extender\(a(n)\) a\(\mathbb{R}\), los números reales, y es tanto positivo como decreciente en\([1,\infty)\), entonces la convergencia de\( \sum\limits_{n=1}^\infty a_n\) es la misma que\(\int\limits_1^\infty a(x)dx\).

teorema\(\PageIndex{1}\): integral test

Dejar que una secuencia\(\{a_n\}\) se defina por\(a_n=a(n)\), donde\(a(n)\) es continua, positiva y decreciente en\([1,\infty)\). Entonces\( \sum\limits_{n=1}^\infty a_n\) converge, si, y sólo si,\(\int\limits_1^\infty a(x) dx\) converge.

Podemos demostrar la verdad de la Prueba Integral con dos gráficas simples. En la Figura\(\PageIndex{1a}\), la altura de cada rectángulo es\(a(n)=a_n\) para\(n=1,2,\ldots\), y claramente los rectángulos encierran más área que el área debajo\(y=a(x)\). Por lo tanto podemos concluir que

\[\int\limits_1^\infty a(x) dx < \sum\limits_{n=1}^\infty a_n.\label{eq:integral_testa}\]

Figura\(\PageIndex{1}\): Ilustrando la verdad de la Prueba Integral.

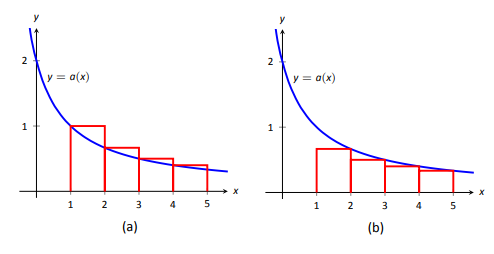
En Figura\(\PageIndex{1b}\), dibujamos rectángulos debajo\(y=a(x)\) con la regla de la Mano Derecha, comenzando con\(n=2\). Esta vez, el área de los rectángulos es menor que el área debajo\(y=a(x)\), entonces\(\sum\limits_{n=2}^\infty a_n < \int\limits_1^\infty a(x) dx\). Observe cómo comienza esta suma\(n=2\);\(a_1\) sumar a ambos lados nos permite reescribir la suma comenzando con\(n=1\):

\[\sum\limits_{n=1}^\infty a_n < a_1 +\int\limits_1^\infty a(x) dx.\label{eq:integral_testb}\]

Combinando Ecuaciones\ ref {eq:integral_testa} y\ ref {eq:integral_testb}, tenemos

\[\sum\limits_{n=1}^\infty a_n< a_1 +\int\limits_1^\infty a(x) dx < a_1 + \sum\limits_{n=1}^\infty a_n.\label{eq:integral_testc}\]

Teorema\(\PageIndex{1}\)

A partir de la ecuación\ ref {eq:integral_testc} podemos hacer las siguientes dos declaraciones:

1. Si\( \sum\limits_{n=1}^\infty a_n\) diverge, también lo hace\(\int\limits_1^\infty a(x) dx\) (porque\( \sum\limits_{n=1}^\infty a_n < a_1 +\int\limits_1^\infty a(x) dx)\)
2. Si\( \sum\limits_{n=1}^\infty a_n\) converge, también lo hace\(\int\limits_1^\infty a(x) dx\) (porque\( \int\limits_1^\infty a(x) dx < \sum\limits_{n=1}^\infty a_n.)\)

Por lo tanto, la serie y la integral o ambas convergen o ambas divergen.

El teorema nos\(\PageIndex{1}\) permite extender este teorema a series donde\(a(n)\) es positivo y decreciente\([b,\infty)\) para algunos\(b>1\).

Ejemplo\(\PageIndex{1}\): Using the Integral Test

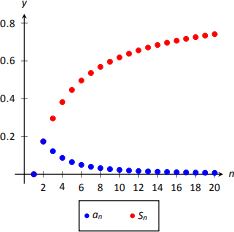
Determinar la convergencia de\(\sum\limits_{n=1}^\infty \dfrac{\ln n}{n^2}\). (Los términos de la secuencia\(\{a_n\} = \{\ln n/n^2\}\) y las n sumas\(^{\text{th}}\) parciales se dan en la Figura\(\PageIndex{2}\)).

Solución

La cifra\(\PageIndex{2}\) implica que\(a(n) = (\ln n)/n^2\) es positiva y decreciente en\([2,\infty)\). Esto también lo podemos determinar analíticamente. Sabemos que\(a(n)\) es positivo como ambos\(\ln n\) y lo\(n^2\) estamos en\([2,\infty)\). Para determinar que\(a(n)\) es decreciente, considere\(a^\prime(n) = (1-2\ln n)/n^3\), que es negativo para\(n\geq 2\). Ya que\(a^\prime(n)\) es negativo,\(a(n)\) es decreciente.

Figura\(\PageIndex{2}\): Trazando la secuencia y serie en Ejemplo\(\PageIndex{1}\).

Aplicando la Prueba Integral, probamos la convergencia de\( \int\limits_1^\infty \dfrac{\ln x}{x^2} dx\). Integrar esta integral inadecuada requiere el uso de Integración por Partes, con\(u = \ln x\) y\(dv = 1/x^2 dx\).

\[\begin{align*}\int\limits_1^\infty \dfrac{\ln x}{x^2} dx &=\lim\limits_{b\to\infty} \int\limits_1^b \dfrac{\ln x}{x^2} dx\\ &=\lim\limits_{b\to\infty} -\dfrac1x\ln x\Big|_1^b + \int\limits_1^b\dfrac1{x^2} dx \\ &=\lim\limits_{b\to\infty} -\dfrac1x\ln x -\dfrac 1x\Big|_1^b\\ &=\lim\limits_{b\to\infty}1-\dfrac1b-\dfrac{\ln b}{b}.\quad \text{Apply L'H\(\hat o\)pital's Rule:}\\ &= 1. \end{align*}\]

Ya que\( \int\limits_1^\infty \dfrac{\ln x}{x^2} dx\) converge, también lo hace\( \sum\limits_{n=1}^\infty \dfrac{\ln n}{n^2}\).

El teorema 61 se dio sin justificación, afirmando que la\(p\) serie general\( \sum\limits_{n=1}^\infty \dfrac 1{(an+b)^p}\) converge si, y sólo si,\(p>1\). En el siguiente ejemplo, demostramos que esto es cierto aplicando la Prueba Integral.

Ejemplo\(\PageIndex{2}\): Using the Integral Test to establish Theorem 61

Utilice la Prueba Integral para demostrar que\( \sum\limits_{n=1}^\infty \dfrac1{(an+b)^p}\) converge si, y solo si,\(p>1\).

Solución

Considerar la integral\(\int\limits_1^\infty \dfrac1{(ax+b)^p} dx\); asumiendo\(p\neq 1\),

\ [\ begin {alinear*}
\ int\ limits_1^\ infty\ dfrac1 {(ax+b) ^p} dx &=\ lim\ limits_ {c\ a\ infty}\ int\ limits_1^c\ dfrac1 {(ax+b) ^p} dx\\
&=\ lim\ límites_ {c\ a\ infty}\ dfrac {} {a (1-p)} (ax+b) ^ {1-p}\ big|_1^C\\
&=\ lim\ límites_ {c\ a\ infty}\ dfrac {1} {a (1-p)}\ grande ((ac+b) ^ {1-p} - ( a+b) ^ {1-p}\ grande).
\ end {alinear*}\]

Este límite converge si, y sólo si,\(p>1\). Es fácil demostrar que la integral también diverge en el caso de\(p=1\). (Este resultado es similar al trabajo anterior a Key Idea 21.)

Por lo tanto\( \sum\limits_{n=1}^\infty \dfrac 1{(an+b)^p}\) converge si, y sólo si,\(p>1\).

Consideramos dos pruebas de convergencia más en esta sección, ambas pruebas de comparación. Es decir, determinamos la convergencia de una serie comparándola con otra serie con convergencia conocida.

Prueba de comparación directa

teorema\(\PageIndex{1}\): direct comparison test

Dejar\(\{a_n\}\) y\(\{b_n\}\) ser secuencias positivas donde\(a_n\leq b_n\) para todos\(n\geq N\), para algunos\(N\geq 1\).

1. Si\( \sum\limits_{n=1}^\infty b_n\) converge, entonces\( \sum\limits_{n=1}^\infty a_n\) converge.
2. Si\( \sum\limits_{n=1}^\infty a_n\) diverge, entonces\( \sum\limits_{n=1}^\infty b_n\) diverge.

Nota: Una secuencia\(\{a_n\}\) es una secuencia positiva si es\(a_n>0\) para todos\(n\).

Debido al Teorema 64, cualquier teorema que se base en una secuencia positiva sigue siendo cierto cuando\(a_n>0\) para todos menos un número finito de valores de\(n\).

Ejemplo\(\PageIndex{3}\): Applying the Direct Comparison Test

Determinar la convergencia de\(\sum\limits_{n=1}^\infty \dfrac1{3^n+n^2}\).

Solución

Esta serie no es ni geométrica ni\(p\) -serie, sino que parece relacionada. Predecimos que convergerá, así que buscamos una serie con términos más grandes que converja. (Tenga en cuenta también que la Prueba Integral parece difícil de aplicar aquí.)

Ya que\(3^n < 3^n+n^2\),\( \dfrac1{3^n}> \dfrac1{3^n+n^2}\) para todos\(n\geq1\). La serie\(\sum\limits_{n=1}^\infty \dfrac{1}{3^n}\) es una serie geométrica convergente; por Teorema 66,\( \sum\limits_{n=1}^\infty \dfrac1{3^n+n^2}\) converge.

Ejemplo\(\PageIndex{4}\): Applying the Direct Comparison Test

Determinar la convergencia de\(\sum\limits_{n=1}^\infty \dfrac{1}{n-\ln n}\).

Solución

Sabemos que la Serie Armónica\(\sum\limits_{n=1}^\infty \dfrac1n\) diverge, y parece que la serie dada está estrechamente relacionada con ella, de ahí que predecimos que divergirá.

Ya que\(n\geq n-\ln n\) para todos\(n\geq 1\),\( \dfrac1n \leq \dfrac1{n-\ln n}\) para todos\(n\geq 1\).

La Serie Armónica diverge, por lo que concluimos que también\(\sum\limits_{n=1}^\infty \dfrac{1}{n-\ln n}\) diverge.

El concepto de comparación directa es potente y a menudo relativamente fácil de aplicar. La práctica ayuda a desarrollar la intuición necesaria para elegir rápidamente una serie adecuada con la que comparar. Sin embargo, es fácil construir una serie para la que es difícil aplicar la Prueba de Comparación Directa.

Considerar\(\sum\limits_{n=1}^\infty \dfrac1{n+\ln n}\). Es muy similar a las series divergentes dadas en el Ejemplo 8.3.5. Sospechamos que también diverge, como\( \dfrac 1n \approx \dfrac1{n+\ln n}\) para grandes\(n\). No obstante, la desigualdad que naturalmente queremos utilizar “va por el camino equivocado”: ya que\(n\leq n+\ln n\) para todos\(n\geq 1\),\(\dfrac1n \geq \dfrac{1}{n+\ln n}\) para todos\(n\geq 1\). La serie dada tiene términos menores que los términos de una serie divergente, y no podemos concluir nada de esto.

Afortunadamente, podemos aplicar otra prueba a la serie dada para determinar su convergencia.

Prueba de comparación de límites grandes

Teorema 67: prueba de comparación de límites

Dejar\(\{a_n\}\) y\(\{b_n\}\) ser secuencias positivas.

1. Si\(\lim_{n\to\infty} \dfrac{a_n}{b_n} = L\), donde\(L\) es un número real positivo, entonces\( \sum\limits_{n=1}^\infty a_n\) y\( \sum\limits_{n=1}^\infty b_n\) o ambos convergen o ambos divergen.
2. Si\(\lim_{n\to\infty} \dfrac{a_n}{b_n} = 0\), entonces si\( \sum\limits_{n=1}^\infty b_n\) converge, entonces también lo hace\( \sum\limits_{n=1}^\infty a_n\).
3. Si\(\lim_{n\to\infty} \dfrac{a_n}{b_n} = \infty\), entonces si\( \sum\limits_{n=1}^\infty b_n\) diverge, entonces también lo hace\( \sum\limits_{n=1}^\infty a_n\).

El teorema 67 es más útil cuando\(\{b_n\}\) se conoce la convergencia de la serie de y estamos tratando de determinar la convergencia de la serie a partir de\(\{a_n\}\).

Utilizamos la prueba de comparación de límites en el siguiente ejemplo para examinar las series\(\sum\limits_{n=1}^\infty \dfrac1{n+\ln n}\) que motivaron esta nueva prueba.

Ejemplo\(\PageIndex{5}\): Applying the Limit Comparison Test

Determinar la convergencia del\(\sum\limits_{n=1}^\infty \dfrac1{n+\ln n}\) uso de la Prueba de Comparación de Límite.

Solución

Comparamos los términos de\(\sum\limits_{n=1}^\infty \dfrac1{n+\ln n}\) con los términos de la Secuencia Armónica\(\sum\limits_{n=1}^\infty \dfrac1{n}\):

\ [\ begin {align*}
\ lim_ {n\ a\ infty}\ dfrac {1/ (n+\ ln n)} {1/n} &=\ lim\ limits_ {n\ a\ infty}\ dfrac {n} {n+\ ln n}\\
&= 1\ quad\ text {(después de aplicar la Regla de L'H\(\hat o\) pital)}.
\ end {alinear*}\]

Dado que la Serie Armónica diverge, concluimos que también\(\sum\limits_{n=1}^\infty \dfrac1{n+\ln n}\) diverge.

Ejemplo\(\PageIndex{6}\): Applying the Limit Comparison Test

Determinar la convergencia de\(\sum\limits_{n=1}^\infty \dfrac1{3^n-n^2}\)

Solución
Esta serie es similar a la del Ejemplo 8.3.3, pero ahora estamos considerando ""\(3^n-n^2\) en lugar de "”\(3^n+n^2\).” Esta diferencia dificulta la aplicación de la Prueba de Comparación Directa.

En su lugar, utilizamos la prueba de comparación de límites y comparamos con la serie\(\sum\limits_{n=1}^\infty \dfrac1{3^n}\):

\ [\ begin {alinear*}
\ lim_ {n\ a\ infty}\ dfrac {1/ (3^n-n^2)} {1/3^n} &=\ lim\ limits_ {n\ a\ infty}\ dfrac {3^n} {3^n-n^2}\\
&= 1\ quad\ text {(después de aplicar la Regla de L'H\(\hat o\) pital dos veces)}.
\ end {alinear*}\]

Sabemos que\(\sum\limits_{n=1}^\infty \dfrac1{3^n}\) es una serie geométrica convergente, por lo tanto\(\sum\limits_{n=1}^\infty \dfrac1{3^n-n^2}\) converge también.

Como se mencionó anteriormente, la práctica ayuda a desarrollar la intuición para elegir rápidamente una serie con la que comparar. Una regla general es elegir una serie basada en el término dominante en la expresión de\(\{a_n\}\). También es útil señalar que los factoriales dominan exponenciales, que dominan las funciones algebraicas (e.g., polinomios), que dominan logaritmos. En el ejemplo anterior, el término dominante de\(\dfrac{1}{3^n-n^2}\) era\(3^n\), así que comparamos la serie con\( \sum\limits_{n=1}^\infty \dfrac1{3^n}\). Sin embargo, es difícil aplicar la Prueba de Comparación de Límites a series que contienen factoriales, ya que no hemos aprendido a aplicar la Regla de L'H\(\hat o\) pital a\(n!\).

Ejemplo\(\PageIndex{7}\): Applying the Limit Comparison Test

Determinar la convergencia de\(\sum\limits_{n=1}^\infty \dfrac{\sqrt{n}+3}{n^2-n+1}\).

Solución

Ingenuamente intentamos aplicar la regla general dada anteriormente y notamos que el término dominante en la expresión de la serie es\(1/n^2\). Sabiendo que\( \sum\limits_{n=1}^\infty \dfrac1{n^2}\) converge, intentamos aplicar la Prueba de Comparación de Límite:

\ [\ begin {alinear*}
\ lim_ {n\ a\ infty}\ dfrac {(\ sqrt {n} +3)/(n^2-n+1)} {1/n^2} &=\ lim\ límites_ {n\ a\ infty}\ dfrac {n^2 (\ sqrt n+3)} {n^2-n+1}\
&=\ infty\ quad\ text {(Aplica la Regla de L'H\(\hat o\) pital)}.
\ end {alinear*}\]

Teorema 67 parte (3) sólo se aplica cuando\(\sum\limits_{n=1}^\infty b_n\) diverge; en nuestro caso, converge. En definitiva, nuestra prueba no ha revelado nada sobre la convergencia de nuestra serie.

El problema es que elegimos una serie pobre con la que comparar. Dado que el numerador y el denominador de los términos de la serie son funciones algebraicas, deberíamos haber comparado nuestra serie con el término dominante del numerador dividido por el término dominante del denominador.

El término dominante del numerador es\(n^{1/2}\) y el término dominante del denominador es\(n^2\). Por lo tanto, debemos comparar los términos de la serie dada con\(n^{1/2}/n^2 = 1/n^{3/2}\):

\ [\ begin {align*}
\ lim_ {n\ a\ infty}\ dfrac {(\ sqrt {n} +3)/(n^2-n+1)} {1/n^ {3/2}} &=\ lim\ limits_ {n\ a\ infty}\ dfrac {n^ {3/2} (\ sqrt n+3)} {n^2-n+1}\\
&= 1\ quad\ text {(Aplica la Regla de L'H\(\hat o\) pital)}.
\ end {alinear*}\]

Dado que la\(p\) serie\(\sum\limits_{n=1}^\infty \dfrac1{n^{3/2}}\) -converge, concluimos que también\(\sum\limits_{n=1}^\infty \dfrac{\sqrt{n}+3}{n^2-n+1}\) converge.

Mencionamos anteriormente que la Prueba Integral no funcionó bien con series que contenían términos factoriales. En la siguiente sección se presenta la Prueba de Relación, que maneja bien dichas series. También presentamos la Prueba Raíz, que es buena para series donde cada término se eleva a una potencia.

Colaboradores y Atribuciones

• Template:ContribApexCalc