9.3: La divergencia y las pruebas integrales

Última actualización
Guardar como PDF

Page ID: 116568

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Utilice la prueba de divergencia para determinar si una serie converge o diverge.
Utilice la prueba integral para determinar la convergencia de una serie.
Estimar el valor de una serie encontrando límites en su término restante.

En el apartado anterior, determinamos la convergencia o divergencia de varias series calculando explícitamente el límite de la secuencia de sumas parciales\( {S_k}.\) En la práctica, calcular explícitamente este límite puede ser difícil o imposible. Por suerte, existen varias pruebas que nos permiten determinar la convergencia o divergencia para muchos tipos de series. En esta sección, se discuten dos de estas pruebas: la prueba de divergencia y la prueba integral. Examinaremos varias otras pruebas en el resto de este capítulo y luego resumiremos cómo y cuándo usarlas.

Prueba de divergencia

Para\(\displaystyle \sum^∞_{n=1}a_n\) que una serie converja, el\( n^{th}\) término\( a_n\) debe satisfacer\( a_n→0\) como\( n→∞.\) Por lo tanto, a partir de las propiedades límite algebraicas de las secuencias,

\[\begin{align*} \lim_{k→∞}a_k = \lim_{k→∞}(S_k−S_{k−1}) \\[4pt] =\lim_{k→∞}S_k−\lim_{k→∞}S_{k−1} \\[4pt] =S−S=0. \end{align*}\]

Por lo tanto, si\(\displaystyle \sum_{n=1}^∞a_n\) converge, el\( n^{th}\) término\( a_n→0\) como\( n→∞.\) Una consecuencia importante de este hecho es la siguiente afirmación:

Si\( a_n↛0\) como\(\displaystyle n→∞,\sum_{n=1}^∞a_n\) diverge.

Esta prueba se conoce como la prueba de divergencia porque proporciona una forma de demostrar que una serie diverge.

Definición: La prueba de divergencia

Si existe\(\displaystyle \lim_{n→∞}a_n=c≠0\) o\(\displaystyle \lim_{n→∞}a_n\) no, entonces la serie\(\displaystyle \sum_{n=1}^∞a_n\) diverge.

Es importante señalar que lo contrario de este teorema no es cierto. Es decir, si\(\displaystyle \lim_{n→∞}a_n=0\), no podemos llegar a ninguna conclusión sobre la convergencia de\(\displaystyle \sum_{n=1}^∞a_n\).

Por ejemplo,\(\displaystyle \lim_{n→0}\tfrac{1}{n}=0\), pero la serie armónica\(\displaystyle \sum^∞_{n=1}\frac{1}{n}\) diverge. En esta sección y en las secciones restantes de este capítulo, mostramos muchos más ejemplos de este tipo de series. En consecuencia, aunque podemos usar la prueba de divergencia para demostrar que una serie diverge, no podemos usarla para probar que una serie converge. Específicamente, si\( a_n→0\), la prueba de divergencia no es concluyente.

Ejemplo\( \PageIndex{1}\): Using the divergence test

Para cada una de las siguientes series, aplicar la prueba de divergencia. Si la prueba de divergencia prueba que la serie diverge, indíquelo así. De lo contrario, indicar que la prueba de divergencia no es concluyente.

\(\displaystyle \sum^∞_{n=1}\frac{n}{3n−1}\)
\(\displaystyle \sum^∞_{n=1}\frac{1}{n^3}\)
\(\displaystyle \sum^∞_{n=1}e^{1/n^2}\)

Solución

Ya que\(\displaystyle \lim_{n→∞} \frac{n}{3n−1}=\frac{1}{3}≠0\), por la prueba de divergencia, podemos concluir que\(\displaystyle \sum_{n=1}^∞\dfrac{n}{3n−1}\) diverge.
Ya que\(\displaystyle \lim_{n→∞} \frac{1}{n^3}=0\), la prueba de divergencia no es concluyente.
Ya que\(\displaystyle \lim_{n→∞} e^{1/n^2}=1≠0\), por la prueba de divergencia, la serie\(\displaystyle \sum_{n=1}^∞e^{1/n^2}\) diverge.

Ejercicio\( \PageIndex{1}\)

¿Qué nos dice la prueba de divergencia sobre la serie\(\displaystyle \sum_{n=1}^∞\cos(1/n^2)\)?

Pista: Mira\(\displaystyle \lim_{n→∞}\cos(1/n^2)\).
Contestar: La serie diverge.

Prueba Integral

En la sección anterior, probamos que la serie armónica diverge al observar la secuencia de sumas parciales\( {S_k}\) y mostrarla\( S_{2^k}>1+k/2\) para todos los enteros positivos\( k\). En esta sección utilizamos una técnica diferente para probar la divergencia de las series armónicas. Esta técnica es importante porque se utiliza para probar la divergencia o convergencia de muchas otras series. Esta prueba, llamada prueba integral, compara una suma infinita con una integral impropia. Es importante señalar que esta prueba sólo se puede aplicar cuando estamos considerando una serie cuyos términos son todos positivos.

Esta es una gráfica en el cuadrante 1 de una curva descendente cóncava hacia arriba que se aproxima al eje x — f (x) = 1/x Se dibujan cinco rectángulos con base 1 sobre el intervalo [1, 6]. La altura de cada rectángulo está determinada por el valor de la función en el punto final izquierdo de la base del rectángulo. Las áreas para cada una están marcadas: 1, 1/2, 1/3, 1/4 y 1/5. — Figura\(\PageIndex{1}\) : La suma de las áreas de los rectángulos es mayor que el área entre la curva\( f(x)=1/x\) y el\( x\) eje para\( x≥1\). Dado que el área delimitada por la curva es infinita (calculada por una integral impropia), la suma de las áreas de los rectángulos también es infinita.

Para ilustrar cómo funciona la prueba integral, use como ejemplo la serie armónica. En Figura\(\PageIndex{1}\), representamos la serie armónica dibujando una secuencia de rectángulos con áreas\( 1,1/2,1/3,1/4,…\) junto con la función\( f(x)=1/x.\) A partir de la gráfica, vemos que

\[\sum_{n=1}^k\dfrac{1}{n}=1+\dfrac{1}{2}+\dfrac{1}{3}+⋯+\dfrac{1}{k}>∫^{k+1}_1\dfrac{1}{x}\,dx. \nonumber \]

Por lo tanto, para cada uno\( k\), la suma\( k^{\text{th}}\) parcial\( S_k\) satisface

\[\begin{align*} S_k =\sum_{n=1}^k\dfrac{1}{n} >∫^{k+1}_1\dfrac{1}{x}\,dx = \ln x \big| ^{k+1}_1 \\[4pt] = \ln (k+1)−\ln (1) \\[4pt] =\ln (k+1).\end{align*}\]

Ya que\(\displaystyle \lim_{k→∞}\ln(k+1)=∞,\) vemos que la secuencia de sumas parciales no\( {S_k}\) tiene límites. Por lo tanto,\( {S_k}\) diverge, y, en consecuencia, la serie\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n}\) también diverge.

Esta es una gráfica en el cuadrante 1 de la curva ascendente cóncava decreciente f (x) = 1/ (x^2), que se acerca al eje x. Los rectángulos de la base 1 se dibujan sobre el intervalo [0, 5]. La altura de cada rectángulo está determinada por el valor de la función en el punto final derecho de su base. Las áreas de cada una están marcadas: 1, 1/ (2^2), 1/ (3^2), 1/ (4^2) y 1/ (5^2). — Figura\(\PageIndex{2}\): La suma de las áreas de los rectángulos es menor que la suma del área del primer rectángulo y el área entre la curva\( f(x)=1/x^2\) y el\( x\) eje para\( x≥1\). Dado que el área delimitada por la curva es finita, la suma de las áreas de los rectángulos también es finita.

Ahora considera la serie\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\). Mostramos cómo se puede utilizar una integral para demostrar que esta serie converge. En la Figura\(\PageIndex{2}\), se esboza una secuencia de rectángulos con áreas\( 1,1/2^2,1/3^2,…\) junto con la función\( f(x)=\frac{1}{x^2}\). De la gráfica vemos que

\[\sum_{n=1}^k\dfrac{1}{n^2}=1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+⋯+\dfrac{1}{k^2}<1+∫^k_1\dfrac{1}{x^2}\,dx. \nonumber \]

Por lo tanto, para cada uno\( k\), la suma\( k^{\text{th}}\) parcial\( S_k\) satisface

\[\begin{align*} S_k=\sum_{n=1}^k\dfrac{1}{n^2}<1+∫^k_1\dfrac{1}{x^2}\,dx =1−\left. \dfrac{1}{x} \right|^k_1 \\[4pt] =1−\dfrac{1}{k}+1 \\[4pt] =2−\dfrac{1}{k}<2. \end{align*}\]

Se concluye que la secuencia de sumas parciales\( {S_k}\) está delimitada. También vemos que\( {S_k}\) es una secuencia creciente:

\[S_k=S_{k−1}+\dfrac{1}{k^2} \nonumber \]

para\( k≥2\).

Ya que\( {S_k}\) es creciente y acotado, por el Teorema de Convergencia Monótona, converge. Por lo tanto, la serie\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\) converge.

Esto muestra dos gráficas lado a lado de la misma función y = f (x), una curva descendente cóncava hacia arriba que se aproxima al eje x. Los rectángulos se dibujan con base 1 a lo largo de los intervalos [0, 6] y [1, 6]. Para la gráfica de la izquierda, la altura de cada rectángulo está determinada por el valor de la función en el punto final derecho de su base. Para la gráfica de la derecha, la altura de cada rectángulo está determinada por el valor de la función en el punto final izquierdo de su base. Las áreas a_1 a a_6 están marcadas en la gráfica de la izquierda, y las mismas para a_1 a a_5 a la derecha. — Figura\(\PageIndex{3}\): (a) Si podemos inscribir rectángulos dentro de una región delimitada por una curva\( y=f(x)\) y el\( x\) eje -y el área delimitada por esas curvas para\( x≥1\) es finita, entonces la suma de las áreas de los rectángulos también es finita. (b) Si un conjunto de rectángulos circunscribe la región delimitada por\( y=f(x)\) y el\( x\) eje para\( x≥1\) y la región tiene área infinita, entonces la suma de las áreas de los rectángulos también es infinita.

Podemos extender esta idea para demostrar convergencia o divergencia para muchas series diferentes. Supongamos que\(\displaystyle \sum^∞_{n=1}a_n\) es una serie con términos positivos\( a_n\) tales que existe una función continua, positiva, decreciente\( f\) donde\( f(n)=a_n\) para todos los enteros positivos. Entonces, como en la Figura\(\PageIndex{3a}\), para cualquier entero\( k\), la suma\( k^{\text{th}}\) parcial\( S_k\) satisface

\[S_k=a_1+a_2+a_3+⋯+a_k<a_1+∫^k_1f(x)\,dx<1+∫^∞_1f(x)\,dx. \nonumber \]

Por lo tanto, si\(\displaystyle ∫^∞_1f(x)\,dx\) converge, entonces\( {S_k}\) se delimita la secuencia de sumas parciales. Ya que\( {S_k}\) es una secuencia creciente, si también es una secuencia acotada, entonces por el Teorema de Convergencia Monótona, converge. Concluimos que si\(\displaystyle ∫^∞_1f(x)\,dx\) converge, entonces la serie\(\displaystyle \sum^∞_{n=1}a_n\) también converge. Por otro lado, a partir de la Figura\(\PageIndex{3b}\), para cualquier entero\( k\), la suma\( k^{\text{th}}\) parcial\( S_k\) satisface

\[S_k=a_1+a_2+a_3+⋯+a_k>∫^{k+1}_1f(x)\,dx. \nonumber \]

\[ \lim_{k→∞}∫^{k+1}_1f(x)\,dx=∞, \nonumber \]

entonces\( {S_k}\) es una secuencia no acotada y por lo tanto diverge. Como resultado, la serie\(\displaystyle \sum_{n=1}^∞a_n\) también diverge. Dado que\( f\) es una función positiva, si\(\displaystyle ∫^∞_1f(x)\,dx\) diverge, entonces

\[ \lim_{k→∞}∫^{k+1}_1f(x)\,dx=∞. \nonumber \]

Concluimos que si\(\displaystyle ∫^∞_1f(x)\,dx\) diverge, entonces\(\displaystyle \sum_{n=1}^∞a_n\) diverge.

Definición: La prueba integral

Supongamos que\(\displaystyle \sum_{n=1}^∞a_n\) es una serie con términos positivos\( a_n\). Supongamos que existe una función\( f\) y un entero positivo\( N\) tal que se cumplen las siguientes tres condiciones:

\( f\)es continuo,
\( f\)es decreciente, y
\( f(n)=a_n\)para todos los enteros\( n≥N.\)

Entonces

\[\sum_{n=1}^∞a_n \nonumber \]

\[∫^∞_Nf(x)\,dx \nonumber \]

ambos convergen o ambos divergen (Figura\(\PageIndex{3}\)).

Si bien la convergencia de\(\displaystyle ∫^∞_Nf(x)\,dx\) implica convergencia de las series relacionadas\(\displaystyle \sum_{n=1}^∞a_n\), no implica que el valor de la integral y la serie sean los mismos. Pueden ser diferentes, y a menudo lo son. Por ejemplo,

\[\sum_{n=1}^∞\left(\dfrac{1}{e}\right)^n=\dfrac{1}{e}+\left(\dfrac{1}{e}\right)^2+\left(\dfrac{1}{e}\right)^3+⋯ \nonumber \]

es una serie geométrica con término inicial\( a=1/e\) y relación\( r=1/e,\) que converge a

\[\dfrac{1/e}{1−(1/e)}=\dfrac{1/e}{(e−1)/e}=\dfrac{1}{e−1}. \nonumber \]

Sin embargo, la integral relacionada\(\displaystyle ∫^∞_1(1/e)^x\,dx\) satisface

\[∫^∞_1\left(\frac{1}{e}\right)^x\,dx=∫^∞_1e^{−x}\,dx=\lim_{b→∞}∫^b_1e^{−x}\,dx=\lim_{b→∞}−e^{−x}\big|^b_1=\lim_{b→∞}[−e^{−b}+e^{−1}]=\dfrac{1}{e}. \nonumber \]

Ejemplo\( \PageIndex{2}\): Using the Integral Test

Para cada una de las siguientes series, utilice la prueba integral para determinar si la serie converge o diverge.

\(\displaystyle \sum_{n=1}^∞\frac{1}{n^3}\)
\(\displaystyle \sum^∞_{n=1}\frac{1}{\sqrt{2n−1}}\)

Solución

a. Comparar

\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^3}\)y\(\displaystyle ∫^∞_1\dfrac{1}{x^3}\,dx.\)

Tenemos

\(\displaystyle ∫^∞_1\dfrac{1}{x^3}\,dx=\lim_{b→∞}∫^b_1\dfrac{1}{x^3}\,dx=\lim_{b→∞}\left[−\dfrac{1}{2x^2}\bigg|^b_1\right]=\lim_{b→∞}\left[−\dfrac{1}{2b^2}+\dfrac{1}{2}\right]=\dfrac{1}{2}.\)

Así\(\displaystyle ∫^∞_1\frac{1}{x^3}\,dx\) converge la integral, y por lo tanto también lo hace la serie

\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^3}\).

b. Comparar

\(\displaystyle \sum_{n=1}^∞\dfrac{1}{\sqrt{2n−1}}\)y\(\displaystyle ∫^∞_1\dfrac{1}{\sqrt{2x−1}}\,dx\).

Desde

\(\displaystyle ∫^∞_1\frac{1}{\sqrt{2x−1}}\,dx=\lim_{b→∞}∫^b_1\frac{1}{\sqrt{2x−1}}\,dx=\lim_{b→∞}\sqrt{2x−1}\bigg|^b_1=\lim_{b→∞}\left[\sqrt{2b−1}−1\right]=∞,\)

la integral\(\displaystyle ∫^∞_1\frac{1}{\sqrt{2x−1}}\,dx\) diverge, y por lo tanto

\(\displaystyle \sum_{n=1}^∞\frac{1}{\sqrt{2n−1}}\)

diverge.

Ejercicio\( \PageIndex{2}\)

Utilice la prueba integral para determinar si la serie\(\displaystyle \sum^∞_{n=1}\dfrac{n}{3n^2+1}\) converge o diverge.

Pista: Comparar con la integral\(\displaystyle ∫^∞_1\dfrac{x}{3x^2+1}\,dx.\)
Contestar: La serie diverge.

La\(p\) serie

La serie armónica\(\displaystyle \sum^∞_{n=1}1/n\) y la serie\(\displaystyle \sum^∞_{n=1}1/n^2\) son ejemplos de un tipo de serie llamada serie p.

Definición:\(p\)-series

Para cualquier número real\( p\), la serie

\[\sum_{n=1}^∞\dfrac{1}{n^p} \nonumber \]

se llama una serie p.

Sabemos que la\(p\) -serie converge si\( p=2\) y diverge si\( p=1\). ¿Qué pasa con otros valores de\( p\)? En general, es difícil, si no imposible, calcular el valor exacto de la mayoría\( p\) de las series. Sin embargo, podemos utilizar las pruebas presentadas hasta ahora para probar si una\( p\) serie converge o diverge.

Si\( p<0,\) entonces\( 1/n^p→∞,\) y si\( p=0\), entonces\( 1/n^p→1.\) Por lo tanto, por la prueba de divergencia,

\[\sum_{n=1}^∞\dfrac{1}{n^p} \nonumber \]

diverge si\(p≤0\).

Si\( p>0,\) entonces\( f(x)=1/x^p\) es una función positiva, continua, decreciente. Por lo tanto, para\( p>0,\) nosotros utilizamos la prueba integral, comparando

\[\sum_{n=1}^∞\dfrac{1}{n^p} \nonumber \]y\[∫^∞_1\dfrac{1}{x^p}\,dx. \nonumber \]

Ya hemos considerado el caso cuando\( p=1.\) Aquí consideramos el caso cuando\( p>0,p≠1.\) Para este caso,

\[∫^∞_1\dfrac{1}{x^p}\,dx=\lim_{b→∞}∫^b_1\dfrac{1}{x^p}\,dx=\lim_{b→∞}\dfrac{1}{1−p}x^{1−p}∣^b_1=\lim_{b→∞}\dfrac{1}{1−p}[b^{1−p}−1]. \nonumber \]

Porque

\( b^{1−p}→0\)si\( p>1\) y\( b^{1−p}→∞\) si\( p<1,\)

concluimos que

\[∫^∞_1\dfrac{1}{x^p}\,dx=\begin{cases}\dfrac{1}{p−1}, \text{if}\;p>1\\ ∞, \text{if}\;p<1.\end{cases} \nonumber \]

Por lo tanto,\(\displaystyle \sum^∞_{n=1}1/n^p\) converge si\( p>1\) y diverge si\( 0<p<1.\)

En resumen,

\[\sum_{n=1}^∞\dfrac{1}{n^p}\quad \begin{cases}\text{converges} \text{if}\; p>1\\ \text{diverges} \text{if}\;p≤1\end{cases} \nonumber \].

Ejemplo\( \PageIndex{3}\): Testing for Convergence of p-series

Para cada una de las siguientes series, determine si converge o diverge.

\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^4}\)
\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^{2/3}}\)

Solución

Esta es una\(p\) -serie con\( p=4>1\), por lo que la serie converge.
Dado que\( p=2/3<1,\) la serie diverge.

Ejercicio\( \PageIndex{3}\)

¿La serie\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^{5/4}}\) converge o diverge?

Pista: \( p=5/4\)
Contestar: La serie converge.

Estimación del valor de una serie

Supongamos que sabemos que una serie\(\displaystyle \sum_{n=1}^∞a_n\) converge y queremos estimar la suma de esa serie. Ciertamente podemos aproximar esa suma usando cualquier suma finita\(\displaystyle \sum_{n=1}^Na_n\) donde\( N\) esté cualquier entero positivo. La pregunta que abordamos aquí es, para una serie convergente\(\displaystyle \sum^∞_{n=1}a_n\), ¿qué tan buena es la aproximación\(\displaystyle \sum^N_{n=1}a_n\)?

Más específicamente, si dejamos

\[R_N=\sum_{n=1}^∞a_n−\sum_{n=1}^Na_n \nonumber \]

ser el resto cuando la suma de una serie infinita se aproxima por la suma\(N^{\text{th}}\) parcial, ¿qué tan grande es\( R_N\)? Para algunos tipos de series, podemos utilizar las ideas de la prueba integral para estimar\( R_N\).

Nota\(\PageIndex{1}\): Remainder Estimate from the Integral Test

Supongamos que\(\displaystyle \sum^∞_{n=1}a_n\) es una serie convergente con términos positivos. Supongamos que existe una función que\( f\) satisface las siguientes tres condiciones:

\( f\)es continuo,
\( f\)es decreciente, y
\( f(n)=a_n\)para todos los enteros\( n≥1.\)

\( S_N\)Sea la suma\(N^{\text{th}}\) parcial de\(\displaystyle \sum^∞_{n=1}a_n\). Para todos los enteros positivos\( N\),

\[S_N+∫^∞_{N+1}f(x)\,dx<\sum_{n=1}^∞a_n<S_N+∫^∞_Nf(x)\,dx. \nonumber \]

Es decir, el resto\(\displaystyle R_N=\sum^∞_{n=1}a_n−S_N=\sum^∞_{n=N+1}a_n\) satisface la siguiente estimación:

\[∫^∞_{N+1}f(x)\,dx<R_N<∫^∞_Nf(x)\,dx. \nonumber \]

Esto se conoce como la estimación del resto.

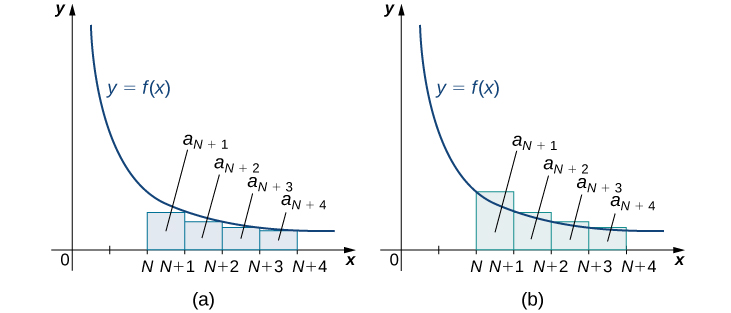
Ilustramos Nota\(\PageIndex{1}\) en Figura\(\PageIndex{4}\). En particular, al representar el resto\( R_N=a_{N+1}+a_{N+2}+a_{N+3}+⋯\) como la suma de áreas de rectángulos, vemos que el área de esos rectángulos está delimitada arriba por\(\displaystyle ∫^∞_Nf(x)\,dx\) y delimitada abajo por\(\displaystyle ∫^∞_{N+1}f(x)\,dx.\) En otras palabras,

\[R_N=a_{N+1}+a_{N+2}+a_{N+3}+⋯>∫^∞_{N+1}f(x)\,dx \nonumber \]

\[R_N=a_{N+1}+a_{N+2}+a_{N+3}+⋯<∫^∞_Nf(x)\,dx. \nonumber \]

Concluimos que

\[∫^∞_{N+1}f(x)\,dx<R_N<∫^∞_Nf(x)\,dx. \nonumber \]

Desde

\[\sum_{n=1}^∞a_n=S_N+R_N, \nonumber \]

donde\( S_N\) esta la suma\(N^{\text{th}}\) parcial, concluimos que

\[S_N+∫^∞_{N+1}f(x)\,dx<\sum_{n=1}^∞a_n<S_N+∫^∞_Nf(x)\,dx. \nonumber \]

Esto muestra dos gráficas lado a lado de la misma función decreciente cóncava hacia arriba y = f (x) que se aproxima al eje x en el cuadrante 1. Los rectángulos se dibujan con una base de 1 sobre los intervalos N a N + 4. Las alturas de los rectángulos en la primera gráfica están determinadas por el valor de la función en los extremos derechos de las bases, y las de la segunda gráfica están determinadas por el valor en los extremos izquierdos de las bases. Las áreas de los rectángulos están marcadas: a_ (N + 1), a_ (N + 2), a través de a_ (N + 4). — Figura\(\PageIndex{4}\): Dada una función continua, positiva, decreciente\( f\) y una secuencia de términos positivos\( a_n\) tal que\( a_n=f(n)\) para todos los enteros positivos\( n\), (a) las áreas\(\displaystyle a_{N+1}+a_{N+2}+a_{N+3}+⋯<∫^∞_Nf(x)\,dx\)*, o (b) las áreas\(\displaystyle a_{N+1}+a_{N+2}+a_{N+3}+⋯>∫^∞_{N+1}f(x)\,dx\). Por lo tanto, la integral es una sobreestimación o una subestimación del error.*

Ejemplo\( \PageIndex{4}\): Estimating the Value of a Series

Considera la serie\(\displaystyle \sum^∞_{n=1}\frac{1}{n^3}\).

Calcular\(\displaystyle S_{10}=\sum^{10}_{n=1}\frac{1}{n^3}\) y estimar el error.
Determinar el menor valor de lo\( N\) necesario tal que\( S_N\) estimará\(\displaystyle \sum^∞_{n=1}\frac{1}{n^3}\) a dentro\( 0.001\).

Solución

a. Utilizando una utilidad de cálculo, tenemos

\[ S_{10}=1+\dfrac{1}{2^3}+\dfrac{1}{3^3}+\dfrac{1}{4^3}+⋯+\dfrac{1}{10^3}≈1.19753. \nonumber \]

Por la estimación del resto, sabemos

\[ R_N<∫^∞_N\dfrac{1}{x^3}\,dx. \nonumber \]

Tenemos

\[ ∫^∞_{10}\dfrac{1}{x^3}\,dx=\lim_{b→∞}∫^b_{10}\dfrac{1}{x^3}\,dx=\lim_{b→∞}\left[−\dfrac{1}{2x^2}\right]^b_N=\lim_{b→∞}\left[−\dfrac{1}{2b^2}+\dfrac{1}{2N^2}\right]=\dfrac{1}{2N^2}. \nonumber \]

Por lo tanto, el error es\( R_{10}<1/2(10)^2=0.005.\)

b. encontrar\( N\) tal que\( R_N<0.001\). En la parte a. lo demostramos\( R_N<1/2N^2\). Por lo tanto, el resto\( R_N<0.001\) siempre y cuando\( 1/2N^2<0.001\). Es decir, necesitamos\( 2N^2>1000\). Resolviendo esta desigualdad para\( N\), vemos que necesitamos\( N>22.36\). Para asegurar que el resto esté dentro de la cantidad deseada, necesitamos redondear hasta el entero más cercano. Por lo tanto, el valor mínimo necesario es\( N=23\).

Ejercicio\( \PageIndex{4}\)

Para\(\displaystyle \sum^∞_{n=1}\frac{1}{n^4}\), calcular\( S_5\) y estimar el error\( R_5\).

Pista: Usar la estimación del resto\(\displaystyle R_N<∫^∞_N\frac{1}{x^4}\,dx.\)
Contestar: \( S_5≈1.09035, R_5<0.00267\)

Conceptos clave

Si\(\displaystyle \lim_{n→∞}a_n≠0,\) entonces la serie\(\displaystyle \sum^∞_{n=1}a_n\) diverge.
Si\(\displaystyle \lim_{n→∞}a_n=0,\) la serie\(\displaystyle \sum^∞_{n=1}a_n\) puede converger o divergir.
Si\(\displaystyle \sum^∞_{n=1}a_n\) es una serie con términos positivos\( a_n\) y\( f\) es una función continua, decreciente tal que\( f(n)=a_n\) para todos los enteros positivos\( n\), entonces

\[\sum_{n=1}^∞a_n \nonumber \]y\[∫^∞_1f(x)\,dx \nonumber \]

ambos convergen o ambos divergen. Además, si\(\displaystyle \sum^∞_{n=1}a_n\) converge, entonces la aproximación de la suma\(N^{\text{th}}\) parcial\( S_N\) es precisa hasta un error\( R_N\) donde\(\displaystyle ∫^∞_{N+1}f(x)\,dx<R_N<∫^∞_Nf(x)\,dx\).

La\(p\) serie\(\displaystyle \sum_{n=1}^∞\frac{1}{n^p}\) -converge si\( p>1\) y diverge si\( p≤1.\)

Ecuaciones Clave

Prueba de divergencia

Si\( a_n↛0\) como\(\displaystyle n→∞,\sum_{n=1}^∞a_n\) diverge.

serie p

\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^p}\quad \begin{cases}\text{converges}, \text{if}\;p>1\\\text{diverges}, \text{if}\; p≤1\end{cases}\)

Estimación del resto de la prueba integral

\(\displaystyle ∫^∞_{N+1}f(x)\,dx<R_N<∫^∞_Nf(x)\,dx\)

Glosario

prueba de divergencia: si\(\displaystyle \lim_{n→∞}a_n≠0,\) entonces la serie\(\displaystyle \sum^∞_{n=1}a_n\) diverge

prueba integral

para una serie\(\displaystyle \sum^∞_{n=1}a_n\) con términos positivos\( a_n\), si existe una función continua, decreciente\( f\) tal que\( f(n)=a_n\) para todos los enteros positivos\( n\), entonces

\[\sum_{n=1}^∞a_n \nonumber \]y\[∫^∞_1f(x)\,dx \nonumber \]

ambos convergen o ambos divergen

serie p: una serie de la forma\(\displaystyle \sum^∞_{n=1}1/n^p\)

estimación del resto

para una serie\(\displaystyle \sum^∞_{n=}1a_n\) con términos positivos\( a_n\) y una función continua decreciente\( f\) tal que\( f(n)=a_n\) para todos los enteros positivos\( n\), el resto\(\displaystyle R_N=\sum^∞_{n=1}a_n−\sum^N_{n=1}a_n\) satisfaga la siguiente estimación:

\[∫^∞_{N+1}f(x)\,dx<R_N<∫^∞_Nf(x)\,dx \nonumber \]