13.6: Volumen entre Superficies y Triple Integración
- Page ID
- 111821
Aprendimos en la Sección 13.2 cómo calcular el volumen firmado\(V\) bajo una superficie\(z=f(x,y)\) sobre una región\(R\):\(V = \iint_R f(x,y) dA\). De ello se deduce naturalmente que si está\(f(x,y)\geq g(x,y)\) encendido\(R\), entonces el volumen entre\(f(x,y)\) y\(g(x,y)\) on\(R\) es
\[ \begin{align} V &= \iint_R f(x,y) dA - \iint_R g(x,y) dA \\[4pt] &= \iint_R \big(f(x,y)-g(x,y)\big) dA. \end{align} \]
teorema 124: Volumen entre Superficies
Dejar\(f\) y\(g\) ser funciones continuas en una región cerrada y delimitada\(R\), donde\(f(x,y)\geq g(x,y)\) para todos\((x,y)\) adentro\(R\). El volumen\(V\) entre\(f\) y\(g\) más\(R\) es
\[V =\iint_R \big(f(x,y)-g(x,y)\big) dA.\]
Ejemplo\(\PageIndex{1}\): Finding volume between surfaces
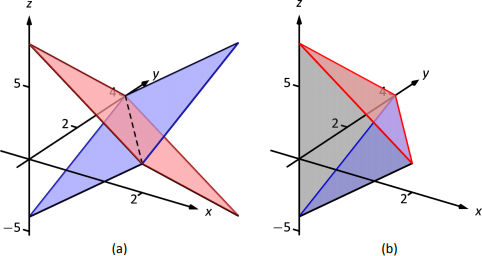
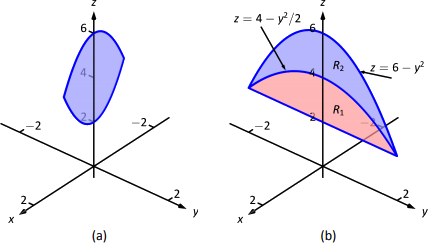
Encuentra el volumen de la región espacial delimitada por los planos\(z=3x+y-4\) y\(z=8-3x-2y\) en el\(1^\text{st}\) octante. En la Figura 13.36 (a) se dibujan los planos; en (b), solo se da la región definida.
Solución
Tenemos que determinar la región\(R\) sobre la que nos integraremos. Para ello, necesitamos determinar dónde se cruzan los planos. Tienen\(z\) valores comunes cuando\(3x+y-4=8-3x-2y\). Aplicando un poco de álgebra, tenemos:
\ [\ comenzar {alinear*}
3x+y-4 &= 8-3x-2y\\
6x+3y &=12\\
2x+y &=4
\ final {alinear*}\]
Los planos se cruzan a lo largo de la línea\(2x+y=4\). Por lo tanto la región\(R\) está delimitada por\(x=0\)\(y=0\),, y\(y=4-2x\); podemos convertir estos límites en límites de integración de\(0\leq x\leq 2\),\(0\leq y\leq 4-2x\). Por lo tanto
\ [\ begin {align*}
V &=\ iInt_r\ grande (8-3x-2y- (3x+y-4)\ grande) dA\\
&=\ int_0^2\ int_0^ {4-2x}\ grande (12-6x-3y\ grande) dy\, dx\
&= 16\ texto {u} ^3.
\ end {alinear*}\]
El volumen entre las superficies es de unidades\(16\) cúbicas.
En el ejemplo anterior, encontramos el volumen evaluando la integral\[ \int_0^2\int_0^{4-2x} \big(8-3x-2y-(3x+y-4)\big) dy \, dx.\] Note como podemos reescribir el integrando como integral, tanto como lo hicimos en la Sección 13.1:
\[8-3x-2y-(3x+y-4) = \int_{3x+y-4}^{8-3x-2y} dz.\]
Así podemos reescribir la doble integral que encuentra volumen como
\[\int_0^2\int_0^{4-2x} \big(8-3x-2y-(3x+y-4)\big) dy \, dx = \int_0^2\int_0^{4-2x}\left(\int_{3x+y-4}^{8-3x-2y} dz\right) dy \, dx.\]
Esto ya no parece una “doble integral”, sino más bien una “triple integral”. Así como nuestra primera introducción a las dobles integrales fue en el contexto de encontrar el área de una región plana, nuestra introducción en triples integrales será en el contexto de encontrar el volumen de una región espacial.
Para encontrar formalmente el volumen de una región cerrada y delimitada\(D\) en el espacio, como la que se muestra en la Figura 13.37 (a), se inicia con una aproximación. Romper\(D\) en sólidos\(n\) rectangulares; los sólidos cerca del límite de\(D\) posiblemente no incluyan porciones de\(D\) y/o incluyan espacio adicional. En la Figura 13.37 (b), ampliamos una porción del límite de\(D\) para mostrar un sólido rectangular que no contiene espacio\(D\); ya que esta es una aproximación del volumen, esto es aceptable y este error se reducirá a medida que encojamos el tamaño de nuestros sólidos.
El volumen\(\Delta V_i\) del\(i^\text{th}\) sólido\(D_i\) es\(\Delta V_i = \Delta x_i\Delta y_i\Delta z_i\), donde\(\Delta x_i\),\(\Delta y_i\) y\(\Delta z_i\) dar las dimensiones del sólido rectangular en las\(z\) direcciones\(x\),\(y\) y, respectivamente. Al resumir los volúmenes de todos los\(n\) sólidos, obtenemos una aproximación del volumen\(V\) de\(D\):
$$V\ approx\ suma_ {i=1} ^n\ Delta V_i =\ suma_ {i=1} ^n\ Delta x_i\ Delta y_i\ Delta z_i.\]
Let\(||\Delta D||\) representar la longitud de la diagonal más larga de sólidos rectangulares en la subdivisión de\(D\). Como\(||\Delta D||\to 0\), el volumen de cada sólido va a 0, al igual que cada uno de\(\Delta x_i\),\(\Delta y_i\) y\(\Delta z_i\), para todos\(i\). Nuestra experiencia en cálculo nos dice que tomar un límite como\(||\Delta D||\to 0\) convierte nuestra aproximación de\(V\) en un cálculo exacto de\(V\). Antes de exponer este resultado en un teorema, utilizamos una definición para definir algunos términos.
Definición 106: Integrales triples, integración iterada (Parte I)
Dejar\(D\) ser una región cerrada y delimitada en el espacio. Dejar\(a\) y\(b\) ser números reales, dejar\(g_1(x)\) y\(g_2(x)\) ser funciones continuas de\(x\), y dejar\(f_1(x,y)\) y\(f_2(x,y)\) ser funciones continuas de\(x\) y\(y\).
- El volumen\(V\) de\(D\) se denota por una triple integral, $$V =\ IIint_D dV. $$
- La integral iterada\( \int_a^b\int_{g_1(x)}^{g_2(x)}\int_{f_1(x,y)}^{f_2(x,y)} dz \, dy \, dx\) se evalúa como
$$\ int_a^b\ int_ {g_1 (x)} ^ {g_2 (x)}\ int_ {f_1 (x, y)} ^ {f_2 (x, y)} dz\, dy\, dx=\ int_a^b\ int_ {g_1 (x)} ^ {g_2 (x)}\ left (\ int_ {f_1 (x, y)} ^ {f_2 (x, y)} dz\ derecha) dy\, dx. $$
Evaluar la integral iterada anterior es triple integración.
Nuestra comprensión informal de la notación\(\iiint_D dV\) es “resumir muchos pequeños volúmenes”\(D\), análoga a nuestra comprensión de\(\iint_R dA\) y\(\iint_R\ dm\).
Ahora exponemos el teorema mayor de esta sección.
teorema 125 Triple Integración (Parte I)
Dejar\(D\) ser una región cerrada, delimitada en el espacio y dejar\(\Delta D\) ser cualquier subdivisión de\(D\) en sólidos\(n\) rectangulares, donde la\(i^\text{th}\) subregión\(D_i\) tiene dimensiones\(\Delta x_i\times\Delta y_i\times\Delta z_i\) y volumen\(\Delta V_i\).
- El volumen\(V\) de\(D\) es
$$V =\ IIint_D dV =\ lim_ {||\ Delta D||\ to0}\ suma_ {i=1} ^n\ Delta V_i =\ lim_ {||\ Delta D||\ to0}\ suma_ {i=1} ^n\ Delta x_i\ Delta y_i\ Delta z_i.$$ - Si\(D\) se define como la región delimitada por los planos\(x=a\) y\(x=b\), los cilindros\(y=g_(x)\) y\(y=g_2(x)\), y las superficies\(z=f_1(x,y)\) y\(z=f_2(x,y)\), donde\(a<b\),\(g_1(x)\leq g_2(x)\) y\(f_1(x,y)\leq f_2(x,y)\) en\(D\), entonces
$$\ IIint_D dV =\ int_a^b\ int_ {g_1 (x)} ^ {g_2 (x) )}\ int_ {f_1 (x, y)} ^ {f_2 (x, y)} dz\, dy\, dx. $$ - \(V\)se puede determinar mediante la integración iterada con otros órdenes de integración (hay 6 en total), siempre y cuando\(D\) se defina por la región encerrada por un par de planos, un par de cilindros y un par de superficies.
Se evaluó el área de una región plana\(R\) mediante integración iterada, donde los límites fueron “de curva a curva, luego de punto a punto”. El teorema 125 nos permite encontrar el volumen de una región espacial con una integral iterada con límites “de superficie a superficie, luego de curva a curva, luego de punto a punto”. En la integral iterada
\[\int_a^b\int_{g_1(x)}^{g_2(x)}\int_{f_1(x,y)}^{f_2(x,y)} dz \, dy \, dx,\]
los límites\(a\leq x\leq b\) y\(g_1(x)\leq y\leq g_2(x)\) definir una región\(R\) en el\(x\) -\(y\) plano sobre el cual\(D\) existe la región en el espacio. Sin embargo, estos límites también están definiendo superficies en el espacio;\(x=a\) es un plano y\(y=g_1(x)\) es un cilindro. La combinación de estas 6 superficies encierran, y definen,\(D\).
Los ejemplos nos ayudarán a entender la triple integración, incluida la integración con varios órdenes de integración.
Ejemplo\(\PageIndex{2}\): Finding the volume of a space region with triple integration
Encontrar el volumen de la región espacial en el\(1^{\,st}\) octante delimitado por el plano\(z=2-y/3-2x/3\), mostrado en la Figura 13.38 (a), utilizando el orden de integración\(dz \, dy \, dx\). Configura las triples integrales que dan el volumen en los otros 5 órdenes de integración.
Solución
Comenzando por el orden de integración\(dz \, dy \, dx\), primero tenemos que encontrar límites en\(z\). La región\(D\) está delimitada abajo por el plano\(z=0\) (porque estamos restringidos al primer octante) y arriba por\(z=2-y/3-2x/3\);\(0\leq z\leq 2-y/3-2x/3\).
Para encontrar los límites en\(y\) y\(x\), “colapsamos” la región en el\(y\) plano\(x\) -, dando el triángulo que se muestra en la Figura 13.38 (b). (Conocemos la ecuación de la línea\(y=6-2x\) de dos maneras. Primero, fijando\(z=0\), tenemos\(0 = 2-y/3-2x/3 \Rightarrow y=6-2x\). En segundo lugar, sabemos que esta va a ser una línea recta entre los puntos\((3,0)\) y\((0,6)\) en el\(y\) plano\(x\) -.)
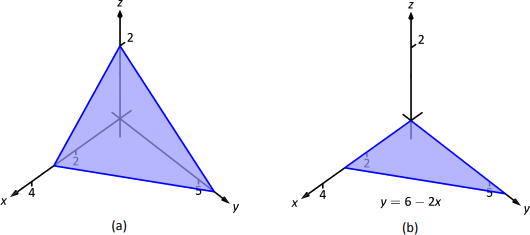
Definimos esa región\(R\), en el orden de integración de\(dy \, dx\), con límites\(0\leq y\leq 6-2x\) y\(0\leq x\leq 3\). Así el volumen\(V\) de la región\(D\) es:
\ [\ begin {align*}
V &=\ IIint_d dV\\
&=\ int_0^3\ int_0^ {6-2x}\ int_0^ {2-\ frac 13y-\ frac 23x} dz dy dz\\
&=\ int_0^3\ int_0^ {6-2x}\ izquierda (\ int_0^ {2-\ frac 13y-\ frac 23x} dz\ derecha) dy dz\\
&=\ int_0^3\ int_0^ {6-2x} z\ Big|_0^ {2-\ frac 13y-\ frac 23x} dy dz\\
&=\ int_0^3\ int_0^ {6-2x}\ izquierda (2-\ frac 13y-\ frac 23x\ derecha) dy dz. \ end {align*}\]
A partir de este paso, estamos evaluando una doble integral como se hizo muchas veces antes. Nos saltamos estos pasos y damos el volumen final,
\[= 6\text{u}^3. \]
El orden\(dz \, dx \, dy\):
Ahora considere el volumen usando el orden de integración\(dz \, dx \, dy\). Los límites en\(z\) son los mismos que antes,\(0\leq z\leq 2-y/3-2x/3\). Al colapsar la región espacial en el\(y\) plano\(x\) - como se muestra en la Figura 13.38 (b), ahora describimos este triángulo con el orden de integración\(dx dy\). Esto da límites\(0\leq x\leq 3-y/2\) y\(0\leq y\leq 6\). Así el volumen viene dado por la triple integral
\[V = \int_0^6\int_0^{3-\frac12y}\int_0^{2-\frac13y-\frac23x} dz \, dx \, dy.\]
El orden\(dx \, dy \, dz\):
Siguiendo nuestra estrategia de\(\ldots\) “superficie a superficie”, necesitamos determinar las\(x\) superficies que unen nuestra región espacial. Para ello, acércate a la región “desde atrás”, en la dirección de aumentar\(x\). La primera superficie que golpeamos al entrar en la región es el\(z\) plano\(y\) -, definido por\(x=0\). Nosotros salimos de la región en el avión\(z=2-y/3-2x/3\); resolviendo para\(x\), tenemos\(x= 3-y/2-3z/2\). Así los límites en\(x\) son:\(0\leq x\leq 3-y/2-3z/2\).
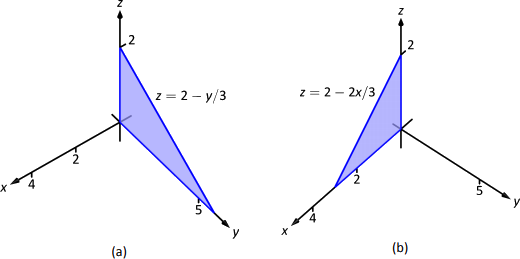
Ahora colapsar la región espacial en el\(z\) plano\(y\) -, como se muestra en la Figura 13.39 (a). (Nuevamente, encontramos la ecuación de la línea\(z=2-y/3\) estableciendo\(x=0\) en la ecuación\(x=3-y/2-3z/2\).) Tenemos que encontrar límites en esta región con el orden\(dy dz\). Las curvas que\(y\) enlazan son\(y=0\) y\(y=6-3z\); los puntos que\(z\) enlazan son 0 y 2. Así, el volumen de entrega integral triple es:
\ [\ begin {array} {cc}
\ begin {array} {c}
0\ leq x\ leq 3-y/2-3z/2\\
0\ leq y\ leq 6-3z\\
0\ leq z\ leq 2
\ end {array}
&
\ Rightarrow\ quad\ int_0^2\ int_0^ {6-3z}\ int_0^ {3-y/2-3z z/2} dx\, dy\, dz.
\ end {array}
\]
El orden\(dx \, dz \, dy\):
Los\(x\) límites son los mismos que el orden anterior. Consideramos ahora el triángulo en la Figura 13.39 (a) y lo describimos con el orden\(dz dy\):\(0\leq z\leq 2-y/3\) y\(0\leq y\leq 6\). Así el volumen viene dado por:
$$\ begin {array} {cc}
\ begin {array} {c}
0\ leq x\ leq 3-y/2-3z/2\\
0\ leq z\ leq 2-y/3\\
0\ leq y\ leq 6
\ end {array}
&
\ Rightarrow\ quad\ int_0^6\ int_0^ {2-y/3}\ int_0^ ^ {3-y/2-3z/2} dx\, dz\, dy.
\ end {array}
\]
El orden\(dy dz dx\):
Ahora necesitamos determinar las\(y\) superficies que determinan nuestra región. Acercándonos a la región espacial desde “atrás” y moviéndonos en la dirección de aumentar\(y\), primero ingresamos a la región en\(y=0\), y salimos a lo largo del avión\(z= 2-y/3-2x/3\). Resolviendo para\(y\), este plano tiene ecuación\(y = 6-2x-3z\). Así\(y\) tiene límites\(0\leq y\leq 6-2x-3z\).
Ahora colapsar la región sobre el\(z\) plano\(x\) -, como se muestra en la Figura 13.39 (b). Las curvas que delimitan este triángulo son\(z=0\) y\(z=2-2x/3\);\(x\) está delimitada por los puntos\(x=0\) a\(x=3\). Así el triple integral dando volumen es:
$$\ begin {array} {cc}
\ begin {array} {c}
0\ leq y\ leq 6-2x-3z\\
0\ leq z\ leq 2-2x/3\
0\ leq x\ leq 3
\ end {array}
&
\ Rightarrow\ quad\ int_0^3\ int_ 0^ {2-2x/3}\ int_0^ {6-2x-3z} dy dz dx.
\ end {array}
\]
El orden\(dy \, dx \, dz\):
Los\(y\) límites son los mismos que en el orden anterior. Ahora determinamos los límites del triángulo en la Figura 13.39 (b) usando el orden\(dy \, dx \, dz\). \(x\)está delimitado por\(x=0\) y\(x=3-3z/2\);\(z\) está delimitado entre\(z=0\) y\(z=2\). Esto lleva a la triple integral:
\ [\ begin {array} {cc}
\ begin {array} {c}
0\ leq y\ leq 6-2x-3z\\
0\ leq x\ leq 3-3z/2\\
0\ leq z\ leq 2
\ end {array}
&
\ Rightarrow\ quad\ int_0^2\ int_0^ {3-3z/2}\ int_0^ {6-2x-3z} dy\, dx\, dz.
\ end {array}
\]
Este problema fue largo, pero ojalá útil, demostrando cómo determinar límites con cada orden de integración para describir la región\(D\). En la práctica, solo necesitamos 1, pero poder hacerlas todas nos da flexibilidad para elegir el orden que más nos convenga.
En el ejemplo anterior, colapsamos la superficie en los\(z\) planos\(x\)\(x\) -\(y\)\(z\),\(y\) - y - a medida que determinamos los límites de integración “curva a curva, punto a punto”. Como la superficie era una porción triangular de un plano, este colapso, o proyección, era simple: la proyección de una línea recta en el espacio sobre un plano de coordenadas es una línea.
El siguiente ejemplo nos muestra cómo hacer esto cuando se trata de superficies y curvas más complicadas.
Ejemplo\(\PageIndex{3}\): Finding the projection of a curve in space onto the coordinate planes
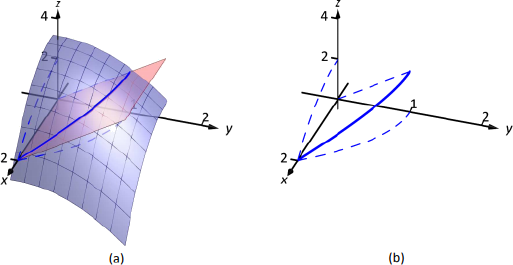
Considere las superficies\(z=3-x^2-y^2\) y\(z=2y\), como se muestra en la Figura 13.40 (a). Se muestra la curva de su intersección, junto con la proyección de esta curva hacia los planos de coordenadas, que se muestra discontinua. Encuentra las ecuaciones de las proyecciones en los planos de coordenadas.
Solución
Las dos superficies son\(z=3-x^2-y^2\) y\(z=2y\). Para encontrar dónde se cruzan, es natural establecerlos iguales entre sí:\(3-x^2-y^2=2y\). Esta es una función implícita de\(x\) y\(y\) que da todos los puntos\((x,y)\) en el\(y\) plano\(x\) - donde los\(z\) valores de las dos superficies son iguales.
Podemos reescribir esta función implícita completando el cuadrado:
$$3-x^2-y^2=2y\ quad\ Rightarrow\ quad y^2+2y+x^2=3\ quad\ Rightarrow\ quad (y+1) ^2+x^2=4. $$
Así, en el\(y\) plano\(x\) - la proyección de la intersección es un círculo con radio 2, centrado en\((0,-1)\).
Para proyectar sobre el\(z\) plano\(x\) -, hacemos un procedimiento similar: encontrar los\(z\) valores\(x\) y donde los\(y\) valores en la superficie son los mismos. Comenzamos resolviendo la ecuación de cada superficie para\(y\). En este caso particular, funciona bien para resolver realmente\(y^2\):
\(z=3-x^2-y^2 \quad \Rightarrow \quad y^2=3-x^2-z\)
\(z=2y \quad \Rightarrow \quad y^2=z^2/4\).
Así tenemos (después de completar nuevamente el cuadrado):
$$3-x^2-z = z^2/4\ quad\ Rightarrow\ quad\ frac {(z+2) ^2} {16} +\ frac {x^2} 4=1, $$
y elipse centrada\((0,-2)\) en el\(z\) plano\(x\) - con un eje mayor de longitud 8 y un eje menor de longitud 4.
Finalmente, para proyectar la curva de intersección en el\(z\) plano\(y\) -, resolvemos la ecuación para\(x\). Dado que\(z=2y\) es un cilindro que carece de la variable\(x\), se convierte en nuestra ecuación de la proyección en el\(z\) plano\(y\) -.
Las tres proyecciones se muestran en la Figura 13.40 (b).
Ejemplo\(\PageIndex{4}\): Finding the volume of a space region with triple integration
Configurar las integrales triples que encuentran el volumen de la región espacial\(D\) delimitada por las superficies\(x^2+y^2=1\),\(z=0\) y\(z=-y\), como se muestra en la Figura 13.41 (a), con los órdenes de integración\(dz \, dy \, dx\),\(dy \, dx \, dz\) y\(dx \, dz \, dy\).
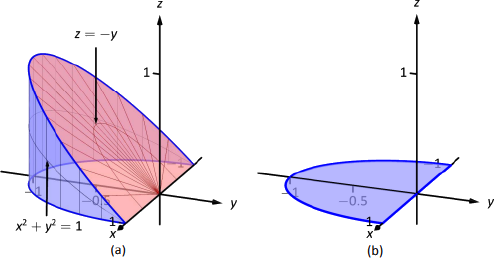
Solución
El orden\(dz \, dy \, dx\):
La región\(D\) está delimitada por debajo por el plano\(z=0\) y arriba por el plano\(z=-y\). El cilindro\(x^2+y^2=1\) no ofrece ningún límite en la\(z\) dirección, ya que esa superficie es paralela al\(z\) eje. Por lo tanto\(0\leq z\leq -y\).
Al colapsar la región en el\(y\) plano\(x\) -, obtenemos parte del círculo con ecuación\(x^2+y^2=1\) como se muestra en la Figura 13.41 (b). En función de\(x\), este semicírculo tiene ecuación\(y=-\sqrt{1-x^2}\). Así\(y\) queda delimitado abajo por\(-\sqrt{1-x^2}\) y arriba por\(y=0\):\(-\sqrt{1-x^2}\leq y\leq 0\). Los\(x\) límites del semicírculo son\(-1\leq x\leq 1\). En conjunto, los límites de integración y triple integral son los siguientes:
\ [\ begin {array} {cc}
\ begin {array} {c}
0\ leq z\ leq -y\
-\ sqrt {1-x^2}\ leq y\ leq 0\\
-1\ leq x\ leq 1
\ end {array}
&
\ Rightarrow\ quad\ int_ {-1} ^1\ int_ {-\ sqrt {1-x^2} ^ {0}\ int_0^ {-y} dz\, dy\, dx.
\ end {array}
\]
Evaluamos esta triple integral:
\ [\ begin {alinear*}
\ int_ {-1} ^1\ int_ {-\ sqrt {1-x^2}} ^ {0}\ int_0^ {-y} dz\, dy\, dx &=\ int_ {-1} ^1\ int_ {-\ sqrt {1-x^2}} ^ {0}\ big (-y\ big dy\, dx\\
&=\ int_ {-1} ^1\ grande (-\ frac12y^2\ grande)\ Big|_ {-\ sqrt {1-x^2}} ^ {0} dx\\
&=\ int_ {-1} ^1\ frac12\ grande (1-x^2\ grande) dx\\
&=\ izquierda. \ izquierda (\ frac12\ izquierda (x-\ frac13x^3\ derecha)\ derecha)\ derecha|_ {-1} ^1\\
&=\ frac23\ texto {unidades} ^3.
\ end {alinear*}\]
Con el pedido\(dy \, dx \, dz\):
La región está delimitada “por debajo” en la\(y\) dirección -por la superficie\(x^2+y^2=1 \Rightarrow y=-\sqrt{1-x^2}\) y “arriba” por la superficie\(y=-z\). Así son\(y\) los límites\(-\sqrt{1-x^2}\leq y\leq -z\).
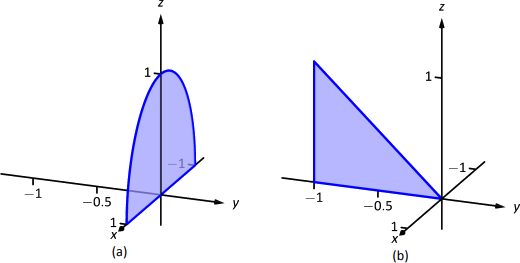
Al colapsar la región sobre el\(z\) plano\(x\) - se obtiene la región que se muestra en la Figura 13.42 (a); este semicírculo tiene ecuación\(x^2+z^2=1\). (Encontramos esta curva resolviendo cada superficie para\(y^2\), luego establecerlas iguales entre sí. Tenemos\(y^2=1-x^2\) y\(y=-z\Rightarrow y^2=z^2\). Así\(x^2+z^2=1\).) Está delimitado abajo por\(x=-\sqrt{1-z^2}\) y arriba por\(x=\sqrt{1-z^2}\), donde\(z\) está delimitado por\(0\leq z\leq 1\). Todos juntos, tenemos:
\ [\ begin {array} {cc}
\ begin {array} {c}
-\ sqrt {1-x^2}\ leq y\ leq -z\
-\ sqrt {1-z^2}\ leq x\ leq\ leq\ sqrt {1-z^2}\\
0\ leq z\ leq 1
\ end {array}
&
\ Rightarrow\ quad\ int_ {0} ^1\ int_ {-\ sqrt {1-z^2}} ^ {\ sqrt {1-z^2}}\ int_ {-\ sqrt {1-x^2}} ^ {-z} dy\, dx\, dz.
\ end {array}
\]
Con el pedido\(dx \, dz \, dy\):
\(D\)está delimitado por debajo por la superficie\(x=-\sqrt{1-y^2}\) y arriba por\(\sqrt{1-y^2}\). Luego colapsamos la región en el\(z\) plano\(y\) - y obtenemos el triángulo que se muestra en la Figura 13.42} (b). (La hipotenusa es la línea\(z=-y\), igual que el plano). Por lo tanto,\(z\) está delimitado por\(0\leq z\leq -y\) y\(y\) está delimitado por\(-1\leq y\leq 0\). Esto da:
\ [\ begin {array} {cc}
\ begin {array} {c}
-\ sqrt {1-y^2}\ leq x\ leq\ leq\ sqrt {1-y^2}\\
0\ leq z\ leq -y\\
-1\ leq y\ leq 0
\ end {array}
&
\ Rightarrow\ quad\ int_ {-1} ^0\ int_ {0} {-y}\ int_ {-\ sqrt {1-y^2}} ^ {\ sqrt {1-y^2}} dx\ , dz\, dy.
\ end {array}
\]
El siguiente teorema afirma dos cosas que deberían tener “sentido común” para nosotros. Primero, usar la triple integral para encontrar el volumen de una región siempre\(D\) debe devolver un número positivo; estamos calculando el volumen aquí, no el volumen firmado. En segundo lugar, para calcular el volumen de una región “complicada”, podríamos dividirla en subregiones y computar los volúmenes de cada subregión por separado, sumarlos posteriormente para encontrar el volumen total.
TEORMA 126: Propiedades de las Integrales Triples
Dejar\(D\) ser una región cerrada, delimitada en el espacio, y dejar\(D_1\) y\(D_2\) ser regiones no superpuestas de tal manera que\(D=D_1\bigcup D_2\).
- \( \iiint_D dV \geq 0\)
- \( \iiint_D dV = \iiint_{D_1} dV + \iiint_{D_2} dV.\)
Usamos esta última propiedad en el siguiente ejemplo.
Ejemplo\(\PageIndex{5}\): Finding the volume of a space region with triple integration
Encuentre el volumen de la región espacial\(D\) delimitada por los planos de coordenadas,\(z=1-x/2\) y\(z=1-y/4\), como se muestra en la Figura 13.43 (a). Configura las triples integrales que encuentran el volumen de\(D\) en los 6 órdenes de integración.
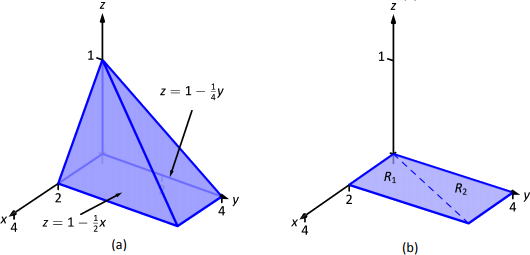
Solución
Siguiendo los límites, determinando la estrategia de “superficie a superficie, curva a curva y punto a punto”, podemos ver que los órdenes de integración más difíciles son los dos en los que integramos con respecto a la\(z\) primera, porque hay dos superficies “superiores” que atado\(D\) en la\(z\) dirección -. Entonces empezamos por señalar que tenemos
\[0\leq z\leq 1-\frac12x \quad\text{and}\quad 0\leq z\leq 1-\frac14y.\]
Ahora colapsamos la región\(D\) sobre el\(y\) eje\(x\) -, como se muestra en la Figura 13.43 (b). El límite de\(D\), la línea de\((0,0,1)\) a\((2,4,0)\), se muestra en la parte (b) de la figura como una línea discontinua; tiene ecuación\(y=2x\). (Podemos reconocer esto de dos maneras: una, al colapsar la línea de\((0,0,1)\) a\((2,4,0)\) sobre el\(y\) plano\(x\) -, simplemente ignoramos los\(z\) -valores, es decir, la línea ahora va de\((0,0)\) a\((2,4)\). En segundo lugar, las dos superficies se encuentran donde\(z=1-x/2\) es igual a\(z=1-y/4\): por lo tanto\(1-x/2=1-y/4 \Rightarrow y=2x.\))
Utilizamos la segunda propiedad del Teorema 126 para afirmar que
\[\iiint_D dV = \iiint_{D_1} dV + \iiint_{D_2} dV,\]
donde\(D_1\) y\(D_2\) son las regiones espaciales por encima de las regiones del plano\(R_1\) y\(R_2\), respectivamente. Así podemos decir
\[\iiint_D dV = \iint_{R_1}\left(\int_0^{1-x/2} dz\right)dA + \iint_{R_2}\left(\int_0^{1-y/4} dz\right)dA.\]
Todo lo que queda es determinar los límites de\(R_1\) y\(R_2\), dependiendo de si nos estamos integrando con el orden\(dx dy\) o\(dy \, dx\). Damos aquí las integrales finales, dejando que el lector confirme estos resultados.
\(dz \, dy \, dx\):
$$\ begin {array} {ccccc}
&\ begin {array} {c}
0\ leq z\ leq 1-x/2\\
0\ leq y\ leq 2x\\
0\ leq x\ leq 2
\ end {array}
&
\ begin {array} {c}
0\ leq z\ leq 1-y/4\\
2x\ leq y\ leq 4\\
0\ leq x\ leq 2
\ end {array}\\\
\ IIint_d dV &=&\ int_0^2\ int_0^ {2x}\ int_0^ {1-x/2} dz\, dy\, dx &+&\ int_0^2\ int_ {2x} ^4\ int_0^ {1-int_0^ {y/4} dz\, dy\, dx
\ end {array}
\]
\(dz \, dx \, dy\):
$$\ begin {array} {ccccc}
&\ begin {array} {c}
0\ leq z\ leq 1-x/2\\
y/2\ leq x\ leq 2\\
0\ leq y\ leq 4
\ end {array}
&
\ begin {array} {c}
0\ leq z\ leq 1-y/4\\
0\ leq x\ leq y/2\\
0\ leq y\ leq 4
\ end {array}\\
\
\ IIint_d dV &=&\ int_0^4\ int_ {y/2} ^ {2}\ int_0^ {1-x/2} dz\, dx\, dy &+&\ int_0^4\ int_ {0} ^ {y/2}\ int_0^ {1-y/4} dz\, dx\, dy
\ end {array}
\]
Los cuatro órdenes restantes de integración no requieren una suma de triples integrales. En la Figura 13.44 se muestra\(D\) colapsado sobre los otros dos planos de coordenadas. Mediante estas gráficas, damos aquí las órdenes finales de integración, dejando nuevamente al lector confirmar estos resultados.
\(dy \, dx \, dz\):
$$\ begin {array} {cc}
\ begin {array} {c}
0\ leq y\ leq 4-4z\\
0\ leq x\ leq 2-2z\\
0\ leq z\ leq 1
\ end {array}
&
\ Rightarrow\ int_0^1\ int_ {0} ^ {2-2z}\ int_0^ {4-4z} dy\, dx\, dz
\ end {array}
$$
\(dy dz dx\):
$$\ begin {array} {cc}
\ begin {array} {c}
0\ leq y\ leq 4-4z\\
0\ leq z\ leq 1-x/2\\
0\ leq x\ leq 2
\ end {array}
& ;
\ Rightarrow\ int_0^2\ int_ {0} ^ {1-x/2}\ int_0^ {4-4z} dy\, dx\, dz
\ end {array}
\]
\(dx \, dy \, dz\):
$$\ begin {array} {cc}
\ begin {array} {c}
0\ leq x\ leq 2-2z\\
0\ leq y\ leq 4-4z\\
0\ leq z\ leq 1
\ end {array}
&
\ Rightarrow\ int_0^1\ int_ {0} ^ {4-4z}\ int_0^ {2-2z} dx\, dy\, dz
\ end {array}
\]
\(dx \, dz \, dy\):
$$\ begin {array} {cc}
\ begin {array} {c}
0\ leq x\ leq 2-2z\\
0\ leq z\ leq 1-y/4\\
0\ leq y\ leq 4
\ end {array}
&
\ Rightarrow\ int_0^4\ int_ {0} ^ {1-y/4}\ int_0^ {2-2z} dx\, dz\, dy
\ end {array}
\]
Damos un ejemplo más de encontrar el volumen de una región espacial.
Ejemplo\(\PageIndex{6}\): Finding the volume of a space region
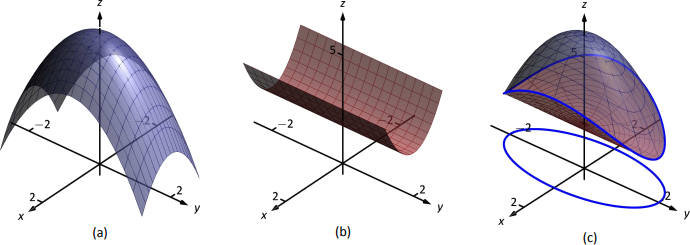
Configure una triple integral que dé el volumen de la región espacial\(D\) delimitada por\(z= 2x^2+2\) y\(z=6-2x^2-y^2\). Estas superficies están trazadas en la Figura 13.45 (a) y (b), respectivamente; la región\(D\) se muestra en la parte (c) de la figura.
Solución
El punto principal de este ejemplo es el siguiente: integrar con respecto a\(z\) primero es bastante sencillo; integrar con respecto a\(x\) primero no lo es.
El orden\(dz \, dy \, dx\):
Los límites en\(z\) son claramente\(2x^2+2\leq z\leq 6-2x^2-y^2\). Al colapsar\(D\) sobre el\(y\) plano\(x\) - se obtiene la elipse que se muestra en la Figura 13.45 (c). La ecuación de esta elipse se encuentra estableciendo las dos superficies iguales entre sí:
\[2x^2+2 = 6-2x^2-y^2\quad \Rightarrow\quad 4x^2+y^2=4\quad \Rightarrow\quad x^2+\frac{y^2}4=1.\]
Podemos describir esta elipse con los límites
\[-\sqrt{4-4x^2} \leq y\leq \sqrt{4-4x^2}\quad \text{and}\quad -1\leq x\leq 1.\]
Así encontramos volumen como
\ [\ begin {array} {cc}
\ begin {array} {c}
2x^2+2\ leq z\ leq 6-2x^2-y^2\\ [2pt]
-\ sqrt {4-4x^2}\ leq y\ leq\ sqrt {4-4x^2}\\ [2pt]
-1\ leq x\ leq 1
\ end {array}
&
\ Rightarrow\ int_ {-1} ^1\ int_ {-\ sqrt {4-4x^2}} ^ {\ sqrt {4-4x ^2}}\ int_ {2x^2+2} ^ {6-2x^2-y^2} dz\, dy\, dx
\ end {array}.
\]
El orden\(dy dz dx\):
Integrar con respecto a no\(y\) es demasiado difícil. Dado que la superficie\(z=2x^2+2\) es un cilindro cuya directriz es el\(y\) eje -eje, no crea un borde para\(y\). El paraboloide\(z=6-2x^2-y^2\) hace; resolviendo para\(y\), obtenemos los límites
\[-\sqrt{6-2x^2-z}\leq y\leq \sqrt{6-2x^2-z}.\]
Al colapsar\(D\) sobre los\(z\) ejes\(x\) - se obtiene la región que se muestra en la Figura 13.46 (a); la curva inferior es del cilindro, con ecuación\(z=2x^2+2\). La curva superior es del paraboloide; con\(y=0\), la curva es\(z=6-2x^2\). Así los límites\(z\) son\(2x^2+2\leq z\leq 6-2x^2\); los límites en\(x\) son\(-1\leq x\leq 1\). Así tenemos:
\ [\ begin {array} {cc}
\ begin {array} {c}
-\ sqrt {6-2x^2-z}\ leq y\ leq\ sqrt {6-2x^2-z}\\ [2pt]
2x^2+2\ leq z\ leq z\ leq 6-2x^2\ [2pt]
-1\ leq x\ leq 1
\ end {array}
&
\ Rightarrow\ int_ {-1} ^1\ int_ {2x^2+2} ^ {6-2x^2}\ int_ {-\ sqrt {6-2x^2-z}} ^ {\ sqrt {6-2x^2-z}} dy dz dx.
\ end {array}
\]
El orden\(dx \, dz \, dy\):
Este orden requiere más esfuerzo ya\(D\) que debe dividirse en dos subregiones. Las dos superficies crean dos conjuntos de límites superior/inferior en términos de\(x\); el cilindro crea límites $$-\ sqrt {z/2-1}\ leq x\ leq\ sqrt {z/2-1} $$ para región\(D_1\) y el paraboloide crea límites
\[-\sqrt{3-y^2/2-z^2/2}\leq x\leq \sqrt{3-y^2/2-z^2/2}\]
para la región\(D_2\).
Al colapsar\(D\) sobre los\(z\) ejes\(y\) - se obtienen las regiones que se muestran en la Figura 13.46 (b). Encontramos la ecuación de la curva\(z=4-y^2/2\) señalando que la ecuación de la elipse vista en la Figura 13.45 (c) tiene ecuación
\[x^2+y^2/4=1 \quad \Rightarrow \quad x = \sqrt{1-y^2/4}.\]
Sustituya esta expresión por\(x\) en cualquiera de las ecuaciones de superficie,\(z=6-2x^2-y^2\) o\(z=2x^2+2\). En ambos casos, encontramos
\[z=4-\frac12y^2.\]
Región\(R_1\), correspondiente a\(D_1\), tiene límites $$2\ leq z\ leq 4-y^2/2,\ quad -2\ leq y\ leq 2$$ y región\(R_2\), correspondiente a\(D_2\), tiene límites $$4-y^2/2\ leq z\ leq 6-y^2,\ quad -2\ leq y\ leq 2.$$ Así el volumen de\(D\) viene dado por:
$$\ int_ {-2} ^2\ int2\ _2^ {4-y^2/2}\ int_ {-\ sqrt {z/2-1}} ^ {\ sqrt {z/2-1}} dx\, dz\, dy\ +\ int_ {-2} ^2\ int_ {4-y^2/2} ^ {6-y^2}\ int_ {-\ sqrt {3-y^2/2-z^2/2}} ^ {\ sqrt {3-y^2/2-z^2/2} dx\, dz\, dy.\]
Si todo lo que uno quería hacer en el Ejemplo 13.6.6 era encontrar el volumen de la región\(D\), probablemente uno se hubiera detenido en la primera configuración de integración (con orden\(dz \, dy \, dx\)) y calculado el volumen a partir de ahí. Sin embargo, incluimos los otros dos métodos 1) para demostrar que podría hacerse, “desordenado” o no, y 2) porque a veces “tenemos” que usar un orden de integración menos deseable para poder integrarnos realmente.
Triple Integración y Funciones de Tres Variables
Hay usos para la triple integración más allá de simplemente encontrar volumen, así como hay usos para la integración más allá del “área bajo la curva”. Estos usos comienzan con la comprensión de cómo integrar funciones de tres variables, lo que efectivamente no es diferente a integrar funciones de dos variables. Esto nos lleva a una definición, seguida de un ejemplo.
Definición 107 Integración iterada, (Parte II)
Que\(D\) sea una región cerrada, acotada en el espacio, sobre la cual\(g_1(x)\)\(g_2(x)\),\(f_1(x,y)\),\(f_2(x,y)\) y\(h(x,y,z)\) son todos continuos, y dejar\(a\) y\(b\) ser números reales.
La integral iterada\( \int_a^b\int_{g_1(x)}^{g_2(x)}\int_{f_1(x,y)}^{f_2(x,y)} h(x,y,z) dz \, dy \, dx\) se evalúa como
$$\ int_a^b\ int_ {g_1 (x)} ^ {g_2 (x)}\ int_ {f_1 (x, y)} ^ {f_2 (x, y)} h (x, y, z) dz\, dy\, dx =\ int_a^b\ int_ {g_1 (x)} ^ {g_2 (x)}\ izquierda (\ int_ {f_1 (x, y)} ^ {f_2 (x, y)} h (x, y, z) dz\ derecha) dy\, dx.\]
Ejemplo\(\PageIndex{7}\): Evaluating a triple integral of a function of three variables
Evaluar\( \int_0^1\int_{x^2}^x\int_{x^2-y}^{2x+3y} \big(xy+2xz\big) dz \, dy \, dx.\)
Solución
Evaluamos esta integral de acuerdo con la Definición 107.
\( \int_0^1\int_{x^2}^x\int_{x^2-y}^{2x+3y} \big(xy+2xz\big) dz \, dy \, dx \)
\ (\ begin {align*}
&=\ int_0^1\ int_ {x^2} ^x\ izquierda (\ int_ {x^2-y} ^ {2x+3y}\ grande (xy+2xz\ grande) dz\ derecha) dy\, dx\
&=\ int_0^1\ int_ {x^2} ^x\ izquierda (\ grande (xyz+ z^2\ grande)\ Big|_ {x^2-y} ^ {2x+3y}\ derecha) dy\, dx\
&=\ int_0^1\ int_ {x^2} ^x\ Bigg (xy (2x+3y ) +x (2x+3y) ^2-\ Grande (xy (x^2-y) +x (x^2-y) ^2\ Grande)\ Bigg) dy\, dx\\
&=\ int_0^1\ int_ {x^2} ^x\ Grande (-x^5+x^3y+4x^3+14x^2y+12xy^2\ Grande), dx. \ end {align*}\)
Seguimos como lo hemos hecho en el pasado, mostrando menos pasos.
\ (\ begin {align*} &=\ int_0^1\ Bigg (-\ frac72x^7-8x^6-\ frac72x^5+15x^4\ Bigg) dx\\
&=\ frac {281} {336}\ aprox 0.836.
\ end {alinear*}\)
Ahora sabemos evaluar una triple integral de una función de tres variables; aún no entendemos lo que significa. Construimos este entendimiento de una manera muy similar a como hemos entendido la integración y la doble integración.
Dejar\(h(x,y,z)\) una función continua de tres variables, definidas sobre alguna región espacial\(D\). Podemos particionar\(D\) en subregiones\(n\) rectangulares-sólidas, cada una con dimensiones\(\Delta x_i\times\Delta y_i\times\Delta z_i\). Seamos\((x_i,y_i,z_i)\) algún punto en la\(i^{\,\text{th}}\) subregión, y consideremos el producto\(h(x_i,y_i,z_i)\Delta x_i\Delta y_i\Delta z_i\). Es el producto de un valor de función (esa es la\(h(x_i,y_i,z_i)\) parte) y un pequeño volumen\(\Delta V_i\) (esa es la\(\Delta x_i\Delta y_i\Delta z_i\) parte). Uno de los entendimientos más simples de este tipo de productos es cuando\(h\) describe la densidad de un objeto, para entonces\(h\times\text{volume}=\text{mass}\).
Podemos resumir todos los\(n\) productos\(D\). Nuevamente dejando\(||\Delta D||\) representar la longitud de la diagonal más larga de los sólidos\(n\) rectangulares en la partición, podemos tomar el límite de las sumas de productos como\(||\Delta D||\to 0\). Es decir, podemos encontrar
$$ S =\ lim_ {||\ Delta D||\ a 0}\ suma_ {i=1} ^n h (x_i, y_i, z_i)\ Delta v_i=\ lim_ {||\ Delta D||\ a 0}\ suma_ {i=1} ^n h (x_i, y_i, z_i)\ Delta x_i\ Delta y_i\ Delta z_i.\]
Si bien este límite tiene muchas interpretaciones dependiendo de la función\(h\), en el caso donde\(h\) describe densidad,\(S\) es la masa total del objeto descrito por la región\(D\).
Ahora usamos el límite anterior para definir la triple integral, dar un teorema que relaciona las triples integrales con la iteración iterada, seguido de la aplicación de las integrales triples para encontrar los centros de masa de los objetos sólidos.
Definición 108 Triple Integral
Dejar\(w=h(x,y,z)\) ser una función continua sobre una región de espacio cerrado y delimitado\(D\), y dejar\(\Delta D\) ser cualquier partición de\(D\) en sólidos\(n\) rectangulares con volumen\(\Delta V_i\). La triple integral de\(h\) over\(D\) es
$$\ IIint_dh (x, y, z) dV =\ lim_ {||\ Delta D||\ a 0}\ sum_ {i=1} ^n h (x_i, y_i, z_i)\ Delta v_i.\]
Nota: Anteriormente mostramos cómo la suma de rectángulos sobre una región\(R\) en el plano podría verse como una suma doble, conduciendo a la doble integral. Asimismo, podemos ver la suma\( \sum_{i=1}^nh(x_i,y_i,z_i)\Delta x_i\Delta y_i\Delta z_i\) como una suma triple, $$\ sum_ {k=1} ^p\ suma_ {j=1} ^n\ sum_ {i=1} ^mh (x_i, y_j, z_k)\ Delta x_i\ Delta y_j\ Delta z_k, $$ que evaluamos como
\[\sum_{k=1}^p\left(\sum_{j=1}^n\left(\sum_{i=1}^mh(x_i,y_j,z_k)\Delta x_i\right)\Delta y_j\right)\Delta z_k.\]
Aquí fijamos un\(k\) valor, que establece la\(z\) -altura de los sólidos rectangulares en un “nivel” de todos los sólidos rectangulares en la región espacial\(D\). La doble suma interna suma todos los volúmenes de los sólidos rectangulares en este nivel, mientras que la suma externa suma los volúmenes de cada nivel.
Esta comprensión de triple suma conduce a la\(\iiint_D\) notación de la triple integral, así como al método de evaluación mostrado en el Teorema 127.
El siguiente teorema nos asegura que el límite anterior existe para funciones continuas\(h\) y nos da un método de evaluación del límite.
teorema 127 Triple Integración (Parte II)
Dejar\(w=h(x,y,z)\) ser una función continua sobre una región de espacio cerrado y delimitado\(D\), y dejar\(\Delta D\) ser cualquier partición de\(D\) en sólidos\(n\) rectangulares con volumen\(V_i\).
- El límite\( \lim_{||\Delta D||\to 0}\sum_{i=1}^n h(x_i,y_i,z_i)\Delta V_i\) existe.
- Si\(D\) se define como la región delimitada por los planos\(x=a\) y\(x=b\), los cilindros\(y=g_1(x)\) y\(y=g_2(x)\), y las superficies\(z=f_1(x,y)\) y\(z=f_2(x,y)\), donde\(a<b\),\(g_1(x)\leq g_2(x)\) y\(f_1(x,y)\leq f_2(x,y)\) en\(D\), entonces
$$\ IIint_d h (x, y, z) dV =\ int_a^b\ int_ {g_1 (x )} ^ {g_2 (x)}\ int_ {f_1 (x, y)} ^ {f_2 (x, y)} h (x, y, z) dz\, dy\, dx. $$
Ahora aplicamos triple integración para encontrar los centros de masa de objetos sólidos.
Masa y Centro de Masa
Es posible que se desee revisar la Sección 13.4 para un recordatorio de los términos y conceptos pertinentes.
Definición 109 Masa, centro de masa de sólidos
Dejar que un sólido sea representado por una región\(D\) en el espacio con función de densidad variable\(\delta(x,y,z)\).
- La masa del objeto es\( M= \iiint_D \ dm=\iiint_D \delta(x,y,z) dV\).
- El momento sobre el\(x\) -\(y\) avión es\( M_{xy}=\iiint_D z\delta(x,y,z) dV\).
- El momento sobre el\(x\) -\(z\) avión es\( M_{xz}=\iiint_D y\delta(x,y,z) dV\).
- El momento sobre el\(y\) -\(z\) avión es\( M_{yz}=\iiint_D x\delta(x,y,z) dV\).
- El centro de masa del objeto es $$\ big (\ overline {x},\ overline {y},\ overline {z}\ big) =\ left (\ frac {M_ {yz}} M,\ frac {M_ {xz}} M,\ frac {M_ {xy}} M\ right) . $$
Ejemplo\(\PageIndex{8}\): Finding the center of mass of a solid
Encontrar la masa y el centro de masa del sólido representado por la región espacial delimitada por los planos de coordenadas y\(z=2-y/3-2x/3\), mostrado en la Figura 13.47, con densidad constante\(\delta(x,y,z)=3\) gm/cm\(^3\). (Nota: esta región espacial se utilizó en el Ejemplo 13.6.2.)
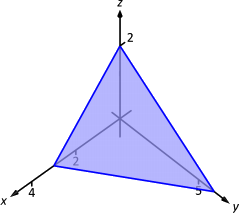
Solución
Aplicamos Definición 109. En el Ejemplo 13.6.2, encontramos límites para que el orden de integración\(dz \, dy \, dx\) sea\(0\leq z\leq 2-y/3-2x/3\),\(0\leq y\leq 6-2x\) y\(0\leq x\leq 3\). Encontramos la masa del objeto:
\ [\ begin {align*}
M &=\ IIint_d\ delta (x, y, z) dV\\
&=\ int_0^3\ int_0^ {6-2x}\ int_0^ {2-y/3-2x/3}\ big (3\ big) dz\, dy\, dx\
&= 3\ int_0^3\ int_0^ {6-2x} int_0^ {2-y/3-2x/3} dz\, dy\, dx\\
&= 3 (6) = 18\ texto {gm}.
\ end {alinear*}\]
La evaluación de la triple integral se realiza en el Ejemplo 13.6.2, por lo que nos saltamos esos pasos anteriores. Observe cómo la masa de un objeto con densidad constante es simplemente “\(\times\)volumen de densidad”.
Ahora nos encontramos con los momentos sobre los aviones.
\ [\ begin {align*}
M_ {xy} &=\ iiInt_d 3z dV\\
&=\ int_0^3\ int_0^ {6-2x}\ int_0^ {2-y/3-2x/3}\ grande (3z\ grande) dz\, dy\, dx\
%&=\ int_0^3\ int_0^ {6-2x}\ frac16\ grande (2x+y-6\ grande) ^2 dy\, dx\\
&=\ int_0^3\ int_0^ {6-2x}\ frac32\ grande (2-y/3-2x/3\ grande) ^2 dy\, dx\\
&=\ int_0^3 -\ frac49\ grande (x-3\ grande) ^3 dx\\
&= 9.
\ end {alinear*}\]
Omitimos los pasos de integrarnos para encontrar los otros momentos.
\ [\ begin {align*}
M_ {yz} &=\ iiInt_D 3x dV\\
&=\ frac {27} 2. \\
M_ {xz} &=\ IIint_D 3y dV\\
&= 27.
\ end {alinear*}\]
El centro de masa es $$\ big (\ overline {x},\ overline {y},\ overline {z}\ big) =\ left (\ frac {27/2} {18},\ frac {27} {18},\ frac {9} {18}\ right) =\ big (0.75,1.5,0.5\ big).\]
Ejemplo\(\PageIndex{9}\): Finding the center of mass of a solid
Encuentra el centro de masa del sólido representado por la región delimitada por los planos\(z=0\)\(z=-y\) y el cilindro\(x^2+y^2=1\), mostrado en la Figura 13.48, con función de densidad\(\delta(x,y,z) = 10+x^2+5y-5z\). (Nota: esta región espacial se utilizó en el Ejemplo 13.6.3.)
Solución
Al comenzar, consideremos la función de densidad. Es simétrico con respecto al\(y\)\(z\) plano, y cuanto más se mueve uno de este plano, más denso es el objeto. La simetría indica que\(\overline x\) debe ser 0.
A medida que uno se aleja del origen en las\(z\) direcciones\(y\) o, el objeto se vuelve menos denso, aunque hay más volumen en estas regiones.
Aunque ninguna de las integrales necesarias para calcular el centro de masa es particularmente difícil, requieren una serie de pasos. Destacamos aquí la importancia de saber configurar las integrales adecuadas; en situaciones complejas podemos apelar a la tecnología para una buena aproximación, si no la respuesta exacta. Utilizamos el orden de integración\(dz \, dy \, dx\), usando los límites que se encuentran en el Ejemplo 13.6.4. (Como estos son los mismos para las cuatro integrales triples, mostramos explícitamente los límites solo para\(M\).)
\ [\ begin {align*}
M &=\ iiInt_D\ grande (10+x^2+5y-5z\ grande) dV\\
&=\ int_ {-1} ^1\ int_ {-\ sqrt {1-x^2}} ^0\ int_0^ {-y}\ grande (10+x^2+5y-5z\ grande) dV\
&=\ frac 64} 5-\ frac {15\ pi} {16}\ aprox 3.855. \\
M_ {yz} &=\ iiInt_D x\ grande (10+x^2+5y-5z\ grande) dV\\ %& M_ {xy} &=\ iiInt_D z\ grande (10+x^2+5y-5z\ grande) dV y M_ {xz}\\
&=0. \\
M_ {xz} &=\ IIint_D y\ grande (10+x^2+5y-5z\ grande) dV\\
&= 2-\ frac {61\ pi} {48}\ aprox. -1.99. \\
M_ {xy} &=\ iiInt_d z\ grande (10+x^2+5y-5z\ grande) dV\\
&=\ frac {61\ pi} {96} -\ frac {10} 9\ aprox 0.885.
\ end {align*}\]
Observe cómo\(M_{yz}=0\), como se esperaba. El centro de masa es
$$\ grande (\ overline {x},\ overline {y},\ overline {z}\ grande) =\ izquierda (0,\ frac {-1.99} {3.855},\ frac {0.885} {3.855}\ derecha)\ approx\ grande (0, -0.516, 0.230\ grande).\]
Como se indicó anteriormente, hay muchos usos para la triple integración más allá de encontrar volumen. Cuando\(h(x,y,z)\) describe una función de tasa de cambio sobre alguna región espacial\(D\), luego\( \iiint_D h(x,y,z) dV\) da el cambio total sobre\(D\). Nuestro ejemplo específico de esto fue calcular la masa; una función de densidad es simplemente una función de “tasa de cambio de masa por volumen”. La densidad integradora da masa total.
Si bien saber cómo integrar es importante, podría decirse que es mucho más importante saber cómo configurar integrales. Se necesita habilidad para crear una fórmula que describa una cantidad deseada; la tecnología moderna es muy útil para evaluar estas fórmulas de manera rápida y precisa.
Este capítulo investigó el seguimiento natural de las derivadas parciales: la integración iterada. Aprendimos a usar los límites de una doble integral para describir una región en el plano usando coordenadas rectangulares y polares, luego expandimos para usar los límites de una triple integral para describir una región en el espacio. Utilizamos integrales dobles para encontrar volúmenes bajo superficies, área superficial y centro de masa de lámina; utilizamos integrales triples como método alternativo para encontrar volúmenes de regiones espaciales y también para encontrar el centro de masa de una región en el espacio.
La integración no se detiene aquí. Podríamos continuar iterando nuestras integrales, investigando a continuación “integrales cuádruples” cuyos límites describen una región en el espacio 4—dimensional (que son muy difíciles de visualizar). También podemos mirar hacia atrás a la integración “regular” donde encontramos el área bajo una curva en el plano. Un análogo natural a esto es encontrar el “área bajo una curva”, donde la curva está en el espacio, no en un plano. Estas son solo dos de las muchas vías para explorar bajo el epígrafe de “integración”.