15.4: Integrales triples
- Page ID
- 116265
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Reconocer cuando una función de tres variables es integrable sobre una caja rectangular.
- Evaluar una triple integral expresándola como una integral iterada.
- Reconocer cuando una función de tres variables es integrable sobre una región cerrada y delimitada.
- Simplifique un cálculo cambiando el orden de integración de una triple integral.
- Calcular el valor promedio de una función de tres variables.
Anteriormente, discutimos la doble integral de una función\(f(x,y)\) de dos variables sobre una región rectangular en el plano. En esta sección definimos la triple integral de una función\(f(x,y,z)\) de tres variables sobre una caja sólida rectangular en el espacio,\(\mathbb{R}^3\). Posteriormente en esta sección extendemos la definición a regiones más generales en\(\mathbb{R}^3\).
Funciones integrables de tres variables
Podemos definir una caja rectangular\(B\) en\(\mathbb{R}^3\) como
\[B = \big\{(x,y,z)\,|\,a \leq x \leq b, \, c \leq y \leq d, \, e \leq z \leq f \big\}. \nonumber \]
Seguimos un procedimiento similar al que hicimos anteriormente. Dividimos el intervalo\([a,b]\) en\(l\) subintervalos\([x_{i-1},x_i]\) de igual longitud\(\Delta x\) con
\[\Delta x = \dfrac{x_i - x_{i-1}}{l}, \nonumber \]
dividir el intervalo\([c,d]\) en\(m\) subintervalos\([y_{i-1}, y_i]\) de igual longitud\(\Delta y\) con
\[\Delta y = \dfrac{y_j - y_{j-1}}{m}, \nonumber \]
y dividir el intervalo\([e,f]\) en\(n\) subintervalos\([z_{i-1},z_i]\) de igual longitud\(\Delta z\) con
\[\Delta z = \dfrac{z_k - z_{k-1}}{n} \nonumber \]
Entonces la caja rectangular\(B\) se subdivide en\(lmn\) subcajas:
\[B_{ijk} = [x_{i-1}, x_i] \times [y_{i-1}, y_i] \times [z_{i-1},z_i], \nonumber \]
como se muestra en la Figura\(\PageIndex{1}\).
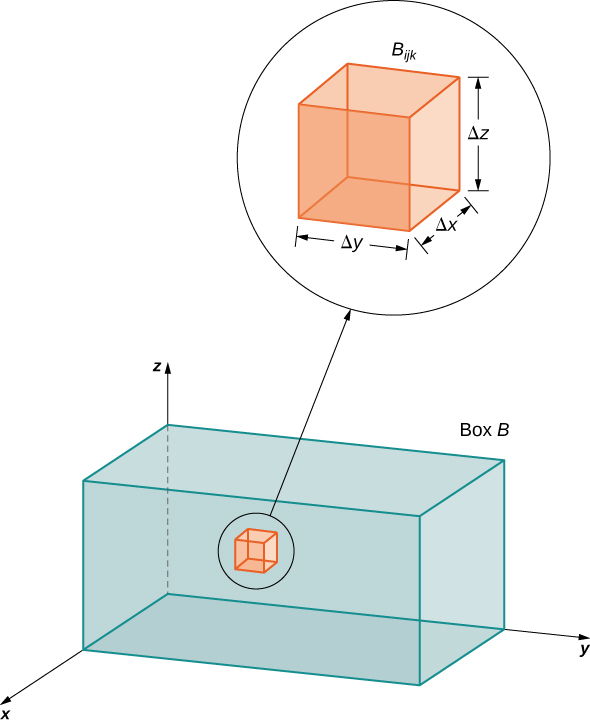
Para cada uno\(i, \, j,\) y\(k\), considere un punto de muestra\((x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\) en cada sub-caja\(B_{ijk}\). Vemos que su volumen es\(\Delta V = \Delta x \Delta y \Delta z\). Formar la suma triple de Riemann
\[\sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f ( x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\,\Delta x \Delta y \Delta z. \nonumber \]
Definimos la triple integral en términos del límite de una suma triple de Riemann, como hicimos para la doble integral en términos de una doble suma de Riemann.
La triple integral de una función\(f(x,y,z)\) sobre una caja rectangular\(B\) se define como
\[\lim_{l,m,n\rightarrow\infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f ( x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\,\Delta x \Delta y \Delta z = \iiint_B f(x,y,z) \,dV \nonumber \]si existe este límite.
Cuando la triple integral existe en\(B\) la función\(f(x,y,z)\) se dice que es integrable en\(B\). Además, la triple integral existe si\(f(x,y,z)\) es continua en\(B\). Por lo tanto, utilizaremos funciones continuas para nuestros ejemplos. Sin embargo, la continuidad es suficiente pero no necesaria; en otras palabras,\(f\) está limitada\(B\) y continua excepto posiblemente en el límite de\(B\). El punto de muestreo\((x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\) puede ser cualquier punto de la sub-caja rectangular\(B_{ijk}\) y todas las propiedades de una doble integral se aplican a una triple integral. Así como la doble integral tiene muchas aplicaciones prácticas, la triple integral también tiene muchas aplicaciones, que discutimos en secciones posteriores.
Ahora que hemos desarrollado el concepto de la triple integral, necesitamos saber cómo computarlo. Así como en el caso de la doble integral, podemos tener una triple integral iterada, y en consecuencia, existe una versión del teorema de Fubini para triples integrales.
Si\(f(x,y,z)\) es continuo en una caja rectangular\(B = [a,b] \times [c,d] \times [e,f]\), entonces
\[\iint_B f(x,y,z) \,dV = \int_e^f \int_c^d \int_a^b f(x,y,z) \,dx \, dy \, dz. \nonumber \]
Esta integral también es igual a cualquiera de los otros cinco ordenamientos posibles para la triple integral iterada.
Para\(a, b, c, d, e\) y números\(f\) reales, la triple integral iterada se puede expresar en seis ordenamientos diferentes:
\[\begin{align} \int_e^f \int_c^d \int_a^b f(x,y,z)\, dx \, dy \, dz = \int_e^f \left( \int_c^d \left( \int_a^b f(x,y,z) \,dx \right) dy \right) dz \\ = \int_c^d \left( \int_e^f \left( \int_a^b f(x,y,z) \,dx \right)dz \right) dy \\ = \int_a^b \left( \int_e^f \left( \int_c^d f(x,y,z) \,dy \right)dz \right) dx \\ = \int_e^f \left( \int_a^b \left( \int_c^d f(x,y,z) \,dy \right) dx \right) dz \\ = \int_c^d \left( \int_a^b \left( \int_c^d f(x,y,z) \,dz\right)dx \right) dy \\ = \int_a^b \left( \int_c^d \left( \int_e^f f(x,y,z) \,dz \right) dy \right) dx \end{align} \nonumber \]
Para una caja rectangular, el orden de integración no hace ninguna diferencia significativa en el nivel de dificultad en el cálculo. Calculamos integrales triples usando el Teorema de Fubini en lugar de usar la definición de suma de Riemann. Seguimos el orden de integración de la misma manera que lo hicimos para las dobles integrales (es decir, de adentro a afuera).
Evaluar la triple integral\[\int_{z=0}^{z=1} \int_{y=2}^{y=4} \int_{x=-1}^{x=5} (x + yz^2)\, dx \, dy \, dz. \nonumber \]
Solución
El orden de integración se especifica en el problema, así integrar con respecto a\(x\) primero, luego y, y luego\(z\).
\[\begin{align*}&\int_{z=0}^{z=1} \int_{y=2}^{y=4} \int_{x=-1}^{x=5} (x + yz^2) \,dx \,dy \,dz \\ &= \int_{z=0}^{z=1} \int_{y=2}^{y=4} \left. \left[ \dfrac{x^2}{2} + xyz^2\right|_{x=-1}^{x=5}\right]\,dy \,dz &&\text{Integrate with respect to $x$.}\\ &= \int_{z=0}^{z=1} \int_{y=2}^{y=4} \left[12+6yz^2\right] \,dy \,dz &&\text{Evaluate.}\\ &= \int_{z=0}^{z=1} \left[ \left.12y+6\dfrac{y^2}{2}z^2 \right|_{y=2}^{y=4} \right] dz &&\text{Integrate with respect to $y$.} \\ &= \int_{z=0}^{z=1} [24+36z^2] \, dz &&\text{Evaluate.} \\ &= \left[ 24z+36\dfrac{z^3}{3} \right]_{z=0}^{z=1} &&\text{Integrate with respect to $z$.}\\ &=36. &&\text{Evaluate.}\end{align*}\]
Evaluar la triple integral
\[\iiint_B x^2 yz \,dV \nonumber \]
donde\(B = \big\{(x,y,z)\,|\, - 2 \leq x \leq 1, \, 0 \leq y \leq 3, \, 1 \leq z \leq 5 \big\} \) como se muestra en la Figura\(\PageIndex{2}\).
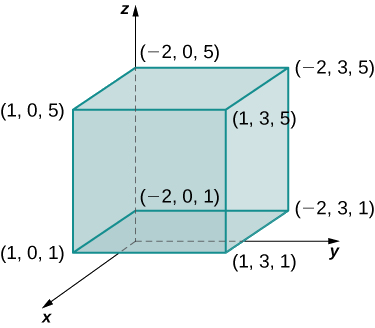
Solución
No se especifica el orden, pero podemos usar la integral iterada en cualquier orden sin cambiar el nivel de dificultad. Elige, digamos, integrar\(y\) primero, luego\(x\), y luego\(z\).
\[\begin{align*}\iiint\limits_{B} x^2 yz \,dV &= \int_1^5 \int_{-2}^1 \int_0^3 [x^2 yz] \,dy \, dx \, dz \\&= \int_1^5 \int_{-2}^1 \left[ \left. x^2 \dfrac{y^3}{3} z\right|_0^3 \right] dx \, dz \\&= \int_1^5 \int_{-2}^1 \dfrac{y}{2} x^2 z \,dx \, dz \\&= \int_1^5 \left[ \left. \dfrac{9}{2} \dfrac{x^3}{3} z \right|_{-2}^1 \right] dz \\&= \int_1^5 \dfrac{27}{2} z \, dz \\&= \left. \dfrac{27}{2} \dfrac{z^2}{2} \right|_1^5 = 162.\end{align*}\]
Ahora intenta integrarte en un orden diferente solo para ver que obtenemos la misma respuesta. Elegir integrar con respecto a\(x\) primero, luego\(z\), luego\(y\)
\[\begin{align*}\iiint\limits_{B} x^2yz \,dV &= \int_0^3 \int_1^5 \int_{-2}^1 [x^2yz] \,dx\, dz\, dy \\&= \int_0^3 \int_1^5 \left[ \left. \dfrac{x^3}{3} yz \right|_{-2}^1 \right] dz \,dy \\&= \int_0^3 \int_1^5 3yz \; dz \,dy \\&= \int_0^3 \left.\left[ 3y\dfrac{z^2}{2} \right|_1^5 \right] \,dy \\&= \int_0^3 36y \; dy \\&= \left. 36\dfrac{y^2}{2} \right|_0^3 =18(9-0) =162.\end{align*}\]
Evaluar la triple integral
\[\iiint_B z \, \sin \, x \, \cos \, y \, dV\nonumber \]
donde\(B = \big\{(x,y,z)\,|\,0 \leq x \leq \pi, \, \dfrac{3\pi}{2} \leq y \leq 2\pi, \, 1 \leq z \leq 3 \big\}\).
- Pista
-
Sigue los pasos del ejemplo anterior.
- Contestar
-
\[\iiint_B z \, \sin \, x \, \cos \, y \, dV = 8 \nonumber \]
La triple integral de una función continua\(f(x,y,z)\) sobre una región tridimensional general
\[E = \big\{(x,y,z)\,|\,(x,y) \in D, \, u_1(x,y) \leq z \leq u_2(x,y) \big\} \nonumber \]
en\(\mathbb{R}^3\), donde\(D\) esta la proyeccion de\(E\) sobre el\(xy\) -plano, es
\[\iiint_E f(x,y,z) \,dV = \iint_D \left[\int_{u_1(x,y)}^{u_2(x,y)} f(x,y,z) \,dz \right] \, dA. \nonumber \]
De igual manera, podemos considerar una región delimitada general\(D\) en el\(xy\) -plano y dos funciones\(y = u_1(x,z)\) y\(y = u_2(x,z)\) tal que\(u_1(x,z) \leq u_2(x,z)\) para todos\((x,z)\) en\(D\). Luego podemos describir la región sólida\(E\) en\(\mathbb{R}^3\) como
\[E = \big\{(x,y,z)\,|\,(x,z) \in D, \, u_1(x,z) \leq z \leq u_2(x,z) \big\} \nonumber \]donde\(D\) esta la proyeccion de\(E\) sobre el\(xy\) plano y la triple integral es
\[\iiint_E f(x,y,z)\,dV = \iint_D \left[\int_{u_1(x,z)}^{u_2(x,z)} f(x,y,z) \,dy \right] \, dA. \nonumber \]
Finalmente, si\(D\) es una región delimitada general en el\(xy\) plano -y tenemos dos funciones\(x = u_1(y,z)\) y\(x = u_2(y,z)\) tal que\(u_1(y,z) \leq u_2(y,z)\) para todos\((y,z)\) adentro\(D\), entonces la región sólida\(E\) en\(\mathbb{R}^3\) puede describirse como
\[E = \big\{(x,y,z)\,|\,(y,z) \in D, \, u_1(y,z) \leq z \leq u_2(y,z) \big\} \nonumber \]donde\(D\) esta la proyeccion de\(E\) sobre el\(xy\) plano y la triple integral es
\[\iiint_E f(x,y,z)\,dV = \iint_D \left[\int_{u_1(y,z)}^{u_2(y,z)} f(x,y,z) \, dx \right] \, dA. \nonumber \]
Tenga en cuenta que la región\(D\) en cualquiera de los planos puede ser de Tipo I o Tipo II como se describe anteriormente. Si\(D\) en el\(xy\) plano -es de Tipo I (Figura\(\PageIndex{4}\)), entonces
\[E = \big\{(x,y,z)\,|\,a \leq x \leq b, \, g_1(x) \leq y \leq g_2(x), \, u_1(x,y) \leq z \leq u_2(x,y) \big\}. \nonumber \]
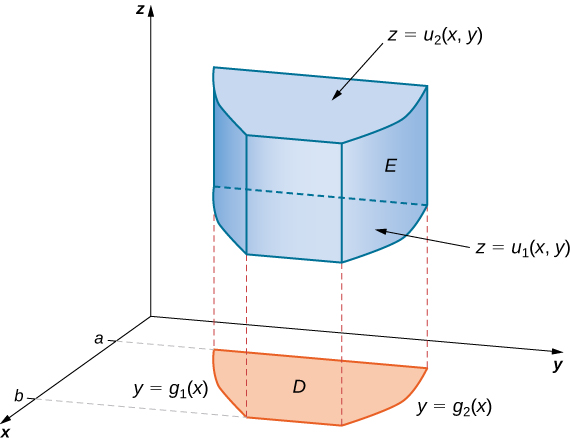
Entonces la triple integral se convierte
\[\iiint_E f(x,y,z) \,dV = \int_a^b \int_{g_1(x)}^{g_2(x)} \int_{u_1(x,y)}^{u_2(x,y)} f(x,y,z) \,dz \, dy \, dx. \nonumber \]
Si\(D\) en el\(xy\) plano -es de Tipo II (Figura\(\PageIndex{5}\)), entonces
\[E = \big\{(x,y,z)\,|\,c \leq x \leq d, h_1(x) \leq y \leq h_2(x), \, u_1(x,y) \leq z \leq u_2(x,y) \big\}. \nonumber \]
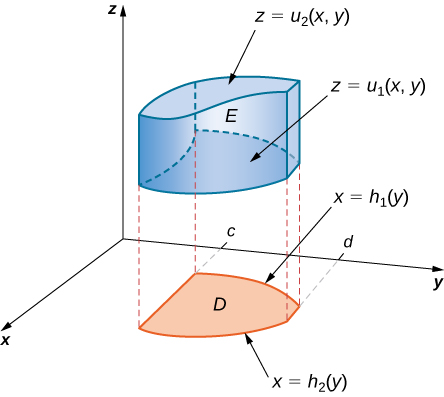
Entonces la triple integral se convierte
\[\iiint_E f(x,y,z) \,dV = \int_{y=c}^{y=d} \int_{x=h_1(y)}^{x=h_2(y)} \int_{z=u_1(x,y)}^{z=u_2(x,y)} f(x,y,z)\,dz \, dx \, dy. \nonumber \]
Evaluar la triple integral de la función\(f(x,y,z) = 5x - 3y\) sobre el tetraedro sólido delimitado por los planos\(x = 0, \, y = 0, \, z = 0\), y\(x + y + z = 1\).
Solución
La figura\(\PageIndex{6}\) muestra el tetraedro sólido\(E\) y su proyección\(D\) en el\(xy\) plano.
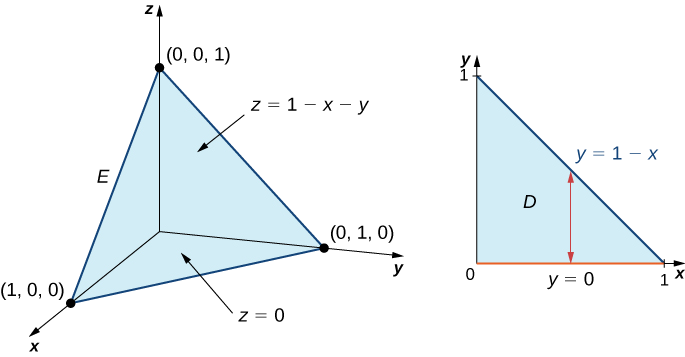
Podemos describir el tetraedro de región sólida como
\[E = \big\{(x,y,z)\,|\,0 \leq x \leq 1, \, 0 \leq y \leq 1 - x, \, 0 \leq z \leq 1 - x - y \big\}. \nonumber \]
De ahí que la triple integral sea
\[\iiint_E f(x,y,z) \,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y} (5x - 3y) \,dz \, dy \, dx. \nonumber \]
Para simplificar el cálculo, primero evalúe la integral\(\displaystyle \int_{z=0}^{z=1-x-y} (5x - 3y) \,dz\). Tenemos
\[\int_{z=0}^{z=1-x-y} (5x - 3y) \,dz = (5x - 3y)z \bigg|_{z=0}^{z=1-x-y} = (5x - 3y)(1 - x - y).\nonumber \]
Ahora evalúe la integral
\[\int_{y=0}^{y=1-x} (5x - 3y)(1 - x - y) \,dy, \nonumber \]
obteniendo
\[\int_{y=0}^{y=1-x} (5x - 3y)(1 - x - y)\,dy = \dfrac{1}{2}(x - 1)^2 (6x - 1).\nonumber \]
Finalmente evaluar
\[\int_{x=0}^{x=1} \dfrac{1}{2}(x - 1)^2 (6x - 1)\,dx = \dfrac{1}{12}.\nonumber \]
Poniéndolo todo junto, tenemos
\[\iiint_E f(x,y,z)\,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y}(5x - 3y)\,dz \, dy \, dx = \dfrac{1}{12}.\nonumber \]
Así como usamos la doble integral\[\iint_D 1 \,dA \nonumber \] para encontrar el área de una región delimitada general,\(D\) podemos usar\[\iiint_E 1\,dV \nonumber \] para encontrar el volumen de una región delimitada sólida general\(E\). El siguiente ejemplo ilustra el método.
Encuentra el volumen de una pirámide derecha que tiene la base cuadrada en el\(xy\) plano\([-1,1] \times [-1,1]\) y el vértice en el punto\((0, 0, 1)\) como se muestra en la siguiente figura.
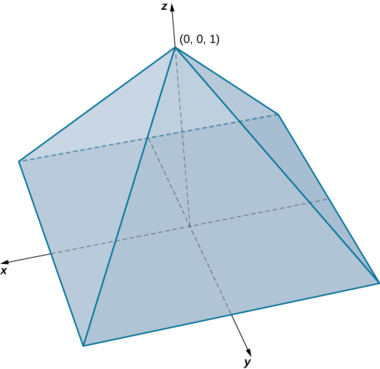
Solución
En esta pirámide el valor de\(z\) los cambios de 0 a 1 y a cada altura\(z\) la sección transversal de la pirámide para cualquier valor de\(z\) es el cuadrado
\[[-1 + z, \, 1 - z] \times [-1 + z, \, 1 - z].\nonumber \]
De ahí que el volumen de la pirámide sea\[\iiint_E 1\,dV\nonumber \] donde
\[E = \big\{(x,y,z)\,|\,0 \leq z \leq 1, \, -1 + z \leq y \leq 1 - z, \, -1 + z \leq x \leq 1 - z \big\}.\nonumber \]
Así, tenemos
\ [\ begin {alinear*}\ IIint_E 1\, dV &=\ int_ {z=0} ^ {z=1}\ int_ {y=-1+z} ^ {y=1-z}\ int_ {x=-1+z} ^ {x=1-z} 1\, dx\, dy\, dz\\ [5pt]
&=\ int_ {z=0} ^ {z=1}\ int_ {y=-1+z} ^ {y=1-z} (2 - 2z)\, dy\, dz\\ [5pt]
&=\ int_ {z=0} ^ {z=1} (2 - 2z) ^2\, dz =\ dfrac {4} {3}. \ end {alinear*}\]
De ahí que el volumen de la pirámide sea unidades\(\dfrac{4}{3}\) cúbicas.
Considera la esfera sólida\(E = \big\{(x,y,z)\,|\,x^2 + y^2 + z^2 = 9 \big\}\). Escribe la triple integral\[\iiint_E f(x,y,z) \,dV\nonumber \] para una función arbitraria\(f\) como una integral iterada. Después evaluar esta triple integral con\(f(x,y,z) = 1\). Observe que esto da el volumen de una esfera utilizando una triple integral.
- Pista
-
Sigue los pasos del ejemplo anterior. Usa simetría.
- Contestar
-
\[\begin{align*} \iiint_E 1\,dV = 8 \int_{x=-3}^{x=3} \int_{y=-\sqrt{9-z^2}}^{y=\sqrt{9-z^2}}\int_{z=-\sqrt{9-x^2-y^2}}^{z=\sqrt{9-x^2-y^2}} 1\,dz \, dy \, dx \\ = 36 \pi \,\text{cubic units}. \end{align*}\]
Cambiando el orden de integración
Como ya hemos visto en las dobles integrales sobre regiones delimitadas generales, cambiar el orden de la integración se hace con bastante frecuencia para simplificar el cálculo. Con una triple integral sobre una caja rectangular, el orden de integración no cambia el nivel de dificultad del cálculo. Sin embargo, con una triple integral sobre una región delimitada general, elegir un orden apropiado de integración puede simplificar bastante el cálculo. A veces hacer el cambio a las coordenadas polares también puede ser muy útil. Aquí demostramos dos ejemplos.
Considere la integral iterada
\[\int_{x=0}^{x=1} \int_{y=0}^{y=x^2} \int_{z=0}^{z=y} f(x,y,z)\,dz \, dy \, dx. \nonumber \]
El orden de integración aquí es primero con respecto a z, luego y, y luego x. Expresar esta integral cambiando el orden de integración para ser primero con respecto a\(x\), luego\(z\), y luego\(y\). Verificar que el valor de la integral sea el mismo si lo dejamos\(f (x,y,z) =xyz\).
Solución
La mejor manera de hacerlo es bosquejar la región\(E\) y sus proyecciones en cada uno de los tres planos de coordenadas. Por lo tanto, vamos
\[E = \big\{(x,y,z)\,|\,0 \leq x \leq 1, \, 0 \leq y \leq x^2, \, 0 \leq z \leq y \big\}.\nonumber \]
y
\[\int_{x=0}^{x=1} \int_{y=0}^{y=x^2} \int_{z=0}^{z=x^2} f(x,y,z) \,dz \, dy \, dx = \iiint_E f(x,y,z)\,dV.\nonumber \]
Necesitamos expresar esta triple integral como
\[\int_{y=c}^{y=d} \int_{z=v_1(y)}^{z=v_2(y)} \int_{x=u_1(y,z)}^{x=u_2(y,z)} f(x,y,z)\,dx \, dz \, dy.\nonumber \]
Conociendo la región\(E\) podemos dibujar las siguientes proyecciones (Figura\(\PageIndex{8}\)):
en el\(xy\) plano -es\(D_1 = \big\{(x,y)\,|\, 0 \leq x \leq 1, \, 0 \leq y \leq x^2 \big\} = \{ (x,y) \,|\, 0 \leq y \leq 1, \, \sqrt{y} \leq x \leq 1 \big\},\)
en el\(yz\) -avión es\(D_2 = \big\{(y,z) \,|\, 0 \leq y \leq 1, \, 0 \leq z \leq y^2 \big\}\), y
en el\(xz\) -avión es\(D_3 = \big\{(x,z) \,|\, 0 \leq x \leq 1, \, 0 \leq z \leq x^2 \big\}\).
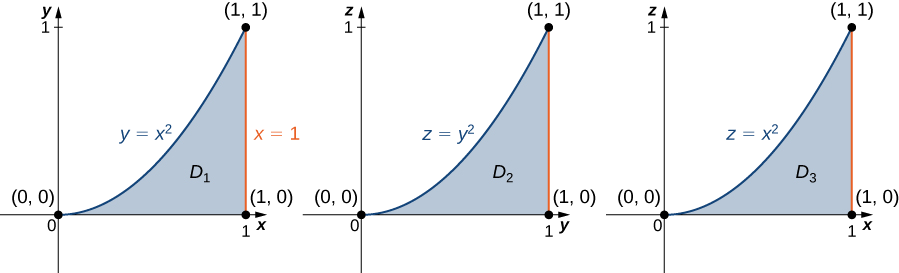
Ahora podemos describir la misma región en la\(E\) que\(\big\{(x,y,z) \,|\, 0 \leq y \leq 1, \, 0 \leq z \leq y^2, \, \sqrt{y} \leq x \leq 1 \big\}\), y consecuentemente, la triple integral se convierte
\[\int_{y=c}^{y=d} \int_{z=v_1(y)}^{z=v_2(y)} \int_{x=u_1(y,z)}^{x=u_2(y,z)} f(x,y,z)\,dx \, dz \, dy = \int_{y=0}^{y=1} \int_{z=0}^{z=x^2} \int_{x=\sqrt{y}}^{x=1} f(x,y,z)\,dx \, dz \, dy \nonumber \]
Ahora supongamos que\(f (x,y,z) = xyz\) en cada una de las integrales. Entonces tenemos
\ [\ begin {alinear*}\ int_ {x=0} ^ {x=1}\ int_ {y=0} ^ {y=x^2}\ int_ {z=0} ^ {z=y^2} xyz\, dz\, dy\, dx &=\ int_ {x=0} ^ {x=1}\ int_ {y=0} ^ {y=x^2}\ izquierda. \ izquierda [xy\ dfrac {z^2} {2}\ derecha|_ {z=0} ^ {z=y^2}\ derecha]\, dy\, dx\ [5pt]
&=\ int_ {x=0} ^ {x=1}\ int_ {y=0} ^ {y=x^2}\ izquierda (x\ dfrac {y^5} {2}}\ derecha) dy\, dx\\ [5pt]
&=\ int_ {x=0} ^ {x=1}\ izquierda. \ izquierda [x\ dfrac {y^6} {12}\ derecha|_ {y=0} ^ {y=x^2}\ derecha] dx\\ [5pt]
&=\ int_ {x=0} ^ {x=1}\ dfrac {x^ {13}} {12} dx =\ izquierda. \ dfrac {x^ {14}} {168}\ derecha|_ {x=0} ^ {x=1}\\ [5pt]
&=\ dfrac {1} {168},\ final {alinear*}\]
\ [\ begin {alinear*}\ int_ {y=0} ^ {y=1}\ int_ {z=0} ^ {z=y^2}\ int_ {x=\ sqrt {y}} ^ {x=1} xyz\, dx\, dz\, dy &=\ int_ {y=0} ^ {y=0} ^ {y=1}\ int_ {z=0} ^ {zy=0} ^2}\ izquierda. \ izquierda [yz\ dfrac {x^2} {2}\ derecha|_ {\ sqrt {y}} ^ {1}\ derecha] dz\, dy\ [5pt]
&=\ int_ {y=0} ^ {y=1}\ int_ {z=0} ^ {z=y^2}\ izquierda (\ dfrac {yz} {2} -\ dfrac {y^2z} {2}\ derecha) dz\, dy\\ [5pt]
&=\ int_ {y=0} ^ {y=1}\ izquierda. \ izquierda [\ dfrac {yz^2} {4} -\ dfrac {y^2z^2} {4}\ derecha|_ {z=0} ^ {z=y^2}\ derecha] dy\\ [5pt]
&=\ int_ {y=0} ^ {y=1}\ izquierda (\ dfrac {y^5} {4} -\ dfrac {y^6} {4}\ derecha) dy\\ [5pt]
&=\ izquierda. \ izquierda (\ dfrac {y^6} {24} -\ dfrac {y^7} {28}\ derecha)\ derecha|_ {y=0} ^ {y=1}\\ [5pt]
&=\ dfrac {1} {168}. \ end {align*}\ nonumber\]
Las respuestas coinciden.
Escribir cinco integrales iteradas diferentes iguales a la integral dada
\[\int_{z=0}^{z=4} \int_{y=0}^{y=4-z} \int_{x=0}^{x=\sqrt{y}} f(x,y,z) \, dx \, dy \, dz.\nonumber \]
- Pista
-
Siga los pasos del ejemplo anterior, utilizando la región\(E\) como\( \big\{(x,y,z) \,|\, 0 \leq z \leq 4, \, 0 \leq y \leq 4 - z, \, 0 \leq x \leq \sqrt{y} \big\}\), y describa y esboce las proyecciones en cada uno de los tres planos, cinco veces diferentes.
- Contestar
-
\[(i) \, \int_{z=0}^{z=4} \int_{x=0}^{x=\sqrt{4-z}} \int_{y=x^2}^{y=4-z} f(x,y,z) \, dy \, dx \, dz, \, (ii) \, \int_{y=0}^{y=4} \int_{z=0}^{z=4-y} \int_{x=0}^{x=\sqrt{y}} f(x,y,z) \,dx \, dz \, dy, \,(iii) \, \int_{y=0}^{y=4} \int_{x=0}^{x=\sqrt{y}} \int_{z=0}^{Z=4-y} f(x,y,z) \,dz \, dx \, dy, \, \nonumber \]
\[ (iv) \, \int_{x=0}^{x=2} \int_{y=x^2}^{y=4} \int_{z=0}^{z=4-y} f(x,y,z) \,dz \, dy \, dx, \, (v) \int_{x=0}^{x=2} \int_{z=0}^{z=4-x^2} \int_{y=x^2}^{y=4-z} f(x,y,z) \,dy \, dz \, dx \nonumber \]
Evaluar la triple integral
\[\iiint_{E} \sqrt{x^2 + z^2} \,dV, \nonumber \]
donde\(E\) está la región delimitada por el paraboloide\(y = x^2 + z^2\) (Figura\(\PageIndex{9}\)) y el plano\(y = 4\).
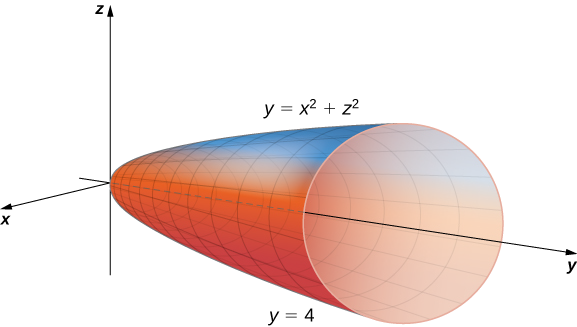
Solución
La proyección de la región sólida\(E\) sobre el\(xy\) plano es la región delimitada arriba\(y = 4\) y abajo por la parábola\(y = x^2\) como se muestra.
Así, tenemos
\[E = \big\{(x,y,z) \,|\, -2 \leq x \leq 2, \, x^2 \leq y \leq 4, \, -\sqrt{y - x^2} \leq z \sqrt{y - x^2} \big\}.\nonumber \]
La triple integral se convierte
\[\iiint_E \sqrt{x^2 + z^2} \,dV = \int_{x=-2}^{x=2} \int_{y=x^2}^{y=4} \int_{z=-\sqrt{y-x^2}}^{z=\sqrt{y-x^2}} \sqrt{x^2 + z^2} \,dz \, dy \, dx.\nonumber \]
Esta expresión es difícil de calcular, así que considere la proyección de\(E\) sobre el\(xz\) plano. Se trata de un disco circular\(x^2 + z^2 \leq 4\). Así obtenemos
\[\iiint_E \sqrt{x^2 + z^2} \,dV = \int_{x=-2}^{x=2} \int_{y=x^2}^{y=4} \int_{z=-\sqrt{y-x^2}}^{z=\sqrt{y-x^2}} \sqrt{x^2 + z^2} \,dz \, dy \, dx = \int_{x=-2}^{x=2} \int_{z=-\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} \int_{y=x^2+z^2}^{y=4} \sqrt{x^2 + z^2} \,dy \, dz \, dx.\nonumber \]
Aquí el orden de integración cambia de ser primero con respecto a\(z\) entonces\(y\) y luego\(x\) a ser primero con respecto a\(y\) entonces a\(z\) y luego a\(x\). Pronto quedará claro cómo este cambio puede ser beneficioso para el cálculo. Tenemos
\[\int_{x=-2}^{x=2} \int_{z=\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} \int_{y=x^2+z^2}^{y=4} \sqrt{x^2 + z^2} \,dy \, dz \, dx = \int_{x=-2}^{x=2} \int_{z=-\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} (4 - x^2 - z^2) \sqrt{x^2 + z^2} \,dz \, dx.\nonumber \]
Ahora usa la sustitución polar\(x = r \, \cos \, \theta, \, z = r \, \sin \, \theta\), y\(dz \, dx = r \, dr \, d\theta\) en el\(xz\) plano -. Esto es esencialmente lo mismo que cuando usamos coordenadas polares en el\(xy\) -plano, excepto que estamos reemplazando\(y\) por\(z\). En consecuencia los límites de la integración cambian y tenemos, al utilizar\(r^2 = x^2 + z^2\),
\[\int_{x=-2}^{x=2} \int_{z=-\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} (4 - x^2 - z^2) \sqrt{x^2 + z^2}\,dz \, dx = \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=2} (4 - r^2) rr \, dr \, d\theta = \int_0^{2\pi} \left. \left[ \dfrac{4r^3}{3} - \dfrac{r^5}{5} \right|_0^2 \right] \, d\theta = \int_0^{2\pi} \dfrac{64}{15} \,d\theta = \dfrac{128\pi}{15}\nonumber \]
Valor promedio de una función de tres variables
Recordemos que encontramos el valor promedio de una función de dos variables evaluando la doble integral sobre una región en el plano y luego dividiendo por el área de la región. De igual manera, podemos encontrar el valor promedio de una función en tres variables evaluando la triple integral sobre una región sólida y luego dividiendo por el volumen del sólido.
Si\(f(x,y,z)\) es integrable sobre una región delimitada sólida\(E\) con volumen positivo\(V \, (E),\), entonces el valor promedio de la función es
\[f_{ave} = \dfrac{1}{V \, (E)} \iiint_E f(x,y,z) \, dV. \nonumber \]
Tenga en cuenta que el volumen es
\[V \, (E) = \iiint_E 1 \,dV. \nonumber \]
La temperatura en un punto\((x,y,z)\) de un sólido\(E\) delimitado por los planos de coordenadas y el plano\(x + y + z = 1\) es\(T(x,y,z) = (xy + 8z + 20) \, \text{°}\text{C} \). Encuentra la temperatura promedio sobre el sólido.
Solución
Utilice el teorema dado anteriormente y la triple integral para encontrar el numerador y el denominador. Entonces haz la división. Observe que el avión\(x + y + z = 1\) tiene intercepciones\((1,0,0), \, (0,1,0),\) y\((0,0,1)\). La región\(E\) parece
\[E = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \, 0 \leq y \leq 1 - x, \, 0 \leq z \leq 1 - x - y \big\}.\nonumber \]
De ahí que la triple integral de la temperatura sea
\[\iiint_E f(x,y,z) \,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y} (xy + 8z + 20) \, dz \, dy \, dx = \dfrac{147}{40}. \nonumber \]
La evaluación del volumen es
\[V \, (E) = \iiint_E 1\,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y} 1 \,dz \, dy \, dx = \dfrac{1}{6}. \nonumber \]
De ahí que el valor promedio sea
\[ T_{ave} = \dfrac{147/40}{1/6} = \dfrac{6(147)}{40} = \dfrac{441}{20} \, \text{°}\text{C} \nonumber \].
Encuentra el valor promedio de la función\(f(x,y,z) = xyz\) sobre el cubo con lados de longitud 4 unidades en el primer octante con un vértice en el origen y bordes paralelos a los ejes de coordenadas.
- Pista
-
Sigue los pasos del ejemplo anterior.
- Contestar
-
\(f_{ave} = 8\)
Conceptos clave
- Para calcular una triple integral utilizamos el teorema de Fubini, que establece que si\(f(x,y,z)\) es continuo en una caja rectangular\(B = [a,b] \times [c,d] \times [e,f]\), entonces\[\iiint_B f(x,y,z) \,dV = \int_e^f \int_c^d \int_a^b f(x,y,z) \, dx \, dy \, dz \nonumber \] y también es igual a cualquiera de los otros cinco ordenamientos posibles para la triple integral iterada.
- Para calcular el volumen de una región delimitada sólida general\(E\) utilizamos la triple integral\[V \, (E) = \iiint_E 1 \,dV. \nonumber \]
- Intercambiar el orden de las integrales iteradas no cambia la respuesta. De hecho, intercambiar el orden de integración puede ayudar a simplificar el cálculo.
- Para calcular el valor promedio de una función sobre una región tridimensional general, utilizamos\[f_{ave} = \dfrac{1}{V \, (E)} \iiint_E f(x,y,z) \,dV. \nonumber \]
Ecuaciones Clave
- Triple integral
\[\lim_{l,m,n \rightarrow \infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(x_{ijk}^*, y_{ijk}^*, z_{ijk}^*) \,\Delta x \Delta y \Delta z = \iiint_B f(x,y,z) \,dV \nonumber \]
Glosario
- triple integral
- la triple integral de una función continua\(f(x,y,z)\) sobre una caja sólida rectangular\(B\) es el límite de una suma de Riemann para una función de tres variables, si este límite existe



Integrales triples sobre una región limitada general
Ahora ampliamos la definición de la triple integral para computar una triple integral sobre una región delimitada más general\(E\) en\(\mathbb{R}^3\). Las regiones delimitadas generales que consideraremos son de tres tipos. Primero, deja\(D\) ser la región delimitada que es una proyección de\(E\) sobre el\(xy\) plano. Supongamos que la región\(E\) en\(\mathbb{R}^3\) tiene la forma
\[E = \big\{(x,y,z)\,|\,(x,y) \in D, u_1(x,y) \leq z \leq u_2(x,y) \big\}. \nonumber \]
Para dos funciones\(z = u_1(x,y)\) y\(u_2(x,y)\), tal que\(u_1(x,y) \leq u_2(x,y)\) para todos\((x,y)\) en\(D\) como se muestra en la siguiente figura.