3.3: Reglas de diferenciación
- Page ID
- 116680
- Establezca las reglas constantes, múltiples constantes y de poder.
- Aplicar las reglas de suma y diferencia para combinar derivados.
- Utilice la regla del producto para encontrar la derivada de un producto de funciones.
- Utilice la regla del cociente para encontrar la derivada de un cociente de funciones.
- Extender la regla de potencia a funciones con exponentes negativos.
- Combinar las reglas de diferenciación para encontrar la derivada de una función polinómica o racional.
Encontrar derivadas de funciones usando la definición de la derivada puede ser un proceso largo y, para ciertas funciones, bastante desafiante. Por ejemplo, anteriormente encontramos que
\[\dfrac{d}{dx}\left(\sqrt{x}\right)=\dfrac{1}{2\sqrt{x}} \nonumber \]
mediante el uso de un proceso que implicaba multiplicar una expresión por un conjugado antes de evaluar un límite.
El proceso que podríamos utilizar para evaluar\(\dfrac{d}{dx}\left(\sqrt[3]{x}\right)\) usando la definición, aunque similar, es más complicado.
En esta sección, desarrollamos reglas para encontrar derivados que nos permitan eludir este proceso. Comenzamos con lo básico.
Las Reglas Básicas
Las funciones\(f(x)=c\) y\(g(x)=x^n\) donde\(n\) es un entero positivo son los bloques de construcción a partir de los cuales se construyen todos los polinomios y funciones racionales. Para encontrar derivados de polinomios y funciones racionales de manera eficiente sin recurrir a la definición límite de la derivada, primero debemos desarrollar fórmulas para diferenciar estas funciones básicas.
La Regla Constante
Primero aplicamos la definición límite de la derivada para encontrar la derivada de la función constante,\(f(x)=c\). Para esta función, ambos\(f(x)=c\) y\(f(x+h)=c\), así obtenemos el siguiente resultado:
\[\begin{align*} f′(x) &=\lim_{h→0} \dfrac{f(x+h)−f(x)}{h} \\[4pt] &=\lim_{h→0}\dfrac{c−c}{h} \\[4pt] &=\lim_{h→0}\dfrac{0}{h} \\[4pt] &=\lim_{h→0}0=0. \end{align*}\]
La regla para diferenciar funciones constantes se llama regla constante. Afirma que la derivada de una función constante es cero; es decir, dado que una función constante es una línea horizontal, la pendiente, o la tasa de cambio, de una función constante es\(0\). Reafirmamos esta regla en el siguiente teorema.
Que\(c\) sea una constante. Si\(f(x)=c\), entonces\(f′(x)=0.\)
Alternativamente, podemos expresar esta regla como
\[\dfrac{d}{dx}(c)=0. \nonumber \]
Encuentra la derivada de\(f(x)=8.\)
Solución
Esto es solo una aplicación de la regla en un solo paso:\(f′(8)=0.\)
Encuentra la derivada de\(g(x)=−3\).
- Pista
-
Usar el ejemplo anterior como guía
- Contestar
-
0
La regla del poder
Hemos demostrado que
\[\dfrac{d}{dx}\left(x^2\right)=2x\quad\text{ and }\quad\dfrac{d}{dx}\left(x^{1/2}\right)=\dfrac{1}{2}x^{−1/2}. \nonumber \]
En este punto, es posible que veas un patrón comenzando a desarrollarse para derivados de la forma\(\dfrac{d}{dx}\left(x^n\right)\). Continuamos nuestro examen de fórmulas derivadas diferenciando funciones de poder de la forma\(f(x)=x^n\) donde\(n\) es un entero positivo. Desarrollamos fórmulas para derivados de este tipo de función en etapas, comenzando con potencias enteras positivas. Antes de exponer y probar la regla general para derivadas de funciones de esta forma, echamos un vistazo a un caso específico,\(\dfrac{d}{dx}(x^3)\). A medida que avanzamos por esta derivación, prestar especial atención a la porción de la expresión en negrilla, ya que la técnica utilizada en este caso es esencialmente la misma que la técnica utilizada para probar el caso general.
Encuentra\(\dfrac{d}{dx}\left(x^3\right)\).
Solución:
| \(\displaystyle \dfrac{d}{dx}\left(x^3\right)=\lim_{h→0}\dfrac{(x+h)^3−x^3}{h}\) | |
| \(\displaystyle =\lim_{h→0}\dfrac{x^3+3x^2h+3xh^2+h^3−x^3}{h}\) | Observe que el primer término en la expansión de\((x+h)^3\) es\(x^3\) y el segundo término es\(3x^2h\). Todos los demás términos contienen poderes de\(h\) que son dos o mayores |
| \(\displaystyle =\lim_{h→0}\dfrac{3x^2h+3xh^2+h^3}{h}\) | En este paso se han cancelado\(x^3\) los términos, dejando sólo términos que contienen\(h\). |
| \(\displaystyle =\lim_{h→0}\dfrac{h(3x^2+3xh+h^2)}{h}\) | Facturar el factor común de\(h\). |
| \(\displaystyle =\lim_{h→0}(3x^2+3xh+h^2)\) | Después de cancelar el factor común de\(h\), el único término que no contiene\(h\) es\(3x^2\). |
| \(=3x^2\) | Déjalo\(h\) ir a\(0\). |
Encuentra\(\dfrac{d}{dx}\left(x^4\right).\)
- Pista
-
Utilice\((x+h)^4=x^4+4x^3h+6x^2h^2+4xh^3+h^4\) y siga el procedimiento descrito en el ejemplo anterior.
- Contestar
-
\(\dfrac{d}{dx}\left(x^4\right) = 4x^3\)
Como veremos, el procedimiento para encontrar la derivada de la forma general\(f(x)=x^n\) es muy similar. Aunque a menudo es imprudente sacar conclusiones generales a partir de ejemplos específicos, observamos que cuando diferenciamos\(f(x)=x^3\), el power on\(x\) se convierte en el coeficiente de\(x^2\) en la derivada y la potencia on\(x\) en la derivada disminuye en 1. El siguiente teorema establece que la regla de poder se mantiene para todos los poderes enteros positivos de\(x\). Eventualmente extenderemos este resultado a potencias enteras negativas. Posteriormente, veremos que esta regla también puede extenderse primero a los poderes racionales de\(x\) y luego a los poderes arbitrarios de\(x\). Tenga en cuenta, sin embargo, que esta regla no se aplica a las funciones en las que una constante se eleva a una potencia variable, como\(f(x)=3^x\).
Dejar\(n\) ser un entero positivo. Si\(f(x)=x^n\), entonces
\[f′(x)=nx^{n−1}. \nonumber \]
Alternativamente, podemos expresar esta regla como
\[\dfrac{d}{dx}\left(x^n\right)=nx^{n−1.} \nonumber \]
Para\(f(x)=x^n\) donde\(n\) es un entero positivo, tenemos
\[f′(x)=\lim_{h→0}\dfrac{(x+h)^n−x^n}{h}. \nonumber \]
Desde
\((x+h)^n=x^n+nx^{n−1}h+\binom{n}{2}x^{n−2}h^2+\binom{n}{3}x^{n−3}h^3+…+nxh^{n−1}+h^n,\)
vemos que
\((x+h)^n−x^n=nx^{n−1}h+\binom{n}{2}x^{n−2}h^2+\binom{n}{3}x^{n−3}h^3+…+nxh^{n−1}+h^n.\)
A continuación, divida ambos lados por h:
\(\dfrac{(x+h)^n−x^n}{h}=\dfrac{nx^{n−1}h+\binom{n}{2}x^{n−2}h^2+\binom{n}{3}x^{n−3}h^3+…+nxh^{n−1}+h^n}{h}.\)
Por lo tanto,
\(\dfrac{(x+h)^n−x^n}{h}=nx^{n−1}+\binom{n}{2}x^{n−2}h+\binom{n}{3}x^{n−3}h^2+…+nxh^{n−2}+h^{n−1}.\)
Por último,
\[f′(x)=\lim_{h→0}(nx^{n−1}+\binom{n}{2}x^{n−2}h+\binom{n}{3}x^{n−3}h^2+…+nxh^{n−2}+h^{n-1}) \nonumber \]
\(=nx^{n−1}.\)
□
Encuentra la derivada de la función\(f(x)=x^{10}\) aplicando la regla de poder.
Solución
Usando la regla de poder con\(n=10\), obtenemos
\[f'(x)=10x^{10−1}=10x^9. \nonumber \]
Encuentra la derivada de\(f(x)=x^7\).
- Pista
-
Usa la regla de poder con\(n=7.\)
- Contestar
-
\(f′(x)=7x^6\)
La suma, la diferencia y las reglas múltiples constantes
Encontramos nuestras próximas reglas de diferenciación analizando derivados de sumas, diferencias y múltiplos constantes de funciones. Así como cuando trabajamos con funciones, hay reglas que facilitan la búsqueda de derivadas de funciones que sumamos, restamos o multiplicamos por una constante. Estas reglas se resumen en el siguiente teorema.
Dejar\(f(x)\) y\(g(x)\) ser funciones diferenciables y\(k\) ser una constante. Entonces se mantiene cada una de las siguientes ecuaciones.
Regla de Suma. La derivada de la suma de una función\(f\) y una función\(g\) es la misma que la suma de la derivada de\(f\) y la derivada de\(g\).
\[\dfrac{d}{dx}\big(f(x)+g(x)\big)=\dfrac{d}{dx}\big(f(x)\big)+\dfrac{d}{dx}\big(g(x)\big); \nonumber \]
es decir,
\[\text{for }s(x)=f(x)+g(x),\quad s′(x)=f′(x)+g′(x). \nonumber \]
Regla de Diferencia. La derivada de la diferencia de una función\(f\) y una función\(g\) es la misma que la diferencia de la derivada de\(f\) y la derivada de\(g\):
\[\dfrac{d}{dx}(f(x)−g(x))=\dfrac{d}{dx}(f(x))−\dfrac{d}{dx}(g(x)); \nonumber \]
es decir,
\[\text{for }d(x)=f(x)−g(x),\quad d′(x)=f′(x)−g′(x). \nonumber \]
Regla Múltiple Constante. La derivada de una constante\(k\) multiplicada por una función\(f\) es la misma que la constante multiplicada por la derivada:
\[\dfrac{d}{dx}\big(kf(x)\big)=k\dfrac{d}{dx}\big(f(x)\big); \nonumber \]
es decir,
\[\text{for }m(x)=kf(x),\quad m′(x)=kf′(x). \nonumber \]
Aquí solo proporcionamos la prueba de la regla de la suma. El resto sigue de manera similar.
Para funciones diferenciables\(f(x)\) y\(g(x)\), establecemos\(s(x)=f(x)+g(x)\). Usando la definición límite de la derivada tenemos
\[s′(x)=\lim_{h→0}\dfrac{s(x+h)−s(x)}{h}.\nonumber \]
Al sustituir\(s(x+h)=f(x+h)+g(x+h)\) y\(s(x)=f(x)+g(x),\) obtenemos
\[s′(x)=\lim_{h→0}\dfrac{\big(f(x+h)+g(x+h)\big)−\big(f(x)+g(x)\big)}{h}.\nonumber \]
Reordenando y reagrupando los términos, tenemos
\[s′(x)=\lim_{h→0}\left(\dfrac{f(x+h)−f(x)}{h}+\dfrac{g(x+h)−g(x)}{h}\right).\nonumber \]
Ahora aplicamos la ley de suma para los límites y la definición del derivado para obtener
\[s′(x)=\lim_{h→0}\dfrac{f(x+h)−f(x)}{h}+\lim_{h→0}\dfrac{g(x+h)−g(x)}{h}=f′(x)+g′(x).\nonumber \]
□
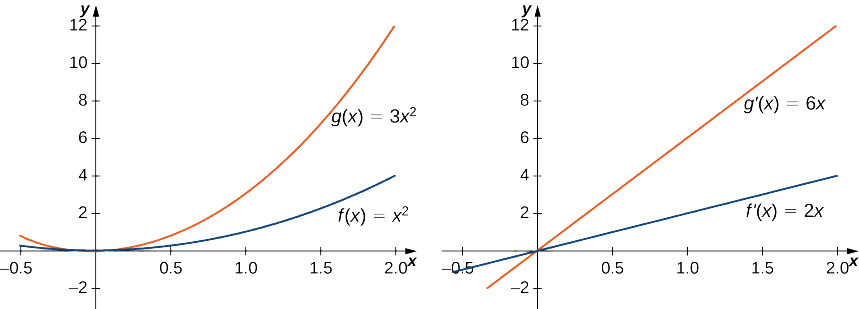
Encuentre la derivada de\(g(x)=3x^2\) y compárela con la derivada de\(f(x)=x^2.\)
Solución
Utilizamos la regla de poder directamente:
\[g′(x)=\dfrac{d}{dx}(3x^2)=3\dfrac{d}{dx}(x^2)=3(2x)=6x.\nonumber \]
Ya que\(f(x)=x^2\) tiene derivado\(f′(x)=2x\), vemos que la derivada de\(g(x)\) es 3 veces la derivada de\(f(x)\). Esta relación se ilustra en la Figura\(\PageIndex{1}\).
Encuentra la derivada de\(f(x)=2x^5+7\).
Solución
Comenzamos aplicando la regla para diferenciar la suma de dos funciones, seguida de las reglas para diferenciar múltiplos constantes de funciones y la regla para diferenciar poderes. Para comprender mejor la secuencia en la que se aplican las reglas de diferenciación, utilizamos la notación Leibniz a lo largo de la solución:
\ (\ begin {align*} f′ (x) &=\ dfrac {d} {dx}\ izquierda (2x^5+7\ derecha)\\ [4pt]
&=\ dfrac {d} {dx} (2x^5) +\ dfrac {d} {dx} (7) &\ text {Aplicar la regla de suma.}\\ [4pt]
&=2\ dfrac {d} {dx} (x^5) +\ dfrac {d} {dx} (7) &\ text {Aplicar la regla múltiple constante.}\\ [4pt]
&=2 (5 x^4) +0 & &\ text {Aplica la regla de potencia y la regla constante.}\\ [4pt]
&=10x^4 & &\ text {Simplificar.} \ end {alinear*}\)
Encuentra la derivada de\(f(x)=2x^3−6x^2+3.\)
- Pista
-
Utilice el ejemplo anterior como guía.
- Contestar
-
\(f′(x)=6x^2−12x.\)
Encuentra la ecuación de la línea tangente a la gráfica de\(f(x)=x^2−4x+6\) at\(x=1\)
Solución
Para encontrar la ecuación de la línea tangente, necesitamos un punto y una pendiente. Para encontrar el punto, compute
\[f(1)=1^2−4(1)+6=3. \nonumber \]
Esto nos da el punto\((1,3)\). Dado que la pendiente de la línea tangente en 1 es\(f′(1)\), primero debemos encontrar\(f′(x)\). Usando la definición de un derivado, tenemos
\[f′(x)=2x−4\nonumber \]
por lo que la pendiente de la línea tangente es\(f′(1)=−2\). Usando la fórmula punto-pendiente, vemos que la ecuación de la línea tangente es
\[y−3=−2(x−1).\nonumber \]
Poniendo la ecuación de la línea en forma pendiente-intercepción, obtenemos
\[y=−2x+5.\nonumber \]
Encuentra la ecuación de la línea tangente a la gráfica de\(f(x)=3x^2−11\) at\(x=2\). Utilice la forma punto-pendiente.
- Pista
-
Utilice el ejemplo anterior como guía.
- Contestar
-
\(y=12x−23\)
La regla del producto
Ahora que hemos examinado las reglas básicas, podemos comenzar a mirar algunas de las reglas más avanzadas. El primero examina la derivada del producto de dos funciones. Si bien puede ser tentador suponer que la derivada del producto es el producto de los derivados, similar a las reglas de suma y diferencia, la regla del producto no sigue este patrón. Para ver por qué no podemos usar este patrón, consideremos la función\(f(x)=x^2\), cuya derivada es\(f′(x)=2x\) y no\(\dfrac{d}{dx}(x)⋅\dfrac{d}{dx}(x)=1⋅1=1.\)
Dejar\(f(x)\) y\(g(x)\) ser funciones diferenciables. Entonces
\[\dfrac{d}{dx}(f(x)g(x))=\dfrac{d}{dx}(f(x))⋅g(x)+\dfrac{d}{dx}(g(x))⋅f(x). \nonumber \]
Es decir,
\[\text{if }p(x)=f(x)g(x),\quad \text{then }p′(x)=f′(x)g(x)+g′(x)f(x).\nonumber \]
Esto significa que la derivada de un producto de dos funciones es la derivada de la primera función multiplicada por la segunda función más la derivada de la segunda función por la primera función.
Comenzamos asumiendo que\(f(x)\) y\(g(x)\) son funciones diferenciables. En un punto clave de esta prueba necesitamos utilizar el hecho de que, como\(g(x)\) es diferenciable, también es continuo. En particular, utilizamos el hecho de que dado que\(g(x)\) es continuo,\(\displaystyle \lim_{h→0}g(x+h)=g(x).\)
Al aplicar la definición límite de la derivada para\(p(x)=f(x)g(x),\) obtener
\[ p′(x)=\lim_{h→0}\dfrac{f(x+h)g(x+h)−f(x)g(x)}{h}.\nonumber \]
Al sumar y restar\(f(x)g(x+h)\) en el numerador, tenemos
\[p′(x)=\lim_{h→0}\dfrac{f(x+h)g(x+h)−f(x)g(x+h)+f(x)g(x+h)−f(x)g(x)}{h}.\nonumber \]
Después de romper este cociente y aplicar la ley de suma para los límites, la derivada se convierte
\[p′(x)=\lim_{h→0}\dfrac{f(x+h)g(x+h)−f(x)g(x+h)}{h}+\lim_{h→0}\dfrac{f(x)g(x+h)−f(x)g(x)}{h}.\nonumber \]
Reordenando, obtenemos
\ [\ begin {align*} p′ (x) &=\ lim_ {h→0}\ izquierda (\ dfrac {f (x+h) −f (x)} {h} g (x+h)\ derecha) +\ lim_ {h→0}\ izquierda (\ dfrac {g (x+h) −g (x)} {h} f (x)\ derecha)\\ [4pt]
&=\ izquierda (\ lim_ {h→0}\ dfrac {f (x+h) −f (x)} {h}\ derecha) ⋅\ izquierda (\ lim_ {h→0}\; g (x+h)\ derecha) +\ izquierda (\ lim_ {h→0}\ dfrac {g (x+h) −g (x)} {h}\ derecha) f (x)\ final {alinear*}\]
Al utilizar la continuidad de\(g(x)\), la definición de los derivados de\(f(x)\) y\(g(x)\), y aplicando las leyes de límite, llegamos a la regla del producto,
\[p′(x)=f′(x)g(x)+g′(x)f(x).\nonumber \]
□
Para\(p(x)=f(x)g(x)\), use la regla del producto para encontrar\(p′(2)\) si\(f(2)=3,\; f′(2)=−4,\; g(2)=1\), y\(g′(2)=6\).
Solución
Desde\(p(x)=f(x)g(x)\),\(p′(x)=f′(x)g(x)+g′(x)f(x),\) y por lo tanto
\(p′(2)=f′(2)g(2)+g′(2)f(2)=(−4)(1)+(6)(3)=14.\)
Para\(p(x)=(x^2+2)(3x^3−5x),\) encontrar\(p′(x)\) aplicando la regla del producto. Verifique el resultado primero encontrando el producto y luego diferenciando.
Solución
Si nos fijamos\(f(x)=x^2+2\) y\(g(x)=3x^3−5x\), entonces\(f′(x)=2x\) y\(g′(x)=9x^2−5\). Por lo tanto,
\(p′(x)=f′(x)g(x)+g′(x)f(x)=(2x)(3x^3−5x)+(9x^2−5)(x^2+2).\)
Simplificando, tenemos
\[p′(x)=15x^4+3x^2−10. \nonumber \]
Para verificar, vemos eso\(p(x)=3x^5+x^3−10x\) y, en consecuencia,\(p′(x)=15x^4+3x^2−10.\)
Utilice la regla del producto para obtener la derivada de\(p(x)=2x^5(4x^2+x).\)
- Pista
-
Establecer\(f(x)=2x^5\)\(g(x)=4x^2+x\) y usar el ejemplo anterior como guía.
- Contestar
-
\(p′(x)=10x^4(4x^2+x)+(8x+1)(2x^5)=56x^6+12x^5.\)
La regla del cociente
Habiendo desarrollado y practicado la regla del producto, ahora consideramos diferenciar cocientes de funciones. Como vemos en el siguiente teorema, la derivada del cociente no es el cociente de las derivadas; más bien, es la derivada de la función en el numerador multiplicada por la función en el denominador menos la derivada de la función en el denominador multiplicada por la función en el numerador, todo dividido por el cuadrado de la función en el denominador. Para comprender mejor por qué no podemos simplemente tomar el cociente de los derivados, tenga en cuenta que
\[\dfrac{d}{dx}(x^2)=2x,\text{ not }\dfrac{\dfrac{d}{dx}(x^3)}{\dfrac{d}{dx}(x)}=\dfrac{3x^2}{1}=3x^2.\nonumber \]
Dejar\(f(x)\) y\(g(x)\) ser funciones diferenciables. Entonces
\[\dfrac{d}{dx}\left(\dfrac{f(x)}{g(x)}\right)=\dfrac{\dfrac{d}{dx}(f(x))⋅g(x)−\dfrac{d}{dx}(g(x))⋅f(x)}{\big(g(x)\big)^2}. \nonumber \]
Es decir, si
\[q(x)=\dfrac{f(x)}{g(x)}\nonumber \]
entonces
\[q′(x)=\dfrac{f′(x)g(x)−g′(x)f(x)}{\big(g(x)\big)^2}.\nonumber \]
La prueba de la regla del cociente es muy similar a la prueba de la regla del producto, por lo que aquí se omite. En cambio, aplicamos esta nueva regla para encontrar derivados en el siguiente ejemplo.
Usa la regla del cociente para encontrar la derivada de\(q(x)=\dfrac{5x^2}{4x+3}.\)
Solución
Dejar\(f(x)=5x^2\) y\(g(x)=4x+3\). Así,\(f′(x)=10x\) y\(g′(x)=4\).
Sustituyendo a la regla del cociente, tenemos
\[q′(x)=\dfrac{f′(x)g(x)−g′(x)f(x)}{(g(x))^2}=\dfrac{10x(4x+3)−4(5x^2)}{(4x+3)^2}.\nonumber \]
Simplificando, obtenemos
\[q′(x)=\dfrac{20x^2+30x}{(4x+3)^2}\nonumber \]
Encuentra la derivada de\(h(x)=\dfrac{3x+1}{4x−3}\).
- Pista
-
Aplicar la regla del cociente con\(f(x)=3x+1\) y\(g(x)=4x−3\).
- Contestar
-
\(h′(x)=−\dfrac{13}{(4x−3)^2}.\)
Ahora es posible usar la regla de cociente para extender la regla de poder para encontrar derivadas de funciones de la forma\(x^k\) donde\(k\) es un entero negativo.
Si\(k\) es un entero negativo, entonces
\[\dfrac{d}{dx}(x^k)=kx^{k−1}. \nonumber \]
Si\(k\) es un entero negativo, podemos establecer\(n=−k\), de modo que n es un entero positivo con\(k=−n\). Dado que para cada entero positivo\(n\)\(x^{−n}=\dfrac{1}{x^n}\),, ahora podemos aplicar la regla de cociente estableciendo\(f(x)=1\) y\(g(x)=x^n\). En este caso,\(f′(x)=0\) y\(g′(x)=nx^{n−1}\). Por lo tanto,
\[\dfrac{d}{dx}(x^{−n})=\dfrac{0(x^n)−1(nx^{n−1})}{(x^n)^2}.\nonumber \]
Simplificando, vemos que
\[\begin{align*} \dfrac{d}{dx}(x^{−n}) &=\dfrac{−nx^{n−1}}{x^{2n}}\\[4pt]&=−nx^{(n−1)−2n}\\[4pt]&=−nx^{−n−1}.\end{align*}\]
Por último, observar que ya que\(k=−n\), al sustituir tenemos
\[\dfrac{d}{dx}(x^k)=kx^{k−1}.\nonumber \]
□
Encuentra\(\dfrac{d}{dx}(x^{−4})\).
Solución
Al aplicar la regla de poder extendido con\(k=−4\), obtenemos
\[\dfrac{d}{dx}(x^{−4})=−4x^{−4−1}=−4x^{−5}.\nonumber \]
Utilice la regla de potencia extendida y la regla múltiple constante para encontrar\(f(x)=\dfrac{6}{x^2}\).
Solución
Puede parecer tentador usar la regla del cociente para encontrar esta derivada, y ciertamente no sería incorrecto hacerlo. Sin embargo, es mucho más fácil diferenciar esta función reescribiéndola primero como\(f(x)=6x^{−2}\).
\ (\ begin {align*} f′ (x) &=\ dfrac {d} {dx}\ izquierda (\ dfrac {6} {x^2}\ derecha) =\ dfrac {d} {dx}\ izquierda (6x^ {−2}\ derecha) &\ texto {Reescribir}\ dfrac {6} {x^2}\ texto {as} 6x^ {−2}.\\ [4pt]
&=6\ dfrac {d} {dx}\ left (x^ {−2}\ right) &\ text {Aplica la regla múltiple constante.}\\ [4pt]
&=6 (−2x^ { −3}) & &\ text {Usa la regla de potencia extendida para diferenciar} x^ {−2}.\\ [4pt]
&=−12x^ {−3} &\ text {Simplificar.} \ end {alinear*}\)
Encuentre la derivada del\(g(x)=\dfrac{1}{x^7}\) uso de la regla de potencia extendida.
- Pista
-
Reescribir\(g(x)=\dfrac{1}{x^7}=x^{−7}\). Utilice la regla de potencia extendida con\(k=−7\).
- Contestar
-
\(g′(x)=−7x^{−8}\).
Combinar reglas de diferenciación
Como hemos visto a lo largo de los ejemplos de esta sección, rara vez sucede que estamos llamados a aplicar una sola regla de diferenciación para encontrar la derivada de una función dada. En este punto, al combinar las reglas de diferenciación, podemos encontrar las derivadas de cualquier función polinómica o racional. Posteriormente encontraremos combinaciones más complejas de reglas de diferenciación. Una buena regla general para usar al aplicar varias reglas es aplicar las reglas a la inversa del orden en que evaluaríamos la función.
Para\(k(x)=3h(x)+x^2g(x)\), encontrar\(k′(x)\).
Solución: Encontrar esta derivada requiere la regla de suma, la regla múltiple constante y la regla del producto.
| \(k′(x)=\dfrac{d}{dx}\big(3h(x)+x^2g(x)\big)=\dfrac{d}{dx}\big(3h(x)\big)+\dfrac{d}{dx}\big(x^2g(x)\big)\) | Aplicar la regla de suma. |
| \(=3\dfrac{d}{dx}\big(h(x)\big)+\left(\dfrac{d}{dx}(x^2)g(x)+\dfrac{d}{dx}(g(x))x^2\right)\) | Aplicar la regla múltiple constante para diferenciar\(3h(x)\) y la regla del producto para diferenciar\(x^2g(x)\). |
| \(=3h′(x)+2xg(x)+g′(x)x^2\) |
Para\(k(x)=f(x)g(x)h(x)\), expreso\(k′(x)\) en términos de\(f(x),g(x),h(x)\), y sus derivados.
Solución
Podemos pensar en la función\(k(x)\) como el producto de la función\(f(x)g(x)\) y la función\(h(x)\). Es decir,\(k(x)=(f(x)g(x))⋅h(x)\). Por lo tanto,
\ (\ begin {align*} k′ (x) &=\ dfrac {d} {dx}\ grande (f (x) g (x)\ grande) h (x) +\ dfrac {d} {dx}\ grande (h (x)\ grande) ⋅\ grande (f (x) g (x)\ grande). & &\ text {Aplicar la regla del producto al producto de} f (x) g (x)\ text {y} h (x).\\ [4pt]
&=\ big (f′ (x) g (x) +g′ (x) f (x)\ big) h (x) +h′ (x) f (x) g (x) &\ text {Aplicar la regla del producto a} f (x) g (x)\\ [4pt]
&=f′ (x) g (x) h (x) +f (x) g′ (x) h (x) +f (x) g (x) h′ (x). & &\ text {Simplificar.} \ end {alinear*}\)
Para\(h(x)=\dfrac{2x^3k(x)}{3x+2}\), encontrar\(h′(x)\).
Solución
Este procedimiento es típico para encontrar la derivada de una función racional.
\ (\ begin {align*} h′ (x) &=\ dfrac {\ dfrac {d} {dx} (2x^3k (x)) ⋅ (3x+2) −\ dfrac {d} {dx} (3x+2) ⋅ (2x^3k (x))} {(3x+2) ^2} &\ text {Aplica la regla del cociente.}\ [4pt]
&=\ dfrac {(6x^2k (x) +k′ (x) 2x^3) (3x+2) −3 (2x^3k (x))} {(3x+2) ^2} &\ text {Aplica la regla del producto para encontrar}\ dfrac {d} {dx} (2x^3k (x)). \ text {Usar}\ dfrac {d} {dx} (3x+2) =3.\\ [4pt]
&=\ dfrac {−6x^3k (x) +18x^3k (x) +12x^2k (x) +6x^4k′ (x) +4x^3k′ (x)} {(3x+2) ^2} &\ texto {Simplificar}\ end {alinear*}\)
Encuentra\(\dfrac{d}{dx}(3f(x)−2g(x)).\)
- Pista
-
Aplicar la regla de diferencia y la regla múltiple constante.
- Contestar
-
\(3f′(x)−2g′(x).\)
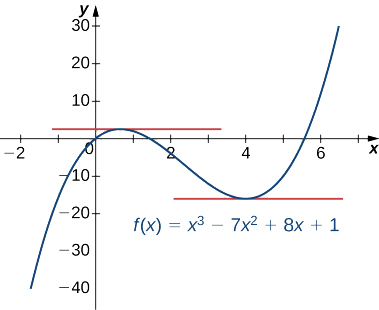
Determinar los valores de\(x\) para los cuales\(f(x)=x^3−7x^2+8x+1\) tiene una línea tangente horizontal.
Solución
Para encontrar los valores de\(x\) para los cuales\(f(x)\) tiene una línea tangente horizontal, debemos resolver\(f′(x)=0\).
Dado que\(f′(x)=3x^2−14x+8=(3x−2)(x−4)\),
debemos resolver\((3x−2)(x−4)=0\). Así vemos que la función tiene líneas tangentes horizontales en\(x=\dfrac{2}{3}\) y\(x=4\) como se muestra en la siguiente gráfica.
La posición de un objeto en un eje de coordenadas en el tiempo\(t\) viene dada por\(s(t)=\dfrac{t}{t^2+1}.\) ¿Cuál es la velocidad inicial del objeto?
Solución
Dado que la velocidad inicial se\(v(0)=s′(0),\) inicia\(s′(t)\) por encontrar aplicando la regla del cociente:
\(s′(t)=\dfrac{1(t^2+1)−2t(t)}{(t^2+1)^2}=\dfrac{1−t^2}{(t^2+1)^2}\).
Después de evaluar, vemos que\(v(0)=1.\)
Encuentra los valores de\(x\) para los cuales la línea tangente a la gráfica de\(f(x)=4x^2−3x+2\) tiene una línea tangente paralela a la línea\(y=2x+3.\)
- Pista
-
Resolver\(f′(x)=2\).
- Contestar
-
\(\dfrac{5}{8}\)
Las carreras de autos de Fórmula Uno pueden ser muy emocionantes de ver y atraer a muchos espectadores. Los diseñadores de pistas de Fórmula Uno deben garantizar que haya suficiente espacio disponible en la tribuna alrededor de la pista para acomodar a estos espectadores. Sin embargo, las carreras de autos pueden ser peligrosas y las consideraciones de seguridad son primordiales. Las tribunas deben colocarse donde los espectadores no estarán en peligro en caso de que un conductor pierda el control de un automóvil (Figura\(\PageIndex{3}\)).
La seguridad es especialmente una preocupación en los giros. Si un conductor no disminuye la velocidad suficiente antes de ingresar al giro, el automóvil puede deslizarse fuera de la pista de carreras. Normalmente, esto solo da como resultado un giro más amplio, lo que ralentiza al conductor. Pero si el conductor pierde el control por completo, el auto puede volar fuera de la pista por completo, en un camino tangente a la curva del hipódromo.
Supongamos que está diseñando una nueva pista de Fórmula Uno. Una sección de la pista puede ser modelada por la función\(f(x)=x^3+3x^2+x\) (Figura\(\PageIndex{4}\)). El plan actual exige que se construyan tribunas a lo largo de la primera recta y alrededor de una porción de la primera curva. Los planos exigen que la esquina delantera de la tribuna se ubique en el punto (\(−1.9,2.8\)). Queremos determinar si esta ubicación pone en peligro a los espectadores si un conductor pierde el control del automóvil.
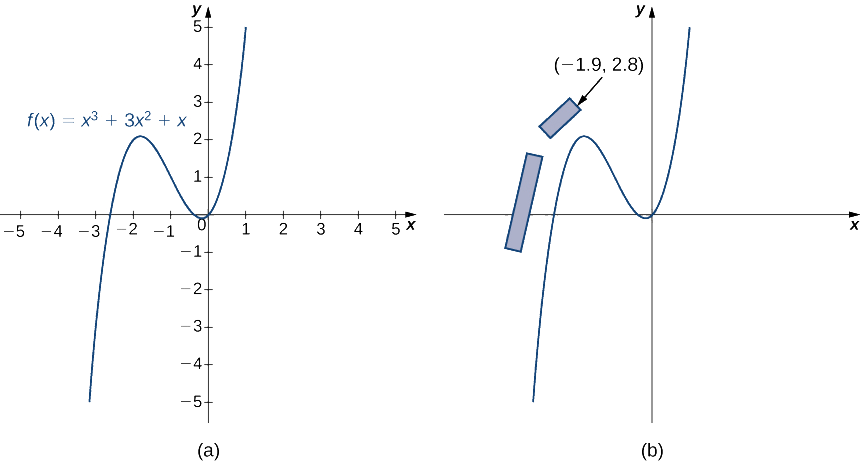
- Los físicos han determinado que es más probable que los conductores pierdan el control de sus autos ya que van entrando en un giro, en el punto donde la pendiente de la línea tangente es 1. Encuentra las\((x,y)\) coordenadas de este punto cerca del giro.
- Encuentra la ecuación de la línea tangente a la curva en este punto.
- Para determinar si los espectadores están en peligro en este escenario, encuentra la\(x\) coordenada del punto donde la línea tangente cruza la línea\(y=2.8\). ¿Este punto está seguro a la derecha de la tribuna? ¿O los espectadores están en peligro?
- ¿Y si un conductor pierde el control antes de lo que proyectan los físicos? Supongamos que un conductor pierde el control en el punto (\(−2.5,0.625\)). ¿Cuál es la pendiente de la línea tangente en este punto?
- Si un conductor pierde el control como se describe en la parte 4, ¿están seguros los espectadores?
- ¿Debe continuar con el diseño actual para la tribuna, o deben trasladarse las tribunas?
Conceptos clave
- La derivada de una función constante es cero.
- La derivada de una función de potencia es una función en la que el encendido\(x\) se convierte en el coeficiente del término y el poder encendido\(x\) en la derivada disminuye en 1.
- La derivada de una constante\(c\) multiplicada por una función\(f\) es la misma que la constante multiplicada por la derivada.
- La derivada de la suma de una función\(f\) y una función\(g\) es la misma que la suma de la derivada de\(f\) y la derivada de\(g\).
- La derivada de la diferencia de una función\(f\) y una función\(g\) es la misma que la diferencia de la derivada de\(f\) y la derivada de\(g\).
- La derivada de un producto de dos funciones es la derivada de la primera función multiplicada por la segunda función más la derivada de la segunda función por la primera función.
- La derivada del cociente de dos funciones es la derivada de la primera función multiplicada por la segunda función menos la derivada de la segunda función por la primera función, todas divididas por el cuadrado de la segunda función.
- Se utilizó la definición límite de la derivada para desarrollar fórmulas que nos permitan encontrar derivados sin recurrir a la definición de la derivada. Estas fórmulas se pueden utilizar individualmente o en combinación entre sí.
Glosario
- regla múltiple constante
- la derivada de una constante\(c\) multiplicada por una función\(f\) es la misma que la constante multiplicada por la derivada:\(\dfrac{d}{dx}\big(cf(x)\big)=cf′(x)\)
- regla constante
- la derivada de una función constante es cero:\(\dfrac{d}{dx}(c)=0\), donde\(c\) es una constante
- regla de diferencia
- la derivada de la diferencia de una función\(f\) y una función\(g\) es la misma que la diferencia de la derivada de\(f\) y la derivada de\(g\):\(\dfrac{d}{dx}\big(f(x)−g(x)\big)=f′(x)−g′(x)\)
- regla de poder
- la derivada de una función power es una función en la que el power on\(x\) se convierte en el coeficiente del término y el power on\(x\) en la derivada disminuye en 1: Si\(n\) es un entero, entonces\(\dfrac{d}{dx}\left(x^n\right)=nx^{n−1}\)
- regla del producto
- la derivada de un producto de dos funciones es la derivada de la primera función multiplicada por la segunda función más la derivada de la segunda función por la primera función:\(\dfrac{d}{dx}\big(f(x)g(x)\big)=f′(x)g(x)+g′(x)f(x)\)
- regla del cociente
- la derivada del cociente de dos funciones es la derivada de la primera función multiplicada por la segunda función menos la derivada de la segunda función por la primera función, todas divididas por el cuadrado de la segunda función:\(\dfrac{d}{dx}\left(\dfrac{f(x)}{g(x)}\right)=\dfrac{f′(x)g(x)−g′(x)f(x)}{\big(g(x)\big)^2}\)
- regla de suma
- la derivada de la suma de una función\(f\) y una función\(g\) es la misma que la suma de la derivada de\(f\) y la derivada de\(g\):\(\dfrac{d}{dx}\big(f(x)+g(x)\big)=f′(x)+g′(x)\)