4.8: Regla de L'Hôpital
- Page ID
- 116475
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Reconocer cuándo aplicar la regla de L'Hôpital.
- Identificar formas indeterminadas producidas por cocientes, productos, restaciones y poderes, y aplicar la regla de L'Hôpital en cada caso.
- Describir las tasas de crecimiento relativo de las funciones.
En esta sección, examinamos una poderosa herramienta para evaluar límites. Esta herramienta, conocida como regla de L'Hôpital, utiliza derivados para calcular límites. Con esta regla, podremos evaluar muchos límites que aún no hemos podido determinar. En lugar de apoyarnos en la evidencia numérica para conjeturar que existe un límite, podremos demostrar definitivamente que existe un límite y determinar su valor exacto.
Aplicando la Regla de L'Hôpital
La regla de L'Hôpital se puede utilizar para evaluar límites que involucran el cociente de dos funciones. Considerar
\[\lim_{x→a}\dfrac{f(x)}{g(x)}. \nonumber \]
Si\(\displaystyle \lim_{x→a}f(x)=L_1\) y\(\displaystyle \lim_{x→a}g(x)=L_2≠0,\) entonces
\[\lim_{x→a}\dfrac{f(x)}{g(x)}=\dfrac{L_1}{L_2}. \nonumber \]
Sin embargo, ¿qué pasa si\(\displaystyle \lim_{x→a}f(x)=0\) y\(\displaystyle \lim_{x→a}g(x)=0\)? A ésta la llamamos una de las formas indeterminadas, de tipo\(\dfrac{0}{0}\). Esto se considera una forma indeterminada porque no podemos determinar el comportamiento exacto de\(\dfrac{f(x)}{g(x)}\) as\(x→a\) sin más análisis. Hemos visto ejemplos de esto anteriormente en el texto. Por ejemplo, considere
\[\lim_{x→2}\dfrac{x^2−4}{x−2} \nonumber \]
y
\[\lim_{x→0}\dfrac{\sin x}{x}.\nonumber \]
Para el primero de estos ejemplos, podemos evaluar el límite factorizando el numerador y escribiendo
\[\lim_{x→2}\dfrac{x^2−4}{x−2}=\lim_{x→2}\dfrac{(x+2)(x−2)}{x−2}=\lim_{x→2}(x+2)=2+2=4. \nonumber \]
Porque\(\displaystyle \lim_{x→0}\dfrac{\sin x}{x}\) pudimos mostrar, usando un argumento geométrico, que
\[\lim_{x→0}\dfrac{\sin x}{x}=1. \nonumber \]
Aquí utilizamos una técnica diferente para evaluar límites como estos. Esta técnica no sólo proporciona una manera más fácil de evaluar estos límites, sino que además, y lo que es más importante, nos proporciona una manera de evaluar muchos otros límites que no podíamos calcular previamente.
La idea detrás de la regla de L'Hôpital puede explicarse mediante aproximaciones lineales locales. Consideremos dos funciones diferenciables\(f\) y\(g\) tal que\(\displaystyle \lim_{x→a}f(x)=0=\lim_{x→a}g(x)\) y tal que\(g′(a)≠0\) Para\(x\) cerca\(a\), podemos escribir
\[f(x)≈f(a)+f′(a)(x−a) \nonumber \]
y
\[g(x)≈g(a)+g′(a)(x−a). \nonumber \]
Por lo tanto,
\[\dfrac{f(x)}{g(x)}≈\dfrac{f(a)+f′(a)(x−a)}{g(a)+g′(a)(x−a)}. \nonumber \]
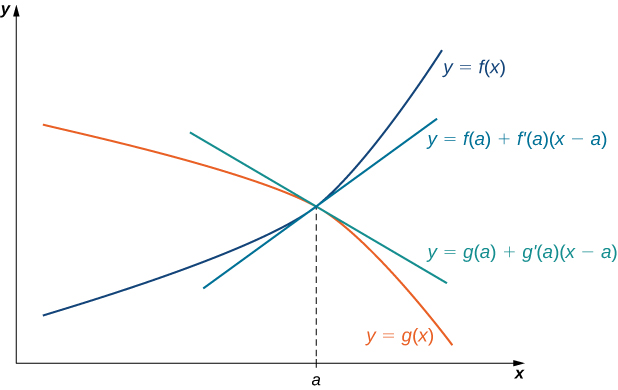
Ya que\(f\) es diferenciable en\(a\), entonces\(f\) es continuo en\(a\), y por lo tanto\(\displaystyle f(a)=\lim_{x→a}f(x)=0\). De igual manera,\(\displaystyle g(a)=\lim_{x→a}g(x)=0\). Si también asumimos eso\(f′\) y\(g′\) somos continuos en\(x=a\), entonces\(\displaystyle f′(a)=\lim_{x→a}f′(x)\) y\(\displaystyle g′(a)=\lim_{x→a}g′(x)\). Usando estas ideas, concluimos que
\[\lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)(x−a)}{g′(x)(x−a)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)} . \nonumber \]
Tenga en cuenta que la suposición de que\(f′\) y\(g′\) son continuos en\(a\) y se\(g′(a)≠0\) pueden aflojar. Expresamos formalmente la regla de L'Hôpital para la forma indeterminada\(\dfrac{0}{0}\). También tenga en cuenta que la notación\(\dfrac{0}{0}\) no significa que en realidad estemos dividiendo cero por cero. Más bien, estamos usando la notación\(\dfrac{0}{0}\) para representar un cociente de límites, cada uno de los cuales es cero.
Supongamos\(f\) y\(g\) son funciones diferenciables sobre un intervalo abierto que contiene\(a\), excepto posiblemente en\(a\). Si\(\displaystyle \lim_{x→a}f(x)=0\) y\(\displaystyle \lim_{x→a}g(x)=0,\) entonces
\[\lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)}, \nonumber \]
asumiendo que el límite al derecho existe o es\(∞\) o\(−∞\). Este resultado también se mantiene si estamos considerando límites unilaterales,\(a=∞\) o si\(a=−∞.\)
Proporcionamos una prueba de este teorema en el caso especial cuando\(f,g,f′,\) y\(g′\) son todos continuos a lo largo de un intervalo abierto que contiene\(a\). En ese caso, desde\(\displaystyle\lim_{x→a}f(x)=0=\lim_{x→a}g(x)\) y\(f\) y\(g\) son continuos en\(a\), se deduce que\(f(a)=0=g(a)\). Por lo tanto,
\ [\ begin {alinear*}\ lim_ {x→a}\ dfrac {f (x)} {g (x)} &=\ lim_ {x→a}\ dfrac {f (x) −f (a)} {g (x) −g (a)} &\ text {Desde}\, f (a) =0=g (a)\\ [4pt]
&=\ lim_ {x→a}\ dfrac {\ dfrac {f (x) −f (a)} {x−a}} {\ dfrac {g (x) −g (a)} {x−a}} &\ text {Multiplica numerador y denominador por}\,\ frac {1} {x-a}\\ [4pt]
&=\ frac {\ displaystyle\ lim_ {x→a}\ dfrac {f (x) −f (a)} {x−a}} {\ displaystyle\ lim_ {x→a}\ dfrac {g (x) −g (a)} {x−a}} &\ text {El límite de un cociente es el cociente de los límites.}\\ [4pt]
&=\ dfrac {f′ (a)} {g′ (a)} & &\ text {Por la definición de la derivada}\\ [4pt]
&=\ frac {\ displaystyle\ lim_ {x→a} f′ (x)} {\ displaystyle\ lim_ {x→a} g′ (x)} & &\ text {Por la continuidad de}\, f′\,\ text {y}\, g′\\ [4pt]
&=\ lim_ {x→a}\ dfrac {f′ (x)} g′ (x)}. & &\ text {El límite de un cociente}\ end {align*}\]
Tenga en cuenta que la regla de L'Hôpital establece que podemos calcular el límite de un cociente\(\dfrac{f}{g}\) considerando el límite del cociente de los derivados\(\dfrac{f′}{g′}\). Es importante darse cuenta de que no estamos calculando la derivada del cociente\(\dfrac{f}{g}\).
□
Evaluar cada uno de los siguientes límites aplicando la regla de L'Hôpital.
- \(\displaystyle \lim_{x→0}\dfrac{1−\cos x}{x}\)
- \(\displaystyle \lim_{x→1}\dfrac{\sin(πx)}{\ln x}\)
- \(\displaystyle \lim_{x→∞}\dfrac{e^{1/x}−1}{1/x}\)
- \(\displaystyle \lim_{x→0}\dfrac{\sin x−x}{x^2}\)
Solución
a. desde el numerador\(1−\cos x→0\) y el denominador\(x→0\), podemos aplicar la regla de L'Hôpital para evaluar este límite. Tenemos
\[\lim_{x→0}\dfrac{1−\cos x}{x}=\lim_{x→0}\dfrac{\dfrac{d}{dx}\big(1−\cos x\big)}{\dfrac{d}{dx}\big(x\big)}=\lim_{x→0}\dfrac{\sin x}{1}=\frac{\displaystyle \lim_{x→0}\sin x}{\displaystyle \lim_{x→0}1}=\dfrac{0}{1}=0. \nonumber \]
b. como\(x→1,\) numerador\(\sin(πx)→0\) y denominador\(\ln(x)→0.\) Por lo tanto, podemos aplicar la regla de L'Hôpital. Obtenemos
\[\begin{align*} \lim_{x→1}\dfrac{\sin(πx)}{\ln x}&=\lim_{x→1}\dfrac{π \cos(πx)}{1/x} \\[4pt] &=\lim_{x→1}(πx)\cos(πx) \\[4pt] &=(π⋅1)(−1)=−π. \end{align*} \nonumber \]
c. As\(x→∞\), el numerador\(e^{1/x}−1→0\) y el denominador\(\frac{1}{x}→0\). Por lo tanto, podemos aplicar la regla de L'Hôpital. Obtenemos
\[\lim_{x→∞}\dfrac{e^{1/x}−1}{\dfrac{1}{x}}=\lim_{x→∞}\dfrac{e^{1/x}(\tfrac{−1}{x^2})}{\left(\frac{−1}{x^2}\right)}=\lim_{x→∞}e^{1/x}=e^0=1. \nonumber \]
d. A medida que\(x→0,\) tanto el numerador como el denominador se acercan a cero. Por lo tanto, podemos aplicar la regla de L'Hôpital. Obtenemos
\[\lim_{x→0}\dfrac{\sin x−x}{x^2}=\lim_{x→0}\dfrac{\cos x−1}{2x}.\nonumber \]
Dado que el numerador y denominador de este nuevo cociente ambos se acercan a cero como\(x→0\), aplicamos nuevamente la regla de L'Hôpital. Al hacerlo, vemos que
\[\lim_{x→0}\dfrac{\cos x−1}{2x}=\lim_{x→0}\dfrac{−\sin x}{2}=0. \nonumber \]
Por lo tanto, concluimos que
\[\lim_{x→0}\dfrac{\sin x−x}{x^2}=0. \nonumber \]
Evaluar\[\lim_{x→0}\dfrac{x}{\tan x}. \nonumber \]
- Pista
-
\(\dfrac{d}{dx}\big(\tan x\big)=\sec^2x\)
- Responder
-
\(1\)
También podemos utilizar la regla de L'Hôpital para evaluar límites de cocientes\(\dfrac{f(x)}{g(x)}\) en los que\(f(x)→±∞\) y\(g(x)→±∞\). Los límites de esta forma se clasifican como formas indeterminadas de tipo\(∞/∞\). Nuevamente, tenga en cuenta que en realidad no estamos dividiendo\(∞\) por\(∞\). Ya que no\(∞\) es un número real, eso es imposible; más bien,\(∞/∞\) se utiliza para representar un cociente de límites, cada uno de los cuales es\(∞\) o\(−∞\).
Supongamos\(f\) y\(g\) son funciones diferenciables sobre un intervalo abierto que contiene\(a\), excepto posiblemente en\(a\). Supongamos\(\displaystyle\lim_{x→a}f(x)=∞\) (o\(−∞\)) y\(\displaystyle\lim_{x→a}g(x)=∞\) (o\(−∞\)). Entonces,
\[\lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)} \nonumber \]
asumiendo que el límite al derecho existe o es\(∞\) o\(−∞\). Este resultado también se mantiene si el límite es infinito, si\(a=∞\) o\(−∞\), o el límite es unilateral.
Evaluar cada uno de los siguientes límites aplicando la regla de L'Hôpital.
- \(\displaystyle\lim_{x→\infty}\dfrac{3x+5}{2x+1}\)
- \(\displaystyle \lim_{x→0^+}\dfrac{\ln x}{\cot x}\)
Solución
a. desde\(3x+5\) and \(2x+1\) are first-degree polynomials with positive leading coefficients, \(\displaystyle\lim_{x→∞}(3x+5)=∞\) and \(\displaystyle\lim_{x→∞}(2x+1)=∞\). Therefore, we apply L’Hôpital’s rule and obtain
\[\lim_{x→∞}\dfrac{3x+5}{2x+1}=\lim_{x→∞}\dfrac{3}{2}=\dfrac{3}{2}.\nonumber \]
Tenga en cuenta que este límite también se puede calcular sin invocar la regla de L'Hôpital. Anteriormente en el capítulo mostramos cómo evaluar tal límite dividiendo el numerador y el denominador por la mayor potencia de x en el denominador. Al hacerlo, vimos que
\[\lim_{x→∞}\dfrac{3x+5}{2x+1}=\lim_{x→∞}\dfrac{3+5/x}{2+1/x}=\dfrac{3}{2}. \nonumber \]
La regla de L'Hôpital nos proporciona un medio alternativo para evaluar este tipo de límites.
b. Aquí,\(\displaystyle \lim_{x→0^+}\ln x=−∞\) y\(\displaystyle \lim_{x→0^+}\cot x=∞\). Por lo tanto, podemos aplicar la regla de L'Hôpital y obtener
\[\lim_{x→0^+}\dfrac{\ln x}{\cot x}=\lim_{x→0^+}\dfrac{1/x}{−\csc^2x}=\lim_{x→0^+}\dfrac{1}{−x \csc^2x}. \nonumber \]
Ahora como\(x→0^+, \csc^2x→∞\). Therefore, the first term in the denominator is approaching zero and the second term is getting really large. In such a case, anything can happen with the product. Therefore, we cannot make any conclusion yet. To evaluate the limit, we use the definition of \(\csc x\) to write
\[\lim_{x→0^+}\dfrac{1}{−x \csc^2x}=\lim_{x→0^+}\dfrac{\sin^2x}{−x}. \nonumber \]
Ahora\(\displaystyle\lim_{x→0^+}\sin^2x=0\) and \(\displaystyle\lim_{x→0^+}-x=0\), so we apply L’Hôpital’s rule again. We find
\[\lim_{x→0^+}\dfrac{\sin^2x}{−x}=\lim_{x→0^+}\dfrac{2\sin x\cos x}{−1}=\dfrac{0}{−1}=0. \nonumber \]
Concluimos que
\[\lim_{x→0^+}\dfrac{\ln x}{\cot x}=0. \nonumber \]
Evaluar\[\lim_{x→∞}\dfrac{\ln x}{5x}. \nonumber \]
- Pista
-
\(\dfrac{d}{dx}\big(\ln x\big)=\dfrac{1}{x}\)
- Responder
-
\(0\)
Como se mencionó, la regla de L'Hôpital es una herramienta extremadamente útil para evaluar límites. Es importante recordar, sin embargo, que para aplicar la regla de L'Hôpital a un cociente\(\dfrac{f(x)}{g(x)}\), it is essential that the limit of \(\dfrac{f(x)}{g(x)}\) be of the form \(\dfrac{0}{0}\) or \(∞/∞\). Consider the following example.
Considerar\(\displaystyle\lim_{x→1}\dfrac{x^2+5}{3x+4}.\)
Demostrar que el límite no puede ser evaluado aplicando la regla de L'Hôpital.
Solución
Debido a que los límites del numerador y denominador no son ambos cero y no son ambos infinitos, no podemos aplicar la regla de L'Hôpital. Si tratamos de hacerlo, obtenemos
\[\dfrac{d}{dx}(x^2+5)=2x\nonumber \]
y
\[\dfrac{d}{dx}(3x+4)=3. \nonumber \]
En ese momento concluiríamos erróneamente que
\[\lim_{x→1}\dfrac{x^2+5}{3x+4}=\lim_{x→1}\dfrac{2x}{3}=\dfrac{2}{3}. \nonumber \]
Sin embargo, desde\(\displaystyle \lim_{x→1}(x^2+5)=6\) y en realidad\(\displaystyle \lim_{x→1}(3x+4)=7,\) tenemos
\[\lim_{x→1}\dfrac{x^2+5}{3x+4}=\dfrac{6}{7}. \nonumber \]
Podemos concluir que
\[\lim_{x→1}\dfrac{x^2+5}{3x+4}≠\lim_{x→1}\dfrac{\dfrac{d}{dx}(x^2+5)}{\dfrac{d}{dx}(3x+4).} \nonumber \]
Explique por qué no podemos aplicar la regla de L'Hôpital para evaluar\(\displaystyle\lim_{x→0^+}\dfrac{\cos x}{x}\). Evaluar\(\displaystyle\lim_{x→0^+}\dfrac{\cos x}{x}\) por otros medios.
- Pista
-
Determinar los límites del numerador y denominador por separado.
- Responder
-
\(\displaystyle\lim_{x→0^+}\cos x=1.\)Por lo tanto, no podemos aplicar la regla de L'Hôpital. El límite del cociente es\(∞.\)
Otras formas indeterminadas
La regla de L'Hôpital es muy útil para evaluar límites que involucran las formas indeterminadas\(\dfrac{0}{0}\) y\(∞/∞\). Sin embargo, también podemos usar la regla de L'Hôpital para ayudar a evaluar límites que involucran otras formas indeterminadas que surgen al evaluar límites. Las expresiones\(0⋅∞, ∞−∞, 1^∞, ∞^0\), y\(0^0\) son todas consideradas formas indeterminadas. Estas expresiones no son números reales. Más bien, representan formas que surgen al tratar de evaluar ciertos límites. A continuación nos damos cuenta de por qué se trata de formas indeterminadas y luego entendemos cómo utilizar la regla de L'Hôpital en estos casos. La idea clave es que debemos reescribir las formas indeterminadas de tal manera que lleguemos a la forma indeterminada\(\dfrac{0}{0}\) o\(∞/∞\).
Forma indeterminada de tipo 0∞
Supongamos que queremos evaluar\(\displaystyle \lim_{x→a}(f(x)⋅g(x))\), dónde\(f(x)→0\) y\(g(x)→∞\) (o\(−∞\)) como\(x→a\). Dado que un término en el producto se acerca a cero pero el otro término se está volviendo arbitrariamente grande (en magnitud), cualquier cosa le puede pasar al producto. Utilizamos la notación\(0⋅∞\) para denotar la forma que surge en esta situación. La expresión\(0⋅∞\) se considera indeterminada porque no podemos determinar sin más análisis el comportamiento exacto del producto\(f(x)g(x)\) como\(x→∞\). Por ejemplo, vamos a\(n\) ser un entero positivo y considerar
\(f(x)=\dfrac{1}{(x^n+1)}\)y\(g(x)=3x^2\).
Como\(x→∞, f(x)→0\) y\(g(x)→∞\). Sin embargo, el límite a partir\(x→∞\) de\(f(x)g(x)=\dfrac{3x^2}{(x^n+1)}\) varía, dependiendo de\(n\). Si\(n=2\), entonces\(\displaystyle\lim_{x→∞}f(x)g(x)=3\). Si\(n=1\), entonces\(\displaystyle\lim_{x→∞}f(x)g(x)=∞\). Si\(n=3\), entonces\(\displaystyle\lim_{x→∞}f(x)g(x)=0\). Aquí consideramos otro límite que involucra la forma indeterminada\(0⋅∞\) y mostramos cómo reescribir la función como cociente para usar la regla de L'Hôpital.
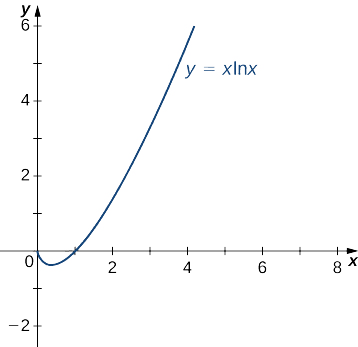
Evaluar\(\displaystyle \lim_{x→0^+}x\ln x.\)
Solución
Primero, reescribir la función\(x\ln x\) como cociente para aplicar la regla de L'Hôpital. Si escribimos
\[x\ln x=\dfrac{\ln x}{1/x} \nonumber \]
vemos eso\(\ln x→−∞\) como\(x→0^+\) y\(\dfrac{1}{x}→∞\) como\(x→0^+\). Por lo tanto, podemos aplicar la regla de L'Hôpital y obtener
\[\lim_{x→0^+}\dfrac{\ln x}{1/x}=\lim_{x→0^+}\dfrac{\dfrac{d}{dx}\big(\ln x\big)}{\dfrac{d}{dx}\big(1/x\big)}=\lim_{x→0^+}\dfrac{1/x}{−1/x^2}=\lim_{x→0^+}(−x)=0. \nonumber \]
Concluimos que
\[\lim_{x→0^+}x\ln x=0. \nonumber \]
Evaluar\[\lim_{x→0}x\cot x. \nonumber \]
- Pista
-
Escribir\(x\cot x=\dfrac{x \cos x}{\sin x}\)
- Responder
-
\(1\)
Forma indeterminada de tipo\(∞−∞\)
Otro tipo de forma indeterminada es\(∞−∞.\) Considera el siguiente ejemplo. Dejar\(n\) ser un entero positivo y let\(f(x)=3x^n\) y\(g(x)=3x^2+5\). Como\(x→∞, f(x)→∞\) y\(g(x)→∞\). Nos interesa\(\displaystyle\lim_{x→∞}(f(x)−g(x))\). Dependiendo de si\(f(x)\) crece más rápido,\(g(x)\) crece más rápido, o crecen al mismo ritmo, como vemos a continuación, cualquier cosa puede pasar en este límite. Desde\(f(x)→∞\) y\(g(x)→∞\), escribimos\(∞−∞\) para denotar la forma de este límite. Al igual que con nuestras otras formas indeterminadas, no\(∞−∞\) tiene sentido por sí solo y debemos hacer más análisis para determinar el valor del límite. Por ejemplo, supongamos que el exponente n en la función\(f(x)=3x^n\) es\(n=3\), entonces
\[\lim_{x→∞}(f(x)−g(x))=\lim_{x→∞}(3x^3−3x^2−5)=∞. \nonumber \]
Por otro lado, si\(n=2,\) entonces
\[\lim_{x→∞}(f(x)−g(x))=\lim_{x→∞}(3x^2−3x^2−5)=−5. \nonumber \]
Sin embargo, si\(n=1\), entonces
\[\lim_{x→∞}(f(x)−g(x))=\lim_{x→∞}(3x−3x^2−5)=−∞. \nonumber \]
Por lo tanto, el límite no puede determinarse considerando únicamente\(∞−∞\). A continuación vemos cómo reescribir una expresión que involucra la forma indeterminada\(∞−∞\) como fracción para aplicar la regla de L'Hôpital.
Evaluar\[\lim_{x→0^+}\left(\dfrac{1}{x^2}−\dfrac{1}{\tan x}\right). \nonumber \]
Solución
Al combinar las fracciones, podemos escribir la función como un cociente. Como el mínimo denominador común es\(x^2\tan x,\) que tenemos
\(\dfrac{1}{x^2}−\dfrac{1}{\tan x}=\dfrac{(\tan x)−x^2}{x^2\tan x}\).
Como\(x→0^+\), el numerador\(\tan x−x^2→0\) y el denominador\(x^2\tan x→0.\) Por lo tanto, podemos aplicar la regla de L'Hôpital. Tomando las derivadas del numerador y el denominador, tenemos
\[\lim_{x→0^+}\dfrac{(\tan x)−x^2}{x^2\tan x}=\lim_{x→0^+}\dfrac{(\sec^2x)−2x}{x^2\sec^2x+2x\tan x}. \nonumber \]
Como\(x→0^+\),\((\sec^2x)−2x→1\) y\(x^2\sec^2x+2x\tan x→0\). Dado que el denominador es positivo a medida que\(x\) se acerca a cero desde la derecha, concluimos que
\[\lim_{x→0^+}\dfrac{(\sec^2x)−2x}{x^2\sec^2x+2x\tan x}=∞. \nonumber \]
Por lo tanto,
\[\lim_{x→0^+}\left(\dfrac{1}{x^2}−\dfrac{1}{\tan x}\right)=∞. \nonumber \]
Evaluar\(\displaystyle \lim_{x→0^+}\left(\dfrac{1}{x}−\dfrac{1}{\sin x}\right)\).
- Pista
-
Reescribir la diferencia de fracciones como una sola fracción.
- Responder
-
0
Otro tipo de forma indeterminada que surge al evaluar límites involucra a los exponentes. Las expresiones\(0^0, ∞^0\), y\(1^∞\) son todas formas indeterminadas. Por sí mismas, estas expresiones carecen de sentido porque en realidad no podemos evaluar estas expresiones como evaluaríamos una expresión que involucra números reales. Más bien, estas expresiones representan formas que surgen al encontrar límites. Ahora examinamos cómo se puede utilizar la regla de L'Hôpital para evaluar los límites que involucran estas formas indeterminadas.
Dado que la regla de L'Hôpital se aplica a los cocientes, utilizamos la función de logaritmo natural y sus propiedades para reducir un problema evaluando un límite que involucra exponentes a un problema relacionado que involucra un límite de un cociente. Por ejemplo, supongamos que queremos evaluar\(\displaystyle \lim_{x→a}f(x)^{g(x)}\) y llegamos a la forma indeterminada\(∞^0\). (Las formas indeterminadas\(0^0\) y\(1^∞\) pueden ser manejadas de manera similar.) Procedemos de la siguiente manera. Let
\[y=f(x)^{g(x)}. \nonumber \]
Entonces,
\[\ln y=\ln(f(x)^{g(x)})=g(x)\ln(f(x)). \nonumber \]
Por lo tanto,
\[\lim_{x→a}[\ln(y)]=\lim_{x→a}[g(x)\ln(f(x))]. \nonumber \]
Ya\(\displaystyle \lim_{x→a}f(x)=∞,\) que sabemos eso\(\displaystyle \lim_{x→a}\ln(f(x))=∞\). Por lo tanto,\(\displaystyle \lim_{x→a}g(x)\ln(f(x))\) es de la forma indeterminada\(0⋅∞\), y podemos utilizar las técnicas discutidas anteriormente para reescribir la expresión\(g(x)\ln(f(x))\) en una forma para que podamos aplicar la regla de L'Hôpital. Supongamos\(\displaystyle \lim_{x→a}g(x)\ln(f(x))=L\), donde\(L\) puede estar\(∞\) o\(−∞.\) Entonces
\[\lim_{x→a}[\ln(y)]=L. \nonumber \]
Dado que la función de logaritmo natural es continua, concluimos que
\[\ln\left(\lim_{x→a}y\right)=L, \nonumber \]
lo que nos da
\[\lim_{x→a}y=\lim_{x→a}f(x)^{g(x)}=e^L. \nonumber \]
Evaluar\[\lim_{x→∞}x^{1/x}. \nonumber \]
Solución
Vamos\(y=x^{1/x}\) .Entonces,
\[\ln(x^{1/x})=\dfrac{1}{x}\ln x=\dfrac{\ln x}{x}. \nonumber \]
Tenemos que evaluar\(\displaystyle \lim_{x→∞}\dfrac{\ln x}{x}\). Aplicando la regla de L'Hôpital, obtenemos
\[\lim_{x→∞}\ln y=\lim_{x→∞}\dfrac{\ln x}{x}=\lim_{x→∞}\dfrac{1/x}{1}=0. \nonumber \]
Por lo tanto,\(\displaystyle \lim_{x→∞}\ln y=0.\) dado que la función de logaritmo natural es continua, concluimos que
\[\ln\left(\lim_{x→∞}y\right)=0, \nonumber \]
lo que lleva a
\[\lim_{x→∞}x^{1/x}=\lim_{x→∞}y=e^{\ln\left(\lim_{x→∞}y\right)}=e^0=1. \nonumber \]
Por lo tanto,
\[\lim_{x→∞}x^{1/x}=1. \nonumber \]
Evaluar\[\lim_{x→∞}x^{1/\ln(x)}. \nonumber \]
- Pista
-
Dejar\(y=x^{1/\ln(x)}\) y aplicar el logaritmo natural a ambos lados de la ecuación.
- Responder
-
\(e\)
Evaluar\[\lim_{x→0^+}x^{\sin x}. \nonumber \]
Solución
Let
\[y=x^{\sin x}. \nonumber \]
Por lo tanto,
\[\ln y=\ln(x^{\sin x})=\sin x\ln x. \nonumber \]
Ahora evaluamos\(\displaystyle\lim_{x→0^+}\sin x\ln x.\) Desde\(\displaystyle\lim_{x→0^+}\sin x=0\) y\(\displaystyle\lim_{x→0^+}\ln x=−∞\), tenemos la forma indeterminada\(0⋅∞\). Para aplicar la regla de L'Hôpital, necesitamos reescribir\(\sin x\ln x\) como fracción. Podríamos escribir
\[\sin x\ln x=\dfrac{\sin x}{1/\ln x} \nonumber \]
o
\[\sin x\ln x=\dfrac{\ln x}{1/\sin x}=\dfrac{\ln x}{\csc x}. \nonumber \]
Consideremos la primera opción. En este caso, aplicando la regla de L'Hôpital, obtendríamos
\[\lim_{x→0^+}\sin x\ln x=\lim_{x→0^+}\dfrac{\sin x}{1/\ln x}=\lim_{x→0^+}\dfrac{\cos x}{−1/(x(\ln x)^2)}=\lim_{x→0^+}(−x(\ln x)^2\cos x).\nonumber \]
Desafortunadamente, no sólo tenemos otra expresión que involucra la forma indeterminada\(0⋅∞,\) sino que el nuevo límite es aún más complicado de evaluar que el con el que empezamos. En cambio, intentamos la segunda opción. Por escrito
\[\sin x\ln x=\dfrac{\ln x}{1/\sin x}=\dfrac{\ln x}{\csc x,} \nonumber \]
y aplicando la regla de L'Hôpital, obtenemos
\[\lim_{x→0^+}\sin x\ln x=\lim_{x→0^+}\dfrac{\ln x}{\csc x}=\lim_{x→0^+}\dfrac{1/x}{−\csc x\cot x}=\lim_{x→0^+}\dfrac{−1}{x\csc x\cot x}. \nonumber \]
Usando el hecho de que\(\csc x=\dfrac{1}{\sin x}\) y\(\cot x=\dfrac{\cos x}{\sin x}\), podemos reescribir la expresión en el lado derecho como
\[\lim_{x→0^+}\dfrac{−\sin^2x}{x\cos x}=\lim_{x→0^+}\left[\dfrac{\sin x}{x}⋅(−\tan x)\right]=\left(\lim_{x→0^+}\dfrac{\sin x}{x}\right)⋅\left(\lim_{x→0^+}(−\tan x)\right)=1⋅0=0. \nonumber \]
Concluimos que\(\displaystyle\lim_{x→0^+}\ln y=0.\) Por lo tanto,\(\displaystyle\ln\left(\lim_{x→0^+}y\right)=0\) y tenemos
\[\lim_{x→0^+}y=\lim_{x→0^+}x^{\sin x}=e^0=1.\nonumber \]
Por lo tanto,
\[\lim_{x→0^+}x^{\sin x}=1. \nonumber \]
Evaluar\(\displaystyle \lim_{x→0^+}x^x\).
- Pista
-
Dejar\(y=x^x\) y tomar el logaritmo natural de ambos lados de la ecuación.
- Responder
-
1
Tasas de crecimiento de las funciones
Supongamos las funciones\(f\) y\(g\) ambas se acercan al infinito como\(x→∞\). Aunque los valores de ambas funciones se vuelven arbitrariamente grandes a medida que los valores de\(x\) llegan a ser suficientemente grandes, a veces una función está creciendo más rápidamente que la otra. Por ejemplo,\(f(x)=x^2\) y\(g(x)=x^3\) ambos se acercan al infinito como\(x→∞\). Sin embargo, como\(\PageIndex{1}\) muestra la Tabla, los valores de\(x^3\) están creciendo mucho más rápido que los valores de\(x^2\).
| \(x\) | 10 | 100 | 1000 | 10,000 |
|---|---|---|---|---|
| \(f(x)=x^2\) | 100 | 10,000 | 1,000,000 | 100,000,000 |
| \(g(x)=x^3\) | 1000 | 1,000,000 | 1,000,000,000 | 1,000,000,000,000 |
De hecho,
\[\lim_{x→∞}\dfrac{x^3}{x^2}=\lim_{x→∞}x=∞. \nonumber \]
o, equivalentemente
\[\lim_{x→∞}\dfrac{x^2}{x^3}=\lim_{x→∞}\dfrac{1}{x}=0. \nonumber \]
Como resultado, decimos que\(x^3\) está creciendo más rápidamente que\(x^2\) como\(x→∞\). Por otro lado, para\(f(x)=x^2\) y\(g(x)=3x^2+4x+1\), aunque los valores de siempre\(g(x)\) son mayores que los valores de\(f(x)\) for\(x>0\), cada valor de\(g(x)\) es aproximadamente tres veces el valor correspondiente de\(f(x)\) as\(x→∞\), como se muestra en la Tabla\(\PageIndex{2}\). De hecho,
\[\lim_{x→∞}\dfrac{x^2}{3x^2+4x+1}=\dfrac{1}{3}. \nonumber \]
| \(x\) | 10 | 100 | 1000 | 10,000 |
|---|---|---|---|---|
| \(f(x)=x^2\) | 100 | 10,000 | 1,000,000 | 100,000,000 |
| \(g(x)=3x^2+4x+1\) | 341 | 30,401 | 3,004,001 | 300,040,001 |
En este caso, decimos eso\(x^2\) y\(3x^2+4x+1\) estamos creciendo al mismo ritmo que\(x→∞.\)
De manera más general, supongamos\(f\) y\(g\) son dos funciones que se acercan al infinito como\(x→∞\). Decimos que\(g\) crece más rápido que\(f\) como\(x→∞\) si
\[\lim_{x→∞}\dfrac{g(x)}{f(x)}=∞ \quad \text{or, equivalently,} \quad \lim_{x→∞}\dfrac{f(x)}{g(x)}=0. \nonumber \]
Por otro lado, si existe una constante\(M≠0\) tal que
\[\lim_{x→∞}\dfrac{f(x)}{g(x)}=M, \nonumber \]
decimos\(f\) y\(g\) crecemos al mismo ritmo que\(x→∞\).
A continuación vemos cómo usar la regla de L'Hôpital para comparar las tasas de crecimiento de las funciones de poder, exponenciales y logarítmicas.
Para cada uno de los siguientes pares de funciones, use la regla de L'Hôpital para evaluar\[\lim_{x→∞}\dfrac{f(x)}{g(x)}. \nonumber \]
- \(f(x)=x^2\)y\(g(x)=e^x\)
- \(f(x)=\ln(x)\)y\(g(x)=x^2\)
Solución
a. desde\(\displaystyle \lim_{x→∞}x^2=∞\) y\(\displaystyle \lim_{x→∞}e^x=∞\), podemos usar la regla de L'Hôpital para evaluar\(\displaystyle \lim_{x→∞}\left[\dfrac{x^2}{e^x}\right]\). Obtenemos
\[\lim_{x→∞}\frac{x^2}{e^x}=\lim_{x→∞}\frac{2x}{e^x}. \nonumber \]
Desde\(\displaystyle \lim_{x→∞}2x=∞\) y\(\displaystyle \lim_{x→∞}e^x=∞\), podemos aplicar nuevamente la regla de L'Hôpital. Desde
\[\lim_{x→∞}\frac{2x}{e^x}=\lim_{x→∞}\frac{2}{e^x}=0, \nonumber \]
concluimos que
\[\lim_{x→∞}\dfrac{x^2}{e^x}=0. \nonumber \]
Por lo tanto,\(e^x\) crece más rápidamente que\(x^2\) como\(x→∞\) (Ver Figura\(\PageIndex{3}\) y Tabla\(\PageIndex{3}\))
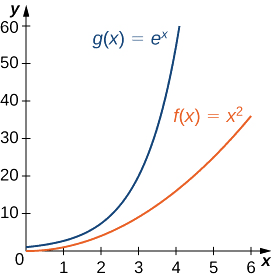
| \(x\) | 5 | 10 | 15 | 20 |
|---|---|---|---|---|
| \(x^2\) | 25 | 100 | 225 | 400 |
| \(e^x\) | 148 | 22,026 | 3,269,017 | 485,165,195 |
b. Desde\(\displaystyle \lim_{x→∞}\ln x=∞\) y\(\displaystyle \lim_{x→∞}x^2=∞\), podemos usar la regla de L'Hôpital para evaluar\(\displaystyle \lim_{x→∞}\dfrac{\ln x}{x^2}\). Obtenemos
\[\lim_{x→∞}\dfrac{\ln x}{x^2}=\lim_{x→∞}\dfrac{1/x}{2x}=\lim_{x→∞}\dfrac{1}{2x^2}=0. \nonumber \]
Así,\(x^2\) crece más rápidamente que\(\ln x\) como\(x→∞\) (ver Figura\(\PageIndex{4}\) y Tabla\(\PageIndex{4}\)).
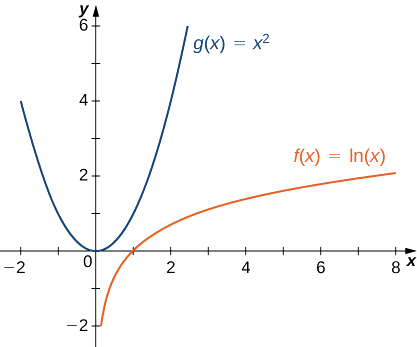
| \(x\) | 10 | 100 | 1000 | 10,000 |
|---|---|---|---|---|
| \(\ln(x)\) | 2.303 | 4.605 | 6.908 | 9.210 |
| \(x^2\) | 100 | 10,000 | 1,000,000 | 100,000,000 |
Comparar las tasas de crecimiento de\(x^{100}\) y\(2^x\).
- Pista
-
Aplicar la regla de L'Hôpital a\(x^{100}/2^x\).
- Responder
-
La función\(2^x\) crece más rápido que\(x^{100}\).
Usando las mismas ideas que en Ejemplo\(\PageIndex{8}a\). no es difícil demostrar que\(e^x\) crece más rápidamente que\(x^p\) para ninguno\(p>0\). En Figura\(\PageIndex{5}\) y Tabla\(\PageIndex{5}\), comparamos\(e^x\) con\(x^3\) y\(x^4\) como\(x→∞\).
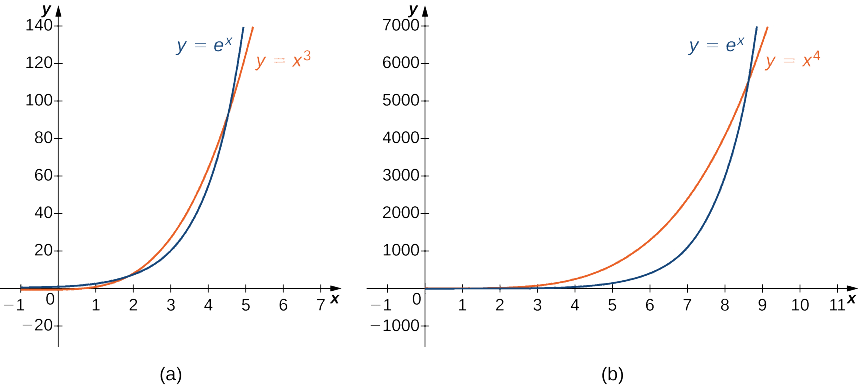
| \(x\) | 5 | 10 | 15 | 20 |
|---|---|---|---|---|
| \(x^3\) | 125 | 1000 | 3375 | 8000 |
| \(x^4\) | 625 | 10,000 | 50,625 | 160,000 |
| \(e^x\) | 148 | 22,026 | 3,269,017 | 485,165,195 |
De igual manera, no es difícil demostrar que\(x^p\) crece más rápidamente que\(\ln x\) para ninguno\(p>0\). En Figura\(\PageIndex{6}\) y Tabla\(\PageIndex{6}\), comparamos\(\ln x\) con\(\sqrt[3]{x}\) y\(\sqrt{x}\).
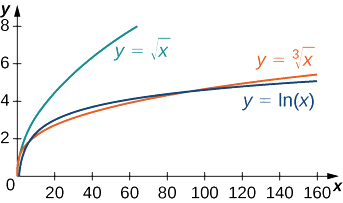
| \(x\) | 10 | 100 | 1000 | 10,000 |
|---|---|---|---|---|
| \(\ln(x)\) | 2.303 | 4.605 | 6.908 | 9.210 |
| \(\sqrt[3]{x}\) | 2.154 | 4.642 | 10 | 21.544 |
| \(\sqrt{x}\) | 3.162 | 10 | 31.623 | 100 |
Conceptos clave
- La regla de L'Hôpital puede utilizarse para evaluar el límite de un cociente cuando surge la forma indeterminada\(\dfrac{0}{0}\) o\(∞/∞\) surge.
- La regla de L'Hôpital también puede aplicarse a otras formas indeterminadas si pueden reescribirse en términos de un límite que implique un cociente que tenga la forma indeterminada\(\dfrac{0}{0}\) o\(∞/∞.\)
- La función exponencial\(e^x\) crece más rápido que cualquier función de potencia\(x^p, p>0\).
- La función logarítmica\(\ln x\) crece más lentamente que cualquier función de potencia\(x^p, p>0\).
Glosario
- formas indeterminadas
- Al evaluar un límite, las formas\(\dfrac{0}{0}\),\(∞/∞, 0⋅∞, ∞−∞, 0^0, ∞^0\), y\(1^∞\) se consideran indeterminadas porque se requiere un mayor análisis para determinar si existe el límite y, de ser así, cuál es su valor.
- La regla de L'Hôpital
- Si\(f\) y\(g\) son funciones diferenciables a lo largo de un intervalo\(a\), excepto posiblemente at\(a\), y\(\displaystyle \lim_{x→a}f(x)=0=\lim_{x→a}g(x)\) o\(\displaystyle \lim_{x→a}f(x)\) y\(\displaystyle \lim_{x→a}g(x)\) son infinitas, entonces\(\displaystyle \lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)}\), asumiendo que el límite a la derecha existe o es\(∞\) o\(−∞\).


