6.9: Cálculo de las Funciones Hiperbólicas
- Page ID
- 116156
- Aplicar las fórmulas para derivadas e integrales de las funciones hiperbólicas.
- Aplicar las fórmulas para las derivadas de las funciones hiperbólicas inversas y sus integrales asociadas.
- Describir las condiciones comunes aplicadas de una curva catenaria.
Anteriormente fuimos introducidos a las funciones hiperbólicas, junto con algunas de sus propiedades básicas. En esta sección, analizamos las fórmulas de diferenciación e integración para las funciones hiperbólicas y sus inversas.
Derivadas e Integrales de las Funciones Hiperbólicas
Recordemos que el seno hiperbólico y el coseno hiperbólico se definen como
\[\sinh x=\dfrac{e^x−e^{−x}}{2} \nonumber \]
y
\[\cosh x=\dfrac{e^x+e^{−x}}{2}. \nonumber \]
Las otras funciones hiperbólicas se definen entonces en términos de\(\sinh x\) y\(\cosh x\). Las gráficas de las funciones hiperbólicas se muestran en la Figura\(\PageIndex{1}\).
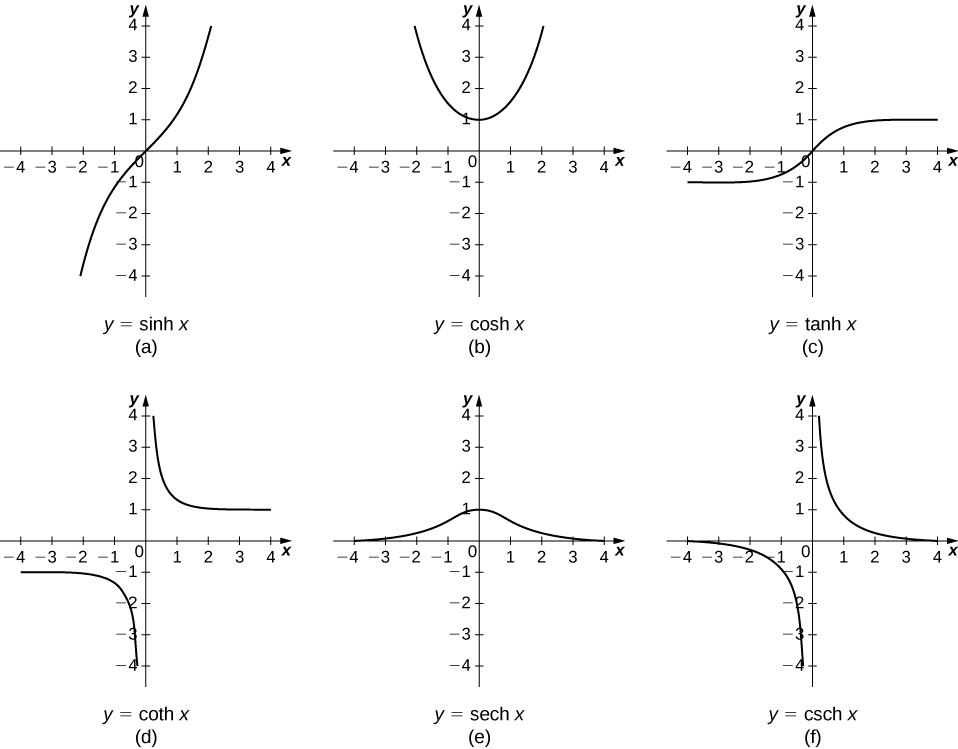
Es fácil desarrollar fórmulas de diferenciación para las funciones hiperbólicas. Por ejemplo, mirando\(\sinh x\) tenemos
\[\begin{align*} \dfrac{d}{dx} \left(\sinh x \right) &=\dfrac{d}{dx} \left(\dfrac{e^x−e^{−x}}{2}\right) \\[4pt] &=\dfrac{1}{2}\left[\dfrac{d}{dx}(e^x)−\dfrac{d}{dx}(e^{−x})\right] \\[4pt] &=\dfrac{1}{2}[e^x+e^{−x}] \\[4pt] &=\cosh x. \end{align*} \nonumber \]
Del mismo modo,
\[\dfrac{d}{dx} \cosh x=\sinh x. \nonumber \]
Resumimos las fórmulas de diferenciación para las funciones hiperbólicas en Table\(\PageIndex{1}\).
| \(f(x)\) | \(\dfrac{d}{dx}f(x)\) |
|---|---|
| \ (f (x)\)” style="text-align:center; ">\(\sinh x\) | \ (\ dfrac {d} {dx} f (x)\)” style="text-align:center; ">\(\cosh x\) |
| \ (f (x)\)” style="text-align:center; ">\(\cosh x\) | \ (\ dfrac {d} {dx} f (x)\)” style="text-align:center; ">\(\sinh x\) |
| \ (f (x)\)” style="text-align:center; ">\(\tanh x\) | \ (\ dfrac {d} {dx} f (x)\)” style="text-align:center; ">\(\text{sech}^2 \,x\) |
| \ (f (x)\)” style="text-align:center; ">\(\text{coth } x\) | \ (\ dfrac {d} {dx} f (x)\)” style="text-align:center; ">\(−\text{csch}^2\, x\) |
| \ (f (x)\)” style="text-align:center; ">\(\text{sech } x\) | \ (\ dfrac {d} {dx} f (x)\)” style="text-align:center; ">\(−\text{sech}\, x \tanh x\) |
| \ (f (x)\)” style="text-align:center; ">\(\text{csch } x\) | \ (\ dfrac {d} {dx} f (x)\)” style="text-align:center; ">\(−\text{csch}\, x \coth x\) |
Tomemos un momento para comparar las derivadas de las funciones hiperbólicas con las derivadas de las funciones trigonométricas estándar. Hay muchas similitudes, pero también diferencias. Por ejemplo, las derivadas de las funciones sinusoidales coinciden con:
\[\dfrac{d}{dx} \sin x=\cos x \nonumber \]
y
\[\dfrac{d}{dx} \sinh x=\cosh x. \nonumber \]
Las derivadas de las funciones coseno, sin embargo, difieren en signo:
\[\dfrac{d}{dx} \cos x=−\sin x, \nonumber \]
pero
\[\dfrac{d}{dx} \cosh x=\sinh x. \nonumber \]
A medida que continuamos nuestro examen de las funciones hiperbólicas, debemos ser conscientes de sus similitudes y diferencias con las funciones trigonométricas estándar. Estas fórmulas de diferenciación para las funciones hiperbólicas conducen directamente a las siguientes fórmulas integrales.
\[ \begin{align} \int \sinh u \,du &=\cosh u+C \\[4pt] \int \text{csch}^2 u \, du &=−\coth u+C \\[4pt] \int \cosh u \,du &=\sinh u+C \\[4pt] \int \text{sech} \,u \tanh u \,du &=−\text{sech } \,u+C−\text{csch} \,u+C \\[4pt] \int \text{sech }^2u \,du &=\tanh u+C \\[4pt] \int \text{csch} \,u \coth u \,du &=−\text{csch} \,u+C \end{align} \nonumber \]
Evaluar los siguientes derivados:
- \(\dfrac{d}{dx}(\sinh(x^2))\)
- \(\dfrac{d}{dx}(\cosh x)^2\)
Solución:
Usando las fórmulas en Tabla\(\PageIndex{1}\) y la regla de la cadena, obtenemos
- \(\dfrac{d}{dx}(\sinh(x^2))=\cosh(x^2)⋅2x\)
- \(\dfrac{d}{dx}(\cosh x)^2=2\cosh x\sinh x\)
Evaluar los siguientes derivados:
- \(\dfrac{d}{dx}(\tanh(x^2+3x))\)
- \(\dfrac{d}{dx}\left(\dfrac{1}{(\sinh x)^2}\right)\)
- Pista
-
Use las fórmulas en Tabla\(\PageIndex{1}\) y aplique la regla de cadena según sea necesario.
- Contestar a
-
\(\dfrac{d}{dx}(\tanh(x^2+3x))=(\text{sech}^2(x^2+3x))(2x+3)\)
- Respuesta b
-
\(\dfrac{d}{dx}\left(\dfrac{1}{(\sinh x)^2}\right)=\dfrac{d}{dx}(\sinh x)^{−2}=−2(\sinh x)^{−3}\cosh x\)
Evalúe las siguientes integrales:
- \( \displaystyle \int x\cosh(x^2)dx\)
- \( \displaystyle \int \tanh x\,dx\)
Solución
Podemos usar\(u\) -sustitución en ambos casos.
a. vamos\(u=x^2\). Entonces,\(du=2x\,dx\) y
\[\begin{align*} \int x\cosh (x^2)dx &=\int \dfrac{1}{2}\cosh u\,du \\[4pt] &=\dfrac{1}{2}\sinh u+C \\[4pt] &=\dfrac{1}{2}\sinh (x^2)+C. \end{align*}\]
b. vamos\(u=\cosh x\). Entonces,\(du=\sinh x\,dx\) y
\[\begin{align*} \int \tanh x \,dx &=\int \dfrac{\sinh x}{\cosh x}\,dx \\[4pt] &=\int \dfrac{1}{u}du \\[4pt] &=\ln|u|+C \\[4pt] &= \ln|\cosh x|+C.\end{align*}\]
Tenga en cuenta que\(\cosh x>0\) para todos\(x\), así podemos eliminar los signos de valor absoluto y obtener
\[\int \tanh x \,dx=\ln(\cosh x)+C. \nonumber \]
Evalúe las siguientes integrales:
- \(\displaystyle \int \sinh^3x \cosh x \,dx\)
- \(\displaystyle \int \text{sech }^2(3x)\, dx\)
- Pista
-
Use las fórmulas anteriores y aplique\(u\) -sustitución según sea necesario.
- Contestar a
-
\(\displaystyle \int \sinh^3x \cosh x \,dx=\dfrac{\sinh^4x}{4}+C\)
- Respuesta b
-
\(\displaystyle \int \text{sech }^2(3x) \, dx=\dfrac{\tanh(3x)}{3}+C\)
Cálculo de funciones hiperbólicas inversas
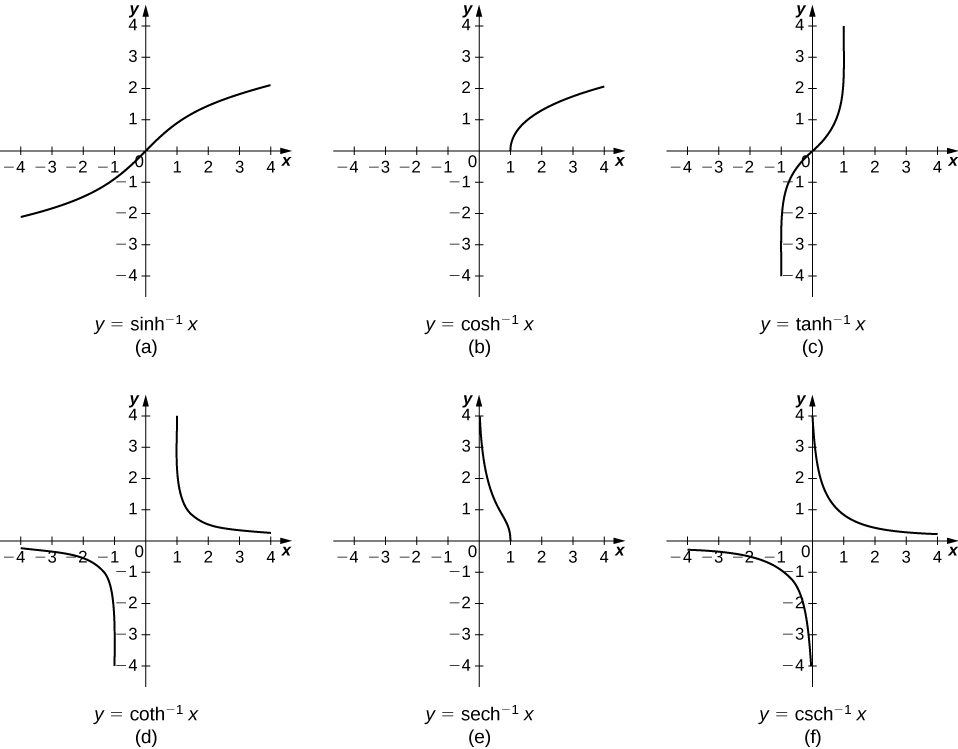
Al observar las gráficas de las funciones hiperbólicas, vemos que con restricciones de rango adecuadas, todas tienen inversas. La mayoría de las restricciones de rango necesarias se pueden discernir mediante un examen minucioso de las gráficas. Los dominios y rangos de las funciones hiperbólicas inversas se resumen en la Tabla\(\PageIndex{2}\).
| Función | Dominio | Rango |
|---|---|---|
| \(\sinh^{−1}x\) | (−∞, ∞) | (−∞, ∞) |
| \(\cosh^{−1}x\) | (1, ∞) | [0, ∞) |
| \(\tanh^{−1}x\) | (−1,1) | (−∞, ∞) |
| \(\coth^{−1}x\) | (−∞ ,1) (1, ∞) | (−∞ ,0) (0, ∞) |
| \(\text{sech}^{−1}x\) | (0,1) | [0, ∞) |
| \(\text{csch}^{−1}x\) | (−∞ ,0) (0, ∞) | (−∞ ,0) (0, ∞) |
Las gráficas de las funciones hiperbólicas inversas se muestran en la siguiente figura.
Para encontrar las derivadas de las funciones inversas, utilizamos diferenciación implícita. Tenemos
\[\begin{align} y &=\sinh^{−1}x \\[4pt] \sinh y &=x \\[4pt] \dfrac{d}{dx} \sinh y &=\dfrac{d}{dx}x \\[4pt] \cosh y\dfrac{dy}{dx} &=1. \end{align} \nonumber \]
Recordemos que\(\cosh^2y−\sinh^2y=1,\) así\(\cosh y=\sqrt{1+\sinh^2y}\) .Entonces,
\[\dfrac{dy}{dx}=\dfrac{1}{\cosh y}=\dfrac{1}{\sqrt{1+\sinh^2y}}=\dfrac{1}{\sqrt{1+x^2}}. \nonumber \]
Podemos derivar fórmulas de diferenciación para las otras funciones hiperbólicas inversas de manera similar. Estas fórmulas de diferenciación se resumen en la Tabla\(\PageIndex{3}\).
| \(f(x)\) | \(\dfrac{d}{dx}f(x)\) |
|---|---|
| \ (f (x)\)” style="vertical-align:middle; ">\(\sinh^{−1}x\) | \ (\ dfrac {d} {dx} f (x)\)” style="vertical-align:middle; ">\(\dfrac{1}{\sqrt{1+x^2}}\) |
| \ (f (x)\)” style="vertical-align:middle; ">\(\cosh^{−1}x\) | \ (\ dfrac {d} {dx} f (x)\)” style="vertical-align:middle; ">\(\dfrac{1}{\sqrt{x^2−1}}\) |
| \ (f (x)\)” style="vertical-align:middle; ">\(\tanh^{−1}x\) | \ (\ dfrac {d} {dx} f (x)\)” style="vertical-align:middle; ">\(\dfrac{1}{1−x^2}\) |
| \ (f (x)\)” style="vertical-align:middle; ">\(\coth^{−1}x\) | \ (\ dfrac {d} {dx} f (x)\)” style="vertical-align:middle; ">\(\dfrac{1}{1−x^2}\) |
| \ (f (x)\)” style="vertical-align:middle; ">\(\text{sech}^{−1}x\) | \ (\ dfrac {d} {dx} f (x)\)” style="vertical-align:middle; ">\(\dfrac{−1}{x\sqrt{1−x^2}}\) |
| \ (f (x)\)” style="vertical-align:middle; ">\(\text{csch}^{−1}x\) | \ (\ dfrac {d} {dx} f (x)\)” style="vertical-align:middle; ">\(\dfrac{−1}{|x|\sqrt{1+x^2}}\) |
Tenga en cuenta que los derivados de\(\tanh^{−1}x\) y\(\coth^{−1}x\) son los mismos. Así, cuando integramos\(1/(1−x^2)\), necesitamos seleccionar el antiderivado adecuado basado en el dominio de las funciones y los valores de\(x\). Las fórmulas de integración que involucran las funciones hiperbólicas inversas se resumen de la siguiente manera.
\[\int \dfrac{1}{\sqrt{1+u^2}}du=\sinh^{−1}u+C \nonumber \]
\[\int \dfrac{1}{u\sqrt{1−u^2}}du=−\text{sech}^{−1}|u|+C \nonumber \]
\[\int \dfrac{1}{\sqrt{u^2−1}}du=\cosh^{−1}u+C \nonumber \]
\[\int \dfrac{1}{u\sqrt{1+u^2}}du=−\text{csch}^{−1}|u|+C \nonumber \]
\[\int \dfrac{1}{1−u^2}du=\begin{cases}\tanh^{−1}u+C & \text{if }|u|<1\\ \coth^{−1}u+C & \text{if }|u|>1\end{cases} \nonumber \]
Evaluar los siguientes derivados:
- \(\dfrac{d}{dx}\left(\sinh^{−1}\left(\dfrac{x}{3}\right)\right)\)
- \(\dfrac{d}{dx}\left(\tanh^{−1}x\right)^2\)
Solución
Usando las fórmulas de Tabla\(\PageIndex{3}\) y la regla de la cadena, obtenemos los siguientes resultados:
- \(\dfrac{d}{dx}(\sinh^{−1}(\dfrac{x}{3}))=\dfrac{1}{3\sqrt{1+\dfrac{x^2}{9}}}=\dfrac{1}{\sqrt{9+x^2}}\)
- \(\dfrac{d}{dx}(\tanh^{−1}x)^2=\dfrac{2(\tanh^{−1}x)}{1−x^2}\)
Evaluar los siguientes derivados:
- \(\dfrac{d}{dx}(\cosh^{−1}(3x))\)
- \(\dfrac{d}{dx}(\coth^{−1}x)^3\)
- Pista
-
Use las fórmulas en Tabla\(\PageIndex{3}\) y aplique la regla de cadena según sea necesario.
- Contestar a
-
\(\dfrac{d}{dx}(\cosh^{−1}(3x))=\dfrac{3}{\sqrt{9x^2−1}} \)
- Respuesta b
-
\(\dfrac{d}{dx}(\coth^{−1}x)^3=\dfrac{3(\coth^{−1}x)^2}{1−x^2} \)
Evalúe las siguientes integrales:
- \(\displaystyle \int \dfrac{1}{\sqrt{4x^2−1}}dx\)
- \(\displaystyle \int \dfrac{1}{2x\sqrt{1−9x^2}}dx\)
Solución
Podemos usar \(u\)-sustitución en ambos casos.
Vamos\(u=2x\). Entonces,\(du=2\,dx\) y tenemos
\[\begin{align*} \int \dfrac{1}{\sqrt{4x^2−1}}\,dx &=\int \dfrac{1}{2\sqrt{u^2−1}}\,du \\[4pt] &=\dfrac{1}{2}\cosh^{−1}u+C \\[4pt] &=\dfrac{1}{2}\cosh^{−1}(2x)+C. \end{align*} \nonumber \]
Vamos\(u=3x.\) Entonces,\(du=3\,dx\) y obtenemos
\[\begin{align*} \int \dfrac{1}{2x\sqrt{1−9x^2}}dx &=\dfrac{1}{2}\int \dfrac{1}{u\sqrt{1−u^2}}du \\[4pt] &=−\dfrac{1}{2}\text{sech}^{−1}|u|+C \\[4pt] &=−\dfrac{1}{2}\text{sech}^{−1}|3x|+C \end{align*}\]
Evalúe las siguientes integrales:
- \(\displaystyle \int \dfrac{1}{\sqrt{x^2−4}}dx,x>2\)
- \(\displaystyle \int \dfrac{1}{\sqrt{1−e^{2x}}}dx\)
- Pista
-
Use las fórmulas anteriores y aplique\(u\) -sustitución según sea necesario.
- Contestar a
-
\(\displaystyle \int \dfrac{1}{\sqrt{x^2−4}}dx=\cosh^{−1}(\dfrac{x}{2})+C\)
- Respuesta b
-
\( \displaystyle \int \dfrac{1}{\sqrt{1−e^{2x}}}dx=−\text{sech}^{−1}(e^x)+C\)
Aplicaciones
Una aplicación física de funciones hiperbólicas implica colgar cables. Si un cable de densidad uniforme se suspende entre dos soportes sin ninguna carga que no sea su propio peso, el cable forma una curva llamada catenaria. Las líneas eléctricas de alto voltaje, las cadenas que cuelgan entre dos postes y las hebras de una tela de araña forman catenarias. En la siguiente figura se muestran cadenas colgadas de una fila de postes.
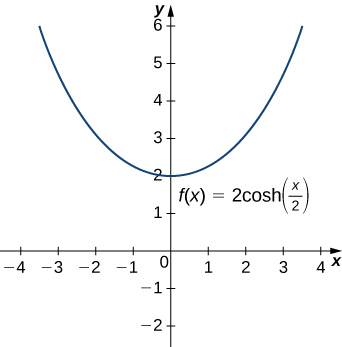
Las funciones hiperbólicas se pueden utilizar para modelar catenarias. Específicamente, las funciones de la forma\(y=a\cdot \cosh(x/a)\) son catenarias. En la figura se\(\PageIndex{4}\) muestra la gráfica de\(y=2\cosh(x/2)\).
Supongamos que un cable colgante tiene la forma\(10\cosh(x/10)\) para\(−15≤x≤15\), donde\(x\) se mide en pies. Determine la longitud del cable (en pies).
Solución
Recordemos de la Sección 6.4 que la fórmula para la longitud del arco es
\[\underbrace{\int ^b_a\sqrt{1+[f′(x)]^2}dx}_{\text{Arc Length}}. \nonumber \]
Tenemos\(f(x)=10 \cosh(x/10)\), entonces\(f′(x)=\sinh(x/10)\). Entonces la longitud del arco es
\[\int ^b_a\sqrt{1+[f′(x)]^2}dx=\int ^{15}_{−15}\sqrt{1+\sinh^2 \left(\dfrac{x}{10}\right)}dx. \nonumber \]
Ahora recordemos que
\[1+\sinh^2x=\cosh^2x, \nonumber \]
por lo que tenemos
\[\begin{align*} \text{Arc Length} &= \int ^{15}_{−15}\sqrt{1+\sinh^2 \left(\dfrac{x}{10}\right)}dx \\[4pt] &=\int ^{15}_{−15}\cosh \left(\dfrac{x}{10}\right)dx \\[4pt] &= \left.10\sinh \left(\dfrac{x}{10}\right)\right|^{15}_{−15}\\[4pt] &=10\left[\sinh\left(\dfrac{3}{2}\right)−\sinh\left(−\dfrac{3}{2}\right)\right]\\[4pt] &=20\sinh \left(\dfrac{3}{2}\right) \\[4pt] &≈42.586\,\text{ft.} \end{align*}\]
Supongamos que un cable colgante tiene la forma\(15 \cosh (x/15)\) para\(−20≤x≤20\). Determine la longitud del cable (en pies).
- Contestar
-
\(52.95\)ft
Conceptos clave
- Las funciones hiperbólicas se definen en términos de funciones exponenciales.
- La diferenciación término a término produce fórmulas de diferenciación para las funciones hiperbólicas. Estas fórmulas de diferenciación dan lugar, a su vez, a fórmulas de integración.
- Con restricciones de rango adecuadas, todas las funciones hiperbólicas tienen inversas.
- La diferenciación implícita produce fórmulas de diferenciación para las funciones hiperbólicas inversas, que a su vez dan lugar a fórmulas de integración.
- Las aplicaciones físicas más comunes de las funciones hiperbólicas son los cálculos que involucran catenarias.
Glosario
- catenaria
- una curva en la forma de la función\(y=a\cdot\cosh(x/a)\) es una catenaria; un cable de densidad uniforme suspendido entre dos soportes asume la forma de una catenaria