6.7E: Ejercicios para la Sección 6.7

En los ejercicios 1 - 3, encuentra la derivada$\dfrac{dy}{dx}$.

1)$y=\ln(2x)$

Contestar

$\dfrac{dy}{dx} = \dfrac{1}{x}$

2)$y=\ln(2x+1)$

3)$y=\dfrac{1}{\ln x}$

Contestar

$\dfrac{dy}{dx} = −\dfrac{1}{x(\ln x)^2}$

En los ejercicios 4 - 5, encuentra la integral indefinida.

4)$\displaystyle ∫\frac{dt}{3t}$

5)$\displaystyle ∫\frac{dx}{1+x}$

Contestar

$\displaystyle ∫\frac{dx}{1+x} = \ln|x+1|+C$

En los ejercicios 6 - 15, encuentra la derivada$\dfrac{dy}{dx}.$ (Puedes usar una calculadora para trazar la función y la derivada para confirmar que es correcta).

6) [T]$y=\dfrac{\ln x}{x}$

7) [T]$y=x\ln x$

Contestar

$\dfrac{dy}{dx} = \ln(x)+1$

8) [T]$y=\log_{10}x$

9) [T]$y=\ln(\sin x)$

Contestar

$\dfrac{dy}{dx} = \cot x$

10) [T]$y=\ln(\ln x)$

11) [T]$y=7\ln(4x)$

Contestar

$\dfrac{dy}{dx} = \frac{7}{x}$

12) [T]$y=\ln\big((4x)^7\big)$

13) [T]$y=\ln(\tan x)$

Contestar

$\dfrac{dy}{dx} = \csc x\sec x$

14) [T]$y=\ln(\tan 3x)$

15) [T]$y=\ln(\cos^2x)$

Contestar

$\dfrac{dy}{dx} = −2\tan x$

En los ejercicios 16 - 25, encuentra la integral definida o indefinida.

16)$\displaystyle ∫^1_0\frac{dx}{3+x}$

17)$\displaystyle ∫^1_0\frac{dt}{3+2t}$

Contestar

$\displaystyle ∫^1_0\frac{dt}{3+2t} = \tfrac{1}{2}\ln\left(\tfrac{5}{3}\right)$

18)$\displaystyle ∫^2_0\frac{x}{x^2+1}\, dx$

19)$\displaystyle ∫^2_0\frac{x^3}{x^2+1}\,dx$

Contestar

$\displaystyle ∫^2_0\frac{x^3}{x^2+1}\,dx = 2−\tfrac{1}{2}\ln(5)$

20)$\displaystyle ∫^e_2\frac{dx}{x\ln x}$

21)$\displaystyle ∫^e_2\frac{dx}{(x\ln x)^2}$

Contestar

$\displaystyle ∫^e_2\frac{dx}{(x\ln x)^2} = \frac{1}{\ln(2)}−1$

22)$\displaystyle ∫\frac{\cos x}{\sin x}\, dx$

23)$\displaystyle ∫^{π/4}_0\tan x\,dx$

Contestar

$\displaystyle ∫^{π/4}_0\tan x\,dx = \tfrac{1}{2}\ln(2)$

24)$\displaystyle ∫\cot(3x)\,dx$

25)$\displaystyle ∫\frac{(\ln x)^2}{x}\, dx$

Contestar

$\displaystyle ∫\frac{(\ln x)^2}{x}\, dx = \tfrac{1}{3}(\ln x)^3$

En los ejercicios 26 - 35, computar$\dfrac{dy}{dx}$ diferenciando$\ln y$.

26)$y=\sqrt{x^2+1}$

27)$y=\sqrt{x^2+1}\sqrt{x^2−1}$

Contestar

$\dfrac{dy}{dx} = \dfrac{2x^3}{\sqrt{x^2+1}\sqrt{x^2−1}}$

28)$y=e^{\sin x}$

29)$y=x^{−1/x}$

Contestar

$\dfrac{dy}{dx} = x^{−2−(1/x)}(\ln x−1)$

30)$y=e^{ex}$

31)$y=x^e$

Contestar

$\dfrac{dy}{dx} = ex^{e−1}$

32)$y=x^{(ex)}$

33)$y=\sqrt{x}\sqrt[3]{x}\sqrt[6]{x}$

Contestar

$\dfrac{dy}{dx} = 1$

34)$y=x^{−1/\ln x}$

35)$y=e^{−\ln x}$

Contestar

$\dfrac{dy}{dx} = −\dfrac{1}{x^2}$

En los ejercicios 36 - 40, evaluar por cualquier método.

36)$\displaystyle ∫^{10}_5\dfrac{dt}{t}−∫^{10x}_{5x}\dfrac{dt}{t}$

37)$\displaystyle ∫^{e^π}_1\dfrac{dx}{x}+∫^{−1}_{−2}\dfrac{dx}{x}$

Contestar

$π−\ln(2)$

38)$\dfrac{d}{dx}\left[\displaystyle ∫^1_x\dfrac{dt}{t}\right]$

39)$\dfrac{d}{dx}\left[\displaystyle ∫^{x^2}_x\dfrac{dt}{t}\right]$

Contestar

$\dfrac{1}{x}$

40)$\dfrac{d}{dx}\Big[\ln(\sec x+\tan x)\Big]$

En los ejercicios 41 - 44, usa la función$\ln x$. Si no puede encontrar puntos de intersección analíticamente, use una calculadora.

41) Encontrar el área de la región encerrada por$x=1$ y por$y=5$ encima$y=\ln x$.

Contestar

$(e^5−6)\text{ units}^2$

42) [T] Encuentra la longitud del arco de$\ln x$ desde$x=1$ hasta$x=2$.

43) Encuentra el área entre$\ln x$ y el$x$ eje de$x=1$ a$x=2$.

Contestar

$\ln(4)−1) \text{ units}^2$

44) Encuentra el volumen de la forma creada al girar esta curva de$x=1$ a$x=2$ alrededor del$x$ eje, como se muestra aquí.

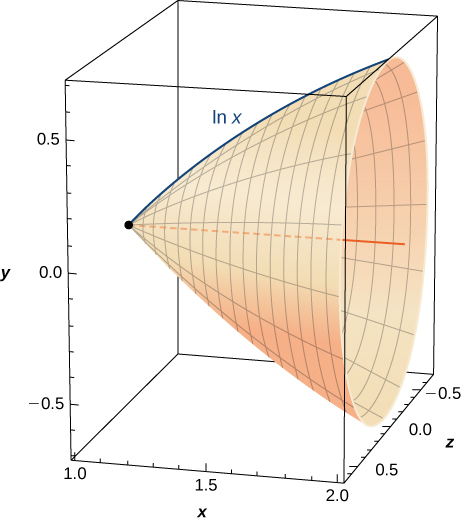
45) [T] Encuentra el área de superficie de la forma creada al girar la curva en el ejercicio anterior de$x=1$ a$x=2$ alrededor del$x$ eje.

Contestar

$2.8656 \text{ units}^2$

Si no puedes encontrar puntos de intersección analíticamente en los siguientes ejercicios, usa una calculadora.

46) Encuentra el área del cuarto de círculo hiperbólico encerrado por$x=2$ y$y=2$ arriba$y=1/x.$

47) [T] Encuentra la longitud del arco de$y=1/x$ desde$x=1$ hasta$x=4$.

Contestar

$s = 3.1502$unidades

48) Encuentra el área debajo$y=1/x$ y por encima del$x$ eje -desde$x=1$ hasta$x=4$.

En los ejercicios 49 - 53, verificar los derivados y antiderivados.

49)$\dfrac{d}{dx}\Big[\ln(x+\sqrt{x^2+1})\Big]=\dfrac{1}{\sqrt{1+x^2}}$

50)$\dfrac{d}{dx}\Big[\ln\left(\frac{x−a}{x+a}\right)\Big]=\dfrac{2a}{(x^2−a^2)}$

51)$\dfrac{d}{dx}\Big[\ln\left(\frac{1+\sqrt{1−x^2}}{x}\right)\Big]=−\dfrac{1}{x\sqrt{1−x^2}}$

52)$\dfrac{d}{dx}\Big[\ln(x+\sqrt{x^2−a^2})\Big]=\dfrac{1}{\sqrt{x^2−a^2}}$

53)$\displaystyle ∫\frac{dx}{x\ln(x)\ln(\ln x)}=\ln|\ln(\ln x)|+C$

Colaboradores

Template:ContribOpenStaxCalc