7.1E: Ejercicios para la Sección 7.1

Al utilizar la técnica de integración por partes, se debe elegir cuidadosamente qué expresión es$u$. Para cada uno de los siguientes problemas, utilice las pautas de esta sección para elegir$u$. No evaluar las integrales.

1)$\displaystyle ∫x^3e^{2x}\,dx$

Contestar

$u=x^3$

2)$\displaystyle ∫x^3\ln(x)\,dx$

3)$\displaystyle ∫y^3\cos y\,dy$

Contestar

$u=y^3$

4)$\displaystyle ∫x^2\arctan x\,dx$

5)$\displaystyle ∫e^{3x}\sin(2x)\,dx$

Contestar

$u=\sin(2x)$

En los ejercicios 6 - 37, encuentra la integral utilizando el método más simple. No todos los problemas requieren integración por partes.

6)$\displaystyle ∫v\sin v\,dv$

7)$\displaystyle ∫\ln x\,dx$ (Pista:$\displaystyle ∫\ln x\,dx$ es equivalente a$\displaystyle ∫1⋅\ln(x)\,dx.)$

Contestar

$\displaystyle ∫\ln x\,dx \quad = \quad−x+x\ln x+C$

8)$\displaystyle ∫x\cos x\,dx$

9)$\displaystyle ∫\tan^{−1}x\,dx$

Contestar

$\displaystyle ∫\tan^{−1}x\,dx\quad = \quad x\tan^{−1}x−\tfrac{1}{2}\ln(1+x^2)+C$

10)$\displaystyle ∫x^2e^x\,dx$

11)$\displaystyle ∫x\sin(2x)\,dx$

Contestar

$\displaystyle ∫x\sin(2x)\,dx \quad = \quad −\tfrac{1}{2}x\cos(2x)+\tfrac{1}{4}\sin(2x)+C$

12)$\displaystyle ∫xe^{4x}\,dx$

13)$\displaystyle ∫xe^{−x}\,dx$

Contestar

$\displaystyle ∫xe^{−x}\,dx \quad = \quad e^{−x}(−1−x)+C$

14)$\displaystyle ∫x\cos 3x\,dx$

15)$\displaystyle ∫x^2\cos x\,dx$

Contestar

$\displaystyle ∫x^2\cos x\,dx \quad = \quad 2x\cos x+(−2+x^2)\sin x+C$

16)$\displaystyle ∫x\ln x\,dx$

17)$\displaystyle ∫\ln(2x+1)\,dx$

Contestar

$\displaystyle ∫\ln(2x+1)\,dx \quad = \quad \tfrac{1}{2}(1+2x)(−1+\ln(1+2x))+C$

18)$\displaystyle ∫x^2e^{4x}\,dx$

19)$\displaystyle ∫e^x\sin x\,dx$

Contestar

$\displaystyle ∫e^x\sin x\,dx \quad = \quad \tfrac{1}{2}e^x(−\cos x+\sin x)+C$

20)$\displaystyle ∫e^x\cos x\,dx$

21)$\displaystyle ∫xe^{−x^2}\,dx$

Contestar

$\displaystyle ∫xe^{−x^2}\,dx \quad = \quad −\frac{e^{−x^2}}{2}+C$

22)$\displaystyle ∫x^2e^{−x}\,dx$

23)$\displaystyle ∫\sin(\ln(2x))\,dx$

Contestar

$\displaystyle ∫\sin(\ln(2x))\,dx \quad = \quad −\tfrac{1}{2}x\cos[\ln(2x)]+\tfrac{1}{2}x\sin[\ln(2x)]+C$

24)$\displaystyle ∫\cos(\ln x)\,dx$

25)$\displaystyle ∫(\ln x)^2\,dx$

Contestar

$\displaystyle ∫(\ln x)^2\,dx \quad = \quad 2x−2x\ln x+x(\ln x)^2+C$

26)$\displaystyle ∫\ln(x^2)\,dx$

27)$\displaystyle ∫x^2\ln x\,dx$

Contestar

$\displaystyle ∫x^2\ln x\,dx \quad = \quad −\frac{x^3}{9}+\tfrac{1}{3}x^3\ln x+C$

28)$\displaystyle ∫\sin^{−1}x\,dx$

29)$\displaystyle ∫\cos^{−1}(2x)\,dx$

Contestar

$\displaystyle ∫\cos^{−1}(2x)\,dx \quad = \quad −\tfrac{1}{2}\sqrt{1−4x^2}+x\cos^{−1}(2x)+C$

30)$\displaystyle ∫x\arctan x\,dx$

31)$\displaystyle ∫x^2\sin x\,dx$

Contestar

$\displaystyle ∫x^2\sin x\,dx \quad = \quad −(−2+x^2)\cos x+2x\sin x+C$

32)$\displaystyle ∫x^3\cos x\,dx$

33)$\displaystyle ∫x^3\sin x\,dx$

Contestar

$\displaystyle ∫x^3\sin x\,dx \quad = \quad −x(−6+x^2)\cos x+3(−2+x^2)\sin x+C$

34)$\displaystyle ∫x^3e^x\,dx$

35)$\displaystyle ∫x\sec^{−1}x\,dx$

Contestar

$\displaystyle ∫x\sec^{−1}x\,dx \quad = \quad \tfrac{1}{2}x\left(−\sqrt{1−\frac{1}{x^2}}+x⋅\sec^{−1}x\right)+C$

36)$\displaystyle ∫x\sec^2x\,dx$

37)$\displaystyle ∫x\cosh x\,dx$

Contestar

$\displaystyle ∫x\cosh x\,dx \quad = \quad −\cosh x+x\sinh x+C$

En los ejercicios 38 - 46, computar las integrales definidas. Utilice una utilidad gráfica para confirmar sus respuestas.

38)$\displaystyle ∫^1_{1/e}\ln x\,dx$

39)$\displaystyle ∫^1_0xe^{−2x}\,dx$ (Exprese la respuesta en forma exacta.)

Contestar

$\displaystyle ∫^1_0xe^{−2x}\,dx \quad = \quad \frac{1}{4}−\frac{3}{4e^2}$

40)$\displaystyle ∫^1_0e^{\sqrt{x}}\,dx \quad (\text{let}\, u=\sqrt{x})$

41)$\displaystyle ∫^e_1\ln(x^2)\,dx$

Contestar

$\displaystyle ∫^e_1\ln(x^2)\,dx \quad = \quad 2$

42)$\displaystyle ∫^π_0x\cos x\,dx$

43)$\displaystyle ∫^π_{−π}x\sin x\,dx$ (Exprese la respuesta en forma exacta.)

Contestar

$\displaystyle ∫^π_{−π}x\sin x\,dx \quad = \quad 2\pi$

44)$\displaystyle ∫^3_0\ln(x^2+1)\,dx$ (Exprese la respuesta en forma exacta.)

45)$\displaystyle ∫^{π/2}_0x^2\sin x\,dx$ (Exprese la respuesta en forma exacta.)

Contestar

$\displaystyle ∫^{π/2}_0x^2\sin x\,dx \quad = \quad −2+π$

46)$\displaystyle ∫^1_0x5^x\,dx$ (Exprese la respuesta usando cinco dígitos significativos.)

47) Evaluar$\displaystyle ∫\cos x\ln(\sin x)\,dx$

Contestar

$\displaystyle ∫\cos x\ln(\sin x)\,dx \quad = \quad −\sin(x)+\ln[\sin(x)]\sin x+C$

En los ejercicios 48 - 50, derivar las siguientes fórmulas utilizando la técnica de integración por partes. Supongamos que$n$ es un entero positivo. Estas fórmulas se denominan fórmulas de reducción porque el exponente en el$x$ término se ha reducido en uno en cada caso. La segunda integral es más simple que la integral original.

48)$\displaystyle ∫x^ne^x\,dx=x^ne^x−n∫x^{n−1}e^x\,dx$

49)$\displaystyle ∫x^n\cos x\,dx=x^n\sin x−n∫x^{n−1}\sin x\,dx$

Contestar

Las respuestas varían

50)$\displaystyle ∫x^n\sin x\,dx=$ ______

51) Integrar$\displaystyle ∫2x\sqrt{2x−3}\,dx$ usando dos métodos:

a. Usando piezas, dejando$dv=\sqrt{2x−3}\,dx$

b. Sustitución, dejar$u=2x−3$

Contestar

a.$\displaystyle ∫2x\sqrt{2x−3}\,dx \quad = \quad \tfrac{2}{5}(1+x)(−3+2x)^{3/2}+C$
b.$\displaystyle ∫2x\sqrt{2x−3}\,dx \quad = \quad \tfrac{2}{5}(1+x)(−3+2x)^{3/2}+C$

En los ejercicios 52 - 57, indique si utilizaría la integración por partes para evaluar la integral. Si es así, identificar$u$ y$dv$. Si no es así, describa la técnica utilizada para realizar la integración sin realmente hacer el problema.

52)$\displaystyle ∫x\ln x\,dx$

53)$\displaystyle ∫\frac{\ln^2x}{x}\,dx$

Contestar

No utilice integración por partes. Elige$u$ ser$\ln x$, y la integral es de la forma$\displaystyle ∫u^2\,du.$

54)$\displaystyle ∫xe^x\,dx$

55)$\displaystyle ∫xe^{x^2−3}\,dx$

Contestar

No utilice integración por partes. Dejar$u=x^2−3$, y la integral se puede poner en la forma$∫e^u\,du$.

56)$\displaystyle ∫x^2\sin x\,dx$

57)$\displaystyle ∫x^2\sin(3x^3+2)\,dx$

Contestar

No utilice integración por partes. Elige$u$ ser$u=3x^3+2$ y la integral se puede poner en la forma$\displaystyle ∫\sin(u)\,du.$

En los ejercicios 58-59, esboza la región delimitada arriba por la curva, el$x$ eje -y$x=1$, y encuentra el área de la región. Proporcionar la forma exacta o respuestas redondas al número de lugares indicados.

58)$y=2xe^{−x}$ (Respuesta aproximada a cuatro decimales.)

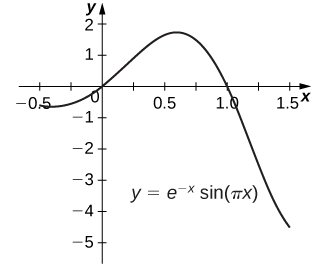
59)$y=e^{−x}\sin(πx)$ (Respuesta aproximada a cinco decimales.)

Contestar

El área debajo de la gráfica es$0.39535 \, \text{units}^2.$

En los ejercicios 60 - 61, encuentra el volumen generado al rotar la región delimitada por las curvas dadas alrededor de la línea especificada. Exprese las respuestas en forma exacta o aproximada al número de decimales indicados.

60)$y=\sin x,\,y=0,\,x=2π,\,x=3π;$ sobre el$y$ eje -( Exprese la respuesta en forma exacta.)

61)$y=e^{−x}, \,y=0,\,x=−1, \, x=0;$ sobre$x=1$ (Exprese la respuesta en forma exacta.)

Contestar

$V = 2πe \, \text{units}^3$

62) Una partícula que se mueve a lo largo de una línea recta tiene una velocidad de$v(t)=t^2e^{−t}$ después de$t$ segundos. ¿Qué tan lejos viaja en los primeros 2 seg? (Supongamos que las unidades están en pies y expresa la respuesta en forma exacta.)

63) Encuentra el área bajo la gráfica de$y=\sec^3x$ de$x=0$ a$x=1$. (Redondear la respuesta a dos dígitos significativos.)

Contestar

$A= 2.05 \, \text{units}^2$

64) Encuentra el área entre$y=(x−2)e^x$ y el$x$ eje de$x=2$ a$x=5$. (Exprese la respuesta en forma exacta.)

65) Encuentra el área de la región encerrada por la curva$y=x\cos x$ y el$x$ eje para$\frac{11π}{2}≤x≤\frac{13π}{2}.$ (Exprese la respuesta en forma exacta.)

Contestar

$A = 12π \, \text{units}^2$

66) Encuentra el volumen del sólido generado al girar la región delimitada por la curva$y=\ln x$, el$x$ eje -y la línea vertical$x=e^2$ alrededor del$x$ eje. (Exprese la respuesta en forma exacta.)

67) Encontrar el volumen del sólido generado al girar la región delimitada por la curva$y=4\cos x$ y el $x$eje -,$\frac{π}{2}≤x≤\frac{3π}{2},$ alrededor del$x$ eje -eje. (Exprese la respuesta en forma exacta.)

Contestar

$V = 8π^2 \, \text{units}^3$

68) Encontrar el volumen del sólido generado al girar la región en el primer cuadrante delimitado por$y=e^x$ y el$x$ eje -eje, desde$x=0$ hasta$x=\ln(7)$, alrededor del$y$ eje -eje. (Exprese la respuesta en forma exacta.)

69) ¿Cuál es el volumen de la torta Bundt que viene de girar$y=\sin x$ alrededor del$y$ eje de$x=0$ a$x=π$?

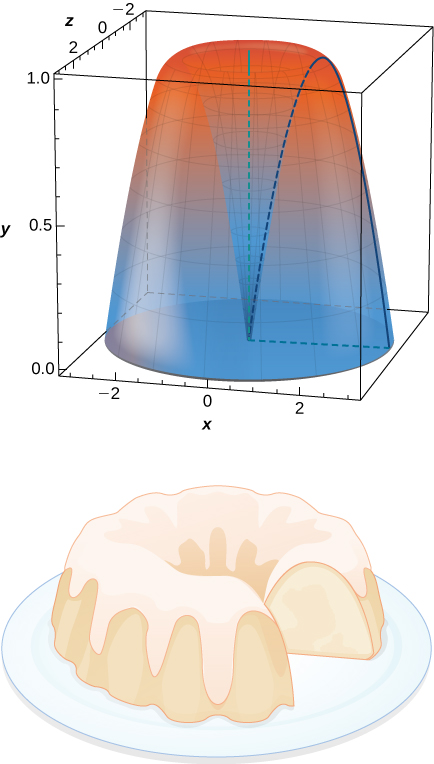
Contestar

$V = 2π^2$unidades ³