7.3: Sustitución trigonométrica

Última actualización
Guardar como PDF

Page ID: 116358

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Resolver problemas de integración que involucran la raíz cuadrada de una suma o diferencia de dos cuadrados.

En esta sección, exploramos integrales que contienen expresiones de la forma\(\sqrt{a^2−x^2}\)\(\sqrt{a^2+x^2}\), y\(\sqrt{x^2−a^2}\), donde los valores de\(a\) son positivos. Ya hemos encontrado y evaluado integrales que contienen algunas expresiones de este tipo, pero muchas siguen siendo inaccesibles. La técnica de sustitución trigonométrica resulta muy útil a la hora de evaluar estas integrales. Esta técnica utiliza la sustitución para reescribir estas integrales como integrales trigonométricas.

Integrales que involucran\(\sqrt{a^2−x^2}\)

Antes de desarrollar una estrategia general para integrales que contengan\(\sqrt{a^2−x^2}\), considere la integral\(\displaystyle ∫\textstyle\sqrt{9−x^2}dx.\) Esta integral no puede ser evaluada utilizando ninguna de las técnicas que hemos discutido hasta ahora. No obstante, si hacemos la sustitución\(x=3\sin θ\), tenemos\(dx=3\cos θ \, dθ.\) Después de sustituir en la integral, tenemos

\[ ∫\sqrt{9−x^2}\,dx=∫\textstyle\sqrt{ 9−(3\sin θ)^2}\cdot 3\cos θ \,dθ. \nonumber \]

Después de simplificar, tenemos

\[ ∫\sqrt{ 9−x^2}\,dx=∫ 9\textstyle\sqrt{1−\sin^2θ}\cdot\cos θ \, dθ. \nonumber \]

Dejando\(1−\sin^2θ=\cos^2θ,\) que ahora tengamos

\[ ∫\sqrt{ 9−x^2}\,dx=∫ 9\textstyle\sqrt{\cos^2θ}\cos θ \, dθ. \nonumber \]

Suponiendo que\(\cos θ≥0\), tenemos

\[ ∫\textstyle\sqrt{ 9−x^2}\,dx=∫ 9\cos^2θ \, dθ. \nonumber \]

En este punto, podemos evaluar la integral utilizando las técnicas desarrolladas para integrar potencias y productos de funciones trigonométricas. Antes de completar este ejemplo, echemos un vistazo a la teoría general detrás de esta idea.

Para evaluar integrales que involucren\(\sqrt{a^2−x^2}\), hacemos la sustitución\(x=a\sin θ\) y\(dx=a\cos θ\). Para ver que esto realmente tiene sentido, considere el siguiente argumento: El dominio de\(\sqrt{a^2−x^2}\) es\([−a,a]\). Así,

\[−a≤x≤a. \nonumber \]

En consecuencia,

\[−1≤\dfrac{x}{a}≤1. \nonumber \]

Dado que el rango de\(\sin x\) más\([−(π/2),π/2]\) es\([−1,1]\), hay un ángulo único\(θ\) satisfactorio\(−(π/2)≤θ≤π/2\) para que\(\sin θ=x/a\), o equivalentemente, para que\(x=a\sin θ\). Si sustituimos\(x=a\sin θ\) en\(\sqrt{a^2−x^2}\), obtenemos

\ [\ begin {align*}\ sqrt {a^2−x^2} &=\ sqrt {a^2− (a\ sin θ) ^2} & &\ text {Dejar} x=a\ sin θ\ texto {donde} −\ dfrac {π} {2} ≤θ≤\ dfrac {π} {2}.\\ [4pt]
& &\ texto {Simplificar.}\\ [4pt]
&=\ sqrt {a^2−a^2\ sen ^2θ} & &\ text {Factor de salida} a^2.\\ [4pt]
&=\ sqrt {a^2 (1−\ sin^2θ)} & &\ text {Sustituto} 1−\ sin^2x=\ cos^2x.\\ [4pt]
&=\ sqrt {a^2\ cos^2θ} & &\ text {Toma la raíz cuadrada.}\\ [4pt]
&=|a\ cos θ|\\ [4pt]
&=a\ cos\ θ final {alinear*}\]

Ya que\(\cos x≥0\) el\(−\dfrac{π}{2}≤θ≤\dfrac{π}{2}\) y\(a>0, |a\cos θ|=a\cos θ.\) Podemos ver, a partir de esta discusión, que al hacer la sustitución\(x=a\sin θ\), somos capaces de convertir una integral que involucra a un radical en una integral que involucra funciones trigonométricas. Después de evaluar la integral, podemos convertir la solución de nuevo en una expresión que involucra\(x\). Para ver cómo hacer esto, comencemos asumiendo eso\(0<x<a\). En este caso,\(0<θ<\dfrac{π}{2}\). Ya que\(\sin θ=\dfrac{x}{a}\), podemos dibujar el triángulo de referencia en la Figura\(\PageIndex{1}\) para ayudar a expresar los valores de\(\cos θ, \, \tan θ,\) y las funciones trigonométricas restantes en términos de x, se puede demostrar que este triángulo realmente produce los valores correctos de las funciones trigonométricas evaluadas en\(θ\) para todos\(θ\) satisfactorios\(−\dfrac{π}{2}≤θ≤\dfrac{π}{2}\). Es útil observar que la expresión\(\sqrt{a^2−x^2}\) en realidad aparece como la longitud de un lado del triángulo. Por último, debe\(θ\) aparecer por sí mismo, utilizamos\(θ=\sin^{−1}\left(\dfrac{x}{a}\right).\)

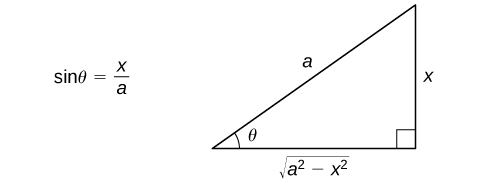
Esta figura es un triángulo rectángulo. Tiene un ángulo etiquetado theta. Este ángulo es opuesto al lado vertical. La hipotenusa está etiquetada como a, la pata vertical está etiquetada con x y la pata horizontal se etiqueta como la raíz cuadrada de (a^2 — x^2). A la izquierda del triángulo está la ecuación sin (theta) = x/a. — Figura\(\PageIndex{1}\): Un triángulo de referencia puede ayudar a expresar las funciones trigonométricas evaluadas\(θ\) en términos de\(x\).

La parte esencial de esta discusión se resume en la siguiente estrategia de resolución de problemas.

Estrategia de resolución de problemas: integración de expresiones que involucran\(\sqrt{a^2−x^2}\)

Es una buena idea asegurarse de que la integral no pueda ser evaluada fácilmente de otra manera. Por ejemplo, aunque este método se puede aplicar a integrales de la forma\(\displaystyle ∫\dfrac{1}{\sqrt{a^2−x^2}}dx\),\(\displaystyle ∫\dfrac{x}{\sqrt{a^2−x^2}}dx,\) y cada una de\(\displaystyle ∫x\sqrt{a^2−x^2}\,dx,\) ellas puede integrarse directamente ya sea por fórmula o por una simple\(u\) -sustitución.
Hacer la sustitución\(x=a \sin θ\) y\(dx=a\cos θ \,dθ.\) Nota: Esta sustitución rinde\(\sqrt{a^2−x^2}=a\cos θ.\)
Simplifica la expresión.
Evaluar la integral utilizando técnicas de la sección sobre integrales trigonométricas.
Utilice el triángulo de referencia de la Figura 1 para reescribir el resultado en términos de\(x\). También es posible que necesites usar algunas identidades trigonométricas y la relación\(θ=\sin^{−1}\left(\dfrac{x}{a}\right).\)

El siguiente ejemplo demuestra la aplicación de esta estrategia de resolución de problemas.

Ejemplo\(\PageIndex{1}\): Integrating an Expression Involving \(\sqrt{a^2−x^2}\)

Evaluar

\[ ∫\sqrt{ 9−x^2}dx. \nonumber \]

Solución

Empezar por hacer las sustituciones\(x=3\sin θ\) y\(dx=3\cos θ \, dθ.\) Desde\(\sin θ=\dfrac{x}{3}\), podemos construir el triángulo de referencia que se muestra en la Figura 2.

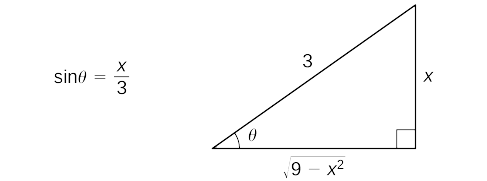
Así,

\[ ∫\sqrt{9−x^2}\,dx=∫\sqrt{ 9−(3\sin θ)^2}3\cos θ\,dθ \nonumber \]

Sustituto\(x=3\sin θ\) y\(dx=3\cos θ \,dθ\).

\(=∫\sqrt{ 9(1−\sin^2θ)}\cdot 3\cos θ \, dθ\)Simplificar.

\(=∫\sqrt{ 9\cos^2θ}\cdot 3\cos θ \, dθ\)Sustituto\(\cos^2θ=1−\sin^2θ\).

\(=∫ 3|\cos θ|3\cos θ \, dθ\)Toma la raíz cuadrada.

\(=∫ 9\cos^2θ \, dθ\)Simplificar. Desde\(−\dfrac{π}{2}≤θ≤\dfrac{π}{2},\cos θ≥0\) y\(|\cos θ|=\cos θ.\)

\(=∫ 9\left(\dfrac{1}{2}+\dfrac{1}{2}\cos(2θ)\right)\,dθ\)Utilice la estrategia para integrar un poder par de\(\cos θ\).

\(=\dfrac{9}{2}θ+\dfrac{9}{4}\sin(2θ)+C\)Evaluar la integral.

\(=\dfrac{9}{2}θ+\dfrac{9}{4}(2\sin θ\cos θ)+C\)

Sustituto\(\sin(2θ)=2\sin θ\cos θ\).

\(=\dfrac{9}{2}\sin^{−1}\left(\dfrac{x}{3}\right)+\dfrac{9}{2}⋅\dfrac{x}{3}⋅\dfrac{\sqrt{9−x^2}}{3}+C\)Sustituto\(\sin^{−1}\left(\dfrac{x}{3}\right)=θ\) y\(\sin θ=\frac{x}{3}\). Usa el triángulo de referencia para ver eso\(\cos θ=\dfrac{\sqrt{9−x^2}}{3} \) y haz esta sustitución. Simplificar.

\(=\dfrac{9}{2}\sin^{−1}\left(\dfrac{x}{3}\right)+\dfrac{x\sqrt{9−x^2}}{2}+C.\)Simplificar.

Ejemplo\(\PageIndex{2}\): Integrating an Expression Involving \(\sqrt{a^2−x^2}\)

Evaluar

\[ ∫\dfrac{\sqrt{4−x^2}}{x}dx. \nonumber \]

Solución

Primero hacer las sustituciones\(x=2\sin θ\) y\(dx=2\cos θ\,dθ\). Ya que\(\sin θ=\dfrac{x}{2}\), podemos construir el triángulo de referencia que se muestra en la Figura\(\PageIndex{3}\).

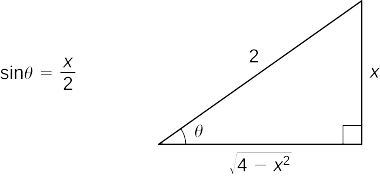
Esta figura es un triángulo rectángulo. Tiene un ángulo etiquetado theta. Este ángulo es opuesto al lado vertical. La pata vertical está etiquetada como x, y la pata horizontal está etiquetada como la raíz cuadrada de (4 — x^2). A la izquierda del triángulo está la ecuación sin (theta) = x/2. — Figura\(\PageIndex{3}\): Se puede construir un triángulo de referencia para Ejemplo\(\PageIndex{2}\).

Así,

\(∫\dfrac{\sqrt{4−x^2}}{x}dx=∫\dfrac{\sqrt{4−(2\sin θ)^2}}{2\sin θ}2\cos θ \, dθ\)Sustituto\(x=2\sin θ\) y\(dx=2\cos θ\,dθ.\)

\(=∫\dfrac{2\cos^2θ}{\sin θ}\,dθ\)Sustituir\(\cos^2θ=1−\sin^2θ\) y simplificar.

\(=∫\dfrac{2(1−\sin^2θ)}{\sin θ}\,dθ\)Sustituto\(\cos^2θ=1−\sin^2θ\).

\(=∫ (2\csc θ−2\sin θ)\,dθ\)Separe el numerador, simplifique y use\(\csc θ=\dfrac{1}{\sin θ}\).

\(=2 \ln |\csc θ−\cot θ|+2\cos θ+C\)Evaluar la integral.

\(=2 \ln \left|\dfrac{2}{x}−\dfrac{\sqrt{4−x^2}}{x}\right|+\sqrt{4−x^2}+C.\)Utilice el triángulo de referencia para reescribir la expresión en términos de\(x\) y simplificar.

En el siguiente ejemplo, vemos que a veces tenemos una opción de métodos.

Ejemplo\(\PageIndex{3}\): Integrating an Expression Involving \(\sqrt{a^2−x^2}\) Two Ways

Evaluar\(∫ x^3\sqrt{1−x^2}dx\) dos formas: primero usando la sustitución\(u=1−x^2\) y luego usando una sustitución trigonométrica.

Método 1

Vamos\(u=1−x^2\) y por lo tanto\(x^2=1−u\). Así,\(du=−2x\,dx.\) en este caso, la integral se convierte

\(∫ x^3\sqrt{1−x^2}\,dx=−\dfrac{1}{2}∫ x^2\sqrt{1−x^2}(−2x\,dx)\)Hacer la sustitución.

\(=−\dfrac{1}{2}∫ (1−u)\sqrt{u}\,du\)Expandir la expresión.

\(=−\dfrac{1}{2}∫(u^{1/2}−u^{3/2})\,du\)Evaluar la integral.

\(=−\dfrac{1}{2}(\dfrac{2}{3}u^{3/2}−\dfrac{2}{5}u^{5/2})+C\)Reescribir en términos de x.

\(=−\dfrac{1}{3}(1−x^2)^{3/2}+\dfrac{1}{5}(1−x^2)^{5/2}+C.\)

Método 2

Vamos\(x=\sin θ\). En este caso,\(dx=\cos θ \, dθ.\) Usando esta sustitución, tenemos

\(∫ x^3\sqrt{1−x^2}dx=∫ \sin^3θ\cos^2θ \, dθ\)

\(=∫ (1−\cos^2θ)\cos^2θ\sin θ \, dθ\)\(u=\cos θ\)Dejé.Así,\(du=−\sin θ \, dθ.\)

\(=∫ (u^4−u^2)\,du\)

\(=\dfrac{1}{5}u^5−\dfrac{1}{3}u^3+C\)Sustituto\(\cos θ=u.\)

\(=\dfrac{1}{5}\cos^5θ−\dfrac{1}{3}\cos^3θ+C\)Usa un triángulo de referencia para ver eso\(\cos θ=\sqrt{1−x^2}.\)

\(=\dfrac{1}{5}(1−x^2)^{5/2}−\dfrac{1}{3}(1−x^2)^{3/2}+C.\)

Ejercicio\(\PageIndex{1}\)

Reescribir la integral\(\displaystyle ∫\dfrac{x^3}{\sqrt{25−x^2}}\,dx\) usando la sustitución trigonométrica apropiada (no evaluar la integral).

Pista: Sustituto\(x=5\sin θ\) y\(dx=5\cos θ \, dθ.\)

Responder: \(\displaystyle ∫ 125\sin^3θ \, dθ\)

Integración de expresiones que involucran\(\sqrt{a^2+x^2}\)

Para integrales que contengan\(\sqrt{a^2+x^2}\), primero consideremos el dominio de esta expresión. Ya que\(\sqrt{a^2+x^2}\) se define para todos los valores reales de\(x\), restringimos nuestra elección a aquellas funciones trigonométricas que tienen un rango de todos los números reales. Por lo tanto, nuestra elección se limita a seleccionar cualquiera\(x=a\tan θ\) o\(x=a\cot θ\). Cualquiera de estas sustituciones funcionaría realmente, pero la sustitución estándar es\(x=a\tan θ\) o, de manera equivalente,\(\tan θ=x/a\). Con esta sustitución, hacemos el supuesto de que\(−(π/2)<θ<π/2\), para que también tengamos\(θ=\tan^{−1}(x/a).\) El procedimiento para utilizar esta sustitución se esboza en la siguiente estrategia de resolución de problemas.

Estrategia de resolución de problemas: integración de expresiones que involucran\(\sqrt{a^2+x^2}\)

Verifique si la integral puede ser evaluada fácilmente usando otro método. En algunos casos, es más conveniente utilizar un método alternativo.
Sustituto\(x=a\tan θ\) y\(dx=a\sec^2θ \, dθ.\) Esta sustitución rinde\(\sqrt{a^2+x^2}=\sqrt{a^2+(a\tan θ)^2}=\sqrt{a^2(1+\tan^2θ)}=\sqrt{a^2sec^2θ}=|a\sec θ|=a\sec θ.\) (Desde\(−\dfrac{π}{2}<θ<\dfrac{π}{2}\) y\(\sec θ>0\) sobre este intervalo,\(|a\sec θ|=a\sec θ\).)
Simplifica la expresión.
Evaluar la integral utilizando técnicas de la sección sobre integrales trigonométricas.
Utilice el triángulo de referencia de la Figura\(\PageIndex{4}\) para reescribir el resultado en términos de\(x\). También es posible que necesites usar algunas identidades trigonométricas y la relación\(θ=\tan^{−1}\left(\dfrac{x}{a}\right)\). (Nota: El triángulo de referencia se basa en el supuesto de que\(x>0\); sin embargo, las relaciones trigonométricas producidas a partir del triángulo de referencia son las mismas que las relaciones para las cuales\(x≤0\).)

Ejemplo\(\PageIndex{4}\): Integrating an Expression Involving \(\sqrt{a^2+x^2}\)

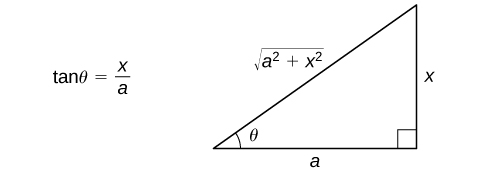
Evaluar\(\displaystyle ∫\dfrac{dx}{\sqrt{1+x^2}}\) y verificar la solución diferenciando.

Solución

Empezar con la sustitución\(x=\tan θ\) y\(dx=sec^2θ\,dθ\). Ya que\(\tan θ=x\), dibuje el triángulo de referencia en la Figura\(\PageIndex{5}\).

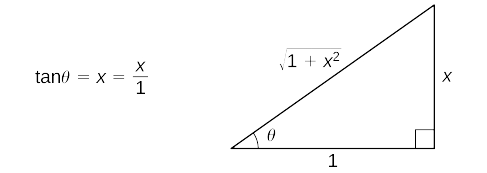
Así,

\ (\ displaystyle\ begin {align*} ∫\ dfrac {dx} {\ sqrt {1+x^2}} &=∫\ dfrac {\ seg^2θ} {\ seg θ} dθ & &\ text {Sustituto} x=\ tan θ\ texto {y} dx=\ seg^2θ\, dθ.\\ [4pt]
& &\ texto {Esta sustitución hace}\ sqrt {1+x^2} =\ seg θ. \ text {Simplificar.}\\ [4pt]
&=∫\ sec θ\, dθ & &\ text {Evalúa la integral.}\\ [4pt]
&=\ ln |\ sec θ+\ tan θ|+C & &\ text {Usa el triángulo de referencia para expresar el resultado en términos de} x.\\ [4pt]
&=\ ln |\ sqrt {1+x^2} +xx|+C\ final {alinear*}\)

Para verificar la solución, diferencie:

\(\dfrac{d}{dx}\Big( \ln |\sqrt{1+x^2}+x|\Big)=\dfrac{1}{\sqrt{1+x^2}+x}⋅\left(\dfrac{x}{\sqrt{1+x^2}}+1\right) =\dfrac{1}{\sqrt{1+x^2}+x}⋅\dfrac{x+\sqrt{1+x^2}}{\sqrt{1+x^2}}=\dfrac{1}{\sqrt{1+x^2}}.\)

Ya que\(\sqrt{1+x^2}+x>0\) para todos los valores de\(x\), podríamos reescribir\( \ln |\sqrt{1+x^2}+x|+C= \ln (\sqrt{1+x^2}+x)+C\), si se desea.

Ejemplo\(\PageIndex{5}\): Evaluating \(∫\dfrac{dx}{\sqrt{1+x^2}}\) Using a Different Substitution

Utilice la sustitución\(x=\sinh θ\) para evaluar\(\displaystyle ∫\dfrac{dx}{\sqrt{1+x^2}}.\)

Solución

Porque\(\sinh θ\) tiene un rango de todos los números reales, y\(1+\sinh^2θ=\cosh^2θ\), también podemos usar la sustitución\(x=\sinh θ\) para evaluar esta integral. En este caso,\(dx=\cosh θ \,dθ.\) Consecuentemente,

\ (\ displaystyle\ begin {alinear*} ∫\ dfrac {dx} {\ sqrt {1+x^2}} &=∫\ dfrac {\ cosh θ} {\ sqrt {1+\ sinh^2θ}} dθ &\ texto {Sustituto} x=\ sinh θ\ texto {y} dx=\ cosh θ\, dθ.\\ [4pt]
& & &\ text {Sustituto} 1+\ sinh^2θ=\ cosh^2θ.\\ [4pt]
&=∫\ dfrac {\ cosh θ} {\ sqrt {\ cosh^2θ}} dθ & amp; &\ text {Desde}\ sqrt {\ cosh^2θ} =|\ cosh θ|\\ [4pt]
&=∫\ dfrac {\ cosh θ} {|\ cosh θ|} dθ & & |\ cosh θ|=\ cosh θ\ text {since}\ cosh θ>0\ text {para todos} θ.\\ [4pt]
=∫\ dfrac {\ cosh θ} {\ cosh θ} dθ & &\ text {Simplificar.}\\ [4pt]
&=∫ 1\, dθ & & \ text {Evalúa la integral.}\\ [4pt]
&=θ+C & &\ text {Desde} x=\ sinh θ,\ text {sabemos} θ=\ sinh^ {−1} x.\\ [4pt]
&=\ sinh^ {−1} x+C.\ end {align*}\)

Análisis

Esta respuesta se ve bastante diferente de la respuesta obtenida usando la sustitución\(x=\tan θ.\) Para ver que las soluciones son las mismas, establecer\(y=\sinh^{−1}x\). Así,\(\sinh y=x.\) a partir de esta ecuación obtenemos:

\[\dfrac{e^y−e^{−y}}{2}=x. \nonumber \]

Después de multiplicar ambos lados por\(2e^y\) y reescribir, esta ecuación se convierte en:

\[e^{2y}−2xe^y−1=0. \nonumber \]

Utilice la ecuación cuadrática para resolver\(e^y\):

\[e^y=\dfrac{2x±\sqrt{4x^2+4}}{2}. \nonumber \]

Simplificando, tenemos:

\[e^y=x±\sqrt{x^2+1}. \nonumber \]

Ya que\(x−\sqrt{x^2+1}<0\), debe ser el caso que\(e^y=x+\sqrt{x^2+1}\). Así,

\[y= \ln (x+\sqrt{x^2+1}). \nonumber \]

Por último, obtenemos

\[\sinh^{−1}x= \ln (x+\sqrt{x^2+1}). \nonumber \]

Después hacemos la observación final de que, desde\(x+\sqrt{x^2+1}>0,\)

\[ \ln (x+\sqrt{x^2+1})= \ln ∣\sqrt{1+x^2}+x∣, \nonumber \]

vemos que los dos métodos diferentes produjeron soluciones equivalentes.

Ejemplo\(\PageIndex{6}\): Finding an Arc Length

Encuentra la longitud de la curva\(y=x^2\) a lo largo del intervalo\([0,\dfrac{1}{2}]\).

Solución

Porque\(\dfrac{dy}{dx}=2x\), la longitud del arco viene dada por

\[∫^{1/2}_0\sqrt{1+(2x)^2}dx=∫^{1/2}_0\sqrt{1+4x^2}dx. \nonumber \]

Para evaluar esta integral, utilice la sustitución\(x=\dfrac{1}{2}\tan θ\) y\(dx=\tfrac{1}{2}\sec^2θ \, dθ\). También necesitamos cambiar los límites de la integración. Si\(x=0\), entonces\(θ=0\) y si\(x=\dfrac{1}{2}\), entonces\(θ=\dfrac{π}{4}.\) Así,

\(∫^{1/2}_0\sqrt{1+4x^2}dx=∫^{π/4}_0\sqrt{1+\tan^2θ}\cdot \tfrac{1}{2}\sec^2θ \, dθ\)Después de la sustitución,\(\sqrt{1+4x^2}=\sec θ\). (Sustituir\(1+\tan^2θ=\sec^2θ\) y simplificar.)

\(=\tfrac{1}{2}∫^{π/4}_0\sec^3θ \, dθ\)Derivamos esta integral en el apartado anterior.

\(=\tfrac{1}{2}(\dfrac{1}{2}\sec θ\tan θ+ \dfrac{1}{2}\ln |\sec θ+\tan θ|)∣^{π/4}_0\)Evaluar y simplificar.

\(=\tfrac{1}{4}(\sqrt{2}+ \ln (\sqrt{2}+1)).\)

Ejercicio\(\PageIndex{2}\)

Reescribir\(\displaystyle ∫ x^3\sqrt{x^2+4}dx\) mediante el uso de una sustitución que implica\(\tan θ\).

Pista: Uso\(x=2\tan θ\) y\(dx=2\sec^2θ \, dθ.\)

Responder: \[ ∫ 32\tan^3θ\sec^3θ \, dθ \nonumber \]

Integración de expresiones que involucran\(\sqrt{x^2−a^2}\)

El dominio de la expresión\(\sqrt{x^2−a^2}\) es\((−∞,−a]∪[a,+∞)\). Así, ya sea\(x\le −a\) o\(x\ge a.\) Por lo tanto,\(\dfrac{x}{a}≤−1\) o\(\dfrac{x}{a}≥1\). Dado que estos intervalos corresponden al rango de\(\sec θ\) en el conjunto\([0,\dfrac{π}{2})∪(\dfrac{π}{2},π]\), tiene sentido usar la sustitución\(\sec θ=\dfrac{x}{a}\) o, equivalentemente,\(x=a\sec θ\), dónde\(0≤θ<\dfrac{π}{2}\) o\(\dfrac{π}{2}<θ≤π\). La sustitución correspondiente para\(dx\) es\(dx=a\sec θ\tan θ \, dθ\). El procedimiento para usar esta sustitución se describe en la siguiente estrategia de resolución de problemas.

Estrategia de resolución de problemas: Integrales que involucran\(\sqrt{x^2−a^2}\)

Verifique si la integral no puede ser evaluada usando otro método. Si es así, tal vez deseemos considerar la posibilidad de aplicar una técnica alternativa.
Sustituto\(x=a\sec θ\) y\(dx=a\sec θ\tan θ \, dθ\). Esta sustitución rinde\[ \sqrt{x^2−a^2}=\sqrt{(a\sec θ)^2−a^2}=\sqrt{a^2(\sec^2θ-1)}=\sqrt{a^2\tan^2θ}=|a\tan θ|. \nonumber \] Para\(x≥a, |a\tan θ|=a\tan θ\) y para\(x≤−a, |a\tan θ|=−a\tan θ.\)
Simplifica la expresión.
Evaluar la integral utilizando técnicas de la sección sobre integrales trigonométricas.
Utilice los triángulos de referencia de la Figura\(\PageIndex{6}\) para reescribir el resultado en términos de\(x\).
También es posible que necesites usar algunas identidades trigonométricas y la relación\(θ=\sec^{−1}\left(\dfrac{x}{a}\right)\). (Nota: Necesitamos ambos triángulos de referencia, ya que los valores de algunas de las relaciones trigonométricas son diferentes dependiendo de si\(x>a\) o\(x<−a\).)

Esta figura tiene dos triángulos rectos. El primer triángulo está en el primer cuadrante del sistema de coordenadas xy y tiene un ángulo etiquetado theta. Este ángulo es opuesto al lado vertical. La hipotenusa está etiquetada x, la pata vertical se etiqueta como la raíz cuadrada de (x^2-a^2), y la pata horizontal está etiquetada como a. la pata horizontal está en el eje x. A la izquierda del triángulo está la ecuación sec (theta) = x/a, x — Figura\(\PageIndex{6}\): Utilizar el triángulo de referencia apropiado para expresar las funciones trigonométricas evaluadas\(θ\) en términos de\(x\).

Ejemplo\(\PageIndex{7}\): Finding the Area of a Region

Encuentra el área de la región entre la gráfica\(f(x)=\sqrt{x^2−9}\) y el eje x en el intervalo\([3,5].\)

Solución

Primero, esboce una gráfica aproximada de la región descrita en el problema, como se muestra en la siguiente figura.

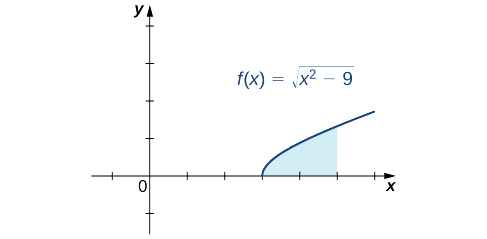
Esta figura es la gráfica de la función f (x) = la raíz cuadrada de (x^2-9). Se trata de una curva creciente que inicia en el eje x a las 3 y se encuentra en el primer cuadrante. Bajo la curva por encima del eje x hay una región sombreada delimitada a la derecha en x = 5. — Figura\(\PageIndex{7}\): Calcular el área de la región sombreada requiere evaluar una integral con una sustitución trigonométrica.

Podemos ver que la zona es\(A=∫^5_3\sqrt{x^2−9}dx\). Evaluar esta integral definida, sustituta\(x=3\sec θ\) y\(dx=3\sec θ\tan θ \, dθ\). También debemos cambiar los límites de la integración. Si\(x=3\), entonces\(3=3\sec θ\) y por lo tanto\(θ=0\). Si\(x=5\), entonces\(θ=\sec^{−1}(\dfrac{5}{3})\). Después de hacer estas sustituciones y simplificar, tenemos

Área\(=∫^5_3\sqrt{x^2−9}dx\)

\(=∫^{\sec^{−1}(5/3)}_09\tan^2θ\sec θ \, dθ\)Uso\(\tan^2θ=\sec^2θ - 1.\)

\(=∫^{\sec^{−1}(5/3)}_09(\sec^2θ−1)\sec θ \, dθ\)Ampliar.

\(=∫^{\sec^{−1}(5/3)}_09(\sec^3θ−\sec θ)\,dθ\)Evaluar la integral.

\(=(\dfrac{9}{2} \ln |\sec θ+\tan θ|+\dfrac{9}{2}\sec θ\tan θ)−9 \ln |\sec θ+\tan θ|∣^{\sec^{−1}(5/3)}_0\)Simplificar.

\(=\dfrac{9}{2}\sec θ\tan θ−\dfrac{9}{2} \ln |\sec θ+\tan θ|∣^{\sec^{−1}(5/3)}_0\)Evaluar. Uso\(\sec(\sec^{−1}\dfrac{5}{3})=\dfrac{5}{3}\) y\(\tan(\sec^{−1}\dfrac{5}{3})=\dfrac{4}{3}.\)

\(=\dfrac{9}{2}⋅\dfrac{5}{3}⋅\dfrac{4}{3}−\dfrac{9}{2} \ln ∣\dfrac{5}{3}+\dfrac{4}{3}∣−(\dfrac{9}{2}⋅1⋅0−\dfrac{9}{2} \ln |1+0|)\)

\(=10−\dfrac{9}{2} \ln 3\)

Ejercicio\(\PageIndex{3}\)

Evaluar\[∫\dfrac{dx}{\sqrt{x^2−4}}. \nonumber \] Supongamos que\(x>2.\)

Pista: Sustituto\(x=2\sec θ\) y\(dx=2\sec θ\tan θ \, dθ.\)

Responder: \[ \ln |\dfrac{x}{2}+\dfrac{\sqrt{x^2−4}}{2}|+C \nonumber \]

Conceptos clave

Para integrales que involucren\(\sqrt{a^2−x^2}\), use la sustitución\(x=a\sin θ\) y\(dx=a\cos θ \, dθ.\)
Para integrales que involucren\(\sqrt{a^2+x^2}\), use la sustitución\(x=a\tan θ\) y\(dx=a\sec^2θ \, dθ\).
Para integrales que involucren\(\sqrt{x^2−a^2}\), sustituyan\(x=a\sec θ\) y\(dx=a\sec θ\tan θ \,dθ\).

Glosario

sustitución trigonométrica: una técnica de integración que convierte una integral algebraica que contiene expresiones de la forma\(\sqrt{a^2−x^2}\)\(\sqrt{a^2+x^2}\), o\(\sqrt{x^2−a^2}\) en una integral trigonométrica