7.6: Integración numérica
- Page ID
- 116387
- Aproximar el valor de una integral definida utilizando las reglas de punto medio y trapezoidales.
- Determinar el error absoluto y relativo en el uso de una técnica de integración numérica.
- Estime el error absoluto y relativo usando una fórmula ligada a errores.
- Reconocer cuándo el punto medio y el trapezoidal gobiernan o subestiman el verdadero valor de una integral.
- Utilice la regla de Simpson para aproximar el valor de una integral definida a una precisión dada.
Los antiderivados de muchas funciones no pueden expresarse o no pueden expresarse fácilmente en forma cerrada (es decir, en términos de funciones conocidas). En consecuencia, en lugar de evaluar directamente integrales definidas de estas funciones, recurrimos a diversas técnicas de integración numérica para aproximar sus valores. En esta sección, exploramos varias de estas técnicas. Además, se examina el proceso de estimación del error en el uso de estas técnicas.
La regla del punto medio
Anteriormente en este texto definimos la integral definida de una función sobre un intervalo como el límite de las sumas de Riemann. En general, cualquier suma de Riemann de una función\( f(x)\) a lo largo de un intervalo\([a,b]\) puede verse como una estimación de\(\displaystyle ∫^b_af(x)\,dx\). Recordemos que una suma de Riemann de una función\( f(x)\) sobre un intervalo\( [a,b]\) se obtiene seleccionando una partición
\[ P=\{x_0,x_1,x_2,…,x_n\} \nonumber \]
donde\(\quad a=x_0<x_1<x_2<⋯<x_n=b \)
y un conjunto
\[ S=\{x^*_1,x^*_2,…,x^*_n\} \nonumber \]
donde\(x_{i−1}≤x^*_i≤x_i \quad \text{for all} \, i.\)
La suma de Riemann correspondiente a la partición\(P\) y al conjunto\(S\) viene dada por\(\displaystyle \sum^n_{i=1}f(x^*_i)Δx_i\), donde\( Δx_i=x_i−x_{i−1},\) la longitud del\( i^{\text{th}}\) subintervalo.
La regla de punto medio para estimar una integral definida utiliza una suma de Riemann con subintervalos de igual ancho y los puntos medios,\( m_i\), de cada subintervalo en lugar de\( x^*_i\). Formalmente, declaramos un teorema respecto a la convergencia de la regla del punto medio de la siguiente manera.
Supongamos que\( f(x)\) es continuo en\([a,b]\). Dejar\( n\) ser un entero positivo y\( Δx=\dfrac{b−a}{n}\). Si\( [a,b]\) se divide en\( n\) subintervalos, cada uno de longitud\( Δx\), y\( m_i\) es el punto medio del\( i^{\text{th}}\) subintervalo, establecer
\[M_n=\sum_{i=1}^nf(m_i)Δx. \nonumber \]
Entonces\(\displaystyle \lim_{n→∞}M_n=∫^b_af(x)\,dx.\)
Como podemos ver en la Figura\(\PageIndex{1}\), si se\( f(x)≥0\) termina\( [a,b]\), entonces\(\displaystyle \sum^n_{i=1}f(m_i)Δx\) corresponde a la suma de las áreas de rectángulos aproximándose al área entre la gráfica de\( f(x)\) y el\(x\) eje -sobre\([a,b]\). La gráfica muestra los rectángulos\(M_4\) correspondientes a una función no negativa en un intervalo cerrado\([a,b].\)
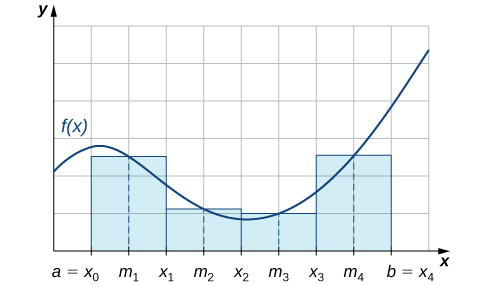
Utilice la regla de punto medio para estimar\(\displaystyle ∫^1_0x^2\,dx\) usando cuatro subintervalos. Comparar el resultado con el valor real de esta integral.
Solución: Cada subintervalo tiene longitud\( Δx=\dfrac{1−0}{4}=\dfrac{1}{4}.\) Por lo tanto, los subintervalos consisten en
\[\left[0,\tfrac{1}{4}\right],\,\left[\tfrac{1}{4},\tfrac{1}{2}\right],\,\left[\tfrac{1}{2},\tfrac{3}{4}\right],\, \text{and}\, \left[\tfrac{3}{4},1\right].\nonumber \]
Los puntos medios de estos subintervalos son\(\left\{\frac{1}{8},\,\frac{3}{8},\,\frac{5}{8},\, \frac{7}{8}\right\}.\) Así,
\[\begin{align*} M_4 &=\frac{1}{4}\cdot f\left(\frac{1}{8}\right)+\frac{1}{4}\cdot f\left(\frac{3}{8}\right)+\frac{1}{4}\cdot f\left(\frac{5}{8}\right)+\frac{1}{4}\cdot f\left(\frac{7}{8}\right) \\[4pt] &=\frac{1}{4}⋅\frac{1}{64}+\frac{1}{4}⋅\frac{9}{64}+\frac{1}{4}⋅\frac{25}{64}+\frac{1}{4}⋅\frac{49}{64}\\[4pt] &=\frac{21}{64} = 0.328125. \end{align*}\]
Desde
\[ ∫^1_0x^2\,dx=\frac{1}{3},\nonumber \]
el error absoluto en esta aproximación es:
\[\left\lvert\dfrac{1}{3}−\dfrac{21}{64}\right\rvert=\dfrac{1}{192}≈0.0052, \nonumber \]
y vemos que la regla del punto medio produce una estimación que es algo cercana al valor real de la integral definida.
Se utiliza\(M_6\) para estimar la longitud de la curva\(y=\frac{1}{2}x^2\) en\([1,4]\).
Solución: La longitud de\(y=\frac{1}{2}x^2\) on\([1,4]\) es
\[s = ∫^4_1\sqrt{1+\left(\frac{dy}{dx}\right)^2}\,dx.\nonumber \]
Ya que\(\dfrac{dy}{dx}=x\), esta integral se convierte\(\displaystyle ∫^4_1\sqrt{1+x^2}\,dx.\)
Si\([1,4]\) se divide en seis subintervalos, entonces cada subintervalo tiene longitud\(Δx=\dfrac{4−1}{6}=\dfrac{1}{2}\) y los puntos medios de los subintervalos son\(\left\{\frac{5}{4},\frac{7}{4},\frac{9}{4},\frac{11}{4},\frac{13}{4},\frac{15}{4}\right\}\). Si establecemos\(f(x)=\sqrt{1+x^2}\),
\[\begin{align*} M_6 &=\tfrac{1}{2}\cdot f\left(\frac{5}{4}\right)+\tfrac{1}{2}\cdot f\left(\frac{7}{4}\right)+\frac{1}{2}\cdot f\left(\frac{9}{4}\right)+\frac{1}{2}\cdot f\left(\frac{11}{4}\right)+\frac{1}{2}\cdot f\left(\frac{13}{4}\right)+\frac{1}{2}\cdot f\left(\frac{15}{4}\right) \\[4pt] &≈\frac{1}{2}(1.6008+2.0156+2.4622+2.9262+3.4004+3.8810)=8.1431 \, \text{ units}. \end{align*}\]
Usar la regla de punto medio con\( n=2\) para estimar\(\displaystyle ∫^2_1\frac{1}{x}\,dx.\)
- Pista
-
\( Δx=\frac{1}{2}, \quad m_1=\frac{5}{4},\quad \text{and} \quad m_2=\frac{7}{4}.\)
- Contestar
-
\(\dfrac{24}{35}\approx 0.685714\)
La Regla Trapezoidal
También podemos aproximar el valor de una integral definida usando trapecios en lugar de rectángulos. En la Figura\(\PageIndex{2}\), el área debajo de la curva es aproximada por trapecios en lugar de por rectángulos.
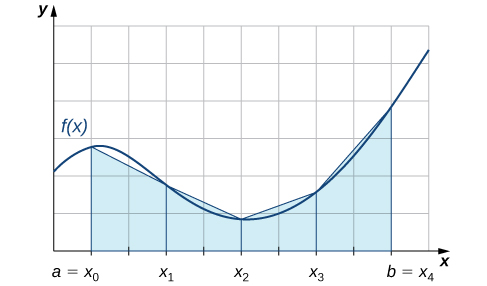
La regla trapezoidal para estimar integrales definidas utiliza trapezoides en lugar de rectángulos para aproximar el área bajo una curva. Para conocer la forma final de la regla, considere los trapecios mostrados en la Figura\(\PageIndex{2}\). Suponemos que la longitud de cada subintervalo viene dada por\(Δx\). En primer lugar, recordemos que el área de un trapecio con una altura de\(h\) y bases de longitud\(b_1\) y\(b_2\) está dada por\(\text{Area}=\frac{1}{2}h(b_1+b_2)\). Vemos que el primer trapecio tiene una altura\(Δx\) y bases paralelas de longitud\( f(x_0)\) y\( f(x_1)\). Así, el área del primer trapecio en la Figura\(\PageIndex{2}\) es
\[ \frac{1}{2}Δx\Big(f(x_0)+f(x_1)\Big).\nonumber \]
Las áreas de los tres trapecios restantes son
\(\dfrac{1}{2}Δx\Big(f(x_1)+f(x_2)\Big),\, \dfrac{1}{2}Δx\Big(f(x_2)+f(x_3)\Big),\)y\( \dfrac{1}{2}Δx\Big(f(x_3)+f(x_4)\Big).\)
En consecuencia,
\[∫^b_af(x)\,dx≈\frac{1}{2}Δx\Big(f(x_0)+f(x_1)\Big)+\frac{1}{2}Δx\Big(f(x_1)+f(x_2)\Big)+\frac{1}{2}Δx\Big(f(x_2)+f(x_3)\Big)+\frac{1}{2}Δx\Big(f(x_3)+f(x_4)\Big).\nonumber \]
Después de sacar un factor común de\(\frac{1}{2}Δx\) y combinar términos similares, tenemos
\[ ∫^b_af(x)\,dx≈\frac{Δx}{2}\Big[f(x_0)+2\,f(x_1)+2\,f(x_2)+2\,f(x_3)+f(x_4)\Big].\nonumber \]
Generalizando, declaramos formalmente la siguiente regla.
Supongamos que\(f(x)\) es continuo sobre\([a,b]\). Dejar\(n\) ser un entero positivo y\(Δx=\dfrac{b−a}{n}\). \( [a,b]\)Se dividen en\(n\) subintervalos, cada uno de longitud\(Δx\), con puntos finales en\( P=\{x_0,x_1,x_2…,x_n\}.\)
Set
\[T_n=\frac{Δx}{2}\Big[f(x_0)+2\, f(x_1)+2\, f(x_2)+⋯+2\, f(x_{n−1})+f(x_n)\Big]. \nonumber \]
Entonces,\(\displaystyle \lim_{n→+∞}T_n=∫^b_af(x)\,dx.\)
Antes de continuar, hagamos algunas observaciones sobre la regla trapezoidal. En primer lugar, es útil señalar que
\(T_n=\dfrac{1}{2}(L_n+R_n)\)dónde\(\displaystyle L_n=\sum_{i=1}^nf(x_{i−1})Δx\) y\(\displaystyle R_n=\sum_{i=1}^nf(x_i)Δx.\)
Es decir,\(L_n\) y\(R_n\) aproximar la integral usando los extremos izquierdo y derecho de cada subintervalo, respectivamente. Además, un cuidadoso examen de la Figura nos\(\PageIndex{3}\) lleva a hacer las siguientes observaciones sobre el uso de las reglas trapezoidales y reglas de punto medio para estimar la integral definida de una función no negativa. La regla trapezoidal tiende a sobreestimar el valor de una integral definida sistemáticamente a lo largo de intervalos donde la función es cóncava hacia arriba y a subestimar sistemáticamente el valor de una integral definida a lo largo de intervalos donde la función es cóncava hacia abajo. Por otro lado, la regla del punto medio tiende a promediar un poco estos errores sobreestimando parcialmente y subestimando parcialmente el valor de la integral definida sobre estos mismos tipos de intervalos. Esto nos lleva a plantear la hipótesis de que, en general, la regla del punto medio tiende a ser más precisa que la regla trapezoidal.
Utilice la regla trapezoidal para estimar\(\displaystyle ∫^1_0x^2\,dx\) usando cuatro subintervalos.
Solución
Los puntos finales de los subintervalos constan de elementos del conjunto\(P=\left\{0,\frac{1}{4},\, \frac{1}{2},\, \frac{3}{4},1\right\}\) y\(Δx=\frac{1−0}{4}=\frac{1}{4}.\) Así,
\ [\ begin {align*} ^1_0x^2dx &≈\ frac {1} {2} ⋅\ frac {1} {4}\ Grande [f (0) +2\, f\ izquierda (\ tfrac {1} {4}\ derecha) +2\, f\ izquierda (\ tfrac {1} {2}\ derecha) +2\, f\ izquierda (\ tfrac {3} {4}\ derecha) +f (1)\ Grande]\\ [4pt]
&=\ tfrac {1} {8}\ grande (0+2⋅\ tfrac {1} {16} +2⋅\ tfrac {1} {4} +2⋅\ tfrac {9} {16} +1\ grande)\\[4pt] &=\frac{11}{32} = 0.34375\end{align*}\]
Utilice la regla trapezoidal con\( n=2\) para estimar\(\displaystyle ∫^2_1\frac{1}{x}\,dx.\)
- Pista
-
Set\(Δx=\dfrac{1}{2}.\) Los puntos finales de los subintervalos son los elementos del conjunto\(P=\left\{1,\frac{3}{2},2\right\}.\)
- Contestar
-
\(\dfrac{17}{24} \approx 0.708333\)
Error absoluto y relativo
Un aspecto importante del uso de estas reglas de aproximación numérica consiste en calcular el error al usarlas para estimar el valor de una integral definida. Primero necesitamos definir el error absoluto y el error relativo.
Si\(B\) es nuestra estimación de alguna cantidad que tiene un valor real de\(A\), entonces el error absoluto viene dado por\(|A−B|\).
El error relativo es el error como porcentaje del valor real y viene dado por\[\left\lvert\frac{A−B}{A}\right\rvert⋅100\%. \nonumber \]
Calcular el error absoluto y relativo en la estimación de\(\displaystyle ∫^1_0x^2\,dx\) usar la regla de punto medio, que se encuentra en Ejemplo\(\PageIndex{1}\).
Solución: El valor calculado es\(\displaystyle ∫^1_0x^2\,dx=\frac{1}{3}\) y nuestra estimación del ejemplo es\(M_4=\frac{21}{64}\). Así, el error absoluto viene dado por\(\left\lvert\frac{1}{3}−\frac{21}{64}\right\rvert=\frac{1}{192}≈0.0052.\)
El error relativo es\[\frac{1/192}{1/3}=\frac{1}{64}≈0.015625≈1.6\%.\nonumber \]
Calcular el error absoluto y relativo en la estimación de\(\displaystyle ∫^1_0x^2\,dx\) usar la regla trapezoidal, que se encuentra en Ejemplo\(\PageIndex{3}\).
Solución: El valor calculado es\(\displaystyle ∫^1_0x^2\,dx=\frac{1}{3}\) y nuestra estimación del ejemplo es\(T_4=\frac{11}{32}\). Así, el error absoluto viene dado por\(\left\lvert\frac{1}{3}−\frac{11}{32}\right\rvert=\frac{1}{96}≈0.0104.\)
El error relativo viene dado por\[\frac{1/96}{1/3}=0.03125≈3.1\%.\nonumber \]
En un punto de control anterior, estimamos\(\displaystyle ∫^2_1\frac{1}{x}\,dx\) que estamos\(\frac{24}{35}\) usando\(M_2\). El valor real de esta integral es\(\ln 2\). Usar\(\frac{24}{35}≈0.6857\) y\(\ln 2≈0.6931,\) calcular el error absoluto y el error relativo.
- Pista
-
Usa los ejemplos anteriores como guía.
- Contestar
-
error absoluto\(\approx 0.0074,\) y error relativo\(\approx 1.1\%\)
límites de error en el punto medio y las reglas trapezoidales
En los dos ejemplos anteriores, pudimos comparar nuestra estimación de una integral con el valor real de la integral; sin embargo, normalmente no tenemos este lujo. En general, si estamos aproximando a una integral, lo estamos haciendo porque no podemos calcular fácilmente el valor exacto de la propia integral. Por lo tanto, a menudo es útil poder determinar un límite superior para el error en una aproximación de una integral. El siguiente teorema proporciona límites de error para las reglas de punto medio y trapezoidales. El teorema se afirma sin pruebas.
Dejar\(f(x)\) ser una función continua sobre\([a,b]\), teniendo una segunda derivada a\(f''(x)\) lo largo de este intervalo. Si\(M\) es el valor máximo de\(|f''(x)|\) over\([a,b]\), entonces los límites superiores para el error\(T_n\) al usar\(M_n\) y estimar\(\displaystyle ∫^b_af(x)\,dx\) son
\[\text{Error in}\, M_n≤\frac{M(b−a)^3}{24n^2}\label{MidError} \]
y
\[\text{Error in}\, T_n≤\frac{M(b−a)^3}{12n^2} \nonumber \].
Podemos usar estos límites para determinar el valor de\(n\) necesario para garantizar que el error en una estimación sea menor que un valor especificado.
¿Qué valor de se\(n\) debe utilizar para garantizar que una estimación de\(\displaystyle ∫^1_0e^{x^2}\,dx\) es exacta a dentro\(0.01\) si utilizamos la regla del punto medio?
Solución
Comenzamos por determinar el valor de\(M\), el valor máximo de\( |f''(x)|\) más\( [0,1]\) para\( f(x)=e^{x^2}\). Ya\( f′(x)=2xe^{x^2},\) que tenemos
\[ f''(x)=2e^{x^2}+4x^2e^{x^2}.\nonumber \]
Por lo tanto,
\[ |f''(x)|=2e^{x^2}(1+2x^2)≤2⋅e⋅3=6e.\nonumber \]
A partir de la ecuación ligada a errores\(\ref{MidError}\), tenemos
\[ \text{Error in}\, M_n≤\frac{M(b−a)^3}{24n^2}≤\frac{6e(1−0)^3}{24n^2}=\frac{6e}{24n^2}.\nonumber \]
Ahora resolvemos la siguiente desigualdad para\(n\):
\[\frac{6e}{24n^2}≤0.01.\nonumber \]
Así,\(n≥\sqrt{\frac{600e}{24}}≈8.24.\) ya que\(n\) debe ser un entero que satisfaga esta desigualdad, una elección de\(n=9\) garantizaría que
\[ \left\lvert ∫^1_0e^{x^2}\,dx−M_n \right\rvert <0.01.\nonumber \]
Análisis
Podríamos haber tenido la tentación de redondear\(8.24\) hacia abajo y elegir\(n=8\), pero esto sería incorrecto porque debemos tener un número entero mayor o igual a\(8.24\). Debemos tener en cuenta que las estimaciones de error proporcionan un límite superior solo para el error. La estimación real puede, de hecho, ser una aproximación mucho mejor que la que indica el límite de error.
Use la ecuación\(\ref{MidError}\) para encontrar un límite superior para el error\(M_4\) al usar para estimar\(\displaystyle ∫^1_0x^2\,dx.\)
- Pista
-
\(f''(x)=2,\)por lo\(M=2.\)
- Contestar
-
\(\dfrac{1}{192}\)
Regla de Simpson
Con la regla de punto medio, estimamos áreas de regiones bajo curvas usando rectángulos. En cierto sentido, aproximamos la curva con funciones constantes por partes. Con la regla trapezoidal, aproximamos la curva mediante el uso de funciones lineales por tramos. ¿Y si fuéramos, en cambio, para aproximar una curva usando funciones cuadráticas por tramos? Con la regla de Simpson, hacemos justamente esto. Particionamos el intervalo en un número par de subintervalos, cada uno de igual ancho. Sobre el primer par de subintervalos aproximamos\(\displaystyle ∫^{x_2}_{x_0}f(x)\,dx\) con\(\displaystyle ∫^{x_2}_{x_0}p(x)\,dx\), donde\(p(x)=Ax^2+Bx+C\) está la función cuadrática que pasa a través\((x_0,f(x_0)), \,(x_1,f(x_1)),\) y\((x_2,f(x_2))\) (Figura\(\PageIndex{4}\)). Durante el siguiente par de subintervalos aproximamos\(\displaystyle ∫^{x_4}_{x_2}f(x)\,dx\) con la integral de otra función cuadrática pasando a través\( (x_2,f(x_2)), \,(x_3,f(x_3)),\) y\((x_4,f(x_4)).\) Este proceso se continúa con cada par sucesivo de subintervalos.
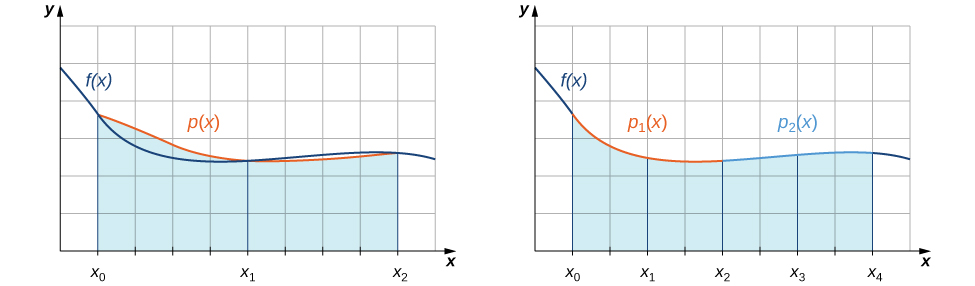
Para entender la fórmula que obtenemos para la regla de Simpson, comenzamos por derivar una fórmula para esta aproximación sobre los dos primeros subintervalos. A medida que avanzamos por la derivación, debemos tener en cuenta las siguientes relaciones:
\[f(x_0)=p(x_0)=Ax_0^2+Bx_0+C \nonumber \]
\[f(x_1)=p(x_1)=Ax_1^2+Bx_1+C \nonumber \]
\[f(x_2)=p(x_2)=Ax_2^2+Bx_2+C \nonumber \]
\(x_2−x_0=2Δx\), donde\(Δx\) es la longitud de un subintervalo.
\(x_2+x_0=2x_1,\)ya que\(x_1=\dfrac{(x_2+x_0)}{2}\).
Por lo tanto,
\ [\ begin {align*} ^ {x_2} _ {x_0} f (x)\, dx &≈^ {x_2} _ {x_0} p (x)\, dx\\ [4pt]
&=^ {x_2} _ {x_0} (Ax^2+Bx+C)\, dx\\ [4pt]
&=\ izquierda (\ frac {A} {3} x^3+\ frac {B} {2} x^2+cx\ derecha)\ big|^ {x_2} _ {x_0} & &\ text {Encuentra la antiderivada.}\\ [4pt]
&=\ frac {A} {3} (x_2^3−x_0^3) +\ frac {B} {2} (x_2^2−x_0^2) +C (x_2−x_0) &\ text {Evalúa la antiderivada.}\\ [4pt]
&=\ frac {A} {3} (x_2−x_0) (x_2^2+x_2x_0+x_0^2) +\ frac {B} {2} (x_2−x_0) (x_2+x_0) +C (x_2−x_0)\\ [4pt]
&=\ frac {x_2−x_0} {6}\ bigg (2A (x_2^2+x_2x_0+x_0^2) +3B (x_2+x_0) +6C\ bigg) & &\ text {Factor out}\,\ frac {x_2−x_0} {6}.\\ [4pt]
&=\ frac {Δx} {3}\ bigg ((Ax_2^2+Bx_2+C) + (Ax_0^2+Bx_0+C) +A (x_2^2+2x_2x_0+x_0^2) +2B (x2+2^x_0) +4C\ bigg) & &\ text {Reorganizar los términos. Nota:}\ enspace Δx =\ frac {x_2−x_0} {2}\\ [4pt]
&=\ frac {Δx} {3}\ big (f (x_2) +f (x_0) +A (x_2+x_0) ^2+2B (x_2+x_0) +4C\ big) &\ text {Factor y sustituto:}\\ [4pt]
& & &\ quad f (x_2) =Ax_2^2+Bx_2+C\ enspace\ texto {y}\ enspace f (x_0) =Ax_0^2+Bx_0+C.\\ [4pt]
&=\ frac {Δx} {3}\ grande (f (x_2) +f (x_0) +A (2x_1) ^2+2B (2x_1) +4C\ grande) &\ texto {Sustituto}\, x_2+x_0=2x_1.\\ [4pt]
& &\ quad\ text {Nota:}\, x_1 =\ frac {x_2+x_0} {2}\ enspace\ text {es el punto medio.}\\ [4pt]
&=\ frac {Δx} {3}\ big (f (x_2) +4f (x_1) +f (x_0)\ big). & &\ text {Expandir y sustituir}\, f (x_1) =Ax_1^2+Bx_1+C.\ end {align*}\]
Si aproximamos\(\displaystyle ∫^{x_4}_{x_2}f(x)\,dx\) usando el mismo método, vemos que tenemos
\[∫^{x_4}_{x_2}f(x)\,dx≈\frac{Δx}{3}(f(x_4)+4\,f(x_3)+f(x_2)).\nonumber \]
Combinando estas dos aproximaciones, obtenemos
\[∫^{x_4}_{x_0}f(x)\,dx≈\frac{Δx}{3}(f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f(x_3)+f(x_4)).\nonumber \]
El patrón continúa a medida que agregamos pares de subintervalos a nuestra aproximación. La regla general podrá manifestarse de la siguiente manera.
Supongamos que\(f(x)\) es continuo sobre\([a,b]\). Dejar\(n\) ser un entero par positivo y\(Δx=\dfrac{b−a}{n}\). Dejar\([a,b]\) dividirse en\(n\) subintervalos, cada uno de longitud\(Δx\), con puntos finales en\(P=\{x_0,x_1,x_2,…,x_n\}.\) Set
\[S_n=\frac{Δx}{3}\Big[f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f(x_3)+2\,f(x_4)+⋯+2\,f(x_{n−2})+4\,f(x_{n−1})+f(x_n)\Big]. \nonumber \]
Entonces,
\[\lim_{n→+∞}S_n=∫^b_af(x)\,dx.\nonumber \]
Así como la regla trapezoidal es el promedio de las reglas izquierda y derecha para estimar integrales definidas, la regla de Simpson se puede obtener a partir de las reglas de punto medio y trapezoidal usando un promedio ponderado. Se puede demostrar que\(S_{2n}=\left(\frac{2}{3}\right)M_n+\left(\frac{1}{3}\right)T_n\).
También es posible poner un límite al error al usar la regla de Simpson para aproximar una integral definida. El límite en el error viene dado por la siguiente regla:
Dejar\(f(x)\) ser una función continua sobre\([a,b]\) tener una cuarta derivada,\( f^{(4)}(x)\), a lo largo de este intervalo. Si\(M\) es el valor máximo de\(∣f^{(4)}(x)∣\) over\([a,b]\), entonces el límite superior para el error\(S_n\) al usar para estimar\(\displaystyle ∫^b_af(x)\,dx\) viene dado por
\[\text{Error in}\, S_n≤\frac{M(b−a)^5}{180n^4}. \nonumber \]
Úselo\(S_2\) para aproximar\(\displaystyle ∫^1_0x^3\,dx\). Estimar un límite para el error en\(S_2\).
Solución
Ya que\([0,1]\) se divide en dos intervalos, cada subintervalo tiene longitud\(Δx=\frac{1−0}{2}=\frac{1}{2}\). Los puntos finales de estos subintervalos son\(\left\{0,\frac{1}{2},1\right\}\). Si establecemos\(f(x)=x^3,\) entonces
\[S_2=\frac{1}{3}⋅\frac{1}{2}(f(0)+4\,f(\frac{1}{2})+f(1))=\frac{1}{6}(0+4⋅\frac{1}{8}+1)=\frac{1}{4}.\nonumber \]
Desde\( f^{(4)}(x)=0\) y consecuentemente\(M=0,\) vemos que
Error en\(S_2≤\frac{0(1)^5}{180⋅2^4}=0.\)
Este límite indica que el valor obtenido a través de la regla de Simpson es exacto. Una comprobación rápida verificará que, de hecho,\(\displaystyle ∫^1_0x^3\,dx=\frac{1}{4}.\)
Se utiliza\(S_6\) para estimar la longitud de la curva\(y=\frac{1}{2}x^2\) sobre\([1,4].\)
Solución
La longitud de\(y=\frac{1}{2}x^2\) más\([1,4]\) es\(\displaystyle ∫^4_1\sqrt{1+x^2}\,dx\). Si\([1,4]\) dividimos en seis subintervalos, entonces cada subintervalo tiene longitud\(Δx=\frac{4−1}{6}=\frac{1}{2}\), y los puntos finales de los subintervalos son\( \left\{1,\frac{3}{2},2,\frac{5}{2},3,\frac{7}{2},4\right\}.\) Setting\( f(x)=\sqrt{1+x^2}\),
\[S_6=\frac{1}{3}⋅\frac{1}{2}(f(1)+4f(\frac{3}{2})+2f(2)+4f(\frac{5}{2})+2f(3)+4f(\frac{7}{2})+f(4)).\nonumber \]
Después de sustituir, tenemos
\[S_6=\frac{1}{6}(1.4142+4⋅1.80278+2⋅2.23607+4⋅2.69258+2⋅3.16228+4⋅3.64005+4.12311)≈8.14594\,\text{units}. \nonumber \]
Utilizar\(S_2\) para estimar\(\displaystyle ∫^2_1\frac{1}{x}\,dx.\)
- Pista
-
\[S_2=\frac{1}{3}Δx\left(f(x_0)+4f(x_1)+f(x_2)\right) \nonumber \]
- Contestar
-
\(\frac{25}{36} \approx 0.694444\)
Conceptos clave
- Podemos utilizar la integración numérica para estimar los valores de integrales definidas cuando una forma cerrada de la integral es difícil de encontrar o cuando se necesita un valor aproximado solo de la integral definida.
- Las técnicas más utilizadas para la integración numérica son la regla del punto medio, la regla trapezoidal y la regla de Simpson.
- La regla de punto medio se aproxima a la integral definida usando regiones rectangulares, mientras que la regla trapezoidal se aproxima a la integral definida usando aproximaciones trapezoidales.
- La regla de Simpson se aproxima a la integral definida aproximando primero la función original usando funciones cuadráticas por tramos.
Ecuaciones Clave
- Regla de punto medio
\(\displaystyle M_n=\sum^n_{i=1}f(m_i)Δx\)
- Regla trapezoidal
\(T_n=\frac{Δx}{2}\Big[f(x_0)+2\,f(x_1)+2\,f(x_2)+⋯+2\,f(x_{n−1})+f(x_n)\Big]\)
- La regla de Simpson
\(S_n=\frac{Δx}{3}\Big[f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f(x_3)+2\,f(x_4)+4\,f(x_5)+⋯+2\,f(x_{n−2})+4\,f(x_{n−1})+f(x_n)\Big]\)
- Error enlazado para regla de punto medio
Error en\(M_n≤\dfrac{M(b−a)^3}{24n^2}\), donde\(M\) es el valor máximo de\(|f''(x)|\) over\([a,b]\).
- Encuadernación de error para regla trapezoidal
Error en\(T_n≤\dfrac{M(b−a)^3}{12n^2}\), donde\(M\) es el valor máximo de\(|f''(x)|\) over\([a,b]\).
- Error vinculado a la regla de Simpson
Error en\(S_n≤\dfrac{M(b−a)^5}{180n^4}\), donde\(M\) es el valor máximo de\(∣f^{(4)}(x)∣\) over\([a,b]\).
Glosario
- error absoluto
- si\(B\) es una estimación de alguna cantidad que tiene un valor real de\(A\), entonces el error absoluto viene dado por\( |A−B|\)
- regla de punto medio
- una regla que usa una suma Riemann de la forma\(\displaystyle M_n=\sum^n_{i=1}f(m_i)Δx\), donde\( m_i\) está el punto medio del\(i^{\text{th}}\) subintervalo para aproximarse\(\displaystyle ∫^b_af(x)\,dx\)
- integración numérica
- la variedad de métodos numéricos utilizados para estimar el valor de una integral definida, incluyendo la regla del punto medio, la regla trapezoidal y la regla de Simpson
- error relativo
- error como porcentaje del valor real, dado por\[\text{relative error}=\left|\frac{A−B}{A}\right|⋅100\%\nonumber \]
- La regla de Simpson
- una regla que se aproxima\(\displaystyle ∫^b_af(x)\,dx\) usando el área bajo una función cuadrática por tramos.
La aproximación\(S_n\) a\(\displaystyle ∫^b_af(x)\,dx\) viene dada por\[S_n=\frac{Δx}{3}\big(f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f(x_3)+2\,f(x_4)+⋯+2\,f(x_{n−2})+4\,f(x_{n−1})+f(x_n)\big).\nonumber \]
- regla trapezoidal
- una regla que se aproxima\(\displaystyle ∫^b_af(x)\,dx\) usando el área de trapecios.
La aproximación\(T_n\) a\(\displaystyle ∫^b_af(x)\,dx\) viene dada por\[T_n=\frac{Δx}{2}\big(f(x_0)+2\, f(x_1)+2\, f(x_2)+⋯+2\, f(x_{n−1})+f(x_n)\big).\nonumber \]
Colaboradores y Atribuciones
- Template:ContribOpenStaxCalc
- Edited by Paul Seeburger (Monroe Community College). Notes added to development of area under a parabola and typos fixed in original text.