7.1: Integración por Partes

Objetivos de aprendizaje

• Reconocer cuándo usar la integración por partes.
• Utilice la fórmula de integración por partes para resolver problemas de integración.
• Utilice la fórmula de integración por partes para integrales definidas.

A estas alturas ya tenemos un procedimiento bastante minucioso sobre cómo evaluar muchas integrales básicas. No obstante, aunque podemos integrarnos$∫x \sin (x^2)\,dx$ usando la sustitución$u=x^2$,, algo tan simple como nos$∫x\sin x\,\,dx$ desafía. Muchos estudiantes quieren saber si existe una regla de producto para la integración. No lo hay, pero hay una técnica basada en la regla del producto para la diferenciación que nos permite intercambiar una integral por otra. A esta técnica la llamamos integración por partes.

La fórmula de integración por partes

Si,$h(x)=f(x)g(x)$, entonces mediante el uso de la regla del producto, obtenemos

$$h′(x)=f′(x)g(x)+g′(x)f(x). \label{eq1}$$

Aunque al principio pueda parecer contraproducente, ahora vamos a integrar ambos lados de la Ecuación\ ref {eq1}:

$$∫h′(x)\,\,dx=∫(g(x)f′(x)+f(x)g′(x))\,\,dx. \nonumber$$

Esto nos da

$$h(x)=f(x)g(x)=∫g(x)f′(x)\,dx+∫f(x)g′(x)\,\,dx. \nonumber$$

Ahora resolvemos para$∫f(x)g′(x)\,\,dx:$

$$∫f(x)g′(x)\,dx=f(x)g(x)−∫g(x)f′(x)\,\,dx. \nonumber$$

Al hacer las sustituciones$u=f(x)$ y$v=g(x)$, que a su vez hacen$du=f′(x)\,dx$ y$dv=g′(x)\,dx$, tenemos la forma más compacta

$$∫u\,dv=uv−∫v\,du. \nonumber$$

Integración por Partes

Dejar$u=f(x)$ y$v=g(x)$ ser funciones con derivadas continuas. Entonces, la fórmula de integración por partes para la integral que involucra estas dos funciones es:

$$∫u\,dv=uv−∫v\,du. \label{IBP}$$

La ventaja de usar la fórmula de integración por partes es que podemos usarla para intercambiar una integral por otra, posiblemente más fácil, integral. El siguiente ejemplo ilustra su uso.

Ejemplo$\PageIndex{1}$: Using Integration by Parts

Utilizar la integración por partes con$u=x$ y$dv=\sin x\,\,dx$ para evaluar

$$∫x\sin x\,\,dx. \nonumber$$

Solución

Al elegir$u=x$, tenemos$du=1\,\,dx$. Ya que$dv=\sin x\,\,dx$, obtenemos

$$v=∫\sin x\,\,dx=−\cos x. \nonumber$$

Es útil realizar un seguimiento de estos valores de la siguiente manera:

• $u=x$
• $dv=\sin x\,\,dx$
• $du=1\,dx$
• $v=∫\sin x\,\,dx=−\cos x.$

La aplicación de la fórmula de integración por partes (Ecuación\ ref {IBP}) da como resultado

$$\begin{align} ∫x\sin x\,\,dx &=(x)(−\cos x)−∫(−\cos x)(1\,\,dx) \tag{Substitute} \\[4pt] &=−x\cos x+∫\cos x\,\,dx \tag{Simplify} \end{align}$$

A continuación, use

$$∫\cos x\,\,dx =\sin x+C. \nonumber$$

para obtener

$$∫x\sin x\,\,dx =−x\cos x+\sin x+C. \nonumber$$

Análisis

En este punto, probablemente hay algunos elementos que necesitan aclaración. En primer lugar, puede que tengas curiosidad sobre lo que hubiera pasado si hubiéramos elegido$u=\sin x$ y$dv=x$. Si lo hubiéramos hecho, entonces tendríamos$du=\cos x$ y$v=\dfrac{1}{2}x^2$. Así, después de aplicar la integración por partes (Ecuación\ ref {IBP}), tenemos

$$∫​x\sin x\,\,dx=\dfrac{1}{2}x^2\sin x−∫\dfrac{1}{2}x^2\cos x\,\,dx. \nonumber$$

Desafortunadamente, con la nueva integral, no estamos en mejor posición que antes. Es importante tener en cuenta que cuando aplicamos la integración por partes, es posible que tengamos que probar varias opciones para$u$ y$dv$ antes de encontrar una elección que funcione.

Segundo, tal vez te preguntes por qué$v=∫​\sin x\,\,dx=−\cos x$, cuando nos encontramos, no usamos$v=−\cos x+K.$ Para ver que no hace diferencia, podemos reelaborar el problema usando$v=−\cos x+K$:

$$\begin{align*} ∫x\sin x\,\,dx &=(x)(−\cos x+K)−∫(−\cos x+K)(1\,\,dx) \\[4pt] &=−x\cos x+Kx+∫\cos x\,\,dx−∫K\,\,dx \\[4pt] &=−x\cos x+Kx+\sin x−Kx+C \\[4pt] &=−x\cos x+\sin x+C. \end{align*}$$

Como puede ver, no hace diferencia en la solución final.

Por último, podemos verificar para asegurarnos de que nuestro antiderivado es correcto diferenciando$−x\cos x+\sin x+C:$

$$\begin{align*} \dfrac{d}{\,dx}(−x\cos x+\sin x+C) = \cancel{(−1)\cos x} + (−x)(−\sin x) + \cancel{\cos x} \\[4pt] =x\sin x \end{align*}$$

Por lo tanto, el antiderivado comprueba.

Ejercicio$\PageIndex{1}$

Evaluar$∫​xe^{2x}\,dx$ usando la fórmula de integración por partes (Ecuación\ ref {IBP}) con$u=x$ y$dv=e^{2x}\,\,dx$.

Pista

Encuentra$du$ y$v$, y usa el ejemplo anterior como guía.

Contestar

$$∫​xe^{2x}\,\,dx=\dfrac{1}{2}xe^{2x}−\dfrac{1}{4}e^{2x}+C \nonumber$$

La pregunta natural a hacer en este punto es: ¿Cómo sabemos elegir$u$ y$dv$? A veces es cuestión de prueba y error; sin embargo, el acrónimo LIATE muchas veces puede ayudar a eliminar algunas de las conjeturas de nuestras elecciones. Este acrónimo significa L funciones ogarítmicas, I nverso Funciones trigonométricas, Funciones A lgebraicas, T funciones rigonométricas y E funciones xponenciales. Esta mnemotécnica sirve como una ayuda para determinar una elección apropiada para$u$. El tipo de función en la integral que aparece primero en la lista debe ser nuestra primera elección de$u$.

Por ejemplo, si una integral contiene una función logarítmica y una función algebraica, deberíamos$u$ elegir ser la función logarítmica, porque L viene antes que A en LIATE. La integral en Ejemplo$\PageIndex{1}$ tiene una función trigonométrica ($\sin x$) y una función algebraica ($x$). Debido a que A viene antes que T en LIATE,$u$ elegimos ser la función algebraica. Cuando hemos elegido$u$,$dv$ se selecciona para ser la parte restante de la función a integrar, junto con$\,dx$.

¿Por qué funciona este mnemotécnico? Recuerden que lo que escojamos ser$dv$ debe ser algo que podamos integrar. Dado que no contamos con fórmulas de integración que nos permitan integrar funciones logarítmicas simples y funciones trigonométricas inversas, tiene sentido que no se elijan como valores para$dv$. En consecuencia, deberían estar a la cabeza de la lista como opciones para$u$. Así, pusimos LI al inicio del mnemotécnico. (Con la misma facilidad podríamos haber comenzado con IL, ya que estos dos tipos de funciones no aparecerán juntas en un problema de integración por partes). Las funciones exponenciales y trigonométricas están al final de nuestra lista porque son bastante fáciles de integrar y tomar buenas decisiones para$dv$. Así, tenemos TE al final de nuestro mnemotécnico. (Con la misma facilidad podríamos haber usado ET al final, ya que cuando este tipo de funciones aparecen juntas generalmente no importa realmente cuál es$u$ y cuál es$dv$.) Las funciones algebraicas son generalmente fáciles tanto de integrar como de diferenciar, y vienen en medio de la mnemotécnica.

Ejemplo$\PageIndex{2}$: Using Integration by Parts

Evaluar $$∫\dfrac{\ln x}{x^3}\,\,dx. \nonumber$$

Solución

Comience por reescribir la integral:

$$∫\dfrac{\ln x}{x^3}\,\,dx=∫​x^{−3}\ln x\,\,dx. \nonumber$$

Ya que esta integral contiene la función algebraica$x^{−3}$ y la función logarítmica$\ln x$, elija$u=\ln x$, ya que$L$ viene antes que A en LIATE. Después de haber elegido$u=\ln x$, debemos elegir$dv=x^{−3}\,dx$.

Siguiente, ya que$u=\ln x,$ tenemos$du=\dfrac{1}{x}\,dx.$ También,$v=∫​x^{−3}\,dx=−\dfrac{1}{2}x^{−2}.$ Resumiendo,

• $u=\ln x$
• $du=\dfrac{1}{x}\,dx$
• $dv=x^{−3}\,dx$
• $v=∫​x^{−3}\,dx=−\dfrac{1}{2}x^{−2}.$

Sustituir en la fórmula de integración por partes (Ecuación\ ref {IBP}) da

$$\begin{align*} ∫\dfrac{\ln x}{x^3}\,dx &=∫​x^{−3}\ln x\,dx=(\ln x)(−\dfrac{1}{2}x^{−2})−∫​(−\dfrac{1}{2}x^{−2})(\dfrac{1}{x}\,dx) \\[4pt] &=−\dfrac{1}{2}x^{−2}\ln x+∫\dfrac{1}{2}x^{−3}\,\,dx \\[4pt] &=−\dfrac{1}{2}x^{−2}\ln x−\dfrac{1}{4}x^{−2}+C\ \\[4pt] &=−\dfrac{1}{2x^2}\ln x−\dfrac{1}{4x^2}+C \end{align*} \nonumber$$

Ejercicio$\PageIndex{2}$

Evaluar $$∫​x\ln x \,\,dx. \nonumber$$

Pista

Uso$u=\ln x$ y$dv=x\,\,dx$.

Contestar

$$∫​x\ln x \,\,dx=\dfrac{1}{2}x^2\ln x−\dfrac{1}{4}x^2+C \nonumber$$

En algunos casos, como en los dos ejemplos siguientes, puede ser necesario aplicar la integración por partes más de una vez.

Ejemplo$\PageIndex{3A}$: Applying Integration by Parts More Than Once

Evaluar $$∫​x^2e^{3x}\,dx. \nonumber$$

Solución

Usando LIATE, elija$u=x^2$ y$dv=e^{3x}\,dx$. Así,$du=2x\,dx$ y$v=∫e^{3x}\,dx=\left(\dfrac{1}{3}\right)e^{3x}$. Por lo tanto,

• $u=x^2$
• $du=2x\,dx$
• $dv=e^{3x}\,dx$
• $v=∫e^{3x}\,dx=\dfrac{1}{3}e^{3x}.$

Sustituir en Ecuación\ ref {IBP} produce

$$∫x^2e^{3x}\,dx=\dfrac{1}{3}x^2e^{3x}−∫\dfrac{2}{3}xe^{3x}\,dx. \label{3A.2}$$

Todavía no podemos integrarnos$∫\dfrac{2}{3}xe^{3x}\,dx$ directamente, pero la integral ahora tiene un menor poder encendido$x$. Podemos evaluar esta nueva integral utilizando nuevamente la integración por partes. Para ello, elija

$$u=x \nonumber$$

y

$$dv=\dfrac{2}{3}e^{3x}\,dx. \nonumber$$

Por lo tanto,

$$du=\,dx \nonumber$$

y

$$v=∫\left(\dfrac{2}{3}\right)e^{3x}\,dx=\left(\dfrac{2}{9}\right)e^{3x}. \nonumber$$

Ahora tenemos

• $u=x$
• $du=\,dx$
• $dv=\dfrac{2}{3}e^{3x}\,dx$
• $\displaystyle v=∫\dfrac{2}{3}e^{3x}\,dx=\dfrac{2}{9}e^{3x}.$

Sustituyendo de nuevo en la ecuación\ ref {3A.2} rendimientos

$$∫​x^2e^{3x}\,dx=\dfrac{1}{3}x^2e^{3x}−\left(\dfrac{2}{9}xe^{3x}−∫\dfrac{​2}{9}e^{3x}\,dx\right). \nonumber$$

Después de evaluar la última integral y simplificar, obtenemos

$$∫x^2e^{3x}\,dx=\dfrac{1}{3}x^2e^{3x}−\dfrac{2}{9}xe^{3x}+\dfrac{2}{27}e^{3x}+C. \nonumber$$

Ejemplo$\PageIndex{3B}$: Applying Integration by Parts When LIATE Does not Quite Work

Evaluar

$$∫​t^3e^{t^2}dt. \nonumber$$

Solución

Si utilizamos una interpretación estricta del LIATE mnemotécnico para hacer nuestra elección$u$, terminamos con$u=t^3$ y$dv=e^{t^2}dt$. Desafortunadamente, esta elección no va a funcionar porque no podemos evaluar$∫​e^{t^2}dt$. Sin embargo, ya que podemos evaluar$∫​te^{t^2}\,dx$, podemos intentar elegir$u=t^2$ y$dv=te^{t^2}dt.$ Con estas opciones tenemos

• $u=t^2$
• $du=2tdt$
• $dv=te^{t^2}dt$
• $v=∫​te^{t^2}dt=\dfrac{1}{2}e^{t^2}.$

Por lo tanto, obtenemos

$$\begin{align*} ∫t^3e^{t^2}dt =\dfrac{1}{2}t^2e^{t^2}−∫\dfrac{1}{2}e^{t^2}2t\,dt \\[4pt] =\dfrac{1}{2}t^2e^{t^2}−\dfrac{1}{2}e^{t^2}+C. \end{align*}$$

Ejemplo$\PageIndex{3C}$: Applying Integration by Parts More Than Once

Evaluar $$∫​\sin (\ln x)\,dx. \nonumber$$

Solución

Esta integral parece tener solo una función —es decir,$\sin (\ln x)$ —sin embargo, siempre podemos usar la función constante 1 como la otra función. En este ejemplo, vamos a elegir$u=\sin (\ln x)$ y$dv=1\,dx$. (La decisión de usar$u=\sin (\ln x)$ es fácil. No podemos elegir$dv=\sin (\ln x)\,dx$ porque si pudiéramos integrarlo, ¡no estaríamos usando la integración por partes en primer lugar!) Consecuentemente,$du=(1/x)\cos (\ln x) \,dx$ y$v=∫​ 1 \,dx=x.$ Después de aplicar la integración por partes a la integral y simplificar, tenemos

$$∫​\sin \left(\ln x\right) \,dx=x \sin (\ln x)−\int \cos (\ln x)\,dx. \nonumber$$

Desafortunadamente, este proceso nos deja con una nueva integral que es muy similar a la original. No obstante, veamos qué sucede cuando volvemos a aplicar la integración por partes. Esta vez vamos a elegir$u=\cos (\ln x)$ y$dv=1\,dx,$ hacer$du=−(1/x)\sin (\ln x)\,dx$ y$v=∫​1\,dx=x.$

Sustituyendo, tenemos

$$∫​\sin (\ln x)\,dx=x \sin (\ln x)−(x \cos (\ln x)-∫​−\sin (\ln x)\,dx). \nonumber$$

Después de simplificar, obtenemos

$$∫​\sin (\ln x)\,dx=x\sin (\ln x)−x \cos (\ln x)−∫​\sin (\ln x)\,dx. \nonumber$$

La última integral es ahora la misma que la original. Puede parecer que simplemente hemos ido en círculo, pero ahora podemos evaluar realmente la integral. Para ver cómo hacer esto con mayor claridad, sustituya$I=∫​\sin (\ln x)\,dx.$ Así, la ecuación se convierte

$$I=x \sin (\ln x)−x \cos (\ln x)−I. \nonumber$$

Primero, agregue$I$ a ambos lados de la ecuación para obtener

$$2I=x \sin (\ln x)−x \cos (\ln x). \nonumber$$

A continuación, divídala por 2:

$$I=\dfrac{1}{2}x \sin (\ln x)−\dfrac{1}{2}x \cos (\ln x). \nonumber$$

Sustituyendo de$I=∫​\sin (\ln x)\,dx$ nuevo, tenemos

$$\int \sin (\ln x) \,dx=\dfrac{1}{2}x \sin (\ln x)−\dfrac{1}{2}x \cos (\ln x). \nonumber$$

De esto vemos que$(1/2)x \sin (\ln x)−(1/2)x \cos (\ln x)$ es un antiderivado de$\sin (\ln x)\,dx$. Para el antiderivado más general, agregue$+C$:

$$∫ \sin (\ln x) \,dx=\dfrac{1}{2}x \sin (\ln x)−\dfrac{1}{2}x \cos (\ln x)+C. \nonumber$$

Análisis

Si este método se siente un poco extraño al principio, podemos verificar la respuesta por diferenciación:

$$\begin{align*} \dfrac{d}{\,dx}\left(\dfrac{1}{2}x \sin (\ln x)−\dfrac{1}{2}x\cos (\ln x)\right) \\[4pt] &=\dfrac{1}{2}(\sin (\ln x))+\cos (\ln x)⋅\dfrac{1}{x}⋅\dfrac{1}{2}x−\left(\dfrac{1}{2}\cos (\ln x)−\sin (\ln x)⋅\dfrac{1}{x}⋅\dfrac{1}{2}x\right) \\[4pt] &=\sin (\ln x). \end{align*}$$

Ejercicio$\PageIndex{3}$

Evaluar $$∫x^2\sin x\,dx. \nonumber$$

Insinuación

Esto es similar a Ejemplos$\PageIndex{3A}$ -$\PageIndex{3C}$.

Contestar

$$∫x^2\sin x\,dx=−x^2\cos x+2x\sin x+2\cos x+C \nonumber$$

Integración por Partes para Integrales Definidas

Ahora que hemos utilizado con éxito la integración por partes para evaluar integrales indefinidas, dirigimos nuestra atención a integrales definidas. La técnica de integración es realmente la misma, solo que agregamos un paso para evaluar la integral en los límites superior e inferior de la integración.

Integración por Partes para Integrales Definidas

Dejar$u=f(x)$ y$v=g(x)$ ser funciones con derivadas continuas en [$a,b$]. Entonces

$$∫^b_a u\,dv=uv\Big|^b_a−∫^b_a v\, du \nonumber$$

Ejemplo$\PageIndex{4A}$: Finding the Area of a Region

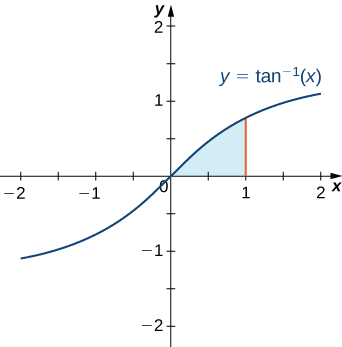
Encuentra el área de la región delimitada arriba por la gráfica de$y=\tan^{−1}x$ y abajo por el$x$ eje -sobre el intervalo [$0,1$].

Solución

Esta región se muestra en la Figura$\PageIndex{1}$. Para encontrar el área, debemos evaluar

$$∫^1_0 \tan^{−1}x\, \,dx. \nonumber$$

Figura$\PageIndex{1}$: Para encontrar el área de la región sombreada, tenemos que utilizar la integración por partes.

Para esta integral, vamos a elegir$u=tan^{−1}x$ y$dv=\,dx$, con ello haciendo$du=\dfrac{1}{x^2+1}\,dx$ y$v=x$. Después de aplicar la fórmula de integración por partes (Ecuación\ ref {IBP}) obtenemos

$$\text{Area}=\left. x \tan^{−1} x \right|^1_0−∫^1_0 \dfrac{x}{x^2+1} \,dx. \nonumber$$

Use$u$ -sustitución para obtener

$$∫^1_0\dfrac{x}{x^2+1}\,dx=\left.\dfrac{1}{2}\ln \left(x^2+1\right) \right|^1_0. \nonumber$$

Por lo tanto,

$$\text{Area}=x \tan^{−1}x \Big|^1_0− \left.\dfrac{1}{2}\ln \left( x^2+1 \right) \right|^1_0=\left(\dfrac{π}{4}−\dfrac{1}{2}\ln 2\right) \,\text{units}^2. \nonumber$$

En este punto podría no ser mala idea hacer un “chequeo de la realidad” sobre la razonabilidad de nuestra solución. Desde$\dfrac{π}{4}−\dfrac{1}{2}\ln 2≈0.4388\,\text{units}^2,$ y de Figura$\PageIndex{1}$ esperamos que nuestra zona sea un poco menor de lo que$0.5\,\text{units}^2,$ esta solución parece ser razonable.

Ejemplo$\PageIndex{4B}$: Finding a Volume of Revolution

Encuentre el volumen del sólido obtenido al girar la región delimitada por la gráfica del$f(x)=e^{−x},$$x$ eje -eje, el$y$ eje -y la línea$x=1$ alrededor del$y$ eje -eje.

Solución

La mejor opción para resolver este problema es usar el método shell. Comience por esbozar la región a girar, junto con un rectángulo típico (Figura$\PageIndex{2}$).

Figura$\PageIndex{2}$: Podemos usar el método shell para encontrar un volumen de revolución.

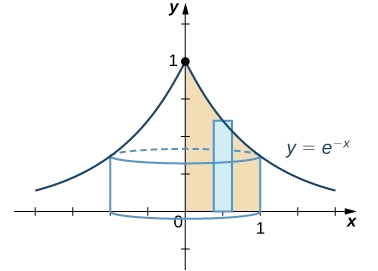
Para encontrar el volumen usando conchas, debemos evaluar

$$2π∫^1_0xe^{−x}\,dx. \label{4B.1}$$

Para ello, vamos$u=x$ y$dv=e^{−x}$. Estas opciones conducen a$du=\,dx$ y$v=∫​e^{−x}\,dx=−e^{−x}.$ Usando la fórmula del Método Shell, obtenemos

\ [\ begin {align*}\ text {Volumen} &=2π^1_0xe^ {−x}\, dx\\ [4pt] = 2π\ left (−xe^ {−x}\ big|^1_0+^1_0e^ {−x}\, dx\ derecha)\ tag {Usar integración por partes}\\ [4pt]
&= 2π\ izquierda (-e^ {-1} + 0 - e^ {-x}\ Big|^1_0\ derecha)\\ [4pt]
&= 2π\ izquierda (-e^ {-1} - e^ {-1} + 1\ derecha)\\ [4pt]
&= 2π\ izquierda (1 -\ dfrac {2} {e}\ derecha)\,\ texto {unidades} ^3. \ tag {Evaluar y simplificar}\ end {alinear*}\]

Análisis

Nuevamente, es una buena idea comprobar la razonabilidad de nuestra solución. Observamos que el sólido tiene un volumen ligeramente menor que el de un cilindro de radio$1$ y altura de$1/e$ agregado al volumen de un cono de radio base$1$ y altura de$1−\dfrac{1}{e}.$ Consecuentemente, el sólido debe tener un volumen un poco menor que

$$π(1)^2\dfrac{1}{e}+\left(\dfrac{π}{3}\right)(1)^2\left(1−\dfrac{1}{e}\right)=\dfrac{2π}{3e}+\dfrac{π}{3}≈1.8177\,\text{units}^3. \nonumber$$

Ya que$2π−\dfrac{4π}{e}≈1.6603,$ vemos que nuestro volumen calculado es razonable.

Ejercicio$\PageIndex{4}$

Evaluar $$∫^{π/2}_0x\cos x\,dx. \nonumber$$

Pista

Utilice la ecuación\ ref {IBP} con$u=x$ y$dv=\cos x\,dx.$

Contestar

$$∫^{π/2}_0x\cos x\,dx = \dfrac{π}{2}−1 \nonumber$$

Conceptos clave

• La fórmula de integración por partes (Ecuación\ ref {IBP}) permite el intercambio de una integral por otra, posiblemente más fácil, integral.
• La integración por partes se aplica tanto a integrales definidas como indefinidas.

Ecuaciones Clave

• Integración por fórmula de piezas

$\displaystyle ∫u\,dv=uv−∫v\,du$

• Integración por partes para integrales definidas

$\displaystyle ∫^b_au\,dv=uv\Big|^b_a−∫^b_av\,du$

Glosario

integración por partes

una técnica de integración que permite el intercambio de una integral por otra usando la fórmula$\displaystyle ∫​u\,dv=uv−∫​v\,du$