7.4: Fracciones Parciales
- Page ID
- 116457
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Integrar una función racional utilizando el método de fracciones parciales.
- Reconocer factores lineales simples en una función racional.
- Reconocer factores lineales repetidos en una función racional.
- Reconocer los factores cuadráticos en una función racional.
Hemos visto algunas técnicas que nos permiten integrar funciones racionales específicas. Por ejemplo, sabemos que
\[ \int \dfrac{du}{u}=\ln |u|+C \nonumber \]
y
\[ \int \dfrac{du}{u^2+a^2}=\dfrac{1}{a}\tan^{−1} \left(\dfrac{u}{a}\right)+C.\nonumber \]
Sin embargo, todavía no contamos con una técnica que nos permita abordar cocientes arbitrarios de este tipo. Por lo tanto, no es inmediatamente obvio cómo hacer la evaluación
\[ \int \dfrac{3x}{x^2−x−2}\,dx.\nonumber \]
Sin embargo, sabemos por material previamente desarrollado que
\[ \int \left(\dfrac{1}{x+1}+\dfrac{2}{x−2}\right)\,dx=\ln |x+1|+2\ln |x−2|+C.\nonumber \]
De hecho, al obtener un denominador común, vemos que
\[ \dfrac{1}{x+1}+\dfrac{2}{x−2}=\dfrac{3x}{x^2−x−2}.\nonumber \]
En consecuencia,
\[ \int \dfrac{3x}{x^2−x−2}\,dx=\int \left(\dfrac{1}{x+1}+\dfrac{2}{x−2}\right)\,dx.\nonumber \]
En esta sección, examinamos el método de descomposición parcial de la fracción, que nos permite descomponer funciones racionales en sumas de funciones racionales más simples, más fácilmente integradas. Usando este método, podemos reescribir una expresión como:
\[ \dfrac{3x}{x^2−x−2}\nonumber \]
como una expresión como
\[ \dfrac{1}{x+1}+\dfrac{2}{x−2}.\nonumber \]
La clave del método de descomposición parcial de la fracción es poder anticipar la forma que tomará la descomposición de una función racional. Como veremos, esta forma es predecible y altamente dependiente de la factorización del denominador de la función racional. También es sumamente importante tener en cuenta que la descomposición parcial de la fracción se puede aplicar a una función racional\( \dfrac{P(x)}{Q(x)}\) sólo si\( deg(P(x))<deg(Q(x))\). En el caso cuando\( deg(P(x))≥deg(Q(x))\), primero debemos realizar división larga para reescribir el cociente\( \dfrac{P(x)}{Q(x)}\) en la forma\( A(x)+\dfrac{R(x)}{Q(x)}\), donde\( deg(R(x))<deg(Q(x))\). Luego hacemos una descomposición parcial de la fracción en\( \dfrac{R(x)}{Q(x)}\). El siguiente ejemplo, aunque no requiere descomposición parcial de la fracción, ilustra nuestro acercamiento a integrales de funciones racionales de la forma\( \int \dfrac{P(x)}{Q(x)}\,dx\), donde\( deg(P(x))≥deg(Q(x)).\)
Evaluar
\[ \int \dfrac{x^2+3x+5}{x+1}\,dx. \nonumber \]
Solución
Ya\( deg(x^2+3x+5)≥deg(x+1),\) que realizamos división larga para obtener
\[ \dfrac{x^2+3x+5}{x+1}=x+2+\dfrac{3}{x+1}. \nonumber \]
Por lo tanto,
\[ \int \dfrac{x^2+3x+5}{x+1}\,dx=\int \left(x+2+\dfrac{3}{x+1}\right)\,dx=\dfrac{1}{2}x^2+2x+3\ln |x+1|+C. \nonumber \]
Visite este sitio web para una revisión de la división larga de polinomios.
Evaluar
\[ \int \dfrac{x−3}{x+2}\,dx. \nonumber \]
- Pista
-
Utilice división larga para obtener\( \dfrac{x−3}{x+2}=1−\dfrac{5}{x+2}. \nonumber \)
- Contestar
-
\[ x−5\ln |x+2|+C \nonumber \]
Para integrar\(\displaystyle \int \dfrac{P(x)}{Q(x)}\,dx\), donde\( deg(P(x))<deg(Q(x))\), debemos comenzar por factorizar\( Q(x)\).
Factores lineales no repetidos
Si se\( Q(x)\) puede factorizar como\( (a_1x+b_1)(a_2x+b_2)…(a_nx+b_n)\), donde cada factor lineal es distinto, entonces es posible encontrar constantes\( A_1,A_2,…A_n\) satisfactorias
\[ \dfrac{P(x)}{Q(x)}=\dfrac{A_1}{a_1x+b_1}+\dfrac{A_2}{a_2x+b_2}+⋯+\dfrac{A_n}{a_nx+b_n}. \label{eq:7.4.1} \]
La prueba de que tales constantes existen está fuera del alcance de este curso.
En este siguiente ejemplo, vemos cómo utilizar fracciones parciales para integrar una función racional de este tipo.
Evaluar\(\displaystyle \int \dfrac{3x+2}{x^3−x^2−2x}\,dx.\)
Solución
Ya que\( deg(3x+2)<deg(x^3−x^2−2x)\), comenzamos por factorizar el denominador de\( \dfrac{3x+2}{x^3−x^2−2x}\). Eso lo podemos ver\( x^3−x^2−2x=x(x−2)(x+1)\). Así, hay constantes\(A\),\(B\), y la ecuación\( C\) satisfactoria\ ref {eq:7.4.1} tal que
\[ \dfrac{3x+2}{x(x−2)(x+1)}=\dfrac{A}{x}+\dfrac{B}{x−2}+\dfrac{C}{x+1}. \nonumber \]
Ahora debemos encontrar estas constantes. Para ello, comenzamos por conseguir un denominador común a la derecha. Por lo tanto,
\[ \dfrac{3x+2}{x(x−2)(x+1)}=\dfrac{A(x−2)(x+1)+Bx(x+1)+Cx(x−2)}{x(x−2)(x+1)}. \nonumber \]
Ahora, establecemos los numeradores iguales entre sí, obteniendo
\[ 3x+2=A(x−2)(x+1)+Bx(x+1)+Cx(x−2).\label{Ex2Numerator} \]
Existen dos estrategias diferentes para encontrar los coeficientes\(A\),\(B\), y\(C\). Nos referimos a estos como el método de equiparación de coeficientes y el método de sustitución estratégica.
Estrategia uno: Método de igualación de coeficientes
Reescribir la ecuación\(\ref{Ex2Numerator}\) en la forma
\[ 3x+2=(A+B+C)x^2+(−A+B−2C)x+(−2A). \nonumber \]
Equiparar coeficientes produce el sistema de ecuaciones
\[\begin{align*} A+B+C &=0 \\[4pt] −A+B−2C &= 3 \\[4pt] −2A &=2. \end{align*}\]
Para resolver este sistema, primero observamos que\( −2A=2⇒A=−1.\) Sustituir este valor en las dos primeras ecuaciones nos da el sistema
\( B+C=1\)
\( B−2C=2\).
Multiplicar la segunda ecuación por\( −1\) y sumar la ecuación resultante a la primera produce
\( −3C=1,\)
lo que a su vez implica eso\( C=−\dfrac{1}{3}\). Sustituir este valor en la ecuación\( B+C=1\) rinde\( B=\dfrac{4}{3}\). Así, resolver estas ecuaciones rinde\( A=−1, B=\dfrac{4}{3}\), y\( C=−\dfrac{1}{3}\).
Es importante señalar que el sistema producido por este método es consistente si y sólo si hemos configurado correctamente la descomposición. Si el sistema es inconsistente, hay un error en nuestra descomposición.
Estrategia dos: Método de Sustitución Estratégica
El método de sustitución estratégica se basa en el supuesto de que hemos configurado correctamente la descomposición. Si la descomposición se configura correctamente, entonces debe haber valores de\( A, B,\) y\( C\) que satisfagan Ecuación\(\ref{Ex2Numerator}\) para todos los valores de\( x\). Es decir, esta ecuación debe ser cierta para cualquier valor de\( x\) que nos importe sustituir en ella. Por lo tanto, al elegir valores de\( x\) cuidado y sustituirlos en la ecuación, podemos encontrar\( A, B\), y\( C\) fácilmente. Por ejemplo, si sustituimos\( x=0\), la ecuación se reduce a\( 2=A(−2)(1)\). Resolviendo\( A\) rendimientos\( A=−1\). A continuación, al sustituir\( x=2\), la ecuación se reduce a\( 8=B(2)(3)\), o de manera equivalente\( B=4/3\). Por último, sustituimos\( x=−1\) en la ecuación y obtenemos\( −1=C(−1)(−3).\) Resolviendo, tenemos\( C=−\dfrac{1}{3}\).
Es importante tener en cuenta que si intentamos utilizar este método con una descomposición que no se ha configurado correctamente, aún podemos encontrar valores para las constantes, pero estas constantes carecen de sentido. Si optamos por utilizar el método de sustitución estratégica, entonces es una buena idea verificar el resultado recombinando los términos algebraicamente.
Ahora que tenemos los valores de\( A, B,\) y\( C,\) reescribimos la integral original:
\[ \int \dfrac{3x+2}{x^3−x^2−2x}\,dx=\int \left(−\dfrac{1}{x}+\dfrac{4}{3}⋅\dfrac{1}{x−2}−\dfrac{1}{3}⋅\dfrac{1}{x+1}\right)\,dx. \nonumber \]
Evaluar la integral nos da
\[ \int \dfrac{3x+2}{x^3−x^2−2x}\,dx=−\ln |x|+\dfrac{4}{3}\ln |x−2|−\dfrac{1}{3}\ln |x+1|+C. \nonumber \]
En el siguiente ejemplo, integramos una función racional en la que el grado del numerador no es menor que el grado del denominador.
Evaluar\(\displaystyle \int \dfrac{x^2+3x+1}{x^2−4}\,dx.\)
Solución
Ya que\( deg(x^2+3x+1)≥deg(x^2−4),\) debemos realizar una larga división de polinomios. Esto da como resultado
\[ \dfrac{x^2+3x+1}{x^2−4}=1+\dfrac{3x+5}{x^2−4} \nonumber \]
A continuación, realizamos la descomposición parcial de la fracción en\( \dfrac{3x+5}{x^2−4}=\dfrac{3x+5}{(x+2)(x−2)}\). Tenemos
\[ \dfrac{3x+5}{(x−2)(x+2)}=\dfrac{A}{x−2}+\dfrac{B}{x+2}. \nonumber \]
Por lo tanto,
\[ 3x+5=A(x+2)+B(x−2). \nonumber \]
Resolviendo\( A\) y\( B\) usando cualquiera de los dos métodos, obtenemos\( A=11/4\) y\( B=1/4.\)
Reescribiendo la integral original, tenemos
\[ \int \dfrac{x^2+3x+1}{x^2−4}\,dx=\int \left(1+\dfrac{11}{4}⋅\dfrac{1}{x−2}+\dfrac{1}{4}⋅\dfrac{1}{x+2}\right)\,dx. \nonumber \]
Evaluar los productos integrales
\[ \int \dfrac{x^2+3x+1}{x^2−4}\,dx=x+\dfrac{11}{4}\ln |x−2|+\dfrac{1}{4}\ln |x+2|+C. \nonumber \]
Como vemos en el siguiente ejemplo, puede ser posible aplicar la técnica de descomposición parcial de fracciones a una función no racional. El truco es convertir la función no racional en una función racional a través de una sustitución.
Evaluar\(\displaystyle \int \dfrac{\cos x}{\sin^2x−\sin x}\,dx.\)
Solución
Empecemos por dejar\( u=\sin x.\) Consecuentemente,\( du=\cos x\,dx.\) Después de hacer estas sustituciones, tenemos
\[ \int \dfrac{\cos x}{\sin^2x−\sin x}\,dx=\int \dfrac{du}{u^2−u}=\int \dfrac{du}{u(u−1)}. \nonumber \]
Aplicación de la descomposición parcial de la fracción a\(\dfrac{1}{u(u−1)}\) da\( \dfrac{1}{u(u−1)}=−\dfrac{1}{u}+\dfrac{1}{u−1}.\)
Por lo tanto,
\[ \int \dfrac{\cos x}{\sin^2x−\sin x}\,dx=−\ln |u|+\ln |u−1|+C=−\ln |\sin x|+\ln |\sin x−1|+C. \nonumber \]
Evaluar\(\displaystyle \int \dfrac{x+1}{(x+3)(x−2)}\,dx.\)
- Pista
-
\[ \dfrac{x+1}{(x+3)(x−2)}=\dfrac{A}{x+3}+\dfrac{B}{x−2} \nonumber \]
- Contestar
-
\[ \dfrac{2}{5}\ln |x+3|+\dfrac{3}{5}\ln |x−2|+C \nonumber \]
Factores lineales repetidos
Para algunas aplicaciones, necesitamos integrar expresiones racionales que tengan denominadores con factores lineales repetidos, es decir, funciones racionales con al menos un factor de la forma\( (ax+b)^n,\) donde\( n\) es un entero positivo mayor o igual a\( 2\). Si el denominador contiene el factor lineal repetido\( (ax+b)^n\), entonces la descomposición debe contener
\[ \dfrac{A_1}{ax+b}+\dfrac{A_2}{(ax+b)^2}+⋯+\dfrac{A_n}{(ax+b)^n}. \label{eq:7.4.2} \]
Como vemos en nuestro siguiente ejemplo, la técnica básica utilizada para resolver para los coeficientes es la misma, pero requiere más álgebra para determinar los numeradores de las fracciones parciales.
Evaluar\(\displaystyle \int \dfrac{x−2}{(2x−1)^2(x−1)}\,dx.\)
Solución
Tenemos\( deg(x−2)<deg((2x−1)^2(x−1)),\) para que podamos proceder con la descomposición. Dado que\( (2x−1)^2\) es un factor lineal repetido, incluir
\[ \dfrac{A}{2x−1}+\dfrac{B}{(2x−1)^2} \nonumber \]
en la descomposición en la Ecuación\ ref {eq:7.4.2}. Por lo tanto,
\[ \dfrac{x−2}{(2x−1)^2(x−1)}=\dfrac{A}{2x−1}+\dfrac{B}{(2x−1)^2}+\dfrac{C}{x−1}. \nonumber \]
Después de obtener un denominador común e igualar los numeradores, tenemos
\[ x−2=A(2x−1)(x−1)+B(x−1)+C(2x−1)^2. \label{Ex5Numerator} \]
Luego usamos el método de igualar coeficientes para encontrar los valores de\( A, B,\) y\( C\).
\[ x−2=(2A+4C)x^2+(−3A+B−4C)x+(A−B+C). \nonumber \]
Equiparar coeficientes rendimientos\( 2A+4C=0\),\(−3A+B−4C=1\), y\( A−B+C=−2\). Resolver este sistema rinde\( A=2, B=3,\) y\( C=−1.\)
Alternativamente, podemos utilizar el método de sustitución estratégica. En este caso, sustituyendo\( x=1\) y\( x=1/2\) en Ecuación produce\(\ref{Ex5Numerator}\) fácilmente los valores\( B=3\) y\( C=−1\). En este punto, puede parecer que nos hemos quedado sin buenas opciones para\( x\), sin embargo, ya que ya tenemos valores para\( B\) y\( C\), podemos sustituirlos en estos valores y elegir cualquier valor por\( x\) no utilizado anteriormente. El valor\( x=0\) es una buena opción. En este caso, obtenemos la ecuación\( −2=A(−1)(−1)+3(−1)+(−1)(−1)^2\) o, equivalentemente,\( A=2.\)
Ahora que tenemos los valores para\( A, B,\) y\( C\), reescribimos la integral original y la evaluamos:
\ [\ begin {align*}\ int\ dfrac {x−2} {(2x−1) ^2 (x−1)}\, dx &=\ int\ left (\ dfrac {2} {2x−1} +\ dfrac {3} {(2x−1) ^2} −\ dfrac {1} {x−1}\ derecha)\, dx\ [4pt]
&=\ ln |2x−1|−\ dfrac {3} {2 (2x−1)} −\ ln |x−1|+C.\ end {align*}\]
Configurar la descomposición parcial de la fracción para
\[ \int \dfrac{x+2}{(x+3)^3(x−4)^2}\,dx. \nonumber \]
(No resolver los coeficientes ni completar la integración.)
- Pista
-
Utilice el método de resolución de problemas de Ejemplo como\( \PageIndex{5}\) guía.
- Contestar
-
\[ \dfrac{x+2}{(x+3)^3(x−4)^2}=\dfrac{A}{x+3}+\dfrac{B}{(x+3)^2}+\dfrac{C}{(x+3)^3}+\dfrac{D}{(x−4)}+\dfrac{E}{(x−4)^2} \nonumber \]
El Método General
Ahora que estamos empezando a hacernos una idea de cómo funciona la técnica de descomposición parcial de fracciones, describamos el método básico en la siguiente estrategia de resolución de problemas.
Para descomponer la función racional\( P(x)/Q(x)\), siga los siguientes pasos:
- Asegúrese de que\( deg(P(x))<deg(Q(x)).\) Si no, realizar división larga de polinomios.
- Factorizar\( Q(x)\) en el producto de factores cuadráticos lineales e irreducibles. Una cuadrática irreducible es una cuadrática que no tiene ceros reales.
- Suponiendo que\( deg(P(x))<deg(Q(x)\), los factores de\( Q(x)\) determinar la forma de la descomposición de\( P(x)/Q(x).\)
- Si se\( Q(x)\) puede factorizar como\( (a_1x+b_1)(a_2x+b_2)…(a_nx+b_n)\), donde cada factor lineal es distinto, entonces es posible encontrar constantes\( A_1,A_2,...A_n\) satisfactorias\[ \dfrac{P(x)}{Q(x)}=\dfrac{A_1}{a_1x+b_1}+\dfrac{A_2}{a_2x+b_2}+⋯+\dfrac{A_n}{a_nx+b_n}. \nonumber \]
- Si\( Q(x)\) contiene el factor lineal repetido\( (ax+b)^n\), entonces la descomposición debe contener\[ \dfrac{A_1}{ax+b}+\dfrac{A_2}{(ax+b)^2}+⋯+\dfrac{A_n}{(ax+b)^n}. \nonumber \]
- Por cada factor cuadrático irreducible\( ax^2+bx+c\) que\( Q(x)\) contenga, la descomposición debe incluir\[ \dfrac{Ax+B}{ax^2+bx+c}. \nonumber \]
- Por cada factor cuadrático irreducible repetido\( (ax^2+bx+c)^n,\) la descomposición debe incluir\[ \dfrac{A_1x+B_1}{ax^2+bx+c}+\dfrac{A_2x+B_2}{(ax^2+bx+c)^2}+⋯+\dfrac{A_nx+B_n}{(ax^2+bx+c)^n}. \nonumber \]
- Después de determinar la descomposición apropiada, resuelva para las constantes.
- Por último, reescribir la integral en su forma descompuesta y evaluarla utilizando técnicas previamente desarrolladas o fórmulas de integración.
Factores cuadráticos simples
Ahora veamos la integración de una expresión racional en la que el denominador contenga un factor cuadrático irreducible. Recordemos que la cuadrática\( ax^2+bx+c\) es irreducible si no\( ax^2+bx+c=0\) tiene ceros reales, es decir, si\( b^2−4ac<0.\)
Evaluar
\[ \int \dfrac{2x−3}{x^3+x}\,dx.\nonumber \]
Solución
Desde\( deg(2x−3)<deg(x^3+x),\) factorizar el denominador y proceder con la descomposición parcial de la fracción. Ya que\( x^3+x=x(x^2+1)\) contiene el factor cuadrático irreducible\( x^2+1\), incluir\( \dfrac{Ax+B}{x^2+1}\) como parte de la descomposición, junto con\( \dfrac{C}{x}\) para el término lineal\( x\). Así, la descomposición tiene la forma
\[ \dfrac{2x−3}{x(x^2+1)}=\dfrac{Ax+B}{x^2+1}+\dfrac{C}{x}.\nonumber \]
Después de obtener un denominador común e igualar los numeradores, obtenemos la ecuación
\[ 2x−3=(Ax+B)x+C(x^2+1).\nonumber \]
Resolviendo para\( A,B,\) y\( C,\) obtenemos\( A=3, B=2,\) y\( C=−3.\)
Por lo tanto,
\[ \dfrac{2x−3}{x^3+x}=\dfrac{3x+2}{x^2+1}−\dfrac{3}{x}.\nonumber \]
Sustituyendo de nuevo a la integral, obtenemos
\ [\ begin {align*}\ int\ dfrac {2x−3} {x^3+x}\, dx &=\ int\ izquierda (\ dfrac {3x+2} {x^2+1} −\ dfrac {3} {x}\ derecha)\, dx\ nonumber\\ [4pt]
&=3\ int\ dfrac {x} {x^2+1}\, dx+2\ int\ dfrac {1} {x^2+1}\, dx−3\ int\ dfrac {1} {x}\, dx & &\ text {Dividir la integral}\\ [4pt]
&=\ dfrac {3} {2}\ ln x^2 +1+2\ tan^ {−1} x−3\ ln |x|+C. & &\ text {Evaluar cada integral}\ end {align*}\]
Nota: Podemos reescribir\( \ln ∣x^2+1∣=\ln (x^2+1)\), si queremos hacerlo, ya que\( x^2+1>0.\)
Evaluar\(\displaystyle \int \dfrac{\,dx}{x^3−8}.\)
Solución: Podemos comenzar por factorizar\( x^3−8=(x−2)(x^2+2x+4).\) Vemos que el factor cuadrático\( x^2+2x+4\) es irreducible ya que\( 2^2−4(1)(4)=−12<0.\) Usando la descomposición descrita en la estrategia de resolución de problemas, obtenemos
\[ \dfrac{1}{(x−2)(x^2+2x+4)}=\dfrac{A}{x−2}+\dfrac{Bx+C}{x^2+2x+4}. \nonumber \]
Después de obtener un denominador común e igualar los numeradores, esto se convierte en
\[ 1=A(x^2+2x+4)+(Bx+C)(x−2). \nonumber \]
Aplicando cualquiera de los dos métodos, obtenemos\( A=\dfrac{1}{12},B=−\dfrac{1}{12},\) y\( C=−\dfrac{1}{3}.\)
Reescribiendo\( \int \dfrac{\,dx}{x^3−8},\) tenemos
\[ \int \dfrac{\,dx}{x^3−8}=\dfrac{1}{12}\int \dfrac{1}{x−2}\,dx−\dfrac{1}{12}\int \dfrac{x+4}{x^2+2x+4}\,dx. \nonumber \]
Podemos ver que
\[ \int \dfrac{1}{x−2}\,dx=\ln |x−2|+C,\nonumber \]
pero
\[ \int \dfrac{x+4}{x^2+2x+4}\,dx \nonumber \]
requiere un poco más de esfuerzo. Comencemos completando la plaza\( x^2+2x+4\) para obtener
\[ x^2+2x+4=(x+1)^2+3. \nonumber \]
Al dejar\( u=x+1\) y consecuentemente\( du=\,dx,\) vemos que
\ [\ begin {align*}\ int\ dfrac {x+4} {x^2+2x+4}\, dx &=\ int\ dfrac {x+4} {(x+1) ^2+3}\, dx & &\ text {Completa el cuadrado en el denominador}\\ [4pt]
&=\ int\ dfrac {u+3} {u^2+3}\, du &\ text {Sustituto} u=x+1,\, x=u−1,\ text {y} du=dx\\ [4pt]
&=\ int\ dfrac {u} {u^2+3 } du+\ int\ dfrac {3} {u^2+3} du & &\ text {Dividir el numerador aparte}\\ [4pt]
&=\ dfrac {1} {2}\ ln u^2+3+\ dfrac {3} {\ sqrt {3}}\ tan^ {−1}\ dfrac {u} {\ sqrt {3} +C & &\ text {Evaluar cada integral}\\ [4pt]
&=\ dfrac {1} {2}\ ln x^2+2x+4+\ sqrt {3}\ tan^ {−1}\ left (\ dfrac {x+1} {\ sqrt {3}}\ right) +C & &\ text {Reescribir en términos de} x\ texto {y simplificar}\ end {alinear*}\]
Sustituir de nuevo a la integral original y simplificar da
\[ \int \dfrac{ \,dx}{x^3−8}=\dfrac{1}{12}\ln |x−2|−\dfrac{1}{24}\ln |x^2+2x+4|−\dfrac{\sqrt{3}}{12}\tan^{−1}\left(\dfrac{x+1}{\sqrt{3}}\right)+C. \nonumber \]
Aquí de nuevo, podemos bajar el valor absoluto si queremos hacerlo, ya que\( x^2+2x+4>0\) para todos\( x\).
Encuentra el volumen del sólido de revolución obtenido al girar la región encerrada por la gráfica de\( f(x)=\dfrac{x^2}{(x^2+1)^2}\) y el eje x sobre el intervalo\( [0,1]\) alrededor del eje y.
Solución
Comencemos dibujando la región a girar (ver Figura\(\PageIndex{1}\)). Del boceto, vemos que el método shell es una buena opción para resolver este problema.
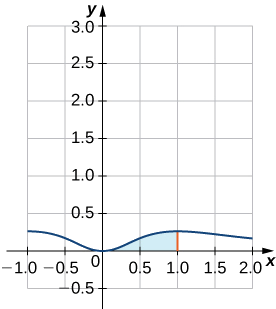
El volumen viene dado por
\[ V=2π\int ^1_0x⋅\dfrac{x^2}{(x^2+1)^2}\,dx=2π\int ^1_0\dfrac{x^3}{(x^2+1)^2}\,dx. \nonumber \]
Ya que\( deg((x^2+1)^2)=4>3=deg(x^3),\) podemos proceder con la descomposición parcial de la fracción. Tenga en cuenta que\( (x^2+1)^2\) es un cuadrático irreducible repetido. Usando la descomposición descrita en la estrategia de resolución de problemas, obtenemos
\[ \dfrac{x^3}{(x^2+1)^2}=\dfrac{Ax+B}{x^2+1}+\dfrac{Cx+D}{(x^2+1)^2}. \nonumber \]
Encontrar un denominador común e igualar los numeradores da
\[ x^3=(Ax+B)(x^2+1)+Cx+D. \nonumber \]
Resolviendo, obtenemos\( A=1, B=0, C=−1,\) y\( D=0.\) Sustituyendo de nuevo a la integral, tenemos
\[ V=2π\int _0^1\dfrac{x^3}{(x^2+1)^2}\,dx=2π\int _0^1\left(\dfrac{x}{x^2+1}−\dfrac{x}{(x^2+1)^2}\right)\,dx=2π\left(\dfrac{1}{2}\ln (x^2+1)+\dfrac{1}{2}⋅\dfrac{1}{x^2+1}\right)\Big|^1_0=π\left(\ln 2−\tfrac{1}{2}\right). \nonumber \]
Configurar la descomposición parcial de la fracción para\[ \int \dfrac{x^2+3x+1}{(x+2)(x−3)^2(x^2+4)^2}\,dx. \nonumber \]
- Pista
-
Utilice la estrategia de resolución de problemas.
- Contestar
-
\[ \dfrac{x^2+3x+1}{(x+2)(x−3)^2(x^2+4)^2}=\dfrac{A}{x+2}+\dfrac{B}{x−3}+\dfrac{C}{(x−3)^2}+\dfrac{Dx+E}{x^2+4}+\dfrac{Fx+G}{(x^2+4)^2} \nonumber \]
Conceptos clave
- La descomposición parcial de la fracción es una técnica utilizada para descomponer una función racional en una suma de funciones racionales simples que se pueden integrar utilizando técnicas aprendidas previamente.
- Al aplicar la descomposición parcial de la fracción, debemos asegurarnos de que el grado del numerador sea menor que el grado del denominador. Si no, necesitamos realizar una división larga antes de intentar la descomposición parcial de la fracción.
- La forma que tome la descomposición depende del tipo de factores en el denominador. Los tipos de factores incluyen factores lineales no repetidos, factores lineales repetidos, factores cuadráticos irreducibles no repetidos y factores cuadráticos irreducibles repetidos.
Glosario
- descomposición parcial de la fracción
- una técnica utilizada para descomponer una función racional en la suma de funciones racionales simples


