7.8: Capítulo 7 Ejercicios de revisión
- Page ID
- 116418
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En los ejercicios 1 - 4, determinar si la afirmación es verdadera o falsa. Justifica tu respuesta con una prueba o un contraejemplo.
1)\(\displaystyle ∫e^x\sin(x)\,dx\) no puede ser integrado por partes.
2)\(\displaystyle ∫\frac{1}{x^4+1}\,dx\) no se pueden integrar usando fracciones parciales.
- Contestar
- Falso
3) En la integración numérica, aumentar el número de puntos disminuye el error.
4) La integración por partes siempre puede producir la integral.
- Contestar
- Falso
En los ejercicios 5 - 10, evaluar la integral utilizando el método especificado.
5)\(\displaystyle ∫x^2\sin(4x)\,dx,\) utilizando integración por partes
6)\(\displaystyle ∫\frac{1}{x^2\sqrt{x^2+16}}\,dx,\) mediante sustitución trigonométrica
- Contestar
- \(\displaystyle ∫\frac{1}{x^2\sqrt{x^2+16}}\,dx = −\frac{\sqrt{x^2+16}}{16x}+C\)
7)\(\displaystyle ∫\sqrt{x}\ln x\,dx,\) utilizando integración por partes
8)\(\displaystyle ∫\frac{3x}{x^3+2x^2−5x−6}\,dx,\) usando fracciones parciales
- Contestar
- \(\displaystyle ∫\frac{3x}{x^3+2x^2−5x−6}\,dx = \frac{1}{10}\big(4\ln|2−x|+5\ln|x+1|−9\ln|x+3|\big)+C\)
9)\(\displaystyle ∫\frac{x^5}{(4x^2+4)^{5/2}}\,dx,\) mediante sustitución trigonométrica
10)\(\displaystyle ∫\frac{\sqrt{4−\sin^2(x)}}{\sin^2(x)}\cos(x)\,dx,\) usando una tabla de integrales o un CAS
- Contestar
- \(\displaystyle ∫\frac{\sqrt{4−\sin^2(x)}}{\sin^2(x)}\cos(x)\,dx = −\frac{\sqrt{4−\sin^2(x)}}{\sin(x)}−\frac{x}{2}+C\)
En los ejercicios 11 - 15, integre usando cualquier método que elija.
11)\(\displaystyle ∫\sin^2 x\cos^2 x\,dx\)
12)\(\displaystyle ∫x^3\sqrt{x^2+2}\,dx\)
- Contestar
- \(\displaystyle ∫x^3\sqrt{x^2+2}\,dx = \frac{1}{15}(x^2+2)^{3/2}(3x^2−4)+C\)
13)\(\displaystyle ∫\frac{3x^2+1}{x^4−2x^3−x^2+2x}\,dx\)
14)\(\displaystyle ∫\frac{1}{x^4+4}\,dx\)
- Contestar
- \(\displaystyle ∫\frac{1}{x^4+4}\,dx = \frac{1}{16}\ln(\frac{x^2+2x+2}{x^2−2x+2})−\frac{1}{8}\tan^{−1}(1−x)+\frac{1}{8}\tan^{−1}(x+1)+C\)
15)\(\displaystyle ∫\frac{\sqrt{3+16x^4}}{x^4}\,dx\)
En los ejercicios 16 - 18, aproxime las integrales usando la regla del punto medio, la regla trapezoidal y la regla de Simpson usando cuatro subintervalos, redondeando a tres decimales.
16) [T]\(\displaystyle ∫^2_1\sqrt{x^5+2}\,dx\)
- Contestar
- \(M_4=3.312,\)
\(T_4=3.354,\)
\(S_4=3.326\)
17) [T]\(\displaystyle ∫^{\sqrt{π}}_0e^{−\sin(x^2)}\,dx\)
18) [T]\(\displaystyle ∫^4_1\frac{\ln(1/x)}{x}\,dx\)
- Contestar
- \(M_4=−0.982,\)
\(T_4=−0.917,\)
\(S_4=−0.952\)
En los ejercicios 19 - 20, evaluar las integrales, si es posible.
19) ¿\(\displaystyle ∫^∞_1\frac{1}{x^n}\,dx,\)para qué valores de\(n\) esta integral converge o diverge?
20)\(\displaystyle ∫^∞_1\frac{e^{−x}}{x}\,dx\)
- Contestar
- aproximadamente 0.2194
En los ejercicios 21 - 22, considere la función gamma dada por\(\displaystyle Γ(a)=∫^∞_0e^{−y}y^{a−1}\,dy.\)
21) Demostrar que\(\displaystyle Γ(a)=(a−1)Γ(a−1).\)
22) Extender para mostrar que\(\displaystyle Γ(a)=(a−1)!,\) asumir\(a\) es un entero positivo.
El auto más rápido del mundo, el Bugati Veyron, puede alcanzar una velocidad máxima de 408 km/h La gráfica representa su velocidad.
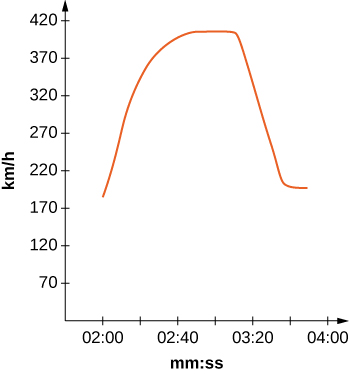
23) [T] Utilice la gráfica para estimar la velocidad cada 20 segundos y ajustar a una gráfica de la forma\(v(t)=ae^{bx}\sin(cx)+d.\) (Pista: Considere las unidades de tiempo.)
24) [T] Usando su función del problema anterior, encuentre exactamente hasta dónde viajó el Bugati Veyron en los 1 min 40 seg incluidos en la gráfica.
- Contestar
- Las respuestas pueden variar. Ej.:\(9.405\) km