8.4: La Ecuación Logística
- Page ID
- 116239
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Describir el concepto de capacidad de carga ambiental en el modelo logístico de crecimiento poblacional.
- Dibuja un campo de dirección para una ecuación logística e interpreta las curvas de solución.
- Resolver una ecuación logística e interpretar los resultados.
Las ecuaciones diferenciales se pueden utilizar para representar el tamaño de una población, ya que varía con el tiempo. Esto lo vimos en un capítulo anterior de la sección sobre crecimiento exponencial y decaimiento, que es el modelo más simple. Un modelo más realista incluye otros factores que afectan el crecimiento de la población. En esta sección, estudiamos la ecuación diferencial logística y vemos cómo se aplica al estudio de la dinámica poblacional en el contexto de la biología.
Crecimiento poblacional y capacidad de carga
Para modelar el crecimiento poblacional usando una ecuación diferencial, primero necesitamos introducir algunas variables y términos relevantes. La variable\(t\). representará el tiempo. Las unidades de tiempo pueden ser horas, días, semanas, meses o incluso años. Cualquier problema dado debe especificar las unidades utilizadas en ese problema en particular. La variable\(P\) representará población. Dado que la población varía con el tiempo, se entiende que es una función del tiempo. Por lo tanto, utilizamos la notación\(P(t)\) para la población en función del tiempo. Si\(P(t)\) es una función diferenciable, entonces la primera derivada\(\frac{dP}{dt}\) representa la tasa instantánea de cambio de la población en función del tiempo.
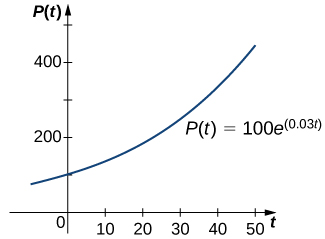
En Crecimiento Exponencial y Decaimiento, se estudió el crecimiento exponencial y desintegración de poblaciones y sustancias radiactivas. Un ejemplo de una función de crecimiento exponencial es\(P(t)=P_0e^{rt}.\) En esta función,\(P(t)\) representa la población en el momento\(t,P_0\) representa la población inicial (población en el momento\(t=0\)), y la constante\(r>0\) se denomina tasa de crecimiento. La figura\(\PageIndex{1}\) muestra una gráfica de\(P(t)=100e^{0.03t}\). Aquí\(P_0=100\) y\(r=0.03\).
Podemos verificar que la función\(P(t)=P_0e^{rt}\) satisface el problema del valor inicial
\[ \dfrac{dP}{dt}=rP \nonumber \]
con\(P(0)=P_0.\)
Esta ecuación diferencial tiene una interpretación interesante. El lado izquierdo representa la tasa a la que la población aumenta (o disminuye). El lado derecho es igual a una constante positiva multiplicada por la población actual. Por lo tanto, la ecuación diferencial establece que la tasa a la que aumenta la población es proporcional a la población en ese momento. Además, afirma que la constante de proporcionalidad nunca cambia.
Un problema con esta función es su predicción de que a medida que pasa el tiempo, la población crece sin ataduras. Esto no es realista en un entorno del mundo real. Diversos factores limitan la tasa de crecimiento de una población en particular, incluyendo la tasa de natalidad, tasa de mortalidad, suministro de alimentos, depredadores, etc. La constante de crecimiento\(r\) suele tomar en consideración las tasas de nacimiento y mortalidad pero ninguno de los otros factores, y puede interpretarse como una tasa de crecimiento porcentual neta (nacimiento menos muerte) por unidad de tiempo. Una pregunta natural es si la tasa de crecimiento poblacional se mantiene constante, o si cambia con el tiempo. Los biólogos han encontrado que en muchos sistemas biológicos, la población crece hasta llegar a cierta población en estado estacionario. Esta posibilidad no se toma en cuenta con el crecimiento exponencial. Sin embargo, el concepto de capacidad de carga permite la posibilidad de que en un área determinada, solo un cierto número de un organismo o animal dado pueda prosperar sin toparse con problemas de recursos.
La capacidad de carga de un organismo en un ambiente dado se define como la población máxima de ese organismo que el ambiente pueda sostener indefinidamente.
Utilizamos la variable\(K\) para denotar la capacidad de carga. La tasa de crecimiento está representada por la variable\(r\). Usando estas variables, podemos definir la ecuación diferencial logística.
Dejar\(K\) representar la capacidad de carga de un organismo en particular en un ambiente dado, y dejar que\(r\) sea un número real que represente la tasa de crecimiento. La función\(P(t)\) representa la población de este organismo en función del tiempo\(t\), y la constante\(P_0\) representa la población inicial (población del organismo en el momento\(t=0\)). Entonces la ecuación diferencial logística es
\[\dfrac{dP}{dt}=rP\left(1−\dfrac{P}{K}\right). \label{LogisticDiffEq} \]
La ecuación logística fue publicada por primera vez por Pierre Verhulst en\(1845\). Esta ecuación diferencial se puede acoplar con la condición inicial\(P(0)=P_0\) para formar un problema de valor inicial para\(P(t).\)
Supongamos que la población inicial es pequeña en relación con la capacidad de carga. Entonces\(\frac{P}{K}\) es pequeño, posiblemente cercano a cero. Así, la cantidad entre paréntesis en el lado derecho de la ecuación\ ref {logisticDiffeq} está cerca de\(1\), y el lado derecho de esta ecuación está cerca de\(rP\). Si\(r>0\), entonces la población crece rápidamente, pareciéndose al crecimiento exponencial.
Sin embargo, a medida que la población crece, la proporción\(\frac{P}{K}\) también crece, porque\(K\) es constante. Si la población permanece por debajo de la capacidad de carga, entonces\(\frac{P}{K}\) es menor que\(1\), entonces\(1−\frac{P}{K}>0\). Por lo tanto, el lado derecho de la Ecuación\ ref {LogisticDiFFEQ} sigue siendo positivo, pero la cantidad entre paréntesis se hace más pequeña, y la tasa de crecimiento disminuye como resultado. Si\(P=K\) entonces el lado derecho es igual a cero, y la población no cambia.
Ahora supongamos que la población inicia en un valor superior a la capacidad de carga. Entonces\(\frac{P}{K}>1,\) y\(1−\frac{P}{K}<0\). Entonces el lado derecho de la Ecuación\ ref {LogisticDiFFEQ} es negativo, y la población disminuye. Siempre y cuando\(P>K\), la población disminuya. En realidad nunca llega a K porque\(\frac{dP}{dt}\) se hará cada vez más pequeño, pero la población se acerca a la capacidad de carga a medida que se\(t\) acerca al infinito. Este análisis se puede representar visualmente a través de una línea de fase. Una línea de fase describe el comportamiento general de una solución a una ecuación diferencial autónoma, dependiendo de la condición inicial. Para el caso de una capacidad de carga en la ecuación logística, la línea de fase es como se muestra en la Figura\(\PageIndex{2}\).
Esta línea de fase muestra que cuando\(P\) es menor que cero o mayor que\(K\), la población disminuye con el tiempo. Cuando\(P\) está entre\(0\) y\(K\), la población aumenta con el tiempo.
Consideremos la población de venado cola blanca (Odocoileus virginianus) en el estado de Kentucky. El Departamento de Recursos de Pesca y Vida Silvestre de Kentucky (KDFWR) establece pautas para la caza y la pesca en el estado. Antes de la temporada de caza de 2004, se estimó una población de 900 mil venados. Johnson señala: “Una población de ciervos que tiene mucho para comer y que no es cazada por humanos u otros depredadores se duplicará cada tres años”. (George Johnson, “El problema de la explosión de las poblaciones de ciervos no tiene soluciones atractivas”, 12 de enero de 2001, consultado el 9 de abril de 2015)

Esta observación corresponde a una tasa de incremento\(r=\dfrac{\ln (2)}{3}=0.2311,\) por lo que la tasa de crecimiento aproximada es de 23.11% anual. (Esto supone que la población crece exponencialmente, lo cual es razonable —al menos en el corto plazo— con abundante suministro de alimentos y sin depredadores). El KDFWR también reporta densidades de población de ciervos para 32 condados en Kentucky, cuyo promedio es de aproximadamente 27 venados por milla cuadrada. Supongamos que esta es la densidad de venados para todo el estado (39,732 millas cuadradas). La capacidad de carga\(K\) es de 39,732 millas cuadradas por 27 venados por milla cuadrada, o 1,072,764 ciervos.
- Para esta aplicación, tenemos\(P_0=900,000,K=1,072,764,\) y\(r=0.2311.\) sustituimos estos valores en Ecuación\ ref {LogisticDiffeq} y formamos el problema del valor inicial.
- Resolver el problema del valor inicial de la parte a.
- Según este modelo, ¿cuál será la población en\(3\) años? Recordemos que el tiempo de duplicación predicho por Johnson para la población de ciervos fue de\(3\) años. ¿Cómo se comparan estos valores?
Supongamos que la población logró llegar a 1,200,000 ¿Qué predice la ecuación logística le pasará a la población en este escenario?
Solución
a. El problema de valor inicial es
\[ \dfrac{dP}{dt}=0.2311P \left(1−\dfrac{P}{1,072,764}\right),\,\,P(0)=900,000. \nonumber \]
b. La ecuación logística es una ecuación diferencial autónoma, por lo que podemos utilizar el método de separación de variables.
Paso 1: Establecer el lado derecho igual a cero da\(P=0\) y\(P=1,072,764.\) Esto significa que si la población comienza en cero nunca cambiará, y si comienza en la capacidad de carga, nunca cambiará.
Paso 2: Reescribe la ecuación diferencial y multiplica ambos lados por:
\[ \begin{align*} \dfrac{dP}{dt} =0.2311P\left(\dfrac{1,072,764−P}{1,072,764} \right) \\[4pt] dP =0.2311P\left(\dfrac{1,072,764−P}{1,072,764}\right)dt \\[4pt] \dfrac{dP}{P(1,072,764−P)} =\dfrac{0.2311}{1,072,764}dt. \end{align*}\]
Paso 3: Integrar ambos lados de la ecuación usando descomposición parcial de la fracción:
\[ \begin{align*} ∫\dfrac{dP}{P(1,072,764−P)} =∫\dfrac{0.2311}{1,072,764}dt \\[4pt] \dfrac{1}{1,072,764}∫ \left(\dfrac{1}{P}+\dfrac{1}{1,072,764−P}\right)dP =\dfrac{0.2311t}{1,072,764}+C \\[4pt] \dfrac{1}{1,072,764}\left(\ln |P|−\ln |1,072,764−P|\right) =\dfrac{0.2311t}{1,072,764}+C. \end{align*} \nonumber \]
Paso 4: Multiplica ambos lados por 1,072,764 y usa la regla del cociente para logaritmos:
\[\ln \left|\dfrac{P}{1,072,764−P}\right|=0.2311t+C_1. \nonumber \]
Aquí\(C_1=1,072,764C.\) Siguiente exponenciar ambos lados y eliminar el valor absoluto:
\[ \begin{align*} e^{\ln \left|\dfrac{P}{1,072,764−P} \right|} =e^{0.2311t + C_1} \\[4pt] \left|\dfrac{P}{1,072,764 - P}\right| =C_2e^{0.2311t} \\[4pt] \dfrac{P}{1,072,764−P} =C_2e^{0.2311t}. \end{align*}\]
Aquí\(C_2=e^{C_1}\) pero después de eliminar el valor absoluto, también puede ser negativo. Ahora resuelve para:
\[ \begin{align*} P =C_2e^{0.2311t}(1,072,764−P) \\[4pt] P =1,072,764C_2e^{0.2311t}−C_2Pe^{0.2311t} \\[4pt] P + C_2Pe^{0.2311t} = 1,072,764C_2e^{0.2311t} \\[4pt] P(1+C_2e^{0.2311t} =1,072,764C_2e^{0.2311t} \\[4pt] P(t) =\dfrac{1,072,764C_2e^{0.2311t}}{1+C_2e^{0.23\nonumber11t}}. \end{align*}\]
Paso 5: Para determinar el valor de\(C_2\), en realidad es más fácil retroceder un par de pasos a donde\(C_2\) se definió. En particular, utilice la ecuación
\[\dfrac{P}{1,072,764−P}=C_2e^{0.2311t}. \nonumber \]
La condición inicial es\(P(0)=900,000\). Reemplazar\(P\) con\(900,000\) y\(t\) con cero:
\[ \begin{align*} \dfrac{P}{1,072,764−P} =C_2e^{0.2311t} \\[4pt] \dfrac{900,000}{1,072,764−900,000} =C_2e^{0.2311(0)} \\[4pt] \dfrac{900,000}{172,764} =C_2 \\[4pt] C_2 =\dfrac{25,000}{4,799} \\[4pt] ≈5.209. \end{align*}\]
Por lo tanto
\[ \begin{align*} P(t) =\dfrac{1,072,764 \left(\dfrac{25000}{4799}\right)e^{0.2311t}}{1+(250004799)e^{0.2311t}}\\[4pt] =\dfrac{1,072,764(25000)e^{0.2311t}}{4799+25000e^{0.2311t}.} \end{align*}\]
Dividiendo el numerador y denominador entre 25.000 da
\[P(t)=\dfrac{1,072,764e^{0.2311t}}{0.19196+e^{0.2311t}}. \nonumber \]
La figura es una gráfica de esta ecuación.
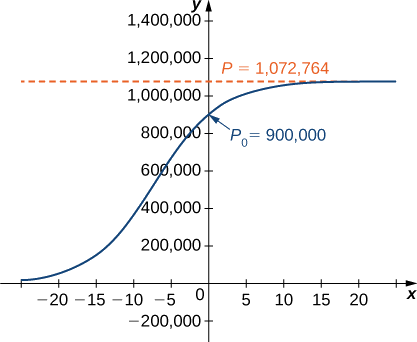
c. Utilizando este modelo podemos predecir la población en 3 años.
\[P(3)=\dfrac{1,072,764e^{0.2311(3)}}{0.19196+e^{0.2311(3)}}≈978,830\,deer \nonumber \]
Esto es muy inferior al doble de la población inicial de\(900,000.\) Recuerde que el tiempo de duplicación se basa en el supuesto de que la tasa de crecimiento nunca cambia, pero el modelo logístico toma en cuenta esta posibilidad.
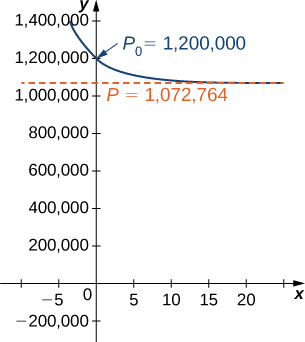
d. Si la población llegase a 1,200,000 venados, entonces el nuevo problema del valor inicial sería
\[ \dfrac{dP}{dt}=0.2311P \left(1−\dfrac{P}{1,072,764}\right), \, P(0)=1,200,000. \nonumber \]
La solución general a la ecuación diferencial seguiría siendo la misma.
\[ P(t)=\dfrac{1,072,764C_2e^{0.2311t}}{1+C_2e^{0.2311t}} \nonumber \]
Para determinar el valor de la constante, volver a la ecuación
\[ \dfrac{P}{1,072,764−P}=C_2e^{0.2311t}. \nonumber \]
Sustituyendo los valores\(t=0\) y\(P=1,200,000,\) obtienes
\[ \begin{align*} C_2e^{0.2311(0)} =\dfrac{1,200,000}{1,072,764−1,200,000} \\[4pt] C_2 =−\dfrac{100,000}{10,603}≈−9.431.\end{align*}\]
Por lo tanto
\[ \begin{align*} P(t) =\dfrac{1,072,764C_2e^{0.2311t}}{1+C_2e^{0.2311t}} \\[4pt] =\dfrac{1,072,764 \left(−\dfrac{100,000}{10,603}\right)e^{0.2311t}}{1+\left(−\dfrac{100,000}{10,603}\right)e^{0.2311t}} \\[4pt] =−\dfrac{107,276,400,000e^{0.2311t}}{100,000e^{0.2311t}−10,603} \\[4pt] ≈\dfrac{10,117,551e^{0.2311t}}{9.43129e^{0.2311t}−1} \end{align*}\]
Esta ecuación se grafica en la Figura\(\PageIndex{5}\).
Resolviendo la Ecuación Diferencial Logística
La ecuación diferencial logística es una ecuación diferencial autónoma, por lo que podemos usar la separación de variables para encontrar la solución general, como acabamos de hacer en Ejemplo\(\PageIndex{1}\).
Paso 1: Establecer el lado derecho igual a cero conduce a\(P=0\) y\(P=K\) como soluciones constantes. La primera solución indica que cuando no hay organismos presentes, la población nunca crecerá. La segunda solución indica que cuando la población inicia en la capacidad de carga, nunca cambiará.
Paso 2: Reescribir la ecuación diferencial en la forma
\[ \dfrac{dP}{dt}=\dfrac{rP(K−P)}{K}. \nonumber \]
Luego multiplica ambos lados por\(dt\) y divide ambos lados por\(P(K−P).\) Esto lleva a
\[ \dfrac{dP}{P(K−P)}=\dfrac{r}{K}dt. \nonumber \]
Multiplica ambos lados de la ecuación por\(K\) e integra:
\[ ∫\dfrac{K}{P(K−P)}dP=∫rdt. \label{eq20a} \]
El lado izquierdo de esta ecuación se puede integrar utilizando la descomposición parcial de la fracción. Te dejamos que verifiques que
\[ \dfrac{K}{P(K−P)}=\dfrac{1}{P}+\dfrac{1}{K−P}. \nonumber \]
Entonces la Ecuación\ ref {eq20a} se convierte
\[ ∫\dfrac{1}{P}+\dfrac{1}{K−P}dP=∫rdt \nonumber \]
\[ \ln |P|−\ln |K−P|=rt+C \nonumber \]
\[ \ln ∣\dfrac{P}{K−P}∣=rt+C. \nonumber \]
Ahora exponenciar ambos lados de la ecuación para eliminar el logaritmo natural:
\[ e^{\ln ∣\dfrac{P}{K−P}∣}=e^{rt+C} \nonumber \]
\[ ∣\dfrac{P}{K−P}∣=e^Ce^{rt}. \nonumber \]
Definimos\(C_1=e^c\) para que la ecuación se convierta
\[ \dfrac{P}{K−P}=C_1e^{rt}. \label{eq30a} \]
Para resolver esta ecuación para\(P(t)\), primero multiplique ambos lados por\(K−P\) y recoja los términos que contienen\(P\) en el lado izquierdo de la ecuación:
\[\begin{align*} P =C_1e^{rt}(K−P) \\[4pt] =C_1Ke^{rt}−C_1Pe^{rt} \\[4pt] P+C_1Pe^{rt} =C_1Ke^{rt}.\end{align*}\]
A continuación, factorizar\(P\) desde el lado izquierdo y dividir ambos lados por el otro factor:
\[\begin{align*} P(1+C_1e^{rt}) =C_1Ke^{rt} \\[4pt] P(t) =\dfrac{C_1Ke^{rt}}{1+C_1e^{rt}}. \end{align*}\]
El último paso es determinar el valor de\(C_1.\) La forma más fácil de hacerlo es sustituyendo\(t=0\) y\(P_0\) en lugar de\(P\) en Ecuación y resolver por\(C_1\):
\[\begin{align*} \dfrac{P}{K−P} = C_1e^{rt} \\[4pt] \dfrac{P_0}{K−P_0} =C_1e^{r(0)} \\[4pt] C_1 = \dfrac{P_0}{K−P_0}. \end{align*}\]
Finalmente, sustituya la expresión por\(C_1\) en Ecuación\ ref {eq30a}:
\[ P(t)=\dfrac{C_1Ke^{rt}}{1+C_1e^{rt}}=\dfrac{\dfrac{P_0}{K−P_0}Ke^{rt}}{1+\dfrac{P_0}{K−P_0}e^{rt}} \nonumber \]
Ahora multiplica el numerador y denominador del lado derecho por\((K−P_0)\) y simplifica:
\[\begin{align*} P(t) =\dfrac{\dfrac{P_0}{K−P_0}Ke^{rt}}{1+\dfrac{P_0}{K−P_0}e^{rt}} \\[4pt] =\dfrac{\dfrac{P_0}{K−P_0}Ke^{rt}}{1+\dfrac{P_0}{K−P_0}e^{rt}}⋅\dfrac{K−P_0}{K−P_0} =\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}}. \end{align*}\]
Declaramos este resultado como teorema.
Considerar la ecuación diferencial logística sujeta a una población inicial de\(P_0\) con capacidad de carga\(K\) y tasa de crecimiento\(r\). La solución al problema del valor inicial correspondiente viene dada por
\[P(t)=\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}} \nonumber \].
Ahora que tenemos la solución al problema del valor inicial, podemos elegir valores para\(P_0,r\),\(K\) y estudiar la curva de solución. Por ejemplo, en Ejemplo se utilizaron los valores\(r=0.2311,K=1,072,764,\) y una población inicial de\(900,000\) ciervos. Esto lleva a la solución
\[\begin{align*} P(t) =\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}}\\[4pt] =\dfrac{900,000(1,072,764)e^{0.2311t}}{(1,072,764−900,000)+900,000e^{0.2311t}}\\[4pt] =\dfrac{900,000(1,072,764)e^{0.2311t}}{172,764+900,000e^{0.2311t}}.\end{align*}\]
Dividiendo la parte superior e inferior por\(900,000\) da
\[ P(t)=\dfrac{1,072,764e^{0.2311t}}{0.19196+e^{0.2311t}}. \nonumber \]
Esto es lo mismo que la solución original. La gráfica de esta solución se muestra nuevamente en azul en la Figura\(\PageIndex{6}\), superpuesta sobre la gráfica del modelo de crecimiento exponencial con población inicial\(900,000\) y tasa de crecimiento\(0.2311\) (apareciendo en verde). La línea discontinua roja representa la capacidad de carga, y es una asíntota horizontal para la solución a la ecuación logística.
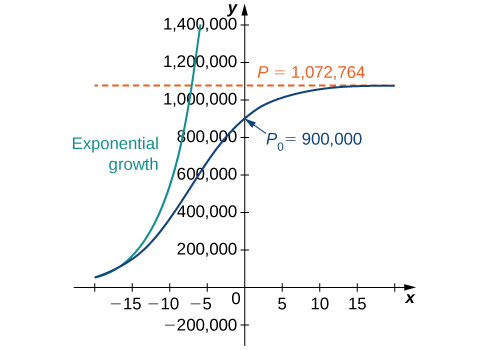
Trabajando bajo el supuesto de que la población crece de acuerdo con la ecuación diferencial logística, esta gráfica predice que aproximadamente\(20\) años antes\((1984)\), el crecimiento de la población estuvo muy cerca de exponencial. La tasa de crecimiento neto en ese momento habría sido de alrededor\(23.1%\) por año. A medida que pasa el tiempo, las dos gráficas se separan. Esto sucede porque la población aumenta, y la ecuación diferencial logística establece que la tasa de crecimiento disminuye a medida que aumenta la población. En el momento en que se midió la población\((2004)\), estaba cerca de la capacidad de carga, y la población comenzaba a nivelarse.
La solución a la ecuación diferencial logística tiene un punto de inflexión. Para encontrar este punto, establezca la segunda derivada igual a cero:
\[ \begin{align*} P(t) =\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}} \\[4pt] P′(t) =\dfrac{rP_0K(K−P0)e^{rt}}{((K−P_0)+P_0e^{rt})^2} \\[4pt] P''(t) =\dfrac{r^2P_0K(K−P_0)^2e^{rt}−r^2P_0^2K(K−P_0)e^{2rt}}{((K−P_0)+P_0e^{rt})^3} \\[4pt] =\dfrac{r^2P_0K(K−P_0)e^{rt}((K−P_0)−P_0e^{rt})}{((K−P_0)+P_0e^{rt})^3}. \end{align*}\]
Establecer el numerador igual a cero,
\[ r^2P_0K(K−P_0)e^{rt}((K−P_0)−P_0e^{rt})=0. \nonumber \]
Siempre y cuando\(P_0≠K\), la cantidad total antes e incluyendo\(e^{rt}\) sea distinta de cero, así podemos dividirla:
\[ (K−P_0)−P_0e^{rt}=0. \nonumber \]
Resolviendo para\(t\),
\[ P_0e^{rt}=K−P_0 \nonumber \]
\[ e^{rt}=\dfrac{K−P_0}{P_0} \nonumber \]
\[ \ln e^{rt}=\ln \dfrac{K−P_0}{P_0} \nonumber \]
\[ rt=\ln \dfrac{K−P_0}{P_0} \nonumber \]
\[ t=\dfrac{1}{r}\ln \dfrac{K−P_0}{P_0}. \nonumber \]
Observe que si\(P_0>K\), entonces esta cantidad es indefinida, y la gráfica no tiene un punto de inflexión. En la gráfica logística, el punto de inflexión puede verse como el punto donde el gráfico cambia de cóncavo hacia abajo a cóncavo. Aquí es donde comienza a ocurrir la “nivelación”, debido a que la tasa de crecimiento neto se vuelve más lenta a medida que la población comienza a acercarse a la capacidad de carga.
Se observa que una población de conejos en un prado son\(200\) conejos a la vez\(t=0\). Después de un mes, se observa que la población de conejos ha aumentado en\(4%\). Utilizando una población inicial\(200\) y una tasa de crecimiento de\(0.04\), con capacidad de carga de\(750\) conejos,
- Escribir la ecuación diferencial logística y la condición inicial para este modelo.
- Dibujar un campo de pendiente para esta ecuación diferencial logística y esbozar la solución correspondiente a una población inicial de\(200\) conejos.
- Resolver el problema del valor inicial para\(P(t)\).
- Utilizar la solución para predecir la población tras\(1\) año.
- Pista
-
Primero determinar los valores de\(r,K,\) y\(P_0\). Luego cree el problema del valor inicial, dibuje el campo de dirección y resuelva el problema.
- Contestar
-
a.\(\dfrac{dP}{dt}=0.04(1−\dfrac{P}{750}),P(0)=200\)
b.
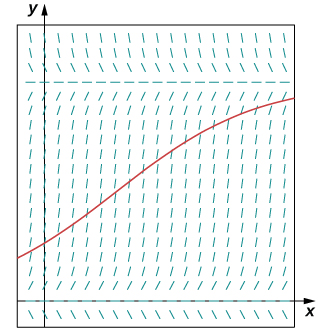
c.\(P(t)=\dfrac{3000e^{.04t}}{11+4e^{.04t}}\)
d. Después de\(12\) meses, la población será de\(P(12)≈278\) conejos.
Una mejora del modelo logístico incluye una población umbral. La población umbral se define como la población mínima necesaria para que la especie sobreviva. Utilizamos la variable\(T\) para representar la población umbral. Una ecuación diferencial que incorpora tanto la población umbral como\(T\) la capacidad de carga\(K\) es
\[ \dfrac{dP}{dt}=−rP\left(1−\dfrac{P}{K}\right)\left(1−\dfrac{P}{T}\right) \nonumber \]
donde\(r\) representa la tasa de crecimiento, como antes.
- La población umbral es útil para los biólogos y puede ser utilizada para determinar si una especie dada debe ser colocada en la lista en peligro de extinción. Un grupo de investigadores australianos dicen que han determinado el umbral de población para que sobreviva cualquier especie:\(5000\) los adultos. (Catherine Clabby, “Un número mágico”, científico estadounidense 98 (1): 24, doi:10.1511/2010.82.24. accessed abril 9, 2015, www.americanscientist.org/iss... a-magic-number). Por lo tanto\(T=5000\), utilizamos como población umbral en este proyecto. Supongamos que la capacidad de carga ambiental en Montana para alces es\(25,000\). Configurar Ecuación utilizando la capacidad de carga de\(25,000\) y población umbral de\(5000\). Asumir una tasa de crecimiento neto anual de 18%.
- Dibuje el campo de dirección para la ecuación diferencial a partir del paso\(1\), junto con varias soluciones para diferentes poblaciones iniciales. ¿Cuáles son las soluciones constantes de la ecuación diferencial? ¿A qué corresponden estas soluciones en el modelo poblacional original (es decir, en un contexto biológico)?
- ¿Cuál es la población limitante para cada población inicial que elegiste en paso\(2\)? (Pista: usa el campo de pendiente para ver qué sucede para varias poblaciones iniciales, es decir, busca las asíntotas horizontales de tus soluciones.)
- Esta ecuación se puede resolver utilizando el método de separación de variables. Sin embargo, es muy difícil obtener la solución como una función explícita de\(t\). Utilizando una población inicial de\(18,000\) alces, resolver el problema del valor inicial y expresar la solución como una función implícita de t, o resolver el problema general del valor inicial, encontrando una solución en términos de\(r,K,T,\) y\(P_0\).
Conceptos clave
- Al estudiar las funciones de la población, diferentes supuestos, como el crecimiento exponencial, el crecimiento logístico o la población umbral, conducen a diferentes tasas de crecimiento.
- La ecuación diferencial logística incorpora el concepto de capacidad de carga. Este valor es un valor limitante para la población para cualquier entorno dado.
- La ecuación diferencial logística se puede resolver para cualquier tasa de crecimiento positivo, población inicial y capacidad de carga.
Ecuaciones Clave
- Ecuación diferencial logística y problema de valor inicial
\(\dfrac{dP}{dt}=rP\left(1−\dfrac{P}{K}\right),\quad P(0)=P_0\)
- Solución al problema de ecualización diferencial logístico/valor inicial
\(P(t)=\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}}\)
- Modelo de población umbral
\(\dfrac{dP}{dt}=−rP\left(1−\dfrac{P}{K}\right)\left(1−\dfrac{P}{T}\right)\)
Glosario
- capacidad de carga
- la población máxima de un organismo que el medio ambiente puede sostener indefinidamente
- tasa de crecimiento
- la constante\(r>0\) en la función de crecimiento exponencial\(P(t)=P_0e^{rt}\)
- población inicial
- la población en el momento\(t=0\)
- ecuación diferencial logística
- una ecuación diferencial que incorpora la capacidad de carga\(K\) y la tasa de crecimiento rr en un modelo poblacional
- línea de fase
- una representación visual del comportamiento de las soluciones a una ecuación diferencial autónoma sujeta a diversas condiciones iniciales
- población umbral
- la población mínima necesaria para que una especie sobreviva


