10.4: Trabajar con la serie Taylor
- Page ID
- 116129
- Escribir los términos de la serie binomial.
- Reconocer las expansiones de funciones comunes de la serie Taylor.
- Reconocer y aplicar técnicas para encontrar la serie Taylor para una función.
- Utilice la serie Taylor para resolver ecuaciones diferenciales.
- Utilice la serie Taylor para evaluar integrales no elementales.
En la sección anterior, definimos series de Taylor y mostramos cómo encontrar la serie Taylor para varias funciones comunes calculando explícitamente los coeficientes de los polinomios de Taylor. En esta sección mostramos cómo usar esas series de Taylor para derivar series Taylor para otras funciones. A continuación presentamos dos aplicaciones comunes de la serie de potencia. Primero, mostramos cómo se pueden usar las series de potencia para resolver ecuaciones diferenciales. En segundo lugar, mostramos cómo las series de poder pueden ser utilizadas para evaluar integrales cuando la antiderivada de la integral no puede expresarse en términos de funciones elementales. En un ejemplo, consideramos\(\displaystyle \int e^{−x^2}dx,\) una integral que surge frecuentemente en la teoría de la probabilidad.
La serie binomial
Nuestro primer objetivo en esta sección es determinar la serie Maclaurin para la función\( f(x)=(1+x)^r\) para todos los números reales\( r\). La serie Maclaurin para esta función se conoce como la serie binomial. Comenzamos por considerar el caso más simple:\( r\) es un entero no negativo. Recordamos que, pues se\( r=0,\,1,\,2,\,3,\,4,\;f(x)=(1+x)^r\) puede escribir como
\[\begin{align*} f(x) &=(1+x)^0=1, \\[4pt] f(x) &=(1+x)^1=1+x, \\[4pt] f(x) &=(1+x)^2=1+2x+x^2, \\[4pt] f(x) &=(1+x)^3=1+3x+3x^2+x^3 \\[4pt] f(x) &=(1+x)^4=1+4x+6x^2+4x^3+x^4. \end{align*}\]
Las expresiones del lado derecho se conocen como expansiones binomiales y los coeficientes se conocen como coeficientes binomiales. Más generalmente, para cualquier entero no negativo\( r\), el coeficiente binomial de\( x^n\) en la expansión binomial de\( (1+x)^r\) viene dado por
\[\binom{r}{n}=\dfrac{r!}{n!(r−n)!}\label{eq6.6} \]
y
\ [\ begin {align} f (x) &= (1+x) ^r\ nonumber\\ [5pt]
&=\ binom {r} {0} +\ binom {r} {1} x+\ binom {r} {2} x^2+\ binom {r} {3} x^3++\ binom {r} {r-1} x^ {r−1} +\ binom {r} {r} x^r\ nonumber\\ [5pt]
&=\ suma_ {n=0} ^r\ binom {r} {n} x^n.\ etiqueta {eq6.7}\ end {align}\]
Por ejemplo, usando esta fórmula para\( r=5\), vemos que
\[ \begin{align*} f(x) &=(1+x)^5 \\[4pt] &=\binom{5}{0}1+\binom{5}{1}x+\binom{5}{2}x^2+\binom{5}{3}x^3+\binom{5}{4}x^4+\binom{5}{5}x^5 \\[4pt] &=\dfrac{5!}{0!5!}1+\dfrac{5!}{1!4!}x+\dfrac{5!}{2!3!}x^2+\dfrac{5!}{3!2!}x^3+\dfrac{5!}{4!1!}x^4+\dfrac{5!}{5!0!}x^5 \\[4pt] &=1+5x+10x^2+10x^3+5x^4+x^5. \end{align*}\]
Consideramos ahora el caso cuando el exponente\(r.\)
es cualquier número real, no necesariamente un entero no negativo. Si no\(r\) es un entero no negativo, entonces\(f(x)=(1+x)^r\) no se puede escribir como un polinomio finito. Sin embargo, podemos encontrar una serie de potencia para\(f\). Específicamente, buscamos la serie Maclaurin para\(f\). Para ello, encontramos los derivados de\(f\) y los evaluamos en\(x=0\).
\[ \begin{align*} f(x) &=(1+x)^r & f(0) &=1 \\[4pt] f′(x) &=r(1+x)^{r−1} & f'(0) &=r \\[4pt] f''(x) &=r(r−1)(1+x)^{r−2} & f''(0) &=r(r−1) \\[4pt] f'''(x) &=r(r−1)(r−2)(1+x)^{r−3} & f'''(0) &=r(r−1)(r−2) \\[4pt] f^{(n)}(x) &=r(r−1)(r−2)⋯(r−n+1)(1+x)^{r−n} & f^{(n)}(0) &=r(r−1)(r−2)⋯(r−n+1) \end{align*}\]
Concluimos que los coeficientes en la serie binomial están dados por
\[\dfrac{f^{(n)}(0)}{n!}=\dfrac{r(r−1)(r−2)⋯(r−n+1)}{n!}.\label{eq6.8} \]
Observamos que si\(r\) es un entero no negativo, entonces la\((r+1)^{\text{st}}\) derivada\( f^{(r+1)}\) es la función cero, y la serie termina. Además, si\( r\) es un entero no negativo, entonces la Ecuación\ ref {eq6.8} para los coeficientes concuerda con la Ecuación\ ref {eq6.6} para los coeficientes, y la fórmula para la serie binomial concuerda con la Ecuación\ ref {eq6.7} para la expansión binomial finita. De manera más general, para denotar los coeficientes binomiales para cualquier número real\( r\), definimos
\[\binom{r}{n}=\dfrac{(r−1)(r−2)⋯(r−n+1)}{n!}. \nonumber \]
Con esta notación, podemos escribir la serie binomial para\( (1+x)^r\) como
\[\sum_{n=0}^∞\binom{r}{n}x^n=1+rx+\dfrac{r(r−1)}{2!}x^2+⋯+\dfrac{r(r−1)⋯(r−n+1)}{n!}x^n+⋯. \label{bin1} \]
Ahora necesitamos determinar el intervalo de convergencia para la serie binomial Ecuación\ ref {bin1}. Aplicamos la prueba de ratio. En consecuencia, consideramos
\[\begin{align*} \dfrac{|a_{n+1}|}{|a_n|} &=\dfrac{|r(r−1)(r−2)⋯(r−n)|x||^{n+1}}{(n+1)!}⋅\dfrac{n}{|r(r−1)(r−2)⋯(r−n+1)||x|^n} \\[4pt] &=\dfrac{|r−n||x|}{|n+1|} \end{align*}\].
Desde
\[\lim_{n→∞}\dfrac{|a_{n+1}|}{|a_n|}=|x|<1 \nonumber \]
si y sólo si\( |x|<1\), concluimos que el intervalo de convergencia para la serie binomial es\( (−1,1)\). El comportamiento en los puntos finales depende de\( r\). Se puede demostrar que para\( r≥0\) la serie converge en ambos puntos finales; para\( −1<r<0\), la serie converge en\( x=1\) y diverge en\( x=−1\); y para\( r<−1\), la serie diverge en ambos extremos. La serie binomial sí converge a\( (1+x)^r\) in\( (−1,1)\) para todos los números reales\( r\), pero demostrando este hecho mostrando que el resto\( R_n(x)→0\) es difícil.
Para cualquier número real\( r\), la serie Maclaurin para\( f(x)=(1+x)^r\) es la serie binomial. Converge a\( f\) for\( |x|<1\), y escribimos
\[(1+x)^r=\sum_{n=0}^∞\binom{r}{n}x^n=1+rx+\dfrac{r(r−1)}{2!}x^2+⋯+r\dfrac{(r−1)⋯(r−n+1)}{n!}x^n+⋯ \nonumber \]
para\( |x|<1\).
Podemos usar esta definición para encontrar la serie binomial para\( f(x)=\sqrt{1+x}\) y usar la serie para aproximar\( \sqrt{1.5}\).
- Encuentra la serie binomial para\( f(x)=\sqrt{1+x}\).
- Utilice el polinomio Maclaurin de tercer orden\( p_3(x)\) para estimar\( \sqrt{1.5}\). Usa el teorema de Taylor para encuadernar el error. Utilice una utilidad gráfica para comparar las gráficas de\( f\) y\( p_3\).
Solución
a. aquí\( r=\dfrac{1}{2}\). Usando la definición para la serie binomial, obtenemos
\ (\ displaystyle\ qquad\ begin {align*}\ sqrt {1+x} &=1+\ dfrac {1} {2} x+\ dfrac {(1/2) (−1/2)} {2!} x^2+\ dfrac {(1/2) (−1/2) (−3/2)} {3!} x^3+\\ [5pt]
&=1+\ dfrac {1} {2} x−\ dfrac {1} {2!} \ dfrac {1} {2^2} x^2+\ dfrac {1} {3!} \ dfrac {13} {2^3} x^3−+\ dfrac {(−1) ^ {n+1}} {n!} \ dfrac {135( 2n−3)} {2^n} x^n+\\ [5pt]
&=1+\ suma_ {n=1} ^∞\ dfrac {(−1) ^ {n+1}} {n!} \ dfrac {135( 2n−3)} {2^n} x^n.\ end {alinear*}\)
b. del resultado en la parte a. el polinomio de Maclaurin de tercer orden es
\( p_3(x)=1+\dfrac{1}{2}x−\dfrac{1}{8}x^2+\dfrac{1}{16}x^3\).
Por lo tanto,
\( \sqrt{1.5}=\sqrt{1+0.5}≈1+\dfrac{1}{2}(0.5)−\dfrac{1}{8}(0.5)^2+\dfrac{1}{16}(0.5)^3≈1.2266.\)
Del teorema de Taylor, el error satisface
\( R_3(0.5)=\dfrac{f^{(4)}(c)}{4!}(0.5)^4\)
para algunos\( c\) entre\( 0\) y\( 0.5\). Ya que\( f^{(4)}(x)=−\dfrac{15}{2^4(1+x)^{7/2}}\), y el valor máximo de\( ∣f^{(4)}(x)∣\) en el intervalo\( (0,0.5)\) ocurre en\( x=0\), tenemos
\( |R_3(0.5)|≤\dfrac{15}{4!2^4}(0.5)^4≈0.00244.\)
La función y el polinomio Maclaurin\( p_3\) se grafican en la Figura\(\PageIndex{1}\).
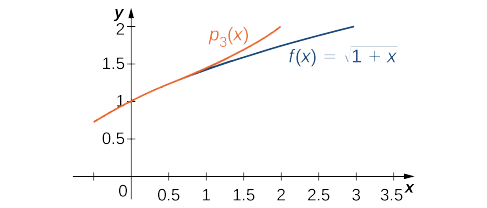
Encuentra la serie binomial para\( f(x)=\dfrac{1}{(1+x)^2}\).
- Pista
-
Utilice la definición de serie binomial para\( r=−2\).
- Responder
-
\(\displaystyle \sum_{n=0}^∞(−1)^n(n+1)x^n\)
Funciones comunes expresadas como serie Taylor
En este punto, hemos derivado series Maclaurin para funciones exponenciales, trigonométricas y logarítmicas, así como funciones de la forma\( f(x)=(1+x)^r\). En la Tabla\(\PageIndex{1}\), resumimos los resultados de estas series. Observamos que la convergencia de la serie Maclaurin para\( f(x)=\ln(1+x)\) en el punto final\( x=1\) y la serie Maclaurin para\( f(x)=\tan^{−1}x\) en los puntos finales\( x=1\) y\( x=−1\) se basa en un teorema más avanzado del que presentamos aquí. (Consulte el teorema de Abel para una discusión de este punto más técnico.)
| Función | Serie Maclaurin | Intervalo de Convergencia |
|---|---|---|
| \( f(x)=\dfrac{1}{1−x}\) | \(\displaystyle \sum_{n=0}^∞x^n\) | \( −1<x<1\) |
| \( f(x)=e^x\) | \(\displaystyle \sum_{n=0}^∞\dfrac{x^n}{n!}\) | \( −∞<x<∞\) |
| \( f(x)=\sin x\) | \(\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n+1}}{(2n+1)!}\) | \( −∞<x<∞\) |
| \( f(x)=\cos x\) | \(\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n}}{(2n)!}\) | \( −∞<x<∞\) |
| \( f(x)=\ln(1+x)\) | \(\displaystyle \sum_{n=0}^∞(−1)^{n+1}\dfrac{x^n}{n}\) | \( −1<x<1\) |
| \( f(x)=\tan^{−1}x\) | \(\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n+1}}{2n+1}\) | \( −1<x<1\) |
| \( f(x)=(1+x)^r\) | \(\displaystyle \sum_{n=0}^∞\binom{r}{n}x^n\) | \( −1<x<1\) |
Anteriormente en el capítulo, mostramos cómo se podían combinar series de potencia para crear nuevas series de potencia. Aquí utilizamos estas propiedades, combinadas con la serie Maclaurin en Table\(\PageIndex{1}\), para crear series Maclaurin para otras funciones.
Encuentre la serie Maclaurin de cada una de las siguientes funciones usando una de las series listadas en Tabla\(\PageIndex{1}\).
- \( f(x)=\cos\sqrt{x}\)
- \( f(x)=\sinh x\)
Solución
a. usando la serie Maclaurin para\( \cos x\) encontramos que la serie Maclaurin para\( \cos\sqrt{x}\) está dada por
\(\displaystyle \sum_{n=0}^∞\dfrac{(−1)^n(\sqrt{x})^{2n}}{(2n)!}=\sum_{n=0}^∞\dfrac{(−1)^nx^n}{(2n)!}=1−\dfrac{x}{2!}+\dfrac{x^2}{4!}−\dfrac{x^3}{6!}+\dfrac{x^4}{8!}−⋯.\)
Esta serie converge\( \cos\sqrt{x}\) para todos\( x\) en el dominio de\( \cos\sqrt{x}\); es decir, para todos\( x≥0\).
b. para encontrar la serie Maclaurin para\( \sinh x,\) nosotros utilizamos el hecho de que
\( \sinh x=\dfrac{e^x−e^{−x}}{2}.\)
Usando la serie Maclaurin para\( e^x\), vemos que el\(n^{\text{th}}\) término en la serie Maclaurin para\(\sinh x\) viene dado por
\( \dfrac{x^n}{n!}−\dfrac{(−x)^n}{n!}.\)
Para\( n\) par, este término es cero. Para\( n\) impar, este término es\( \dfrac{2x^n}{n!}\). Por lo tanto, la serie Maclaurin para solo\(\sinh x\) tiene términos de pedido impar y está dada por
\(\displaystyle \sum_{n=0}^∞\dfrac{x^{2n+1}}{(2n+1)!}=x+\dfrac{x^3}{3!}+\dfrac{x^5}{5!}+⋯.\)
Encuentra la serie Maclaurin para\( \sin(x^2).\)
- Pista
-
Utilice la serie Maclaurin para\( \sin x.\)
- Responder
-
\(\displaystyle \sum_{n=0}^∞\dfrac{(−1)^nx^{4n+2}}{(2n+1)!}\)
También mostramos anteriormente en este capítulo cómo las series de poder pueden diferenciarse término por término para crear una nueva serie de potencia. En Ejemplo\(\PageIndex{3}\), diferenciamos la serie binomial por\( \sqrt{1+x}\) término por término para encontrar la serie binomial para\( \dfrac{1}{\sqrt{1+x}}\). Tenga en cuenta que podríamos construir la serie binomial para\( \dfrac{1}{\sqrt{1+x}}\) directamente a partir de la definición, pero diferenciar la serie binomial para\( \sqrt{1+x}\) es un cálculo más fácil.
Utilice la serie binomial\( \sqrt{1+x}\) para encontrar la serie binomial para\( \dfrac{1}{\sqrt{1+x}}\).
Solución
Las dos funciones están relacionadas por
\( \dfrac{d}{dx}\sqrt{1+x}=\dfrac{1}{2\sqrt{1+x}}\),
por lo que la serie binomial para\( \dfrac{1}{\sqrt{1+x}}\) viene dada por
\(\displaystyle \dfrac{1}{\sqrt{1+x}}=2\dfrac{d}{dx}\sqrt{1+x}=1+\sum_{n=1}^∞\dfrac{(−1)^n}{n!}\dfrac{1⋅3⋅5⋯(2n−1)}{2^n}x^n.\)
Encuentra la serie binomial para\( f(x)=\dfrac{1}{(1+x)^{3/2}}\)
- Pista
-
Diferenciar la serie para\( \dfrac{1}{\sqrt{1+x}}\)
- Responder
-
\(\displaystyle \sum_{n=1}^∞\dfrac{(−1)^n}{n!}\dfrac{1⋅3⋅5⋯(2n−1)}{2^n}x^n\)
En este ejemplo, diferenciamos una serie conocida de Taylor para construir una serie Taylor para otra función. La capacidad de diferenciar series de potencia término por término las convierte en una poderosa herramienta para resolver ecuaciones diferenciales. Ahora mostramos cómo se logra esto.
Resolver ecuaciones diferenciales con series de potencia
Considerar la ecuación diferencial
\[y′(x)=y.\nonumber \]
Recordemos que esta es una ecuación separable de primer orden y su solución es\(y=Ce^x\). Esta ecuación se resuelve fácilmente utilizando técnicas discutidas anteriormente en el texto. Para la mayoría de las ecuaciones diferenciales, sin embargo, aún no contamos con herramientas analíticas para resolverlas. Las series Power son una herramienta extremadamente útil para resolver muchos tipos de ecuaciones diferenciales. En esta técnica, buscamos una solución de la forma\(\displaystyle y=\sum_{n=0}^∞c_nx^n\) y determinamos cuáles serían los coeficientes que necesitarían ser. En el siguiente ejemplo, consideramos un problema de valor inicial que implica\(y′=y\) ilustrar la técnica.
Utilice series de potencia para resolver el problema del valor inicial\(y′=y,\quad y(0)=3.\)
Solución
Supongamos que existe una solución de serie de potencia
\(\displaystyle y(x)=\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+c_3x^3+c_4x^4+⋯.\)
Diferenciando esta serie término por término, obtenemos
\( y′=c_1+2c_2x+3c_3x^2+4c_4x^3+⋯.\)
Si\(y\) satisface la ecuación diferencial, entonces
\( c_0+c_1x+c_2x^2+c_3x^3+⋯=c_1+2c_2x+3c_3x^2+4c_3x^3+⋯.\)
Utilizando la singularidad de las representaciones de series de potencia, sabemos que estas series solo pueden ser iguales si sus coeficientes son iguales. Por lo tanto,
\( c_0=c_1,\)
\( c_1=2c_2,\)
\( c_2=3c_3,\)
\( c_3=4c_4,\)
⋮
Uso de la condición inicial\( y(0)=3\) combinada con la representación de la serie de potencia
\( y(x)=c_0+c_1x+c_2x^2+c_3x^3+⋯\),
nos encontramos con eso\( c_0=3\). Ya estamos listos para resolver el resto de los coeficientes. Usando el hecho de que\( c_0=3\), tenemos
\ [\ begin {align*} c_1&=c_0=3=\ dfrac {3} {1!} ,\\ [5pt]
c_2&=\ dfrac {c_1} {2} =\ dfrac {3} {2} =\ dfrac {3} {2!} ,\\ [5pt]
c_3&=\ dfrac {c_2} {3} =\ dfrac {3} {32} =\ dfrac {3} {3!} ,\\ [5pt]
c_4&=\ dfrac {c_3} {4} =\ dfrac {3} {432} =\ dfrac {3} {4!}. \ end {alinear*}\]
Por lo tanto,
\[y=3\left[1+\dfrac{1}{1!}x+\dfrac{1}{2!}x^2+\dfrac{1}{3!}x^3\dfrac{1}{4!}x^4+⋯\right]=3\sum_{n=0}^∞\dfrac{x^n}{n!}.\nonumber \]
Podrías reconocer
\[\sum_{n=0}^∞\dfrac{x^n}{n!}\nonumber \]
como la serie Taylor para\( e^x\). Por lo tanto, la solución es\( y=3e^x\).
Utilice la serie de potencia para resolver\( y′=2y,\quad y(0)=5.\)
- Pista
-
Las ecuaciones para los primeros varios coeficientes\( c_n\) satisfarán\( c_0=2c_1,\,c_1=2⋅2c_2,\,c_2=2⋅3c_3,\,….\) En general, para todos\( n≥0,\;c_n=2(n+1)C_{n+1}\).
- Responder
-
\( y=5e^{2x}\)
Consideramos ahora un ejemplo que involucra una ecuación diferencial que no podemos resolver usando métodos previamente discutidos. Esta ecuación diferencial
\[y′−xy=0\nonumber \]
se conoce como la ecuación de Airy. Tiene muchas aplicaciones en física matemática, como modelar la difracción de luz. Aquí te mostramos cómo resolverlo usando series de potencia.
Utilice series de potencia para resolver\(y''−xy=0\) con las condiciones iniciales\( y(0)=a\) y\( y'(0)=b.\)
Solución
Buscamos una solución de la forma
\[y=\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+c_3x^3+c_4x^4+⋯\nonumber \]
Diferenciando esta función término por término, obtenemos
\ [\ begin {align*} y′&=c_1+2c_2x+3c_3x^2+4c_4x^3+,\\ [4pt]
y"&=21c_2+32c_3x+43c_4x^2+. \ end {alinear*}\]
Si\(y\) satisface la ecuación\( y''=xy\), entonces
\( 2⋅1c_2+3⋅2c_3x+4⋅3c_4x^2+⋯=x(c_0+c_1x+c_2x^2+c_3x^3+⋯).\)
Usando [link] sobre la singularidad de las representaciones de series de poder, sabemos que los coeficientes del mismo grado deben ser iguales. Por lo tanto,
\( 2⋅1c_2=0,\)
\( 3⋅2c_3=c_0,\)
\( 4⋅3c_4=c_1,\)
\( 5⋅4c_5=c_2,\)
⋮
De manera más general\( n≥3\), para, tenemos\( n⋅(n−1)c_n=c_{n−3}\). De hecho, todos los coeficientes se pueden escribir en términos de\( c_0\) y\( c_1\). Para ver esto, primero tenga en cuenta que\( c_2=0\). Entonces
\( c_3=\dfrac{c_0}{3⋅2}\),
\( c_4=\dfrac{c_1}{4⋅3}\).
Para\( c_5,\,c_6,\,c_7\), vemos que
\ [\ begin {align*} c_5&=\ dfrac {c_2} {54} =0,\\ [5pt]
c_6&=\ dfrac {c_3} {65} =\ dfrac {c_0} {6532},\\ [5pt]
c_7&=\ dfrac {c_4} {76} =\ dfrac {c_1} {7643}. \ end {alinear*}\]
Por lo tanto, la solución en serie de la ecuación diferencial viene dada por
\( y=c_0+c_1x+0⋅x^2+\dfrac{c_0}{3⋅2}x^3+\dfrac{c_1}{4⋅3}x^4+0⋅x^5+\dfrac{c_0}{6⋅5⋅3⋅2}x^6+\dfrac{c_1}{7⋅6⋅4⋅3}x^7+⋯.\)
La condición inicial\( y(0)=a\) implica\( c_0=a\). Diferenciando esta serie término por término y utilizando el hecho de que\( y′(0)=b\), concluimos que\( c_1=b\).
Por lo tanto, la solución de este problema de valor inicial es
\( y=a\left(1+\dfrac{x^3}{3⋅2}+\dfrac{x}{6⋅5⋅3⋅2}+⋯\right)+b\left(x+\dfrac{x^4}{4⋅3}+\dfrac{x^7}{7⋅6⋅4⋅3}+⋯\right).\)
Utilice series de potencia para resolver\( y''+x^2y=0\) con la condición inicial\( y(0)=a\) y\( y′(0)=b\).
- Pista
-
Los coeficientes satisfacen\( c_0=a,\,c_1=b,\,c_2=0,\,c_3=0,\) y para\( n≥4,\; n(n−1)c_n=−c_{n−4}\).
- Contestar
-
\(y=a\left(1−\dfrac{x^4}{3⋅4}+\dfrac{x^8}{3⋅4⋅7⋅8}−⋯\right)+b\left(x−\dfrac{x^5}{4⋅5}+\dfrac{x^9}{4⋅5⋅8⋅9}−⋯\right)\)
Evaluación de Integrales No Elementales
Resolver ecuaciones diferenciales es una aplicación común de las series de potencia. Pasamos ahora a una segunda aplicación. Mostramos cómo las series de potencia pueden ser utilizadas para evaluar integrales que involucran funciones cuyas antiderivadas no se pueden expresar usando funciones elementales.
Una integral que surge a menudo en las aplicaciones en la teoría de la probabilidad es\(\displaystyle \int e^{−x^2}\,dx.\) Desafortunadamente, la antiderivada del\( e^{−x^2}\) integrando no es una función elemental. Por función elemental, nos referimos a una función que se puede escribir usando un número finito de combinaciones algebraicas o composiciones de funciones exponenciales, logarítmicas, trigonométricas o de potencia. Observamos que el término “función elemental” no es sinónimo de función no complicada. Por ejemplo, la función\( f(x)=\sqrt{x^2−3x}+e^{x^3}−\sin(5x+4)\) es una función elemental, aunque no una función de aspecto particularmente simple. Cualquier integral de la forma\(\displaystyle \int f(x)\,dx\) donde la antiderivada de\( f\) no puede escribirse como una función elemental se considera una integral no elemental.
las integrales no elementales no pueden evaluarse utilizando las técnicas básicas de integración discutidas anteriormente. Una forma de evaluar tales integrales es expresando el integrando como una serie de potencias e integrando término por término. Demostramos esta técnica considerando\(\displaystyle \int e^{−x^2}\,dx.\)
- Expresar\(\displaystyle \int e^{−x^2}dx\) como una serie infinita.
- \(\displaystyle \int ^1_0e^{−x^2}dx\)Evaluar dentro de un error de\( 0.01\).
Solución
a. La serie Maclaurin para\( e^{−x^2}\) está dada por
\ [\ begin {alinear*} e^ {−x^2} &=\ suma_ {n=0} ^∞\ dfrac {(−x^2) ^n} {n!} \\ [5pt]
&=1−x^2+\ dfrac {x^4} {2!} −\ dfrac {x^6} {3!} ++ (−1) ^n\ dfrac {x^ {2n}} {n!} +\\ [5pt]
&=\ suma_ {n=0} ^∞ (−1) ^n\ dfrac {x^ {2n}} {n!}. \ end {alinear*}\]
Por lo tanto,
\ [\ begin {align*}\ int e^ {−x^2}\, dx&=\ int\ left (1−x^2+\ dfrac {x^4} {2!} −\ dfrac {x^6} {3!} ++ (−1) ^n\ dfrac {x^ {2n}} {n!} +\ derecha)\, dx\\ [5pt]
&=C+x−\ dfrac {x^3} {3} +\ dfrac {x^5} {5.2!} −\ dfrac {x^7} {7.3!} ++ (−1) ^n\ dfrac {x^ {2n+1}} {(2n+1) n!} +. \ end {alinear*}\]
b. Usando el resultado de la parte a. tenemos
\[ \int ^1_0e^{−x^2}\,dx=1−\dfrac{1}{3}+\dfrac{1}{10}−\dfrac{1}{42}+\dfrac{1}{216}−⋯.\nonumber \]
La suma de los primeros cuatro términos es aproximadamente\( 0.74\). Por la prueba de series alternas, esta estimación es precisa dentro de un error de menos de\( \dfrac{1}{216}≈0.0046296<0.01.\)
Expresar\(\displaystyle \int \cos\sqrt{x}\,dx\) como una serie infinita. \(\displaystyle \int ^1_0\cos\sqrt{x}\,dx\)Evaluar dentro de un error de\( 0.01\).
- Pista
-
Utilice la serie que se encuentra en Ejemplo\(\PageIndex{6}\).
- Contestar
-
\(\displaystyle C+\sum_{n=1}^∞(−1)^{n+1}\dfrac{x^n}{n(2n−2)!}\)La integral definida es aproximadamente\( 0.514\) a dentro de un error de\( 0.01\).
Como se mencionó anteriormente, la integral\(\displaystyle \int e^{−x^2}\,dx\) surge a menudo en la teoría de la probabilidad. Específicamente, se utiliza cuando se estudian conjuntos de datos que normalmente se distribuyen, es decir, los valores de los datos se encuentran bajo una curva en forma de campana. Por ejemplo, si un conjunto de valores de datos se distribuye normalmente con media\( μ\) y desviación estándar\( σ\), entonces la probabilidad de que un valor elegido aleatoriamente se encuentre entre\( x=a\) y\( x=b\) esté dado por
\[\dfrac{1}{σ\sqrt{2π}}\int ^b_ae^{−(x−μ)^2/(2σ^2)}\,dx.\label{probeq} \]
(Ver Figura\(\PageIndex{2}\).)
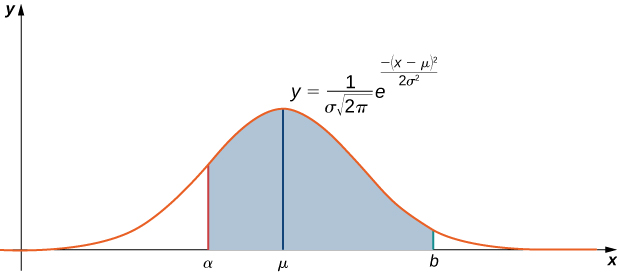
Para simplificar esta integral, solemos dejar\( z=\dfrac{x−μ}{σ}\). Esta cantidad\(z\) se conoce como la\(z\) puntuación de un valor de datos. Con esta simplificación, la Ecuación integral\ ref {probeq} se convierte en
\[\dfrac{1}{\sqrt{2π}}\int ^{(b−μ)/σ}_{(a−μ)/σ}e^{−z^2/2}\,dz. \nonumber \]
En Ejemplo\(\PageIndex{7}\), mostramos cómo podemos utilizar esta integral en el cálculo de probabilidades.
Supongamos que un conjunto de puntajes de exámenes estandarizados se distribuyen normalmente con media\( μ=100\) y desviación estándar\( σ=50\). Utilice la ecuación\ ref {probeq} y los primeros seis términos de la serie Maclaurin para\( e^{−x^2/2}\) aproximar la probabilidad de que una puntuación de prueba seleccionada aleatoriamente esté entre\( x=100\) y\( x=200\). Utilice la prueba de series alternas para determinar qué tan precisa es su aproximación.
Solución
Desde\( μ=100,σ=50,\) y estamos tratando de determinar el área bajo la curva de\( a=100\) a\( b=200\), Ecuación integral\ ref {probeq} se convierte
\[ \dfrac{1}{\sqrt{2π}}\int ^2_0e^{−z^2/2}\,dz.\nonumber \]
La serie Maclaurin para\( e^{−x^2/2}\) está dada por
\ [\ begin {align*} e^ {−x^2/2} &=\ sum_ {n=0} ^∞\ dfrac {\ left (−\ dfrac {x^2} {2}\ derecha) ^n} {n!} \\ [5pt]
&=1−\ dfrac {x^2} {2^11!} +\ dfrac {x^4} {2^22!} −\ dfrac {x^6} {2^33!} ++ (−1) ^n\ dfrac {x^ {2n}} {2^nn}! +\\ [5pt]
&=\ suma_ {n=0} ^∞ (−1) ^n\ dfrac {x^ {2n}} {2^nn!}. \ end {alinear*}\]
Por lo tanto,
\ [\ begin {align*}\ dfrac {1} {\ sqrt {2π}}\ int e^ {−z^2/2}\, dz&=\ dfrac {1} {\ sqrt {2π}}\ int\ left (1−\ dfrac {z^2} {2^11!} +\ dfrac {z^4} {2^22!} −\ dfrac {z^6} {2^33!} ++ (−1) ^n\ dfrac {z^ {2n}} {2^nn!} +\ derecha) dz\\ [5pt]
&=\ dfrac {1} {\ sqrt {2π}}\ izquierda (C+z−\ dfrac {z^3} {32^11!} +\ dfrac {z^5} {52^22!} −\ dfrac {z^7} {72^33!} ++ (−1) ^n\ dfrac {z^ {2n+1}} {(2n+1) 2^nn!} +\ derecha)\ final {alinear*}\]
\[\dfrac{1}{\sqrt{2π}}\int ^2_0e^{−z^2/2}\,dz=\dfrac{1}{\sqrt{2π}}\left(2−\dfrac{8}{6}+\dfrac{32}{40}−\dfrac{128}{336}+\dfrac{512}{3456}−\dfrac{2^{11}}{11⋅2^5⋅5!}+⋯\right)\nonumber \]
Utilizando los primeros cinco términos, estimamos que la probabilidad es de aproximadamente 0.4922. Por la prueba de series alternas, vemos que esta estimación es precisa dentro de
\[ \dfrac{1}{\sqrt{2π}}\dfrac{2^{13}}{13⋅2^6⋅6!}≈0.00546.\nonumber \]
Análisis
Si está familiarizado con la teoría de probabilidad, puede saber que la probabilidad de que un valor de datos esté dentro de dos desviaciones estándar de la media es aproximadamente\( 95\%.\) Aquí calculamos la probabilidad de que un valor de datos esté entre la media y dos desviaciones estándar por encima de la media, por lo que la estimación debe ser alrededor\( 47.5\%\). La estimación, combinada con el límite en la precisión, se encuentra dentro de este rango.
Utilice los primeros cinco términos de la serie Maclaurin\( e^{−x^2/2}\) para estimar la probabilidad de que una puntuación de prueba seleccionada al azar esté entre\( 100\) y\( 150\). Utilice la prueba de series alternas para determinar la precisión de esta estimación.
- Pista
-
Evaluar\(\displaystyle \int ^1_0e^{−z^2/2}\,dz\) utilizando los primeros cinco términos de la serie Maclaurin para\( e^{−z^2/2}\).
- Contestar
-
La estimación es aproximadamente\( 0.3414.\) Esta estimación es precisa dentro de\( 0.0000094.\)
Otra aplicación en la que surge una integral no elemental involucra el periodo de un péndulo. La integral es
\[\int ^{π/2}_0\dfrac{dθ}{\sqrt{1−k^2\sin^2θ}}\nonumber \].
Una integral de esta forma se conoce como una integral elíptica de primer tipo. Las integrales elípticas surgieron originalmente al intentar calcular la longitud del arco de una elipse. Ahora mostramos cómo usar series de potencia para aproximar esta integral.
El período de un péndulo es el tiempo que tarda un péndulo en hacer una oscilación completa de ida y vuelta. Para un péndulo con longitud\( L\) que hace un ángulo máximo\( θ_{max}\) con la vertical, su periodo\( T\) viene dado por
\[ T=4\sqrt{\dfrac{L}{g}}\int ^{π/2}_0\dfrac{dθ}{\sqrt{1−k^2\sin^2θ}}\nonumber \]
donde\( g\) esta la aceleracion debida a la gravedad y\( k=\sin\left(\dfrac{θ_{max}}{2}\right)\) (ver Figura\(\PageIndex{3}\)). (Observamos que esta fórmula para el periodo surge de un modelo no linealizado de un péndulo. En algunos casos, para la simplificación, se utiliza un modelo linealizado y\(\sin θ\) se aproxima por\( θ\).)
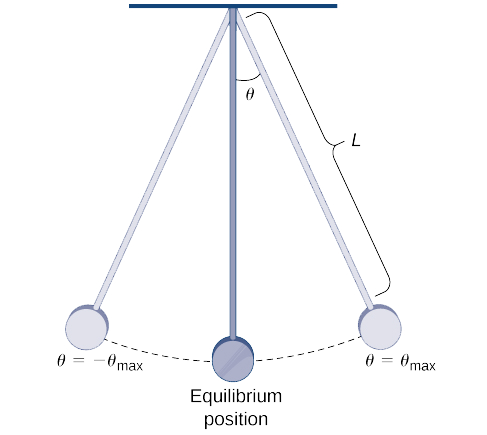
Usar la serie binomial
\[ \dfrac{1}{\sqrt{1+x}}=1+\sum_{n=1}^∞\dfrac{(−1)^n}{n!}\dfrac{1⋅3⋅5⋯(2n−1)}{2^n}x^n\nonumber \]
para estimar el periodo de este péndulo. Específicamente, aproximar el periodo del péndulo si
- usa solo el primer término en la serie binomial, y
- usa los dos primeros términos de la serie binomial.
Solución
Usamos la serie binomial, reemplazando x con\( −k^2\sin^2θ.\) Entonces podemos escribir el periodo como
\[ T=4\sqrt{\dfrac{L}{g}}\int ^{π/2}_0\left(1+\dfrac{1}{2}k^2\sin^2θ+\dfrac{1⋅3}{2!2^2}k^4\sin^4θ+⋯\right)\,dθ.\nonumber \]
a. Utilizando solo el primer término en el integrando, la estimación de primer orden es
\[ T≈4\sqrt{\dfrac{L}{g}}\int ^{π/2}_0\,dθ=2π\sqrt{\dfrac{L}{g}}.\nonumber \]
Si\( θ_{max}\) es pequeño, entonces\( k=\sin\left(\dfrac{θ_{max}}{2}\right)\) es pequeño. Afirmamos que cuando\( k\) es pequeño, esta es una buena estimación. Para justificar esta alegación, considere
\[ \int ^{π/2}_0\left(1+\frac{1}{2}k^2\sin^2θ+\dfrac{1⋅3}{2!2^2}k^4\sin^4θ+⋯\right)\,dθ.\nonumber \]
Ya que\( |\sin x|≤1\), esta integral está delimitada por
\[ \int ^{π/2}_0\left(\dfrac{1}{2}k^2+\dfrac{1.3}{2!2^2}k^4+⋯\right)\,dθ\;<\;\dfrac{π}{2}\left(\dfrac{1}{2}k^2+\dfrac{1⋅3}{2!2^2}k^4+⋯\right).\nonumber \]
Además, se puede demostrar que cada coeficiente del lado derecho es menor que\( 1\) y, por lo tanto, que esta expresión está delimitada por
\( \dfrac{πk^2}{2}(1+k^2+k^4+⋯)=\dfrac{πk^2}{2}⋅\dfrac{1}{1−k^2}\),
que es pequeño para\( k\) pequeño.
b. Para valores mayores de\( θ_{max}\), podemos aproximarnos\( T\) usando más términos en el integrando. Al utilizar los dos primeros términos en la integral, llegamos a la estimación
\[ T≈4\sqrt{\frac{L}{g}}\int ^{π/2}_0\left(1+\dfrac{1}{2}k^2\sin^2θ\right)\,dθ=2π\sqrt{\dfrac{L}{g}}\left(1+\dfrac{k^2}{4}\right).\nonumber \]
Las aplicaciones de la serie Taylor en esta sección pretenden resaltar su importancia. En general, las series Taylor son útiles porque nos permiten representar funciones conocidas utilizando polinomios, proporcionándonos así una herramienta para aproximar valores de función y estimar integrales complicadas. Además, nos permiten definir nuevas funciones como series de potencia, proporcionándonos así una poderosa herramienta para resolver ecuaciones diferenciales.
Conceptos clave
- La serie binomial es la serie Maclaurin para\( f(x)=(1+x)^r\). Converge para\( |x|<1\).
- La serie Taylor para funciones a menudo se puede derivar por operaciones algebraicas con una serie Taylor conocida o diferenciando o integrando una serie Taylor conocida.
- Las series de potencia se pueden utilizar para resolver ecuaciones diferenciales.
- La serie Taylor se puede utilizar para ayudar a aproximar integrales que no pueden ser evaluadas por otros medios.
Glosario
- serie binomial
- la serie Maclaurin para\( f(x)=(1+x)^r\); está dada por\(\displaystyle (1+x)^r=\sum_{n=0}^∞\binom{r}{n}x^n=1+rx+\dfrac{r(r−1)}{2!}x^2+⋯+\dfrac{r(r−1)⋯(r−n+1)}{n!}x^n+⋯\) para\( |x|<1\)
- integral no elemental
- una integral para la cual la antiderivada del integrando no puede expresarse como una función elemental