10.3: Serie Taylor y Maclaurin

Objetivos de aprendizaje

• Describir el procedimiento para encontrar un polinomio Taylor de un orden determinado para una función.
• Explicar el significado y significado del teorema de Taylor con resto.
• Estimar el resto para una aproximación de la serie Taylor de una función dada.

En las dos secciones anteriores discutimos cómo encontrar representaciones de series de potencia para ciertos tipos de funciones, específicamente, funciones relacionadas con series geométricas. Aquí discutimos representaciones de series de potencia para otros tipos de funciones. En particular, abordamos las siguientes preguntas: ¿Qué funciones se pueden representar por series de poder y cómo encontramos tales representaciones? Si podemos encontrar una representación de series de potencia para una función en particular$f$ y la serie converge en algún intervalo, ¿cómo demostramos que la serie realmente converge a$f$?

Descripción general de la serie Taylor/Maclaurin

Considere una función$f$ que tenga una representación de serie de potencia en$x=a$. Entonces la serie tiene la forma

$$\sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(x−a)+c_2(x−a)^2+ \dots. \label{eq1}$$

¿Cuáles deberían ser los coeficientes? Por ahora, ignoramos los temas de convergencia, pero en cambio nos centramos en lo que debería ser la serie, si existe una. Volvemos a discutir la convergencia más adelante en esta sección. Si la serie Ecuación\ ref {eq1} es una representación para$f$ at$x=a$, ciertamente queremos que la serie sea igual a$f(a)$ at$x=a$. Evaluando la serie en$x=a$, vemos que

$$\sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(a−a)+c_2(a−a)^2+\dots=c_0.\label{eq2}$$

Así, la serie es igual$f(a)$ si el coeficiente$c_0=f(a)$. Además, nos gustaría que la primera derivada de la serie power iguale$f′(a)$ en$x=a$. Ecuación diferenciadora\ ref {eq2} término por término, vemos que

$$\dfrac{d}{dx}\left( \sum_{n=0}^∞c_n(x−a)^n \right)=c_1+2c_2(x−a)+3c_3(x−a)^2+\dots.\label{eq3}$$

Por lo tanto, en$x=a,$ la derivada es

$$\dfrac{d}{dx}\left( \sum_{n=0}^∞c_n(x−a)^n \right)=c_1+2c_2(a−a)+3c_3(a−a)^2+\dots=c_1.\label{eq4}$$

Por lo tanto, la derivada de la serie es igual$f′(a)$ si el coeficiente$c_1=f′(a).$ Continuando de esta manera, buscamos coeficientes$c_n$ tales que todas las derivadas de la serie de potencias Ecuación\ ref {eq4} coincidan con todas las derivadas correspondientes de$f$ at$x=a$. La segunda y tercera derivadas de la Ecuación\ ref {eq3} vienen dadas por

$$\dfrac{d^2}{dx^2} \left(\sum_{n=0}^∞c_n(x−a)^n \right)=2c_2+3⋅2c_3(x−a)+4⋅3c_4(x−a)^2+\dots\label{eq5}$$

y

$$\dfrac{d^3}{dx^3} \left( \sum_{n=0}^∞c_n(x−a)^n \right)=3⋅2c_3+4⋅3⋅2c_4(x−a)+5⋅4⋅3c_5(x−a)^2+⋯.\label{eq6}$$

Por lo tanto$x=a$, en, el segundo y tercer derivados

$$\dfrac{d^2}{dx^2} \left(\sum_{n=0}^∞c_n(x−a)^n\right)=2c_2+3⋅2c_3(a−a)+4⋅3c_4(a−a)^2+\dots=2c_2\label{eq7}$$

y

$$\dfrac{d^3}{dx^3} \left(\sum_{n=0}^∞c_n(x−a)^n\right)=3⋅2c_3+4⋅3⋅2c_4(a−a)+5⋅4⋅3c_5(a−a)^2+\dots =3⋅2c_3\label{eq8}$$

igual$f''(a)$ y$f'''(a)$, respectivamente, si$c_2=\dfrac{f''(a)}{2}$ y$c_3=\dfrac{f'''(a)}{3⋅2}$. De manera más general, vemos que si$f$ tiene una representación de serie de potencia en$x=a$, entonces los coeficientes deben ser dados por$c_n=\dfrac{f^{(n)}(a)}{n!}$. Es decir, la serie debería ser

$$\sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+\dfrac{f'''(a)}{3!}(x−a)^3+⋯ \nonumber$$

Esta serie de poder para$f$ es conocida como la serie Taylor para$f$ en$a.$ If$x=0$, entonces esta serie es conocida como la serie Maclaurin para$f$.

Definición$\PageIndex{1}$: Maclaurin and Taylor series

Si$f$ tiene derivados de todos los pedidos en$x=a$, entonces la serie Taylor para la función$f$ at$a$ es

$$\sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n+⋯ \nonumber$$

La serie de Taylor para$f$ a 0 es conocida como la serie Maclaurin para$f$.

Más adelante en esta sección, mostraremos ejemplos de encontrar series de Taylor y discutiremos las condiciones bajo las cuales la serie Taylor para una función convergerá a esa función. Aquí, señalamos un resultado importante. Recordemos que las representaciones de series de poder son únicas. Por lo tanto, si una función$f$ tiene una serie power at$a$, entonces debe ser la serie Taylor para$f$ at$a$.

Singularidad de la serie Taylor

Si una función$f$ tiene una serie de potencia en una que converge$f$ en algún intervalo abierto que contiene$a$, entonces esa serie de potencia es la serie Taylor para$f$ at$a$.

La prueba se desprende directamente de lo discutido anteriormente.

Para determinar si una serie de Taylor converge, necesitamos mirar su secuencia de sumas parciales. Estas sumas parciales son polinomios finitos, conocidos como polinomios de Taylor.

Polinomios de Taylor

La suma$n^{\text{th}}$ parcial de la serie Taylor para una función$f$ at$a$ se conoce como polinomio de Taylor de$n^{\text{th}}$ grado. Por ejemplo, las sumas parciales 0 ^th, 1 ^st, 2 ^nd y 3 ^rd de la serie Taylor están dadas por

$$\begin{align*} p_0(x) &=f(a) \\[4pt] p_1(x) &=f(a)+f′(a)(x−a) \\[4pt]p_2(x) &=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2\ \\[4pt]p_3(x) &=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+\dfrac{f'''(a)}{3!}(x−a)^3 \end{align*}$$

respectivamente. Estas sumas parciales se conocen como los polinomios Taylor de 0 ^th, 1 ^st, 2 ^nd y 3 ^rd grado de$f$ at$a$, respectivamente. Si$x=a$, entonces estos polinomios se conocen como polinomios de Maclaurin para$f$. Ahora proporcionamos una definición formal de polinomios de Taylor y Maclaurin para una función$f$.

Definición$\PageIndex{2}$: Maclaurin polynomial

Si$f$ tiene$n$ derivados en$x=a$, entonces el polinomio de Taylor de$n^{\text{th}}$ -grado de$f$ at$a$ es

$$p_n(x)=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+\dfrac{f'''(a)}{3!}(x−a)^3+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n. \nonumber$$

El polinomio de$n^{\text{th}}$ -grado Taylor para$f$ at$0$ se conoce como el polinomio de$n^{\text{th}}$ -grado Maclaurin para$f$.

Ahora mostramos cómo usar esta definición para encontrar varios polinomios de Taylor para$f(x)=\ln x$ at$x=1$.

Ejemplo$\PageIndex{1}$: Finding Taylor Polynomials

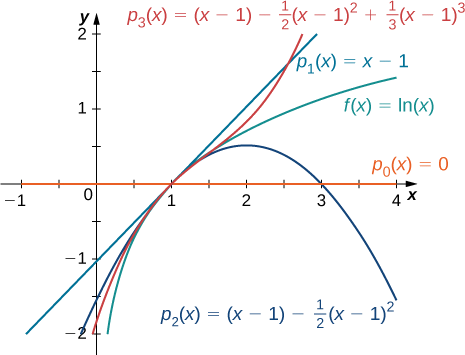
Encuentra los polinomios de Taylor$p_0,p_1,p_2$ y$p_3$ para$f(x)=\ln x$ en$x=1$. Utilice una utilidad gráfica para comparar la gráfica de$f$ con las gráficas de$p_0,p_1,p_2$ y$p_3$.

Solución

Para encontrar estos polinomios de Taylor, necesitamos evaluar$f$ y sus tres primeras derivadas en$x=1$.

\ [\ begin {alinear*} f (x) &=\ ln x & f (1) &=0\\ [5pt]
f′ (x) &=\ dfrac {1} {x} & f′ (1) &=1\\ [5pt]
f "(x) &=−\ dfrac {1} {x^2} & f" (1) &=−1\ [5pt]
f"' (x) &=\ dfrac {2} {x^3} & f"' (1) &=2\ end {align*}\]

Por lo tanto,

$$\begin{align*} p_0(x) &= f(1)=0,\\[4pt]p_1(x) &=f(1)+f′(1)(x−1) =x−1,\\[4pt]p_2(x) &=f(1)+f′(1)(x−1)+\dfrac{f''(1)}{2}(x−1)^2 = (x−1)−\dfrac{1}{2}(x−1)^2 \\[4pt]p_3(x) &=f(1)+f′(1)(x−1)+\dfrac{f''(1)}{2}(x−1)^2+\dfrac{f'''(1)}{3!}(x−1)^3=(x−1)−\dfrac{1}{2}(x−1)^2+\dfrac{1}{3}(x−1)^3 \end{align*}$$

Las gráficas$y=f(x)$ y los tres primeros polinomios de Taylor se muestran en la Figura$\PageIndex{1}$.

Figura$\PageIndex{1}$: La función$y=\ln x$ y los polinomios Taylor$p_0,p_1,p_2$ y$p_3$ at$x=1$ se trazan en esta gráfica.

Ejercicio$\PageIndex{1}$

Encuentra los polinomios de Taylor$p_0,p_1,p_2$ y$p_3$ para$f(x)=\dfrac{1}{x^2}$ en$x=1$.

Pista

Encuentre las tres primeras derivadas de$f$ y evalúelas en$x=1.$

Contestar

\ [\ begin {alinear*} p_0 (x) &=1\\ [5pt]
p_1 (x) &=1−2 (x−1)\\ [5pt]
p_2 (x) &=1−2 (x−1) +3 (x−1) ^2\\ [5pt]
p_3 (x) &=1−2 (x−1) +3 (x−1) ^2−4 (x−1) ^3\ end {alinear*}\]

Ahora mostramos cómo encontrar polinomios de Maclaurin para$e^x, \sin x,$ y$\cos x$. Como se indicó anteriormente, los polinomios de Maclaurin son polinomios de Taylor centrados en cero.

Ejemplo$\PageIndex{2}$: Finding Maclaurin Polynomials

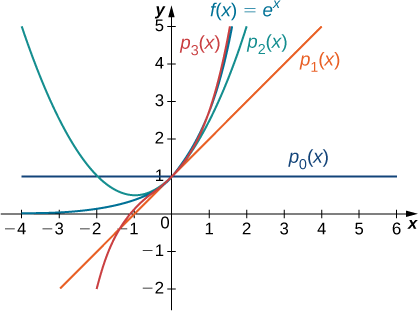
Para cada una de las siguientes funciones, encuentre fórmulas para los polinomios Maclaurin$p_0,p_1,p_2$ y$p_3$. Encuentra una fórmula para el polinomio de Maclaurin de$n^{\text{th}}$ grado y escríbala usando notación sigma. Utilice una utilidad gráfica para comparar las gráficas de$p_0,p_1,p_2$ y$p_3$ con$f$.

1. $f(x)=e^x$
2. $f(x)=\sin x$
3. $f(x)=\cos x$

Solución

Ya que$f(x)=e^x$, sabemos que$f(x)=f′(x)=f''(x)=⋯=f^{(n)}(x)=e^x$ para todos los enteros positivos$n$. Por lo tanto,

$$f(0)=f′(0)=f''(0)=⋯=f^{(n)}(0)=1 \nonumber$$

para todos los enteros positivos$n$. Por lo tanto, tenemos

\ (\ begin {align*} p_0 (x) &=f (0) =1,\\ [5pt]
p_1 (x) &=f (0) +f′ (0) x=1+x,\\ [5pt]
p_2 (x) &=f (0) +f′ (0) x+\ dfrac {f "(0)} {2!} x^2=1+x+\ dfrac {1} {2} x^2,\\ [5pt]
p_3 (x) &=f (0) +f′ (0) x+\ dfrac {f "(0)} {2} x^2+\ dfrac {f"' (0)} {3!} x^3=1+x+\ dfrac {1} {2} x^2+\ dfrac {1} {3!} x^3,\ end {alinear*}\)

\ (\ displaystyle\ begin {alinear*} p_n (x) &=f (0) +f′ (0) x+\ dfrac {f "(0)} {2} x^2+\ dfrac {f"' (0)} {3!} x^3++\ dfrac {f^ {(n)} (0)} {n!} x^n\\ [5pt]
&=1+x+\ dfrac {x^2} {2!} +\ dfrac {x^3} {3!} ++\ dfrac {x^n} {n!} \\ [5pt]
&=\ suma_ {k=0} ^n\ dfrac {x^k} {k!} \ end {align*}\).

La función y los tres primeros polinomios de Maclaurin se muestran en la Figura$\PageIndex{2}$.

Figura$\PageIndex{2}$: La gráfica muestra la función$y=e^x$ y los polinomios de Maclaurin$p_0,\,p_1,\,p_2$ y$p_3$.

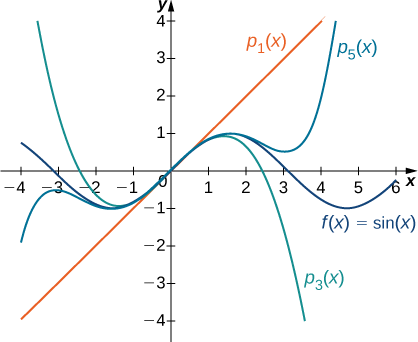
b. Para$f(x)=\sin x$, los valores de la función y sus primeras cuatro derivadas at$x=0$ se dan de la siguiente manera:

\ [\ begin {align*} f (x) &=\ sin x & f (0) &=0\\ [5pt]
f′ (x) &=\ cos x & f′ (0) &=1\\ [5pt]
f "(x) &=−\ sin x & f" (0) &=0\\ [5pt]
f"' (x) &=− cos x & f"' (0) &=−1\\ [5pt]
f^ {(4)} (x) &=\ sin x & f^ {(4)} (0) &=0. \ end {alinear*}\]

Dado que la cuarta derivada es$\sin x,$ el patrón se repite. Es decir,$f^{(2m)}(0)=0$ y$f^{(2m+1)}(0)=(−1)^m$ por$m≥0.$ lo tanto, tenemos

\ (\ begin {align*} p_0 (x) &=0,\\ [5pt]
p_1 (x) &=0+x=x,\\ [5pt]
p_2 (x) &=0+x+0=x,\\ [5pt]
p_3 (x) &=0+x+0−\ dfrac {1} {3!} x^3=x−\ dfrac {x^3} {3!} ,\\ [5pt]
p_4 (x) &=0+x+0−\ dfrac {1} {3!} x^3+0=x−\ dfrac {x^3} {3!} ,\\ [5pt]
p_5 (x) &=0+x+0−\ dfrac {1} {3!} x^3+0+\ dfrac {1} {5!} x^5=x−\ dfrac {x^3} {3!} +\ dfrac {x^5} {5!} ,\ end {alinear*}\)

y para$m≥0$,

\ [\ begin {alinear*} p_ {2m+1} (x) =p_ {2m+2} (x) &=x−\ dfrac {x^3} {3!} +\ dfrac {x^5} {5!} −+ (−1) ^m\ dfrac {x^ {2m+1}} {(2m+1)!} \\ [5pt]
&=\ sum_ {k=0} ^m (−1) ^k\ dfrac {x^ {2k+1}} {(2k+1)!}. \ end {alinear*}\]

Las gráficas de la función y sus polinomios Maclaurin se muestran en la Figura$\PageIndex{3}$.

Figura$\PageIndex{3}$: La gráfica muestra la función$y=\sin x$ y los polinomios de Maclaurin$p_1,\, p_3$ y$p_5$.

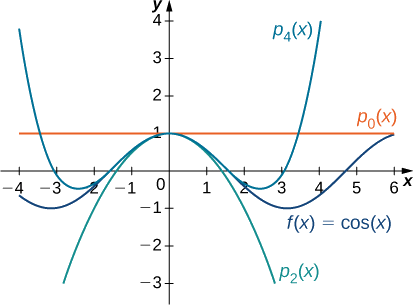
c. Para$f(x)=\cos x$, los valores de la función y sus primeras cuatro derivadas at$x=0$ se dan de la siguiente manera:

\ [\ begin {alinear*} f (x) &=\ cos x & f (0) &=1\\ [5pt]
f′ (x) &=−\ sin x & f′ (0) &=0\\ [5pt]
f "(x) &=−\ cos x & f" (0) &=−1\\ [5pt]
f"' (x) &=\ sin x & f"' (0) &=0\\ [5pt]
f^ {(4)} (x) &=\ cos x & f^ {(4)} (0) &=1. \ end {alinear*}\]

Dado que la cuarta derivada es$\sin x$, el patrón se repite. En otras palabras,$f^{(2m)}(0)=(−1)^m$ y$f^{(2m+1)}=0$ para$m≥0$. Por lo tanto,

\ (\ begin {align*} p_0 (x) &=1,\\ [5pt]
p_1 (x) &=1+0=1,\\ [5pt]
p_2 (x) &=1+0−\ dfrac {1} {2!} x^2=1−\ dfrac {x^2} {2!} ,\\ [5pt]
p_3 (x) &=1+0−\ dfrac {1} {2!} x^2+0=1−\ dfrac {x^2} {2!} ,\\ [5pt]
p_4 (x) &=1+0−\ dfrac {1} {2!} x^2+0+\ dfrac {1} {4!} x^4=1−\ dfrac {x^2} {2!} +\ dfrac {x^4} {4!} ,\\ [5pt]
p_5 (x) &=1+0−\ dfrac {1} {2!} x^2+0+\ dfrac {1} {4!} x^4+0=1−\ dfrac {x^2} {2!} +\ dfrac {x^4} {4!} ,\ end {alinear*}\)

y para$n≥0$,

\ [\ begin {alinear*} p_ {2m} (x) &=p_ {2m+1} (x)\\ [5pt]
&=1−\ dfrac {x^2} {2!} +\ dfrac {x^4} {4!} −+ (−1) ^m\ dfrac {x^ {2m}} {(2m)!} \\ [5pt]
&=\ sum_ {k=0} ^m (−1) ^k\ dfrac {x^ {2k}} {(2k)!}. \ end {alinear*}\]

Las gráficas de la función y los polinomios de Maclaurin aparecen en la Figura$\PageIndex{4}$.

Figura$\PageIndex{4}$: La función$y=\cos x$ y los polinomios Maclaurin$p_0,p_2$ y$p_4$ se trazan en esta gráfica.

Ejercicio$\PageIndex{2}$

Encuentra fórmulas para los polinomios Maclaurin$p_0,\,p_1,\,p_2$ y$p_3$ para$f(x)=\dfrac{1}{1+x}$.

Encuentra una fórmula para el polinomio de Maclaurin de$n^{\text{th}}$ grado. Escribe tu respuesta usando notación sigma.

Pista

Evaluar las primeras cuatro derivadas de$f$ y buscar un patrón.

Contestar

$\displaystyle p_0(x)=1;\;p_1(x)=1−x;\;p_2(x)=1−x+x^2;\;p_3(x)=1−x+x^2−x^3;\;p_n(x)=1−x+x^2−x^3+⋯+(−1)^nx^n=\sum_{k=0}^n(−1)^kx^k$

Teorema de Taylor con el resto

Recordemos que el polinomio de Taylor$n^{\text{th}}$ -grado para una función$f$ at$a$ es la suma$n^{\text{th}}$ parcial de la serie Taylor para$f$ at$a$. Por lo tanto, para determinar si la serie Taylor converge, necesitamos determinar si la secuencia de polinomios de Taylor${p_n}$ converge. No obstante, no sólo queremos saber si la secuencia de polinomios Taylor converge, queremos saber si converge a$f$. Para responder a esta pregunta, definimos el resto$R_n(x)$ como

$$R_n(x)=f(x)−p_n(x). \nonumber$$

Para que la secuencia de polinomios de Taylor converja$f$, necesitamos que el resto converja$R_n$ a cero. Para determinar si$R_n$ converge a cero, introducimos el teorema de Taylor con el resto. Este teorema no sólo es útil para demostrar que una serie de Taylor converge a su función relacionada, sino que también nos permitirá cuantificar qué tan bien el polinomio Taylor de$n^{\text{th}}$ grado se aproxima a la función.

Aquí buscamos un encuadernado en$|R_n|.$ Considere el caso más simple:$n=0$. $p_0$Sea el 0 ^º polinomio de Taylor en$a$ para una función$f$. El resto$R_0$ satisface

$R_0(x)=f(x)−p_0(x)=f(x)−f(a).$

Si$f$ es diferenciable en un intervalo$I$ que contiene$a$ y$x$, entonces por el Teorema del Valor Medio existe un número real$c$ entre$a$ y$x$ tal que$f(x)−f(a)=f′(c)(x−a)$. Por lo tanto,

$$R_0(x)=f′(c)(x−a). \nonumber$$

Usando el Teorema del Valor Medio en un argumento similar, podemos mostrar que si$f$ es$n$ tiempos diferenciables en un intervalo$I$ que contiene$a$ y$x$, entonces el$n^{\text{th}}$ resto$R_n$ satisface

$$R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1} \nonumber$$

para algún número real$c$ entre$a$ y$x$. Es importante señalar que el valor$c$ en el numerador anterior no es el centro$a$, sino un valor desconocido$c$ entre$a$ y$x$. Esta fórmula nos permite obtener un límite sobre el resto$R_n$. Si por casualidad sabemos que$∣f^{(n+1)}(x)∣$ está delimitado por algún número real$M$ en este intervalo$I$, entonces

$$|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber$$

para todos$x$ en el intervalo$I$.

Ahora declaramos el teorema de Taylor, que proporciona la relación formal entre una función$f$ y su polinomio de Taylor de$n^{\text{th}}$ grado$p_n(x)$. Este teorema nos permite encuadernar el error al usar un polinomio de Taylor para aproximar un valor de función, y será importante para probar que una serie de Taylor para$f$ converge a$f$.

Teorema de Taylor con el resto

Dejar$f$ ser una función que pueda diferenciarse$n+1$ tiempos en un intervalo$I$ que contenga el número real$a$. Dejar$p_n$ ser el polinomio de Taylor$n^{\text{th}}$ -grado de$f$ at$a$ y dejar

$$R_n(x)=f(x)−p_n(x) \nonumber$$

ser el$n^{\text{th}}$ resto. Entonces para cada uno$x$ en el intervalo$I$, existe un número real$c$ entre$a$ y$x$ tal que

$$R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1} \nonumber$$ .

Si existe un número real$M$ tal que$∣f^{(n+1)}(x)∣≤M$ para todos$x∈I$, entonces

$$|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber$$

para todos$x$ en$I$.

Prueba

Fijar un punto$x∈I$ e introducir la función de$g$ tal manera que

$$g(t)=f(x)−f(t)−f′(t)(x−t)−\dfrac{f''(t)}{2!}(x−t)^2−⋯−\dfrac{f^{(n)}(t)}{n!}(x−t)^n−R_n(x)\dfrac{(x−t)^{n+1}}{(x−a)^{n+1}}. \nonumber$$

Afirmamos que$g$ satisface los criterios del teorema de Rolle. Dado que$g$ es una función polinómica (in$t$), es una función diferenciable. Además,$g$ es cero en$t=a$ y$t=x$ porque

$$\begin{align*} g(a) &=f(x)−f(a)−f′(a)(x−a)−\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n−R_n(x) \\[4pt] &=f(x)−p_n(x)−R_n(x) \\[4pt] &=0, \\[4pt] g(x) &=f(x)−f(x)−0−⋯−0 \\[4pt] &=0. \end{align*}$$

Por lo tanto,$g$ satisface el teorema de Rolle, y en consecuencia, existe$c$ entre$a$ y$x$ tal que ahora$g′(c)=0.$ calculamos$g′$. Usando la regla del producto, observamos que

$$\dfrac{d}{dt}\left[\dfrac{f^{(n)}(t)}{n!}(x−t)^n\right]=−\dfrac{f^{(n)}(t)}{(n−1)!}(x−t)^{n−1}+\dfrac{f^{(n+1)}(t)}{n!}(x−t)^n. \nonumber$$

En consecuencia,

\ [\ begin {align} g′ (t) &=−f′ (t) + [f′ (t) −f "(t) (x−t)] +\ left [f" (t) (x−t) −\ dfrac {f"' (t)} {2!} (x−t) ^2\ derecha] +\ nonumber\\
&\ quad+\ left [\ dfrac {f^ {(n)} (t)} {(n−1)!} (x−t) ^ {n−1} −\ dfrac {f^ {(n+1)} (t)} {n!} (x−t) ^n\ derecha] + (n+1) r_n (x)\ dfrac {(x−t) ^n} {(x−a) ^ {n+1}}\ end {align}\ nonumber\].

Observe que hay un efecto telescópico. Por lo tanto,

$$g'(t)=−\dfrac{f^{(n+1)}(t)}{n!}(x−t)^n+(n+1)R_n(x)\dfrac{(x−t)^n}{(x−a)^{n+1}} \nonumber$$ .

Por el teorema de Rolle, concluimos que existe un número$c$ entre$a$ y$x$ tal que$g′(c)=0.$ Desde

$$g′(c)=−\dfrac{f^{(n+1})(c)}{n!}(x−c)^n+(n+1)R_n(x)\dfrac{(x−c)^n}{(x−a)^{n+1}} \nonumber$$

concluimos que

$$−\dfrac{f^{(n+1)}(c)}{n!}(x−c)^n+(n+1)R_n(x)\dfrac{(x−c)^n}{(x−a)^{n+1}}=0. \nonumber$$

Añadiendo el primer término en el lado izquierdo a ambos lados de la ecuación y dividiendo ambos lados de la ecuación por$n+1,$ concluimos que

$$R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1} \nonumber$$

según se desee. De este hecho, se deduce que si existe$M$ tal que$∣f^{(n+1)}(x)∣≤M$ para todos$x$ en$I$, entonces

$$|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber$$ .

□

El teorema de Taylor no solo nos permite probar que una serie de Taylor converge a una función, sino que también nos permite estimar la precisión de los polinomios de Taylor en la aproximación de valores de función. Comenzamos observando aproximaciones lineales y cuadráticas de$f(x)=\sqrt[3]{x}$ at$x=8$ y determinamos qué tan precisas son estas aproximaciones en la estimación$\sqrt[3]{11}$.

Ejemplo$\PageIndex{3}$: Using Linear and Quadratic Approximations to Estimate Function Values

Considera la función$f(x)=\sqrt[3]{x}$.

1. Encuentra el primer y segundo polinomios de Taylor para$f$ al$x=8$. Utilice una utilidad gráfica para comparar estos polinomios con$f$ cerca$x=8.$
2. Utilice estos dos polinomios para estimar$\sqrt[3]{11}$.
3. Usa el teorema de Taylor para encuadernar el error.

Solución:

a. para$f(x)=\sqrt[3]{x}$, los valores de la función y sus dos primeras derivadas at$x=8$ son los siguientes:

\ [\ begin {alinear*} f (x) &=\ sqrt [3] {x}, & f (8) &=2\\ [5pt]
f′ (x) &=\ dfrac {1} {3x^ {2/3}}, & f′ (8) &=\ dfrac {1} {12}\\ [5pt] f "(x) &=\ dfrac {1}\\ [5pt]
f" (x) &=\ dfrac {1}\\ [5pt] ac {−2} {9x^ {5/3}}, & f "(8) &=−\ dfrac {1} {144.} \ end {alinear*}\]

Así, los polinomios de Taylor primero y segundo$x=8$ están dados por

\ (\ begin {align*} p_1 (x) &=f (8) +f′ (8) (x−8)\\ [5pt]
&=2+\ dfrac {1} {12} (x−8)\ end {alinear*}\)

\ (\ begin {alinear*} p_2 (x) &=f (8) +f′ (8) (x−8) +\ dfrac {f "(8)} {2!} (x−8) ^2\\ [5pt]
&=2+\ dfrac {1} {12} (x−8) −\ dfrac {1} {288} (x−8) ^2. \ end {alinear*}\)

La función y los polinomios de Taylor se muestran en la Figura$\PageIndex{5}$.

Figura$\PageIndex{5}$: Las gráficas de$f(x)=\sqrt[3]{x}$ y las aproximaciones lineales y cuadráticas$p_1(x)$ y$p_2(x)$

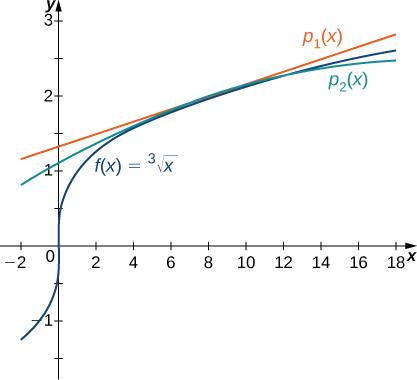
b. Usando el primer polinomio de Taylor en$x=8$, podemos estimar

$$\sqrt[3]{11}≈p_1(11)=2+\dfrac{1}{12}(11−8)=2.25. \nonumber$$

Usando el segundo polinomio de Taylor en$x=8$, obtenemos

$$\sqrt[3]{11}≈p_2(11)=2+\dfrac{1}{12}(11−8)−\dfrac{1}{288}(11−8)^2=2.21875. \nonumber$$

c. Por Nota, existe una c en el intervalo$(8,11)$ tal que el resto al aproximarse$\sqrt[3]{11}$ por el primer polinomio de Taylor satisface

$$R_1(11)=\dfrac{f''(c)}{2!}(11−8)^2. \nonumber$$

No conocemos el valor exacto de$c,$ por lo que encontramos un límite superior en$R_1(11)$ determinando el valor máximo de$f''$ en el intervalo$(8,11)$. Ya que$f''(x)=−\dfrac{2}{9x^{5/3}}$, el valor más grande para$|f''(x)|$ en ese intervalo ocurre en$x=8$. Utilizando el hecho de que$f''(8)=−\dfrac{1}{144}$, obtenemos

$|R_1(11)|≤\dfrac{1}{144⋅2!}(11−8)^2=0.03125.$

Del mismo modo, para estimar$R_2(11)$, utilizamos el hecho de que

$R_2(11)=\dfrac{f'''(c)}{3!}(11−8)^3$.

Ya que$f'''(x)=\dfrac{10}{27x^{8/3}}$, el valor máximo de$f'''$ en el intervalo$(8,11)$ es$f'''(8)≈0.0014468$. Por lo tanto, tenemos

$|R_2(11)|≤\dfrac{0.0011468}{3!}(11−8)^3≈0.0065104.$

Ejercicio$\PageIndex{3}$:

Encuentra el primer y segundo polinomios de Taylor para$f(x)=\sqrt{x}$ al$x=4$. Utilice estos polinomios para estimar$\sqrt{6}$. Usa el teorema de Taylor para encuadernar el error.

Pista

Evaluar$f(4),f′(4),$ y$f''(4).$

Contestar

$p_1(x)=2+\dfrac{1}{4}(x−4);p_2(x)=2+\dfrac{1}{4}(x−4)−\dfrac{1}{64}(x−4)^2;p_1(6)=2.5;p_2(6)=2.4375;$

$|R_1(6)|≤0.0625;|R_2(6)|≤0.015625$

Ejemplo$\PageIndex{4}$: Approximating $\sin x$ Using Maclaurin Polynomials

De Ejemplo$\PageIndex{2b}$, los polinomios de Maclaurin para$\sin x$ están dados por

$$p_{2m+1}(x)=p_{2m+2}(x)=x−\dfrac{x^3}{3!}+\dfrac{x^5}{5!}−\dfrac{x^7}{7!}+⋯+(−1)^m\dfrac{x^{2m+1}}{(2m+1)!} \nonumber$$

para$m=0,1,2,….$

1. Utilice el quinto polinomio Maclaurin para$\sin x$ aproximar$\sin\left(\dfrac{π}{18}\right)$ y encuadernar el error.
2. ¿Para qué valores del$x$ quinto polinomio Maclaurin se$\sin x$ aproxima al interior$0.0001$?

Solución

a.

El quinto polinomio de Maclaurin es

$$p_5(x)=x−\dfrac{x^3}{3!}+\dfrac{x^5}{5!} \nonumber$$ .

Usando este polinomio, podemos estimar de la siguiente manera:

$$\sin\left(\dfrac{π}{18}\right)≈p_5\left(\dfrac{π}{18}\right)=\dfrac{π}{18}−\dfrac{1}{3!}\left(\dfrac{π}{18}\right)^3+\dfrac{1}{5!}\left(\dfrac{π}{18}\right)^5≈0.173648. \nonumber$$

Para estimar el error, use el hecho de que es el sexto polinomio Maclaurin$p_6(x)=p_5(x)$ y calcule un límite en$R_6(\dfrac{π}{18})$. Por Nota, el resto es

$$R_6\left(\dfrac{π}{18}\right)=\dfrac{f^{(7)}(c)}{7!}\left(\dfrac{π}{18}\right)^7 \nonumber$$

para algunos$c$ entre 0 y$\dfrac{π}{18}$. Utilizando el hecho de que$∣f^{(7)}(x)∣≤1$ para todos$x$, nos encontramos con que la magnitud del error es a lo sumo

$$\dfrac{1}{7!}⋅\left(\dfrac{π}{18}\right)^7≤9.8×10^{−10}. \nonumber$$

b.

Necesitamos encontrar los valores de$x$ tal que

$$\dfrac{1}{7!}|x|^7≤0.0001. \nonumber$$

Resolviendo esta desigualdad para$x$, tenemos que el quinto polinomio Maclaurin da una estimación a dentro$0.0001$ siempre y cuando$|x|<0.907.$

Ejercicio$\PageIndex{4}$

Usar el cuarto polinomio Maclaurin para$\cos x$ aproximar$\cos\left(\dfrac{π}{12}\right).$

Pista

El cuarto polinomio Maclaurin es$p_4(x)=1−\dfrac{x^2}{2!}+\dfrac{x^4}{4!}$.

Contestar

0.96593

Ahora que somos capaces de encuadernar el resto$R_n(x)$, podemos usar este límite para demostrar que una serie de Taylor para$f$ a converge a$f$.

Representando funciones con las series Taylor y Maclaurin

Ahora discutimos temas de convergencia para la serie Taylor. Comenzamos mostrando cómo encontrar una serie de Taylor para una función, y cómo encontrar su intervalo de convergencia.

Ejemplo$\PageIndex{5}$: Finding a Taylor Series

Encuentra la serie Taylor para$f(x)=\dfrac{1}{x}$ en$x=1$. Determinar el intervalo de convergencia.

Solución

Para$f(x)=\dfrac{1}{x},$ los valores de la función y sus primeras cuatro derivadas at$x=1$ son

\ [\ begin {alinear*} f (x) &=\ dfrac {1} {x} & f (1) &=1\\ [5pt]
f′ (x) &=−\ dfrac {1} {x^2} & f′ (1) &=−1\\ [5pt]
f "(x) &=\ dfrac {2} {x^3} & f" (1) &=2! \\ [5pt]
f"' (x) &=−\ dfrac {32} {x^4} & f"' (1) &=−3! \\ [5pt]
f^ {(4)} (x) &=\ dfrac {432} {x^5} & f^ {(4)} (1) &=4!. \ end {alinear*}\]

Es decir, tenemos$f^{(n)}(1)=(−1)^nn!$ para todos$n≥0$. Por lo tanto, la serie Taylor para$f$ at$x=1$ está dada por

$\displaystyle \sum_{n=0}^∞\dfrac{f^{(n)}(1)}{n!}(x−1)^n=\sum_{n=0}^∞(−1)^n(x−1)^n$.

Para encontrar el intervalo de convergencia, utilizamos la prueba de ratio. Nos encontramos con que

$\dfrac{|a_{n+1}|}{|a_n|}=\dfrac{∣(−1)^{n+1}(x−1)n^{+1}∣}{|(−1)^n(x−1)^n|}=|x−1|$.

Así, la serie converge si$|x−1|<1.$ Eso es, la serie converge para$0<x<2$. A continuación, tenemos que verificar los puntos finales. En$x=2$, vemos que

$\displaystyle \sum_{n=0}^∞(−1)^n(2−1)^n=\sum_{n=0}^∞(−1)^n$

diverge por la prueba de divergencia. Del mismo modo, en$x=0,$

$\displaystyle \sum_{n=0}^∞(−1)^n(0−1)^n=\sum_{n=0}^∞(−1)^{2n}=\sum_{n=0}^∞1$

diverge. Por lo tanto, el intervalo de convergencia es$(0,2)$.

Ejercicio$\PageIndex{5}$

Encuentra la serie Taylor para$f(x)=\dfrac{1}{2}$ at$x=2$ y determina su intervalo de convergencia.

Pista

$f^{(n)}(2)=\dfrac{(−1)^nn!}{2^{n+1}}$

Contestar

$\dfrac{1}{2}\displaystyle \sum_{n=0}^∞\left(\dfrac{2−x}{2}\right)^n$. El intervalo de convergencia es$(0,4)$.

Sabemos que la serie Taylor que se encuentra en este ejemplo converge en el intervalo$(0,2)$, pero ¿cómo sabemos que realmente converge a$f$? Consideramos esta pregunta con más generalidad en un momento, pero para este ejemplo, podemos responder a esta pregunta escribiendo

$$f(x)=\dfrac{1}{x}=\dfrac{1}{1−(1−x)}. \nonumber$$

Es decir,$f$ puede ser representado por la serie geométrica$\displaystyle \sum_{n=0}^∞(1−x)^n$. Dado que se trata de una serie geométrica, converge hasta$\dfrac{1}{x}$ siempre y cuando$|1−x|<1.$ Por lo tanto, la serie Taylor que se encuentra en Example converge a$f(x)=\dfrac{1}{x}$ on$(0,2).$

Consideramos ahora la pregunta más general: si una serie de Taylor para una función$f$ converge en algún intervalo, ¿cómo podemos determinar si realmente converge a$f$? Para responder a esta pregunta, recordemos que una serie converge a un valor particular si y sólo si su secuencia de sumas parciales converge a ese valor. Dada una serie de Taylor para$f$ at$a$, la suma$n^{\text{th}}$ parcial viene dada por el polinomio de Taylor$n^{\text{th}}$ -grado$p_n$. Por lo tanto, para determinar si la serie Taylor converge a$f$, necesitamos determinar si

$\displaystyle \lim_{n→∞}p_n(x)=f(x)$.

Desde el resto$R_n(x)=f(x)−p_n(x)$, la serie Taylor converge a$f$ si y solo si

$\displaystyle \lim_{n→∞}R_n(x)=0.$

Ahora declaramos este teorema formalmente.

Convergencia de la serie Taylor

Supongamos que$f$ tiene derivadas de todos los órdenes en un intervalo$I$ que contiene$a$. Luego la serie Taylor

$$\sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n \nonumber$$

converge a$f(x)$ para todos$x$ en$I$ si y solo si

$$\lim_{n→∞}R_n(x)=0 \nonumber$$

para todos$x$ en$I$.

Con este teorema, podemos probar que una serie de Taylor para$f$ a un converge a$f$ si podemos probar que el resto$R_n(x)→0$. Para probarlo$R_n(x)→0$, normalmente usamos el límite

$$|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber$$

del teorema de Taylor con resto.

En el siguiente ejemplo, encontramos la serie Maclaurin para$e^x$ y$\sin x$ y mostramos que estas series convergen a las funciones correspondientes para todos los números reales al demostrar que los restos$R_n(x)→0$ para todos los números reales$x$.

Ejemplo$\PageIndex{6}$: Finding Maclaurin Series

Para cada una de las siguientes funciones, encuentra la serie Maclaurin y su intervalo de convergencia. Use Note para probar que la serie Maclaurin para$f$ converge$f$ en ese intervalo.

1. $e^x$
2. $\sin x$

Solución

a. Usando el polinomio$n^{\text{th}}$ -grado Maclaurin para$e^x$ encontrado en el Ejemplo a., encontramos que la serie Maclaurin para$e^x$ viene dada por

$\displaystyle \sum_{n=0}^∞\dfrac{x^n}{n!}$.

Para determinar el intervalo de convergencia, utilizamos la prueba de ratio. Desde

$\dfrac{|a_{n+1}|}{|a_n|}=\dfrac{|x|^{n+1}}{(n+1)!}⋅\dfrac{n!}{|x|^n}=\dfrac{|x|}{n+1}$,

tenemos

$\displaystyle \lim_{n→∞}\dfrac{|a_{n+1}|}{|a_n|}=\lim_{n→∞}\dfrac{|x|}{n+1}=0$

para todos$x$. Por lo tanto, la serie converge absolutamente para todos$x$, y así, el intervalo de convergencia es$(−∞,∞)$. Para demostrar que la serie converge$e^x$ para todos$x$, utilizamos el hecho de que$f^{(n)}(x)=e^x$ para todos$n≥0$ y$e^x$ es una función cada vez mayor en$(−∞,∞)$. Por lo tanto, para cualquier número real$b$, el valor máximo de$e^x$ para todos$|x|≤b$ es$e^b$. Por lo tanto,

$|R_n(x)|≤\dfrac{e^b}{(n+1)!}|x|^{n+1}$.

Ya que acabamos de mostrar que

$\displaystyle \sum_{n=0}^∞\dfrac{|x|^n}{n!}$

converge para todos$x$, por la prueba de divergencia, sabemos que

$\displaystyle \lim_{n→∞}\dfrac{|x|^{n+1}}{(n+1)!}=0$

para cualquier número real$x$. Al combinar este hecho con el teorema squeeze, el resultado es$\displaystyle \lim_{n→∞}R_n(x)=0.$

b. Usando el polinomio$n^{\text{th}}$ -grado Maclaurin para$\sin x$ encontrado en el Ejemplo b., encontramos que la serie Maclaurin para$\sin x$ viene dada por

$\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n+1}}{(2n+1)!}$.

Para aplicar la prueba de relación, considere

\ [\ begin {alinear*}\ dfrac {|a_ {n+1} |} {|a_n|} &=\ dfrac {|x|^ {2n+3}} {(2n+3)!} ⋅\ dfrac {(2n+1)!} {|x|^ {2n+1}}\\ [5pt]
&=\ dfrac {|x|^2} {(2n+3) (2n+2)}\ end {align*}. \ nonumber\]

Desde

$\displaystyle \lim_{n→∞}\dfrac{|x|^2}{(2n+3)(2n+2)}=0$

para todos$x$, obtenemos el intervalo de convergencia como$(−∞,∞).$ Para mostrar que la serie Maclaurin converge a$\sin x$, mirar$R_n(x)$. Para cada uno$x$ existe un número real$c$ entre$0$ y$x$ tal que

$R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}x^{n+1}$.

Ya que$∣f^{(n+1)}(c)∣≤1$ para todos los números enteros$n$ y todos los números reales $c$, tenemos

$|R_n(x)|≤\dfrac{|x|^{n+1}}{(n+1)!}$

para todos los números reales$x$. Usando la misma idea que en la parte a., el resultado es$\displaystyle \lim_{n→∞}R_n(x)=0$ para todos$x$, y por lo tanto, la serie Maclaurin para$\sin x$ converge a$\sin x$ para todos reales$x$.

Ejercicio$\PageIndex{6}$

Encuentra la serie Maclaurin para$f(x)=\cos x$. Utilice la prueba de ratio para mostrar que el intervalo de convergencia es$(−∞,∞)$. Demuestre que la serie Maclaurin converge$\cos x$ para todos los números reales$x$.

Pista

Utilice los polinomios de Maclaurin para$\cos x.$

Contestar

$\displaystyle \sum_{n=0}^∞\dfrac{(−1)^nx^{2n}}{(2n)!}$

Por la prueba de ratio, el intervalo de convergencia es$(−∞,∞).$ Desde$|R_n(x)|≤\dfrac{|x|^{n+1}}{(n+1)!}$, la serie converge a$\cos x$ para todos los reales$x$.

Demostrando que$e$ is Irrational

En este proyecto, utilizamos los polinomios de Maclaurin$e^x$ para demostrar que$e$ es irracional. La prueba se basa en suponer que eso$e$ es racional y llegar a una contradicción. Por lo tanto, en los siguientes pasos, suponemos$e=r/s$ para algunos enteros$r$ y$s$ donde$s≠0.$

1. Escribe los polinomios Maclaurin$p_0(x),p_1(x),p_2(x),p_3(x),p_4(x)$ para$e^x$. $p_0(1),p_1(1),p_2(1),p_3(1),p_4(1)$Evaluar para estimar$e$.
2. Dejar$R_n(x)$ denotar el resto cuando se utiliza$p_n(x)$ para estimar$e^x$. Por lo tanto$R_n(x)=e^x−p_n(x)$,, y$R_n(1)=e−p_n(1)$. Suponiendo que$e=\dfrac{r}{s}$ para los enteros$r$ y$s$, evaluar$R_0(1),R_1(1),R_2(1),R_3(1),R_4(1).$
3. Usando los resultados de la parte 2, muestran que por cada resto$R_0(1),R_1(1),R_2(1),R_3(1),R_4(1),$ podemos encontrar un entero$k$ tal que$kR_n(1)$ sea un entero para$n=0,1,2,3,4.$
4. Anote la fórmula para el polinomio de Maclaurin$n^{\text{th}}$ -grado$p_n(x)$ para$e^x$ y el resto correspondiente$R_n(x).$ Mostrar que$sn!R_n(1)$ es un entero.
5. Usa el teorema de Taylor para escribir una fórmula explícita para$R_n(1)$. Concluir que$R_n(1)≠0$, y por lo tanto,$sn!R_n(1)≠0$.
6. Utilice el teorema de Taylor para encontrar una estimación sobre$R_n(1)$. Utilice esta estimación combinada con el resultado de la parte 5 para demostrarlo$|sn!R_n(1)|<\dfrac{se}{n+1}$. Concluir que si$n$ es lo suficientemente grande, entonces$|sn!R_n(1)|<1$. Por lo tanto,$sn!R_n(1)$ es un número entero con magnitud menor a 1. Así,$sn!R_n(1)=0$. Pero a partir de la parte 5, eso lo sabemos$sn!R_n(1)≠0$. Hemos llegado a una contradicción, y en consecuencia, la suposición original de que e es racional debe ser falsa.

Conceptos clave

• Los polinomios de Taylor se utilizan para aproximar funciones cercanas a un valor$x=a$. Los polinomios de Maclaurin son polinomios de Taylor en$x=0$.
• Los polinomios de Taylor de$n^{\text{th}}$ grado para una función$f$ son las sumas parciales de la serie Taylor para$f$.
• Si una función$f$ tiene una representación de serie de potencia en$x=a$, entonces es dada por su serie Taylor en$x=a$.
• Una serie Taylor para$f$ converge a$f$ si y solo si$\displaystyle \lim_{n→∞}R_n(x)=0$ donde$R_n(x)=f(x)−p_n(x)$.
• La serie Taylor para$e^x, \sin x$, y$\cos x$ convergen a las funciones respectivas para todos x reales.

Ecuaciones Clave

• Serie Taylor para la función$f$ en el punto$x=a$

$\displaystyle \sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n+⋯$

Glosario

Polinomio Maclaurin

un polinomio de Taylor centrado en$0$; el polinomio de Taylor de$n^{\text{th}}$ -grado para$f$ at$0$ es el polinomio de Maclaurin de$n^{\text{th}}$ grado para$f$

Serie Maclaurin

una serie de Taylor para una función$f$ en$x=0$ se conoce como una serie de Maclaurin para$f$

Polinomios de Taylor

el polinomio de$n^{\text{th}}$ grado Taylor para$f$ at$x=a$ es$p_n(x)=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n$

Serie Taylor

una serie de potencia en$a$ que converge a una función$f$ en algún intervalo abierto que contiene$a$.

Teorema de Taylor con resto

para una función$f$ y el polinomio de Taylor$n^{\text{th}}$ -grado para$f$ at$x=a$, el resto$R_n(x)=f(x)−p_n(x)$ satisface$R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1}$

para algunos$c$ entre$x$ y$a$; si existe un intervalo$I$ que contiene$a$ y un número real$M$ tal que$∣f^{(n+1)}(x)∣≤M$ para todos$x$ en$I$, entonces$|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1}$