10.3E: Ejercicios para la Sección 10.3

Polinomios de Taylor

En los ejercicios 1 - 8, se encuentran los polinomios Taylor de grado dos aproximándose a la función dada centrada en el punto dado.

1)\( f(x)=1+x+x^2\) en\( a=1\)

2)\( f(x)=1+x+x^2\) en\( a=−1\)

Contestar

\( f(−1)=1;\;f′(−1)=−1;\;f''(−1)=2;\quad p_2(x)=1−(x+1)+(x+1)^2\)

3)\( f(x)=\cos(2x)\) en\( a=π\)

4)\( f(x)=\sin(2x)\) en\( a=\frac{π}{2}\)

Contestar

\( f′(x)=2\cos(2x);\;f''(x)=−4\sin(2x);\quad p_2(x)=−2(x−\frac{π}{2})\)

5)\( f(x)=\sqrt{x}\) en\( a=4\)

6)\( f(x)=\ln x\) en\( a=1\)

Contestar

\( f′(x)=\dfrac{1}{x};\; f''(x)=−\dfrac{1}{x^2};\quad p_2(x)=0+(x−1)−\frac{1}{2}(x−1)^2\)

7)\( f(x)=\dfrac{1}{x}\) en\( a=1\)

8)\( f(x)=e^x\) en\( a=1\)

Contestar

\( p_2(x)=e+e(x−1)+\dfrac{e}{2}(x−1)^2\)

Teorema del resto de Taylor

En los ejercicios 9 - 14, verificar que la elección dada de\(n\) en la estimación restante\( |R_n|≤\dfrac{M}{(n+1)!}(x−a)^{n+1}\), donde\(M\) está el valor máximo de\( ∣f^{(n+1)}(z)∣\) en el intervalo entre\(a\) y el punto indicado, rinde\( |R_n|≤\frac{1}{1000}\). Encuentra el valor del polinomio Taylor\( p_n\) de\( f\) en el punto indicado.

9) [T]\( \sqrt{10};\; a=9,\; n=3\)

10) [T]\( (28)^{1/3};\; a=27,\; n=1\)

Contestar

\( \dfrac{d^2}{dx^2}x^{1/3}=−\dfrac{2}{9x^{5/3}}≥−0.00092…\)cuando\( x≥28\) así la estimación del resto se aplica a la aproximación lineal\( x^{1/3}≈p_1(27)=3+\dfrac{x−27}{27}\), lo que da\( (28)^{1/3}≈3+\frac{1}{27}=3.\bar{037}\), mientras que\( (28)^{1/3}≈3.03658.\)

11) [T]\( \sin(6);\; a=2π,\; n=5\)

12) [T]\( e^2; \; a=0,\; n=9\)

Contestar

Usando la estimación\( \dfrac{2^{10}}{10!}<0.000283\) podemos utilizar la expansión Taylor del orden 9 para estimar\( e^x\) en\( x=2\). como\( e^2≈p_9(2)=1+2+\frac{2^2}{2}+\frac{2^3}{6}+⋯+\frac{2^9}{9!}=7.3887\)... mientras que\( e^2≈7.3891.\)

13) [T]\( \cos(\frac{π}{5});\; a=0,\; n=4\)

14) [T]\( \ln(2);\; a=1,\; n=1000\)

Contestar

Ya que\( \dfrac{d^n}{dx^n}(\ln x)=(−1)^{n−1}\dfrac{(n−1)!}{x^n},R_{1000}≈\frac{1}{1001}\). Uno tiene\(\displaystyle p_{1000}(1)=\sum_{n=1}^{1000}\dfrac{(−1)^{n−1}}{n}≈0.6936\) mientras\( \ln(2)≈0.6931⋯.\)

Aproximación de integrales definidas usando la serie Taylor

15) Integrar la aproximación\(\sin t≈t−\dfrac{t^3}{6}+\dfrac{t^5}{120}−\dfrac{t^7}{5040}\) evaluada a\( π\) t a aproximada\(\displaystyle ∫^1_0\frac{\sin πt}{πt}\,dt\).

16) Integrar la aproximación\( e^x≈1+x+\dfrac{x^2}{2}+⋯+\dfrac{x^6}{720}\) evaluada\( −x^2\) a aproximada\(\displaystyle ∫^1_0e^{−x^2}\,dx.\)

Contestar

\(\displaystyle ∫^1_0\left(1−x^2+\frac{x^4}{2}−\frac{x^6}{6}+\frac{x^8}{24}−\frac{x^{10}}{120}+\frac{x^{12}}{720}\right)\,dx =1−\frac{1^3}{3}+\frac{1^5}{10}−\frac{1^7}{42}+\frac{1^9}{9⋅24}−\frac{1^{11}}{120⋅11}+\frac{1^{13}}{720⋅13}≈0.74683\)mientras que\(\displaystyle ∫^1_0e^{−x^2}dx≈0.74682.\)

Más problemas del teorema del resto de Taylor

En los ejercicios 17 - 20, encuentra el valor más pequeño de\(n\) tal manera que la estimación del resto\( |R_n|≤\dfrac{M}{(n+1)!}(x−a)^{n+1}\), donde\(M\) está el valor máximo de\( ∣f^{(n+1)}(z)∣\) en el intervalo entre\(a\) y el punto indicado, rinde\( |R_n|≤\frac{1}{1000}\) sobre el intervalo indicado.

17)\( f(x)=\sin x\) en\( [−π,π],\; a=0\)

18)\( f(x)=\cos x\) en\( [−\frac{π}{2},\frac{π}{2}],\; a=0\)

Contestar

Ya que\( f^{(n+1)}(z)\) es\(\sin z\) o\(\cos z\), tenemos\( M=1\). Ya que\( |x−0|≤\frac{π}{2}\), buscamos los más pequeños de\(n\) tal manera que\( \dfrac{π^{n+1}}{2^{n+1}(n+1)!}≤0.001\). El menor tal valor es\( n=7\). La estimación del resto es\( R_7≤0.00092.\)

19)\( f(x)=e^{−2x}\) en\( [−1,1],a=0\)

20)\( f(x)=e^{−x}\) en\( [−3,3],a=0\)

Responder

Ya que\( f^{(n+1)}(z)=±e^{−z}\) uno tiene\( M=e^3\). Ya que\( |x−0|≤3\), se busca el más pequeño\(n\) tal que\( \dfrac{3^{n+1}e^3}{(n+1)!}≤0.001\). El menor tal valor es\( n=14\). La estimación del resto es\( R_{14}≤0.000220.\)

En los ejercicios 21 - 24, el máximo del lado derecho de la estimación del resto\( |R_1|≤\dfrac{max|f''(z)|}{2}R^2\) en\( [a−R,a+R]\) ocurre en\(a\) o\( a±R\). Estimar el valor máximo de\(R\) tal que\( \dfrac{max|f''(z)|}{2}R^2≤0.1\) en\( [a−R,a+R]\) trazando este máximo en función de\(R\).

21) [T]\( e^x\) aproximado por\( 1+x,\; a=0\)

22) [T]\( \sin x\) aproximado por\( x,\; a=0\)

Responder

Ya que\( \sin x\) está aumentando para pequeños\( x\) y desde entonces\( \frac{d^2}{dx^2}\left(\sin x\right)=−\sin x\), la estimación se aplica siempre\( R^2\sin(R)≤0.2\), que aplica hasta\( R=0.596.\)

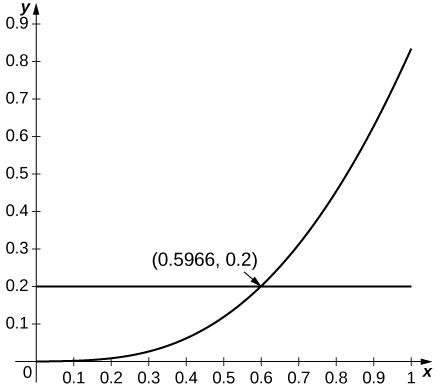
23) [T]\( \ln x\) aproximado por\( x−1,\; a=1\)

24) [T]\( \cos x\) aproximado por\( 1,\; a=0\)

Responder

Dado que la segunda derivada de\( \cos x\) es\( −\cos x\) y desde\( \cos x\) está disminuyendo alejándose de\( x=0\), la estimación se aplica cuando\( R^2\cos R≤0.2\) o\( R≤0.447\).

Serie Taylor

En los ejercicios 25 - 35, encuentra la serie Taylor de la función dada centrada en el punto indicado.

25)\(f(x) = x^4\) en\( a=−1\)

26)\(f(x) = 1+x+x^2+x^3\) en\( a=−1\)

Responder

\( (x+1)^3−2(x+1)^2+2(x+1)\)

27)\(f(x) = \sin x\) en\( a=π\)

28)\(f(x) = \cos x\) en\( a=2π\)

Responder

Los valores de los derivados son los mismos\( x=0\) que para\(\displaystyle \cos x=\sum_{n=0}^∞(−1)^n\frac{(x−2π)^{2n}}{(2n)!}\)

29)\(f(x) = \sin x\) en\( x=\frac{π}{2}\)

30)\(f(x) = \cos x\) en\( x=\frac{π}{2}\)

Responder

\( \cos(\frac{π}{2})=0,\;−\sin(\frac{π}{2})=−1\)entonces\(\displaystyle \cos x=\sum_{n=0}^∞(−1)^{n+1}\frac{(x−\frac{π}{2})^{2n+1}}{(2n+1)!}\), que es también\( −\cos(x−\frac{π}{2})\).

31)\(f(x) = e^x\) en\( a=−1\)

32)\(f(x) = e^x\) en\( a=1\)

Responder

Los derivados son\( f^{(n)}(1)=e,\) tan\(\displaystyle e^x=e\sum_{n=0}^∞\frac{(x−1)^n}{n!}.\)

33)\(f(x) = \dfrac{1}{(x−1)^2}\) en\( a=0\) (Pista: Diferenciar la serie Taylor para\( \dfrac{1}{1−x}\).)

34)\(f(x) = \dfrac{1}{(x−1)^3}\) en\( a=0\)

Responder

\(\displaystyle \frac{1}{(x−1)^3}=−\frac{1}{2}\frac{d^2}{dx^2}\left(\frac{1}{1−x}\right)=−\sum_{n=0}^∞\left(\frac{(n+2)(n+1)x^n}{2}\right)\)

35)\(\displaystyle F(x)=∫^x_0\cos(\sqrt{t})\,dt;\quad \text{where}\; f(t)=\sum_{n=0}^∞(−1)^n\frac{t^n}{(2n)!}\) a a=0 (Nota:\( f\) es la serie Taylor de\(\cos(\sqrt{t}).)\)

En los ejercicios 36 - 44, computa la serie Taylor de cada función alrededor\( x=1\).

36)\( f(x)=2−x\)

Responder

\( 2−x=1−(x−1)\)

37)\( f(x)=x^3\)

38)\( f(x)=(x−2)^2\)

Responder

\( ((x−1)−1)^2=(x−1)^2−2(x−1)+1\)

39)\( f(x)=\ln x\)

40)\( f(x)=\dfrac{1}{x}\)

Responder

\(\displaystyle \frac{1}{1−(1−x)}=\sum_{n=0}^∞(−1)^n(x−1)^n\)

41)\( f(x)=\dfrac{1}{2x−x^2}\)

42)\( f(x)=\dfrac{x}{4x−2x^2−1}\)

Responder

\(\displaystyle x\sum_{n=0}^∞2^n(1−x)^{2n}=\sum_{n=0}^∞2^n(x−1)^{2n+1}+\sum_{n=0}^∞2^n(x−1)^{2n}\)

43)\( f(x)=e^{−x}\)

44)\( f(x)=e^{2x}\)

Responder

\(\displaystyle e^{2x}=e^{2(x−1)+2}=e^2\sum_{n=0}^∞\frac{2^n(x−1)^n}{n!}\)

Serie Maclaurin

[T] En los ejercicios 45 - 48, identificar el valor de\(x\) tal que la serie dada\(\displaystyle \sum_{n=0}^∞a_n\) es el valor de la serie Maclaurin de\( f(x)\) at\( x\). Aproximar el valor de\( f(x)\) usar\(\displaystyle S_{10}=\sum_{n=0}^{10}a_n\).

45)\(\displaystyle \sum_{n=0}^∞\frac{1}{n!}\)

46)\(\displaystyle \sum_{n=0}^∞\frac{2^n}{n!}\)

Responder

\( x=e^2;\quad S_{10}=\dfrac{34,913}{4725}≈7.3889947\)

47)\(\displaystyle \sum_{n=0}^∞\frac{(−1)^n(2π)^{2n}}{(2n)!}\)

48)\(\displaystyle \sum_{n=0}^∞\frac{(−1)^n(2π)^{2n+1}}{(2n+1)!}\)

Responder

\(\sin(2π)=0;\quad S_{10}=8.27×10^{−5}\)

En los ejercicios 49 - 52 utilizar las funciones\( S_5(x)=x−\dfrac{x^3}{6}+\dfrac{x^5}{120}\) y\( C_4(x)=1−\dfrac{x^2}{2}+\dfrac{x^4}{24}\) en\( [−π,π]\).

49) [T] Parcela\(\sin^2x−(S_5(x))^2\) en\( [−π,π]\). Compara la diferencia máxima con el cuadrado de la estimación del resto de Taylor para\( \sin x.\)

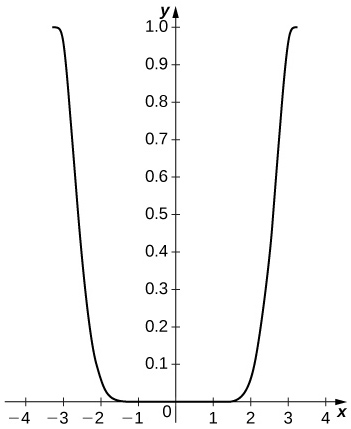
50) [T] Parcela\(\cos^2x−(C_4(x))^2\) en\( [−π,π]\). Compare la diferencia máxima con el cuadrado de la estimación del resto de Taylor para\( \cos x\).

Responder

La diferencia es pequeña en el interior del intervalo pero se acerca\( 1\) cerca de los puntos finales. La estimación del resto es\( |R_4|=\frac{π^5}{120}≈2.552.\)

51) [T] Parcela\( |2S_5(x)C_4(x)−\sin(2x)|\) en\( [−π,π]\).

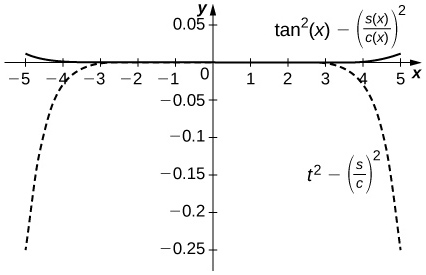
52) [T] Comparar\( \dfrac{S_5(x)}{C_4(x)}\)\( [−1,1]\) con\( \tan x\). Compare esto con la estimación del resto de Taylor para la aproximación de\( \tan x\) by\( x+\dfrac{x^3}{3}+\dfrac{2x^5}{15}\).

Responder

La diferencia está en el orden de\( 10^{−4}\) on\( [−1,1]\) mientras que el error de aproximación de Taylor está\( 0.1\) cerca\( ±1\). La curva superior es una gráfica de\(\tan^2x−\left(\dfrac{S_5(x)}{C_4(x)}\right)^2\) y la gráfica discontinua inferior se muestra\( t^2−\left(\dfrac{S_5}{C_4}\right)^2\).

53) [T] Parcela\( e^x−e_4(x)\) donde\( e_4(x)=1+x+\dfrac{x^2}{2}+\dfrac{x^3}{6}+\dfrac{x^4}{24}\) en\( [0,2]\). Compara el error máximo con la estimación del resto de Taylor.

54) (Aproximaciones de Taylor y hallazgo de raíz.) Recordemos que el método de Newton\( x_{n+1}=x_n−\dfrac{f(x_n)}{f'(x_n)}\) aproxima soluciones de\( f(x)=0\) cerca de la entrada\( x_0\).

a. si\( f\) y\( g\) son funciones inversas, explique por qué una solución de\( g(x)=a\) es el valor\( f(a)\) de\( f\).

b.\( p_N(x)\) Sea el\( N^{\text{th}}\) grado Maclaurin polinomio de\( e^x\). Utilice el método de Newton para aproximar soluciones de\( p_N(x)−2=0\) para\( N=4,5,6.\)

c. Explique por qué las raíces aproximadas de\( p_N(x)−2=0\) son valores aproximados de\(\ln(2).\)

Responder

a. Las respuestas variarán.
b. Los siguientes son los\( x_n\) valores después de\( 10\) iteraciones del método de Newton para aproximar una raíz de\( p_N(x)−2=0\): for\( N=4,x=0.6939...;\) for\( N=5,x=0.6932...;\) for\( N=6,x=0.69315...;.\) (Nota:\( \ln(2)=0.69314...\))
c. Las respuestas variarán.

Evaluar límites usando la serie Taylor

En los ejercicios 55 - 58, utilizar el hecho de que si\(\displaystyle q(x)=\sum_{n=1}^∞a_n(x−c)^n\) converge en un intervalo que contiene\( c\), entonces\(\displaystyle \lim_{x→c}q(x)=a_0\) para evaluar cada límite usando la serie Taylor.

55)\(\displaystyle \lim_{x→0}\frac{\cos x−1}{x^2}\)

56)\(\displaystyle \lim_{x→0}\frac{\ln(1−x^2)}{x^2}\)

Responder

\( \dfrac{\ln(1−x^2)}{x^2}→−1\)

57)\(\displaystyle \lim_{x→0}\frac{e^{x^2}−x^2−1}{x^4}\)

58)\(\displaystyle \lim_{x→0^+}\frac{\cos(\sqrt{x})−1}{2x}\)

Responder

\(\displaystyle \frac{\cos(\sqrt{x})−1}{2x}≈\frac{(1−\frac{x}{2}+\frac{x^2}{4!}−⋯)−1}{2x}→−\frac{1}{4}\)