10.1: Serie de potencia y funciones
- Page ID
- 116117
- Identifique una serie de potencias y proporcione ejemplos de ellas.
- Determinar el radio de convergencia y el intervalo de convergencia de una serie de potencias.
- Utilice una serie de potencia para representar una función.
Una serie de potencia es un tipo de serie con términos que involucran una variable. Más específicamente, si la variable es\(x\), entonces todos los términos de la serie involucran potencias de\(x\). Como resultado, una serie de poder puede ser pensada como un polinomio infinito. Las series de potencia se utilizan para representar funciones comunes y también para definir nuevas funciones. En esta sección definimos series de potencia y mostramos cómo determinar cuándo converge una serie de potencias y cuándo diverge. También mostramos cómo representar ciertas funciones usando series de potencia.
Forma de una serie de potencia
Una serie de la forma
\[\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+\ldots , \nonumber \]
donde\(x\) es una variable y los coeficientes\(c_n\) son constantes, se conoce como serie de potencia. La serie
\[1+x+x^2+\ldots =\sum_{n=0}^∞x^n \nonumber \]
es un ejemplo de una serie de potencia. Dado que esta serie es una serie geométrica con ratio\(r=|x|\), sabemos que converge si\(|x|<1\) y diverge si\(|x|≥1.\)
Una serie de la forma
\[\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+\ldots \nonumber \]
es una serie de potencia centrada en\(x=0.\) una serie de la forma
\[\sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(x−a)+c_2(x−a)^2+\ldots \nonumber \]
es una serie de potencia centrada en\(x=a\).
Para precisar esta definición, estipulamos eso\(x^0=1\) e\((x−a)^0=1\) incluso cuándo\(x=0\) y\(x=a\), respectivamente.
La serie
\[\sum_{n=0}^∞\dfrac{x^n}{n!}=1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\ldots \nonumber \]
y
\[\sum_{n=0}^∞n!x^n=1+x+2!x^2+3!x^3+\ldots \nonumber \]
están ambas series de potencia centradas en\(x=0.\) la serie
\[\sum_{n=0}^∞\dfrac{(x−2)^n}{(n+1)3^n}=1+\dfrac{x−2}{2⋅3}+\dfrac{(x−2)^2}{3⋅3^2}+\dfrac{(x−2)^3}{4⋅3^3}+\ldots \nonumber \]
es una serie de potencia centrada en\(x=2\).
Convergencia de una serie de potencia
Dado que los términos en una serie de potencias involucran una variable\(x\), la serie puede converger para ciertos valores de\(x\) y divergir para otros valores de\(x\). Para una serie de potencia centrada en\(x=a\), el valor de la serie at\(x=a\) viene dado por\(c_0\). Por lo tanto, una serie de potencia siempre converge en su centro. Algunas series de potencia convergen sólo a ese valor de\(x\). La mayoría de las series de potencia, sin embargo, convergen por más de un valor de\(x\). En ese caso, la serie de potencia o bien converge para todos los números reales\(x\) o converge para todos\(x\) en un intervalo finito. Por ejemplo, la serie geométrica\(\displaystyle \sum_{n=0}^∞x^n\) converge para todos\(x\) en el intervalo\((−1,1)\), pero diverge para todos\(x\) fuera de ese intervalo. Ahora resumimos estas tres posibilidades para una serie de potencia general.
Considere la serie de potencia\(\displaystyle \sum_{n=0}^∞c_n(x−a)^n.\) La serie satisface exactamente una de las siguientes propiedades:
- La serie converge\(x=a\) y diverge para todos\(x≠a.\)
- La serie converge para todos los números reales\(x\).
- Existe un número real\(R>0\) tal que la serie converge si\(|x−a|<R\) y diverge si\(|x−a|>R\). En los valores\(x\) donde |x−a|=R, la serie puede converger o divergir.
Supongamos que la serie de potencia está centrada en\(a=0\). (Para una serie centrada en un valor distinto de cero, el resultado sigue dejando\(y=x−a\) y considerando la serie
\[ \sum_{n=1}^∞c_ny^n. \nonumber \]
Primero debemos probar el siguiente hecho:
Si existe un número real\(d≠0\) tal que\(\displaystyle \sum_{n=0}^∞c_nd^n\) converja, entonces la serie\(\displaystyle \sum_{n=0}^∞c_nx^n\) converge absolutamente para todos\(x\) tal que\(|x|<|d|.\)
Ya que\(\displaystyle \sum_{n=0}^∞c_nd^n\) converge, el enésimo término\(c_nd^n→0\) como\(n→∞\). Por lo tanto, existe un entero\(N\) tal que\(|c_nd^n|≤1\) para todos los\(n≥N.\) Escritos
\[|c_nx^n|=|c_nd^n| \left|\dfrac{x}{d}\right|^n, \nonumber \]
concluimos que, para todos los N≥n,
\[|c_nx^n|≤\left|\dfrac{x}{d}\right|^n. \nonumber \]
La serie
\[\sum_{n=N}^∞\left|\dfrac{x}{d}\right|^n \nonumber \]
es una serie geométrica que converge si\(|\dfrac{x}{d}|<1.\) Por lo tanto, por la prueba de comparación, concluimos que\(\displaystyle \sum_{n=N}^∞c_nx^n\) también converge para\(|x|<|d|\). Como podemos agregar un número finito de términos a una serie convergente, concluimos que\(\displaystyle \sum_{n=0}^∞c_nx^n\) converge para\(|x|<|d|.\)
Con este resultado, ahora podemos probar el teorema. Considera la serie
\[\sum_{n=0}^∞a_nx^n \nonumber \]
y deja\(S\) ser el conjunto de números reales para los que converge la serie. Supongamos que el conjunto\(S={0}.\) Entonces la serie cae bajo el caso i.
Supongamos que el conjunto\(S\) es el conjunto de todos los números reales. Entonces la serie cae bajo el caso ii. Supongamos que\(S≠{0}\) y no\(S\) es el conjunto de números reales. Entonces existe un número real\(x*≠0\) tal que la serie no converge. Así, la serie no puede converger para ninguna\(x\) tal que\(|x|>|x*|\). Por lo tanto, el conjunto\(S\) debe ser un conjunto acotado, lo que significa que debe tener un límite superior más pequeño. (Este hecho se desprende de la Propiedad Límite Mínimo Superior para los números reales, que está más allá del alcance de este texto y se cubre en cursos de análisis real). Llama a ese límite superior más pequeño\(R\). Ya que\(S≠{0}\), el número\(R>0\). Por lo tanto, la serie converge para todos\(x\) tales que\(|x|<R,\) y la serie cae en el caso iii.
□
Si una serie\(\displaystyle \sum_{n=0}^∞c_n(x−a)^n\) cae en el caso iii. de Note, entonces la serie converge para todos\(x\) tal que\(|x−a|<R\) para algunos\(R>0\), y diverge para todos\(x\) tales que\(|x−a|>R\). La serie puede converger o divergir en los valores\(x\) donde\(|x−a|=R\). El conjunto de valores\(x\) para el que\(\displaystyle \sum_{n=0}^∞c_n(x−a)^n\) converge la serie se conoce como el intervalo de convergencia. Ya que la serie diverge para todos los valores\(x\) donde\(|x−a|>R\), la longitud del intervalo es\(2R\), y por lo tanto, el radio del intervalo es\(R\). El valor\(R\) se llama el radio de convergencia. Por ejemplo, ya que la serie\(\displaystyle \sum_{n=0}^∞x^n\) converge para todos los valores\(x\) en el intervalo\((−1,1)\) y diverge para todos los valores\(x\) tal que\(|x|≥1\), el intervalo de convergencia de esta serie es\((−1,1)\). Dado que la longitud del intervalo es\(2\), el radio de convergencia es\(1\).
Considera la serie Power\(\displaystyle \sum_{n=0}^∞c_n(x−a)^n\). El conjunto de números reales\(x\) donde converge la serie es el intervalo de convergencia. Si existe un número real\(R>0\) tal que la serie converge para\(|x−a|<R\) y diverge para\(|x−a|>R,\) entonces\(R\) es el radio de convergencia. Si la serie converge sólo en\(x=a\), decimos que el radio de convergencia es\(R=0\). Si la serie converge para todos los números reales\(x\), decimos que el radio de convergencia es\(R=∞\) (Figura\(\PageIndex{1}\)).
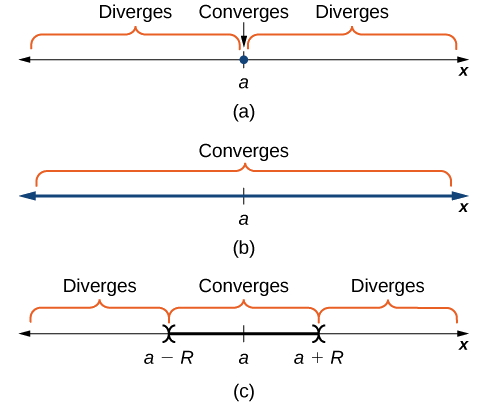
Para determinar el intervalo de convergencia para una serie de potencias, normalmente aplicamos la prueba de relación. En Ejemplo\(\PageIndex{1}\), mostramos las tres posibilidades diferentes ilustradas en la Figura\(\PageIndex{1}\).
Para cada una de las siguientes series, encuentre el intervalo y el radio de convergencia.
- \(\displaystyle \sum_{n=0}^∞\dfrac{x^n}{n!}\)
- \(\displaystyle \sum_{n=0}^∞n!x^n\)
- \(\displaystyle \sum_{n=0}^∞\dfrac{(x−2)^n}{(n+1)3^n}\)
Solución
a. Para verificar la convergencia, aplique la prueba de relación. Tenemos
\ [\ begin {alinear*} ρ &=\ lim_ {n→∞}\ izquierda|\ dfrac {\ dfrac {x^ {n+1}} {(n+1)!}} {\ dfrac {x^n} {n!}} \ derecha|\\ [4pt]
&=\ lim_ {n→∞}\ izquierda|\ dfrac {x^ {n+1}} {(n+1)!} ⋅\ dfrac {n!} {x^n}\ derecha|\\ [4pt]
&=\ lim_ {n→∞}\ izquierda|\ dfrac {x^ {n+1}} {(n+1) n!} ⋅\ dfrac {n!} {x^n}\ derecha|\\ [4pt]
&=\ lim_ {n→∞}\ izquierda|\ dfrac {x} {n+1}\ derecha|\\ [4pt]
&=|x|\ lim_ {n→∞}\ dfrac {1} {n+1}\\ [4pt]
&=0<1\ end {align*}\]
para todos los valores de\(x\). Por lo tanto, la serie converge para todos los números reales\(x\). El intervalo de convergencia es\((−∞,∞)\) y el radio de convergencia es\(R=∞.\)
b. Aplicar la prueba de relación. Para\(x≠0\), vemos que
\ [\ begin {align*} ρ &=\ lim_ {n→∞}\ izquierda|\ dfrac {(n+1)! x^ {n+1}} {n! x^n}\ derecha|\\ [4pt]
&=\ lim_ {n→∞} | (n+1) x|\\ [4pt]
&=|x|\ lim_ {n→∞} (n+1)\\ [4pt]
&=∞. \ end {alinear*}\]
Por lo tanto, la serie diverge para todos\(x≠0\). Dado que la serie está centrada en\(x=0\), debe converger ahí, por lo que la serie converge sólo para\(x≠0\). El intervalo de convergencia es el valor único\(x=0\) y el radio de convergencia es\(R=0\).
c. Para aplicar la prueba de relación, considere
\ [\ begin {align*} ρ &=\ lim_ {n→∞}\ izquierda|\ dfrac {\ dfrac {(x−2) ^ {n+1}} {(n+2) 3^ {n+1}}} {\ dfrac {(x−2) ^n} {(n+1) 3^n}}\ derecha|\\ [4pt]
&=\ lim_ _ {n→∞}\ izquierda|\ dfrac {(x−2) ^ {n+1}} {(n+2) 3^ {n+1}} ⋅\ dfrac {(n+1) 3^n} {(x−2) ^n}\ derecha|\\ [4pt]
&=\ lim_ {n→∞}\ izquierda|\ dfrac {(x−2) (n+1)} {3 (n+2)}\ derecha|\\ [4 pt]
&=\ dfrac {|x−2|} {3}. \ end {alinear*}\]
La relación\(ρ<1\) si\(|x−2|<3\). Ya que\(|x−2|<3\) implica que\(−3<x−2<3,\) la serie converge absolutamente si\(−1<x<5\). La relación\(ρ>1\) si\(|x−2|>3\). Por lo tanto, la serie diverge si\(x<−1\) o\(x>5\). La prueba de relación no es concluyente si\(ρ=1\). La relación\(ρ=1\) si y sólo si\(x=−1\) o\(x=5\). Necesitamos probar estos valores de\(x\) por separado. Para\(x=−1\), la serie viene dada por
\[ \sum_{n=0}^∞\dfrac{(−1)^n}{n+1}=1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+\ldots . \nonumber \]
Dado que esta es la serie armónica alterna, converge. Así, la serie converge en\(x=−1\). Para\(x=5\), la serie viene dada por
\[ \sum_{n=0}^∞\dfrac{1}{n+1}=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\ldots . \nonumber \]
Esta es la serie armónica, que es divergente. Por lo tanto, la serie de potencia diverge en\(x=5\). Concluimos que el intervalo de convergencia es\([−1,5)\) y el radio de convergencia es\(R=3\).
Encuentre el intervalo y el radio de convergencia para la serie
\[ \sum_{n=1}^∞\dfrac{x^n}{\sqrt{n}}. \nonumber \]
- Pista
-
Aplicar la prueba de relación para verificar la convergencia absoluta.
- Contestar
-
El intervalo de convergencia es\([−1,1).\) El radio de convergencia es\(R=1.\)
Representando funciones como serie de potencia
Ser capaz de representar una función mediante un “polinomio infinito” es una herramienta poderosa. Las funciones polinómicas son las funciones más fáciles de analizar, ya que solo involucran las operaciones aritméticas básicas de suma, resta, multiplicación y división. Si podemos representar una función complicada por un polinomio infinito, podemos usar la representación polinómica para diferenciarla o integrarla. Además, podemos usar una versión truncada de la expresión polinómica para aproximar valores de la función. Entonces, la pregunta es, ¿cuándo podemos representar una función por una serie de potencias?
Consideremos de nuevo la serie geométrica
\[1+x+x^2+x^3+\ldots =\sum_{n=0}^∞x^n. \nonumber \]
Recordemos que la serie geométrica
\[a+ar+ar^2+ar^3+\ldots \nonumber \]
converge si y sólo si\(|r|<1.\) En ese caso, converge a\(\dfrac{a}{1−r}\). Por lo tanto\(|x|<1\), si, la serie en Ejemplo\(\PageIndex{1}\) converge\(\dfrac{1}{1−x}\) y escribimos
\[1+x+x^2+x^3+\ldots =\dfrac{1}{1−x} for|x|<1. \nonumber \]
Como resultado, somos capaces de representar la función\(f(x)=\dfrac{1}{1−x}\) por la serie power
\[1+x+x^2+x^3+\ldots when|x|<1. \nonumber \]
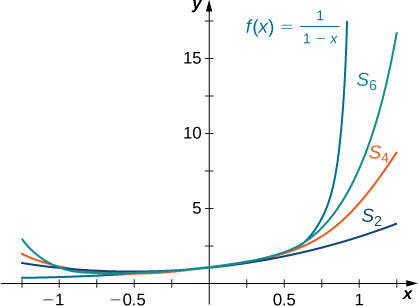
Ahora mostramos gráficamente cómo esta serie proporciona una representación para la función\(f(x)=\dfrac{1}{1−x}\) comparando la gráfica de\(f\) con las gráficas de varias de las sumas parciales de esta serie infinita.
Esboce una gráfica\(f(x)=\dfrac{1}{1−x}\) y las gráficas de las sumas parciales correspondientes\( \displaystyle S_N(x)=\sum_{n=0}^Nx^n\) para\(N=2,4,6\) en el intervalo\((−1,1)\). Comentar la aproximación a\(S_N\) medida que\(N\) aumenta.
Solución
De la gráfica de la Figura se ve que a medida que\(N\) aumenta,\(S_N\) se convierte en una mejor aproximación\(f(x)=\dfrac{1}{1−x}\) para para\(x\) en el intervalo\((−1,1)\).
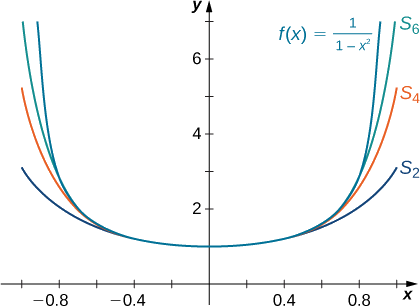
Esbozar una gráfica de\(f(x)=\dfrac{1}{1−x^2}\) y las sumas parciales correspondientes\(\displaystyle S_N(x)=\sum_{n=0}^Nx^{2n}\) para\(N=2,4,6\) en el intervalo\((−1,1).\)
- Pista
- \(S_N(x)=1+x^2+\ldots +x^{2N}=\dfrac{1−x^{2(N+1)}}{1−x^2}\)
- Contestar
-
A continuación consideramos funciones que involucran una expresión similar a la suma de una serie geométrica y mostramos cómo representar estas funciones usando series de potencia.
Utilice una serie de potencia para representar cada una de las siguientes funciones\(f\). Encuentra el intervalo de convergencia.
- \(f(x)=\dfrac{1}{1+x^3}\)
- \(f(x)=\dfrac{x^2}{4−x^2}\)
Solución
a. se debe reconocer esta función\(f\) como la suma de una serie geométrica, porque
\[ \dfrac{1}{1+x^3}=\dfrac{1}{1−(−x^3)}. \nonumber \]
Utilizando el hecho de que, para\(|r|<1,\dfrac{a}{1−r}\) es la suma de la serie geométrica
\[ \sum_{n=0}^∞ar^n=a+ar+ar^2+\ldots , \nonumber \]
vemos que, para\(|−x^3|<1,\)
\[ \begin{align*} \dfrac{1}{1+x^3} =\dfrac{1}{1−(−x^3)} \\[4pt] =\sum_{n=0}^∞(−x^3)^n \\[4pt] =1−x^3+x^6−x^9+\ldots . \end{align*}\]
Ya que esta serie converge si y solo si\(|−x^3|<1\), el intervalo de convergencia es\((−1,1)\), y tenemos
\[ \dfrac{1}{1+x^3}=1−x^3+x^6−x^9+\ldots for|x|<1.\nonumber \]
b. Esta función no está en la forma exacta de una suma de una serie geométrica. Sin embargo, con un poco de manipulación algebraica, podemos relacionar f con una serie geométrica. Al factorizar 4 de los dos términos en el denominador, obtenemos
\[ \begin{align*} \dfrac{x^2}{4−x^2} =\dfrac{x^2}{4(\dfrac{1−x^2}{4})}\\[4pt] =\dfrac{x^2}{4(1−(\dfrac{x}{2})^2)}.\end{align*}\]
Por lo tanto, tenemos
\ [\ begin {align*}\ dfrac {x^2} {4−x^2} &=\ dfrac {x^2} {4 (1− (\ dfrac {x} {2}) ^2)}\\ [4pt]
&=\ dfrac {\ dfrac {\ dfrac {x^2} {4}} {1− (\ dfrac {x} 2}) ^2}\\ [4pt]
&=\ suma_ {n=0} ^∞\ dfrac {x^2} {4} (\ dfrac {x} {2}) ^ {2n}. \ end {alinear*}\]
La serie converge siempre y cuando\(|(\dfrac{x}{2})^2|<1\) (tenga en cuenta que cuando\(|(\dfrac{x}{2})^2|=1\) la serie no converge). Resolviendo esta desigualdad, concluimos que el intervalo de convergencia es\((−2,2)\) y
\ [\ begin {align*}\ dfrac {x^2} {4−x^2} &=\ sum_ {n=0} ^∞\ dfrac {x^ {2n+2}} {4^ {n+1}}\\ [4pt]
&=\ dfrac {x^2} {4} +\ dfrac {x^4} {4^2} +\ dfrac {x^4} {4^2} +\ frac {x^6} {4^3} +\ ldots\ end {alinear*}\]
para\(|x|<2.\)
Representar la función\(f(x)=\dfrac{x^3}{2−x}\) usando una serie de potencias y encontrar el intervalo de convergencia.
- Pista
-
Reescribir f en la forma\(f(x)=\dfrac{g(x)}{1−h(x)}\) para algunas funciones\(g\) y\(h\).
- Responder
-
\(\displaystyle \sum_{n=0}^∞\dfrac{x^{n+3}}{2^{n+1}}\)con intervalo de convergencia\((−2,2)\)
En las secciones restantes de este capítulo, mostraremos formas de derivar representaciones de series de poder para muchas otras funciones, y cómo podemos hacer uso de estas representaciones para evaluar, diferenciar e integrar diversas funciones.
Conceptos clave
- Para una serie de potencia centrada en\(x=a\), se mantiene una de las siguientes tres propiedades:
- i. La serie power converge sólo en\(x=a\). En este caso, decimos que el radio de convergencia es\(R=0\).
- ii. La serie power converge para todos los números reales\(x\). En este caso, decimos que el radio de convergencia es\(R=∞\).
- iii. Hay un número real R tal que la serie converge para\(|x−a|<R\) y diverge para\(|x−a|>R\). En este caso, el radio de convergencia es\(R.\)
- Si una serie de potencia converge en un intervalo finito, la serie puede o no converger en los puntos finales.
- La prueba de relación a menudo se puede usar para determinar el radio de convergencia.
- La serie geométrica\(\displaystyle \sum_{n=0}^∞x^n=\dfrac{1}{1−x}\) para nos\(|x|<1\) permite representar ciertas funciones usando series geométricas.
Ecuaciones Clave
- Serie de potencia centrada en\(x=0\)
\[ \sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+\ldots n\nonumber \]
- Serie de potencia centrada en\(x=a\)
\[ \sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(x−a)+c_2(x−a)^2+\ldots \nonumber \]
Glosario
- intervalo de convergencia
- el conjunto de números reales\(x\) para los que converge una serie de potencia
- serie de potencia
- una serie de la forma\(\displaystyle \sum_{n=0}^∞c_nx^n\) es una serie de potencia centrada en\(x=0\); una serie de la forma\(\displaystyle \sum_{n=0}^∞c_n(x−a)^n\) es una serie de potencia centrada en\(x=a\)
- radio de convergencia
- si existe un número real\(R>0\) tal que una serie de potencia centrada en\(x=a\) converge\(|x−a|<R\) y diverge para\(|x−a|>R\), entonces\(R\) es el radio de convergencia; si la serie de potencia solo converge en\(x=a\), el radio de convergencia es\(R=0\); si la serie de potencia converge para todos los números reales\(x\), el radio de convergencia es\(R=∞\)