14.2E: Ejercicios para la Sección 14.2

1) Utilizar las leyes de límite para funciones de dos variables para evaluar cada límite a continuación, dado que$\displaystyle \lim_{(x,y)→(a,b)}f(x,y) = 5$ y$\displaystyle \lim_{(x,y)→(a,b)}g(x,y) = 2$.

1. $\displaystyle \lim_{(x,y)→(a,b)}\left[f(x,y) + g(x,y)\right]$
2. $\displaystyle \lim_{(x,y)→(a,b)}\left[f(x,y) g(x,y)\right]$
3. $\displaystyle \lim_{(x,y)→(a,b)}\left[ \dfrac{7f(x,y)}{g(x,y)}\right]$
4. $\displaystyle \lim_{(x,y)→(a,b)}\left[\dfrac{2f(x,y) - 4g(x,y)}{f(x,y) - g(x,y)}\right]$

Responder

1. $\displaystyle \lim_{(x,y)→(a,b)}\left[f(x,y) + g(x,y)\right] = \displaystyle \lim_{(x,y)→(a,b)}f(x,y) + \displaystyle \lim_{(x,y)→(a,b)}g(x,y)= 5 + 2 = 7$
2. $\displaystyle \lim_{(x,y)→(a,b)}\left[f(x,y) g(x,y)\right] =\left(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\right) \left(\displaystyle \lim_{(x,y)→(a,b)}g(x,y)\right) = 5(2) = 10$
3. $\displaystyle \lim_{(x,y)→(a,b)}\left[ \dfrac{7f(x,y)}{g(x,y)}\right] = \frac{7\left(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\right)}{\displaystyle \lim_{(x,y)→(a,b)}g(x,y)}=\frac{7(5)}{2} = 17.5$
4. $\displaystyle \lim_{(x,y)→(a,b)}\left[\dfrac{2f(x,y) - 4g(x,y)}{f(x,y) - g(x,y)}\right] = \frac{2\left(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\right) - 4 \left(\displaystyle \lim_{(x,y)→(a,b)}g(x,y)\right)}{\displaystyle \lim_{(x,y)→(a,b)}f(x,y) - \displaystyle \lim_{(x,y)→(a,b)}g(x,y)}= \frac{2(5) - 4(2)}{5 - 2} = \frac{2}{3}$

En los ejercicios 2 - 4, encuentra el límite de la función.

2)$\displaystyle \lim_{(x,y)→(1,2)}x$

3)$\displaystyle \lim_{(x,y)→(1,2)}\frac{5x^2y}{x^2+y^2}$

Responder

$\displaystyle \lim_{(x,y)→(1,2)}\frac{5x^2y}{x^2+y^2} = 2$

4) Mostrar que el límite$\displaystyle \lim_{(x,y)→(0,0)}\frac{5x^2y}{x^2+y^2}$ existe y es el mismo a lo largo de las trayectorias:$y$ -eje y$x$ -eje, y a lo largo$y=x$.

En los ejercicios 5 - 19, evaluar los límites a los valores indicados de$x$ y$y$. Si el límite no existe, indíquelo y explique por qué no existe el límite.

5)$\displaystyle \lim_{(x,y)→(0,0)}\frac{4x^2+10y^2+4}{4x^2−10y^2+6}$

Responder

$\displaystyle \lim_{(x,y)→(0,0)}\frac{4x^2+10y^2+4}{4x^2−10y^2+6} = \frac{2}{3}$

6)$\displaystyle \lim_{(x,y)→(11,13)}\sqrt{\frac{1}{xy}}$

7)$\displaystyle \lim_{(x,y)→(0,1)}\frac{y^2\sin x}{x}$

Responder

$\displaystyle \lim_{(x,y)→(0,1)}\frac{y^2\sin x}{x} = 1$

8)$\displaystyle \lim_{(x,y)→(0,0)}\sin(\frac{x^8+y^7}{x−y+10})$

9)$\displaystyle \lim_{(x,y)→(π/4,1)}\frac{y\tan x}{y+1}$

Responder

$\displaystyle \lim_{(x,y)→(π/4,1)}\frac{y\tan x}{y+1}=\frac{1}{2}$

10)$\displaystyle \lim_{(x,y)→(0,π/4)}\frac{\sec x+2}{3x−\tan y}$

11)$\displaystyle \lim_{(x,y)→(2,5)}(\frac{1}{x}−\frac{5}{y})$

Responder

$\displaystyle \lim_{(x,y)→(2,5)}(\frac{1}{x}−\frac{5}{y}) = −\frac{1}{2}$

12)$\displaystyle \lim_{(x,y)→(4,4)}x\ln y$

13)$\displaystyle \lim_{(x,y)→(4,4)}e^{−x^2−y^2}$

Responder

$\displaystyle \lim_{(x,y)→(4,4)}e^{−x^2−y^2} = e^{−32}$

14)$\displaystyle \lim_{(x,y)→(0,0)}\sqrt{9−x^2−y^2}$

15)$\displaystyle \lim_{(x,y)→(1,2)}(x^2y^3−x^3y^2+3x+2y)$

Responder

$\displaystyle \lim_{(x,y)→(1,2)}(x^2y^3−x^3y^2+3x+2y) = 11$

16)$\displaystyle \lim_{(x,y)→(π,π)}x\sin(\frac{x+y}{4})$

17)$\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+1}{x^2+y^2+1}$

Responder

$\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+1}{x^2+y^2+1} = 1$

18)$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2+y^2}{\sqrt{x^2+y^2+1}−1}$

19)$\displaystyle \lim_{(x,y)→(0,0)}\ln(x^2+y^2)$

Responder

El límite no existe porque cuando$x$ y$y$ ambos se acercan a cero, la función se acerca$\ln 0$, que es indefinida (se acerca al infinito negativo).

En los ejercicios 20 - 21, complete el enunciado.

20) Un punto$(x_0,y_0)$ en una región plana$R$ es un punto interior de$R$ si _________________.

21) Un punto$(x_0,y_0)$ en una región plana$R$ se denomina punto límite de$R$ si ___________.

Responder

Cada disco abierto centrado en$(x_0,y_0)$ contiene puntos dentro$R$ y fuera$R$.

En los ejercicios 22 - 25, utilizar técnicas algebraicas para evaluar el límite.

22)$\displaystyle \lim_{(x,y)→(2,1)}\frac{x−y−1}{\sqrt{x−y}−1}$

23)$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^4−4y^4}{x^2+2y^2}$

Responder

$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^4−4y^4}{x^2+2y^2} = 0$

24)$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^3−y^3}{x−y}$

25)$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2−xy}{\sqrt{x}−\sqrt{y}}$

Responder

$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2−xy}{\sqrt{x}−\sqrt{y}} = 0$

En los ejercicios 26 - 27, evaluar los límites de las funciones de tres variables.

26)$\displaystyle \lim_{(x,y,z)→(1,2,3)}\frac{xz^2−y^2z}{xyz−1}$

27)$\displaystyle \lim_{(x,y,z)→(0,0,0)}\frac{x^2−y^2−z^2}{x^2+y^2−z^2}$

Responder

El límite no existe.

En los ejercicios 28 - 31, evaluar el límite de la función determinando el valor que la función se aproxima a lo largo de los caminos indicados. Si el límite no existe, explique por qué no.

28)$\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+y^3}{x^2+y^2}$

a. A lo largo del$x$ eje$(y=0)$

b. A lo largo del$y$ eje$(x=0)$

c. A lo largo del camino$y=2x$

29) Evaluar$\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+y^3}{x^2+y^2}$ utilizando los resultados del problema anterior.

Responder

El límite no existe. La función se acerca a dos valores diferentes a lo largo de diferentes caminos.

30)$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2y}{x^4+y^2}$

a. A lo largo del$x$ eje$(y=0)$

b. A lo largo del$y$ eje$(x=0)$

c. A lo largo del camino$y=x^2$

31) Evaluar$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2y}{x^4+y^2}$ utilizando los resultados del problema anterior.

Responder

El límite no existe porque la función se acerca a dos valores diferentes a lo largo de los caminos.

En los ejercicios 32 - 35, discutir la continuidad de cada función. Encuentra la región más grande en el$xy$ plano -en el que cada función es continua.

32)$f(x,y)=\sin(xy)$

33)$f(x,y)=\ln(x+y)$

Responder

La función$f$ es continua en la región$y>−x.$

34)$f(x,y)=e^{3xy}$

35)$f(x,y)=\dfrac{1}{xy}$

Responder

La función$f$ es continua en todos los puntos del$xy$ plano, excepto en los puntos de los$y$ ejes$x$ - y -.

En los ejercicios 36 - 38, determinar la región en la que la función es continua. Explica tu respuesta.

36)$f(x,y)=\dfrac{x^2y}{x^2+y^2}$

37)$f(x,y)=$$\begin{cases}\dfrac{x^2y}{x^2+y^2} & if(x,y)≠(0,0)\\0 & if(x,y)=(0,0)\end{cases}$

Pista:

Mostrar que la función se acerca a diferentes valores a lo largo de dos caminos diferentes.

Responder

La función es continua en$(0,0)$ ya que el límite de la función at$(0,0)$ es$0$, el mismo valor de$f(0,0).$

38)$f(x,y)=\dfrac{\sin(x^2+y^2)}{x^2+y^2}$

39) Determinar si$g(x,y)=\dfrac{x^2−y^2}{x^2+y^2}$ es continuo en$(0,0)$.

Responder

La función es discontinua en$(0,0).$ El límite$(0,0)$ en no existe y$g(0,0)$ no existe.

40) Crear una gráfica utilizando software de gráficos para determinar dónde no existe el límite. Determinar la región del plano de coordenadas en la que$f(x,y)=\dfrac{1}{x^2−y}$ es continuo.

41) Determinar la región del$xy$ -plano en la que la función compuesta$g(x,y)=\arctan(\frac{xy^2}{x+y})$ es continua. Usa la tecnología para apoyar tu conclusión.

Responder

Dado que la función$\arctan x$ es continua sobre$(−∞,∞), g(x,y)=\arctan(\frac{xy^2}{x+y})$ es continua donde$z=\dfrac{xy^2}{x+y}$ es continua. La función interna$z$ es continua en todos los puntos del$xy$ plano -excepto donde$y=−x.$ Así,$g(x,y)=\arctan(\frac{xy^2}{x+y})$ es continua en todos los puntos del plano de coordenadas excepto en los puntos en los que$y=−x.$

42) Determinar la región del$xy$ -plano en el que$f(x,y)=\ln(x^2+y^2−1)$ es continuo. Usa la tecnología para apoyar tu conclusión. (Pista: ¡Elige el rango de valores para$x$ y$y$ con cuidado!)

43) ¿En qué puntos del espacio es$g(x,y,z)=x^2+y^2−2z^2$ continuo?

Responder

Todos los puntos$P(x,y,z)$ en el espacio

44) ¿En qué puntos del espacio es$g(x,y,z)=\dfrac{1}{x^2+z^2−1}$ continuo?

45) Mostrar que$\displaystyle \lim_{(x,y)→(0,0)}\frac{1}{x^2+y^2}$ no existe en$(0,0)$ trazando la gráfica de la función.

Responder

La gráfica aumenta sin límite como$x$ y$y$ ambos se acercan a cero.

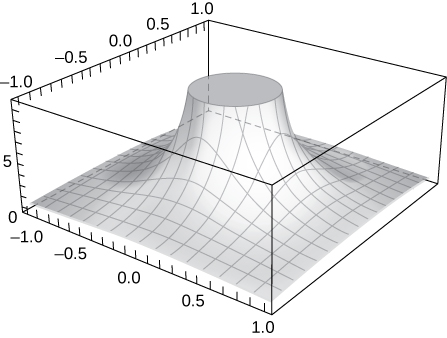
46) [T] Evaluar$\displaystyle \lim_{(x,y)→(0,0)}\frac{−xy^2}{x^2+y^4}$ trazando la función usando un CAS. Determinar analíticamente el límite a lo largo de la trayectoria$x=y^2.$

47) [T]

a. Utilice un CAS para dibujar un mapa de contorno de$z=\sqrt{9−x^2−y^2}$.

b. ¿Cuál es el nombre de la forma geométrica de las curvas de nivel?

c. Dar la ecuación general de las curvas de nivel.

d. ¿Cuál es el valor máximo de$z$?

e. ¿Cuál es el dominio de la función?

f. ¿Cuál es el rango de la función?

Responder

a.

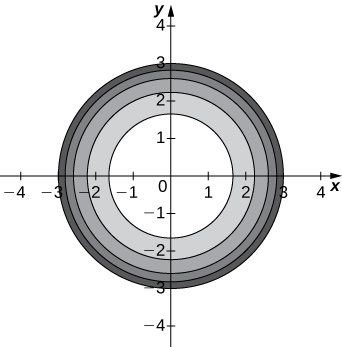
b. Las curvas de nivel son círculos centrados en$(0,0)$ con radio$9−c$.
c.$x^2+y^2=9−c$
d.$z=3$
e.$\{(x,y)∈R^2∣x^2+y^2≤9\}$
f.$\{z|0≤z≤3\}$

48) Verdadero o Falso: Si evaluamos$\displaystyle \lim_{(x,y)→(0,0)}f(x)$ a lo largo de varios caminos y cada vez que el límite es$1$, podemos concluir que$\displaystyle \lim_{(x,y)→(0,0)}f(x)=1.$

49) Usa coordenadas polares para encontrar También$\displaystyle \lim_{(x,y)→(0,0)}\frac{\sin\sqrt{x^2+y^2}}{\sqrt{x^2+y^2}}.$ puedes encontrar el límite usando la regla de L'Hôpital.

Responder

$\displaystyle \lim_{(x,y)→(0,0)}\frac{\sin\sqrt{x^2+y^2}}{\sqrt{x^2+y^2}} = 1$

50) Usa coordenadas polares para encontrar$\displaystyle \lim_{(x,y)→(0,0)}\cos(x^2+y^2).$

51) Discutir la continuidad de$f(g(x,y))$ dónde$f(t)=1/t$ y$g(x,y)=2x−5y.$

Responder

$f(g(x,y))$es continuo en todos los puntos$(x,y)$ que no están en la línea$2x−5y=0.$

52) Dado$f(x,y)=x^2−4y,$ hallazgo$\displaystyle \lim_{h→0}\frac{f(x+h,y)−f(x,y)}{h}.$

53) Dado$f(x,y)=x^2−4y,$ hallazgo$\displaystyle \lim_{h→0}\frac{f(1+h,y)−f(1,y)}{h}$.

Responder

$\displaystyle \lim_{h→0}\frac{f(1+h,y)−f(1,y)}{h} = 2$

Colaboradores

• Template:ContribOpenStaxCalc
• Paul Seeburger (Monroe Community College) created problem 1.