15.1: Integrales dobles sobre regiones rectangulares

Objetivos de aprendizaje

• Reconocer cuando una función de dos variables es integrable sobre una región rectangular.
• Reconocer y utilizar algunas de las propiedades de las dobles integrales.
• Evalúe una doble integral sobre una región rectangular escribiéndola como una integral iterada.
• Utilice una doble integral para calcular el área de una región, el volumen bajo una superficie o el valor promedio de una función sobre una región plana.

En esta sección investigamos las integrales dobles y mostramos cómo podemos utilizarlas para encontrar el volumen de un sólido sobre una región rectangular en el plano xy. Muchas de las propiedades de las integrales dobles son similares a las que ya hemos discutido para integrales simples.

Volúmenes e Integrales Dobles

Comenzamos considerando el espacio sobre una región rectangular$R$. Considere una función continua$f(x,y)≥0$ de dos variables definidas en el rectángulo cerrado$R$:

$$R=[a,b] \times [c,d]= \left\{(x,y) ∈ \mathbb{R}^2| \, a ≤ x ≤ b, \, c ≤ y ≤ d \right\} \nonumber$$

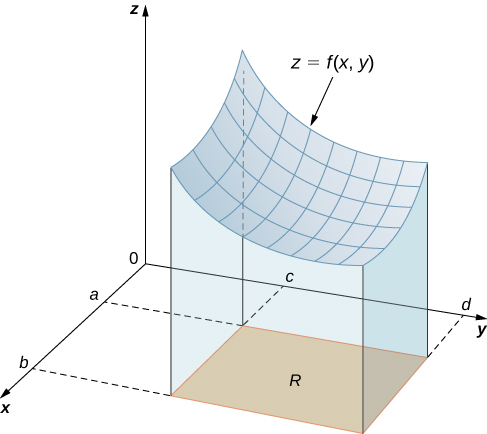
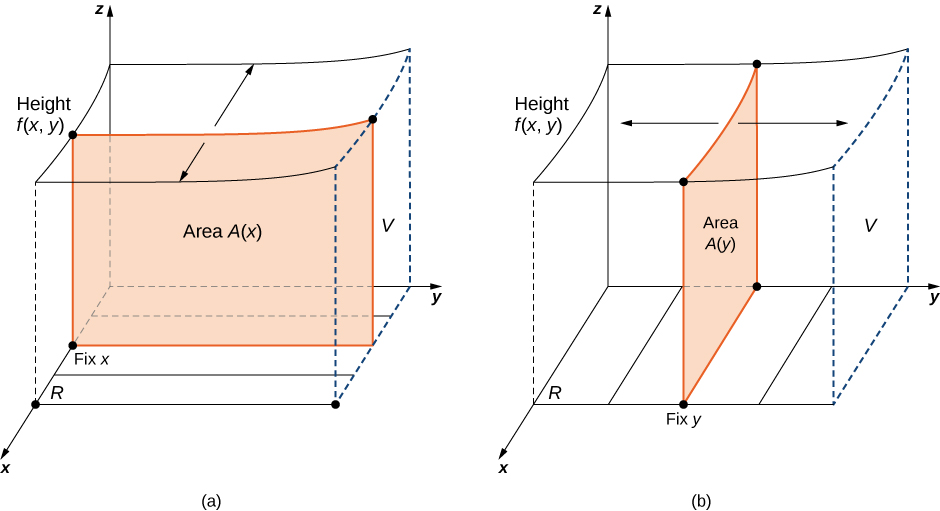
Aquí$[a,b] \times [c,d]$ denota el producto cartesiano de los dos intervalos cerrados$[a,b]$ y$[c,d]$. Consta de pares rectangulares$(x,y)$ tales que$a≤x≤b$ y$c≤y≤d$. La gráfica de$f$ representa una superficie por encima del$xy$ plano -con ecuación$z = f(x,y)$ donde$z$ está la altura de la superficie en el punto$(x,y)$. Dejar$S$ ser el sólido que se encuentra arriba$R$ y debajo de la gráfica de$f$ (Figura$\PageIndex{1}$). La base del sólido es el rectángulo$R$ en el$xy$ plano. Queremos encontrar el volumen$V$ del sólido$S$.

Figura$\PageIndex{1}$: La gráfica de$f(x,y)$ sobre el rectángulo R en el$xy$ plano -es una superficie curva.

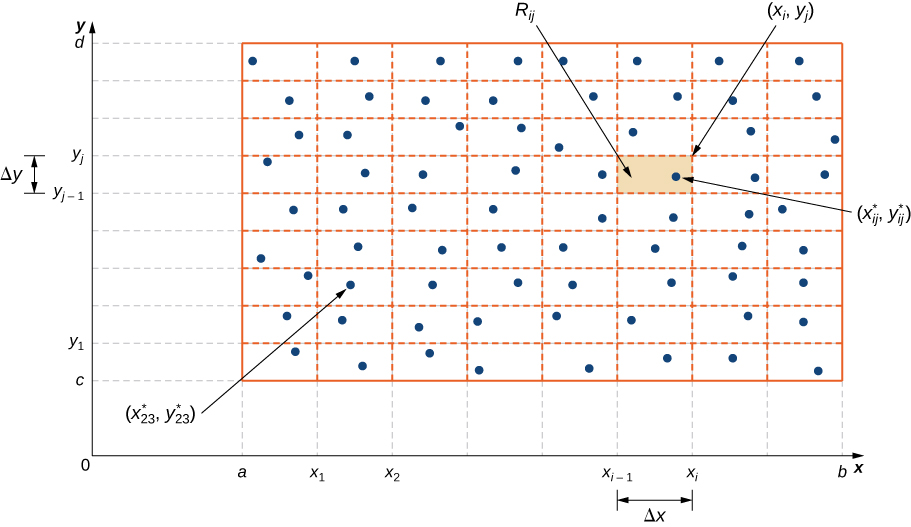
Dividimos la región$R$ en pequeños rectángulos$R_{ij}$, cada uno con área$ΔA$ y con lados$Δx$ y$Δy$ (Figura$\PageIndex{2}$). Esto lo hacemos dividiendo el intervalo$[a,b]$ en$m$ subintervalos y dividiendo el intervalo$[c,d]$ en$n$ subintervalos. De ahí$\Delta x = \frac{b - a}{m}$,$\Delta y = \frac{d - c}{n}$, y$\Delta A = \Delta x \Delta y$.

Figura$\PageIndex{2}$:$R$ El rectángulo se divide en pequeños rectángulos$R_{ij}$ cada uno con área$\Delta A$.

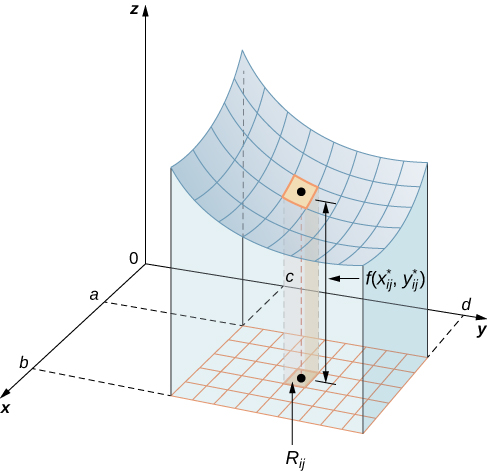
El volumen de una caja rectangular delgada arriba$R_{ij}$ es$f(x_{ij}^*, \, y_{ij}^*)\,\Delta A$, donde ($x_{ij}^*, \, y_{ij}^*$) es un punto de muestra arbitrario en cada uno$R_{ij}$ como se muestra en la siguiente figura,$f(x_{ij}^*, \, y_{ij}^*)$ es la altura de la caja rectangular delgada correspondiente, y$\Delta A$ es el área de cada rectángulo$R_{ij}$.

Figura$\PageIndex{3}$: Una delgada caja rectangular arriba$R_{ij}$ con altura$f(x_{ij}^*, \, y_{ij}^*)$.

Usando la misma idea para todos los subrectángulos, obtenemos un volumen aproximado del sólido S como

$$V \approx \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, \, y_{ij}^*)\Delta A. \nonumber$$

Esta suma se conoce como una suma doble de Riemann y se puede utilizar para aproximar el valor del volumen del sólido. Aquí la suma doble significa que para cada subrectángulo evaluamos la función en el punto elegido, multiplicamos por el área de cada rectángulo, y luego sumamos todos los resultados.

Como hemos visto en el caso de una sola variable, obtenemos una mejor aproximación al volumen real si$m$ y$n$ se hacen más grandes.

$$V = \lim_{m,n \rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, \, y_{ij}^*) \Delta A \nonumber$$

o

$$V=\lim_{\Delta x, \, \Delta y \rightarrow 0} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, \, y_{ij}^*)\Delta A. \nonumber$$

Tenga en cuenta que la suma se acerca a un límite en cualquier caso y el límite es el volumen del sólido con la base$R$. Ahora estamos listos para definir la doble integral.

Definición: Doble Integral sobre una Región Rectangular R

La doble integral de la función$f(x, \, y)$ sobre la región rectangular$R$ en el$xy$ plano se define como

$$\iint_R f(x, \, y) dA = \lim_{m,n \rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, \, y_{ij}^*)\Delta A. \nonumber$$

Si$f(x,y)\geq 0$, then the volume $V$ of the solid $S$, which lies above $R$ in the $xy$-plane and under the graph of $f$, is the double integral of the function $f(x,y)$ over the rectangle $R$. If the function is ever negative, then the double integral can be considered a “signed” volume in a manner similar to the way we defined net signed area in La Integral Definitiva.

Ejemplo$\PageIndex{1}$: Setting up a Double Integral and Approximating It by Double Sums

Considere la función$z = f(x, \, y) = 3x^2 - y$ sobre la región rectangular$R = [0, 2] \times [0, 2]$ (Figura$\PageIndex{4}$).

1. Establecer una doble integral para encontrar el valor del volumen firmado del sólido$S$ que se encuentra por encima$R$ y “debajo” de la gráfica de$f$.
2. $R$Dividir en cuatro cuadrados con$m = n = 2$, y elegir el punto de muestreo como el punto de esquina superior derecha de cada cuadrado (1,1), (2,1), (1,2), y (2,2) (Figura$\PageIndex{4}$) para aproximar el volumen firmado del sólido$S$ que se encuentra por encima$R$ y “debajo” de la gráfica de$f$.
3. $R$Dividir en cuatro cuadrados con$m = n = 2$, y elegir el punto de muestreo como el punto medio de cada cuadrado: (1/2, 1/2), (3/2, 1/2), (1/2,3/2), y (3/2, 3/2) para aproximar el volumen firmado.

   

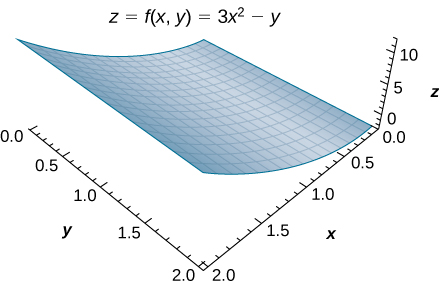
   Figura$\PageIndex{4}$: La función$z=f(x,y)$ graficada sobre la región rectangular$R=[0,2]×[0,2]$.

Solución

1. Como podemos ver, la función$z = f(x,y) = 3x^2 - y$ está por encima del plano. Para encontrar el volumen firmado de$S$, necesitamos dividir la región$R$ en pequeños rectángulos$R_{ij}$, cada uno con área$ΔA$ y con lados y$Δy$,$Δx$ y elegir$(x_{ij}^*, y_{ij}^*)$ como puntos de muestra en cada uno$R_{ij}$. Por lo tanto, una doble integral se configura como

   $$V = \iint_R (3x^2 - y) dA = \lim_{m,n→∞} \sum_{i=1}^m \sum_{j=1}^n [3(x_{ij}^*)^2 - y_{ij}^*] \Delta A. \nonumber$$

2. Aproximando el volumen firmado usando una suma de Riemann con$m = n = 2$ tenemos$\Delta A = \Delta x \Delta y = 1 \times 1 = 1$. Además, los puntos de muestreo son (1, 1), (2, 1), (1, 2) y (2, 2) como se muestra en la siguiente figura.

Figura$\PageIndex{5}$: Subrectángulos para la región rectangular$R=[0,2]×[0,2]$.

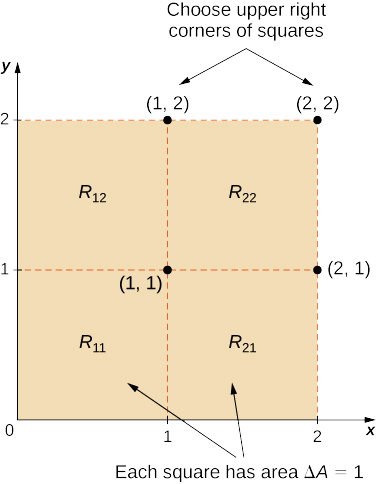
De ahí que,

\ [\ begin {align*} V &\ approx\ suma_ {i=1} ^2\ suma_ {j=1} ^2 f (x_ {ij} ^*, y_ {ij} ^*)\ Delta A\\ [4pt]
&=\ suma_ {i=1} ^2 (f (x_ {i1} ^*, y_ {i1} ^*) + f (x_ {i2} ^*, y_ {i2} ^*))\ Delta A\\ [4pt]
&=f (x_ {11} ^*, y_ {11} ^*)\ Delta A + f (x_ {21} ^*, y_ {21} ^*)\ Delta A + f (x_ {12} ^*, y_ {12} ^*) Delta\ A + f (x_ {22} ^*, y_ {22} ^*)\ Delta A\\ [4pt]
&= f (1,1) (1) + f (2,1) (1) + f (1,2) (1) + f (2,2) (1)\\ [4pt]
&= (3 - 1) (1) + (12 - 1) (1) + (3 - 2) (1) + (12 - 2) (1)\\ [4pt]
&= 2 + 11 + 1 + 10 = 24. \ end {alinear*}\]

3. Aproximando el volumen firmado usando una suma de Riemann con$m = n = 2$ tenemos$\Delta A = \Delta x \Delta y = 1 \times 1 = 1$. En este caso los puntos de muestra son (1/2, 1/2), (3/2, 1/2), (1/2, 3/2), y (3/2, 3/2).
   Por lo tanto,
   \ [\ begin {align*} V &\ approx\ suma_ {i=1} ^2\ suma_ {j=1} ^2 f (x_ {ij} ^*, y_ {ij} ^*)\ Delta A\\ [4pt]
   &=f (x_ {11} ^*, y_ {11} ^*)\ Delta A + f (x_ {21} ^*, y_ {21} ^*)\ Delta A + f (x_ {12} ^*, y_ {12} ^*)\ Delta A + f (x_ {22} ^*, y_ {22} ^*)\ Delta A\\ [4pt]
   &= f (1/2,1/2) (1) + f (3/2,1/2) (1) + f (1/2,3/2) (1) + f (3/2,3/2) (1)\\ [4pt]
   &=\ izquierda (\ frac {3} {4} -\ frac {1} {4}\ derecha) (1) +\ izquierda (\ frac {27} {4} -\ frac {1} {2}\ derecha) (1) +\ izquierda (\ frac {3} {4} -\ frac {3} {2}\ derecha) (1) +\ izquierda (\ frac {27} {4} -\ frac {3} {2}\ derecha) (1)\\ [4pt]
   &=\ frac {2} {4} +\ frac {25} {4} +\ izquierda (-\ frac {3} {4}\ derecha) +\ frac {21} {4} =\ frac {45} {4} = 11. \ end {alinear*}\]

Análisis

Observe que las respuestas aproximadas difieren debido a las elecciones de los puntos de muestra. En cualquier caso, estamos introduciendo algún error porque estamos usando sólo unos pocos puntos de muestreo. Por lo tanto, necesitamos investigar cómo podemos lograr una respuesta precisa.

Ejercicio$\PageIndex{1}$

Utilice la misma función$z = f(x, y) = 3x^2 - y$ sobre la región rectangular$R=[0,2]×[0,2]$.

$R$Dividir en los mismos cuatro cuadrados con$m = n = 2$, y elegir los puntos de muestra como el punto de esquina superior izquierda de cada cuadrado (0,1), (1,1), (0,2), y (1,2) (Figura$\PageIndex{5}$) para aproximar el volumen firmado del sólido$S$ que se encuentra por encima$R$ y “debajo” de la gráfica de$f$.

Pista

Sigue los pasos del ejemplo anterior.

Responder

$$V \approx \sum_{i=1}^2 \sum_{j=1}^2 f(x_{ij}^*, y_{ij}^*)\,\Delta A = 0 \nonumber$$

Tenga en cuenta que desarrollamos el concepto de doble integral utilizando una región rectangular$R$. Este concepto puede extenderse a cualquier región general. Sin embargo, cuando una región no es rectangular, es posible que los subrectángulos no encajen perfectamente$R$, especialmente si el área base es curva. Examinamos esta situación con más detalle en la siguiente sección, donde estudiamos regiones que no siempre son rectangulares y los subrectángulos pueden no encajar perfectamente en la región$R$. Además, las alturas pueden no ser exactas si la superficie$z=f(x,y)$ es curva. Sin embargo, los errores en los lados y la altura donde las piezas pueden no encajar perfectamente dentro del sólido se$S$ acercan a 0 como$m$ y se$n$ acercan al infinito. Además, la doble integral de la función$z=f(x,y)$ existe siempre que la función no$f$ sea demasiado discontinua. Si la función es acotada y continua sobre$R$ excepto en un número finito de curvas suaves, entonces existe la doble integral y decimos que ff es integrable over$R$.

Ya que$\Delta A = \Delta x \Delta y = \Delta y \Delta x$, podemos expresarnos$dA$ como$dx \, dy$ o$dy \, dx$. Esto significa que, cuando estamos usando coordenadas rectangulares, la doble integral sobre una región$R$ denotada por

$$\iint_R f(x,y)\,dA \nonumber$$

se puede escribir como

$$\iint_R f(x,y)\,dx\,dy \nonumber$$

o

$$\iint_R f(x,y)\,dy\,dx. \nonumber$$

Ahora enumeremos algunas de las propiedades que pueden ser útiles para calcular integrales dobles.

Propiedades de Integrales Dobles

Las propiedades de las dobles integrales son muy útiles a la hora de calcularlas o de otra manera trabajar con ellas. Enlistamos aquí seis propiedades de dobles integrales. Las propiedades 1 y 2 son referidas como la linealidad de la integral, la propiedad 3 es la aditividad de la integral, la propiedad 4 es la monotonicidad de la integral, y la propiedad 5 se utiliza para encontrar los límites de la integral. Se utiliza la propiedad 6 si$f(x,y)$ es producto de dos funciones$g(x)$ y$h(y)$.

Teorema: Propiedades de las Integrales Dobles

Supongamos que las funciones$f(x,y)$ y$g(x,y)$ son integrables sobre la región rectangular$R$;$S$ y$T$ son subregiones de$R$; y asumir que$m$ y$M$ son números reales.

1. La suma$f(x,y)+g(x,y)$ es integrable y

$$\iint_R [f(x, y) + g(x, y)]\,dA = \iint_R f(x,y)\, dA + \iint_R g(x, y) \,dA. \nonumber$$

2. Si c es una constante, entonces$cf(x,y)$ es integrable y

$$\iint_R cf(x,y)\,dA = c\iint_R f(x,y)\,dA. \nonumber$$

3. Si$R=S∪T$ y$S∩T=∅$ excepto una superposición en los límites, entonces

$$\iint_R f(x,y)\,dA = \iint_S f(x,y) \,dA + \iint_T f(x,y)\, dA. \nonumber$$

4. Si$f(x,y) \geq g(x,y)$ por$(x,y)$ dentro$R$, entonces

$$\iint_R f(x,y)\,dA \geq \iint_R g(x,y)\,dA. \nonumber$$

5. Si$m \leq f(x,y) \leq M$ y$A(R) = \, \text{the area of}\,R$, entonces

$$m \cdot A(R) \leq \iint_R f(x,y)\,dA \leq M \cdot A(R). \nonumber$$

6. En el caso en que se$f(x,y)$ pueda factorizar como producto de una función$g(x)$ de$x$ solo y una función$h(y)$ de$y$ solo, entonces sobre la región$R = \big\{(x,y) \,|\,a \leq x \leq b, \, c \leq y \leq d \big\}$, la doble integral puede escribirse como

$$\iint_R f(x,y)\,dA = \left(\int_a^b g(x)\,dx \right)\left(\int_c^d h(y) \,dy \right). \nonumber$$

Estas propiedades se utilizan en la evaluación de dobles integrales, como veremos más adelante. Nos volveremos expertos en el uso de estas propiedades una vez que nos familiaricemos con las herramientas computacionales de las dobles integrales. Entonces vamos a llegar a eso ahora.

Integrales iteradas

Hasta el momento, hemos visto cómo configurar una doble integral y cómo obtener un valor aproximado para ello. También podemos imaginar que evaluar las dobles integrales mediante el uso de la definición puede ser un proceso muy largo si elegimos valores mayores para$m$ y$n$ .Por lo tanto, necesitamos una técnica práctica y conveniente para computar dobles integrales. En otras palabras, necesitamos aprender a calcular las dobles integrales sin emplear la definición que usa límites y sumas dobles.

La idea básica es que la evaluación se vuelve más fácil si podemos romper una doble integral en integrales individuales integrando primero con respecto a una variable y luego con respecto a la otra. La herramienta clave que necesitamos se llama integral iterada.

Definiciones: Integrales iteradas

Supongamos$a$$b$,$c$,, y$d$ son números reales. Definimos una integral iterada para una función$f(x,y)$ sobre la región rectangular$R =[a,b]×[c,d]$ como

$$\int_a^b\int_c^d f(x,y)\,dy \, dx = \int_a^b \left[\int_c^d f(x,y)\,dy \right] dx \nonumber$$

o

$$\int_c^d \int_a^b f(x,y)\,dx \, dy = \int_c^d \left[\int_a^b f(x,y)\,dx \right] dy. \nonumber$$

La notación$\int_a^b \left[\int_c^d f(x,y)\,dy \right] dx$ significa que integramos$f(x,y)$ con respecto a$y$ mientras mantenemos$x$ constantes. De igual manera, la notación$\int_c^d \left[\int_a^b f(x,y)\,dx \right] dy$ significa que integramos$f(x,y)$ con respecto a$x$ mientras mantenemos$y$ constantes. El hecho de que las dobles integrales se pueden dividir en integrales iteradas se expresa en el teorema de Fubini. Piense en este teorema como una herramienta esencial para evaluar las dobles integrales.

Teorema: Teorema de Fubini

Supongamos que$f(x,y)$ es una función de dos variables que es continua sobre una región rectangular$R = \big\{(x,y) ∈ \mathbb{R}^2 | \, a \leq x \leq b, \, c \leq y \leq d \big\}$. Entonces vemos en la Figura$\PageIndex{6}$ que la doble integral de$f$ sobre la región es igual a una integral iterada,

$$\iint_R f(x,y)\,dA = \iint_R f(x,y)\,dx \, dy = \int_a^b \int_c^d f(x,y)\,dy \, dx = \int_c^d \int_a^b f(x,y)\,dx \, dy. \nonumber$$

De manera más general, el teorema de Fubini$f$ es cierto si está limitado$R$ y$f$ es discontinuo solo en un número finito de curvas continuas. En otras palabras,$f$ tiene que ser integrable sobre$R$.

Figura$\PageIndex{6}$: (a) Integrando primero con respecto$y$ y luego con respecto$x$ a encontrar el área$A(x)$ y luego el volumen$V$; (b) integrando primero con respecto$x$ y luego con respecto$y$ a encontrar el área$A(y)$ y luego el volumen $V$.

Ejemplo$\PageIndex{2}$: Using Fubini’s Theorem

Utilice el teorema de Fubini para calcular la doble integral$\displaystyle \iint_R f(x,y) \,dA$ dónde$f(x,y) = x$ y$R = [0, 2] \times [0, 1]$.

Solución

El teorema de Fubini ofrece una manera más fácil de evaluar la doble integral mediante el uso de una integral iterada. Observe cómo los valores límite de la región$R$ se convierten en los límites superior e inferior de integración.

\ [\ begin {alinear*}\ iint_r f (x, y)\, dA &=\ iInt_r f (x, y)\, dx\, dy\\ [4pt]
&=\ int_ {y=0} ^ {y=1}\ int_ {x=0} ^ {x=2} x\, dx\, dy\ [4pt]
&=\ int_ {y=0} ^ {y=1}\ izquierda [\ frac {x^2} {2}\ bigg|_ {x=0} ^ {x=2}\ derecha]\, dy\\ [4pt]
&=\ int_ {y=0} ^ {y=1} 2\, dy = 2y\ bigg|_ {y=0 } ^ {y=1} = 2\ final {alinear*}\]

La doble integración en este ejemplo es lo suficientemente simple como para usar directamente el teorema de Fubini, lo que nos permite convertir una doble integral en una integral iterada. En consecuencia, ahora estamos listos para convertir todas las dobles integrales en integrales iteradas y demostrar cómo las propiedades enumeradas anteriormente pueden ayudarnos a evaluar las dobles integrales cuando la función$f(x,y)$ es más compleja. Tenga en cuenta que se puede cambiar el orden de integración (ver Ejemplo 7).

Ejemplo$\PageIndex{3}$: Illustrating Properties i and ii

Evaluar la doble integral $$\iint_R (xy - 3xy^2) \,dA, \, \text{where} \, R = \big\{(x,y) \,| \, 0 \leq x \leq 2, \, 1 \leq y \leq 2 \big\}.\nonumber$$

Solución

Esta función tiene dos piezas: una pieza es$xy$ y la otra es$3xy^2$. Además, la segunda pieza tiene una constante 3. Observe cómo utilizamos las propiedades i y ii para ayudar a evaluar la doble integral.

\ [\ begin {align*}\ iint_r (xy - 3xy^2)\, dA &=\ iInt_r xy\, dA +\ iint_r (-3xy^2)\, dA & &\ text {Propiedad i: Integral de una suma es la suma de las integrales.}\\ [4pt]
&=\ int_ {y=1} ^ {y=2}\ int_ _ {x=0} ^ {x=2} xy\, dx\, dy -\ int_ {y=1} ^ {y=2}\ int_ {x=0} ^ {x=2} 3xy^2\, dx\, dy &\ text {Convertir integrales dobles en integrales iteradas.}\\ [4pt]
&=\ int_ {y=1} ^ {y=2}\ left (\ frac {x^2} {2} y\ right)\ big|_ {x=0} ^ {x=2}\, dy - 3\ int_ {y=1} ^ {y=2}\ left (\ frac {x^^2} {2} y^2\ right)\ bigg|_ {x=0} ^ {x=2}\, dy & &\ text {Integrar con respecto a $x$, manteniendo $y$ constante.}\\ [4pt]
&=\ int_ {y=1} ^ {y=2} 2y\, dy -\ int_ {y=1} ^ {y=2} 6y^2 dy & &\ text {Propiedad ii: Colocando la constante antes de la integral.}\\ [4pt]
&= 2\ int_1^2 y\, dy - 6\ int_1^2 y^2\, dy & &\ text Integrar {con respecto a y.}\\ [4pt]
&= 2\ frac {y^2} {2}\ bigg|_1^2 - 6\ frac {y^3} {3}\ bigg|_1^2\\ [4pt]
&=y^2\ bigg|_1^2 - 2y^3\ bigg|_1^2\\ [4pt]
& =( 4−1) − 2 (8−1) = 3 − 2 (7) = 3 − 14 = −11. \ end {alinear*}\]

Ejemplo$\PageIndex{4}$: Illustrating Property v.

Sobre la región$R = \big\{(x,y)\,| \, 1 \leq x \leq 3, \, 1 \leq y \leq 2 \big\}$, tenemos$2 \leq x^2 + y^2 \leq 13$. Encuentra un límite inferior y uno superior para la integral$\displaystyle \iint_R (x^2 + y^2)\,dA.$

Solución

Para un límite inferior, integre la función constante 2 sobre la región$R$. Para un límite superior, integre la función constante 13 sobre la región$R$.

$$\begin{align*} \int_1^2 \int_1^3 2 \,dx \, dy &= \int_1^2 [2x\bigg|_1^3] \,dy = \int_1^2 2(2)dy = 4y\bigg|_1^2 = 4(2 - 1) = 4 \\[4pt] \int_1^2 \int_1^3 13dx \, dy &= \int_1^2 [13x\bigg|_1^3] \,dy = \int_1^2 13(2)\,dy = 26y\bigg|_1^2 = 26(2 - 1) = 26. \end{align*}$$

De ahí que obtengamos$\displaystyle 4 \leq \iint_R (x^2 + y^2) \,dA \leq 26.$

Ejemplo$\PageIndex{5}$: Illustrating Property vi

Evaluar la integral$\displaystyle \iint_R e^y \cos x \, dA$ en la región$R = \big\{(x,y)\,| \, 0 \leq x \leq \frac{\pi}{2}, \, 0 \leq y \leq 1 \big\}$.

Solución

Este es un gran ejemplo para la propiedad vi porque la función$f(x,y)$ es claramente el producto de dos funciones de una sola variable$e^y$ y$\cos x$. Así podemos dividir la integral en dos partes y luego integrar cada una como un problema de integración de una sola variable.

\ [\ begin {align*}\ iint_r e^y\ cos x\, dA &=\ int_0^1\ int_0^ {\ pi/2} e^y\ cos x\, dx\, dy\ [4pt]
&=\ izquierda (\ int_0^1 e^y dy\ derecha)\ izquierda (\ int_0^ {\ pi/2}\ cos x\, dx\ derecha)\\ [4pt]
&= (e^y\ bigg|_0^1) (\ sin x\ bigg|_0^ {\ pi/2})\\ [4pt]
&= e - 1. \ end {alinear*}\]

Ejercicio$\PageIndex{2}$

a. Utilizar las propiedades de la doble integral y del teorema de Fubini para evaluar la integral

$$\int_0^1 \int_{-1}^3 (3 - x + 4y) \,dy \, dx. \nonumber$$

b. Demostrar que$\displaystyle 0 \leq \iint_R \sin \pi x \, \cos \pi y \, dA \leq \frac{1}{32}$ dónde$R = \left(0, \frac{1}{4}\right)\left(\frac{1}{4}, \frac{1}{2}\right)$.

Pista

Utilice las propiedades i. y ii. y evalúe la integral iterada, y luego use la propiedad v.

Responder

a.$26$

b. Las respuestas pueden variar.

Como mencionamos anteriormente, cuando estamos usando coordenadas rectangulares, la doble integral sobre una región$R$ denotada por se$\iint_R f(x,y) \, dA$ puede escribir como$\iint_R\, f(x,y) \, dx \, dy$ o$\iint_R \, f(x,y) \,dy \, dx.$ El siguiente ejemplo muestra que los resultados son los mismos independientemente del orden de integración que elijamos.

Ejemplo$\PageIndex{6}$: Evaluating an Iterated Integral in Two Ways

Volvamos a la función$f(x,y) = 3x^2 - y$ del Ejemplo 1, esta vez sobre la región rectangular$R = [0,2] \times [0,3]$. Usa el teorema de Fubini para evaluar$\iint_R f(x,y) \,dA$ de dos maneras diferentes:

1. Primero integrar con respecto$y$ y luego con respecto a$x$;
2. Primero integrar con respecto$x$ y luego con respecto a$y$.

Solución

La figura$\PageIndex{6}$ muestra cómo funciona el cálculo de dos maneras diferentes.

1. Primero integrar con respecto a$y$ y luego integrar con respecto a$x$:

\ [\ begin {alinear*}\ iint_r f (x, y)\, dA &=\ int_ {x=0} ^ {x=0} ^ {x=0} ^ {y=3} (3x^2 - y)\, dy\, dx\ [4pt]
&=\ int_ {x=0} ^ {x=2}\ izquierda (\ int_ {y=0} ^ {y=3} (3x^2 - y)\, dy\ derecha)\, dx =\ int_ {x=0} ^ {x=2}\ izquierda [3x^2y -\ frac {y^2} {2}\ big|_ {y=0} ^ {y=3}\ derecha]\, dx\\ [4pt]
&=\ int_ {=0} ^ {x=2}\ izquierda (9x^2 -\ frac {9} {2}\ derecha)\, dx = 3x^3 -\ frac {9} {2} x\ bigg|_ {x=0} ^ {x=2} = 15. \ end {alinear*}\]

2. Primero integre con respecto a$x$ y luego integre con respecto a$y$:
   \ [\ begin {align*}\ iInt_r f (x, y)\, dA &=\ int_ {y=0} ^ {y=3}\ int_ {x=0} ^ {x=2} (3x^2 - y)\, dx\, dy\ [4pt]
   &=\ int_ {y=0} {y=3}\ izquierda (\ int_ {x=0} ^ {x=2} (3x^2 - y)\, dx\ derecha)\, dy \\ [4pt]
   &=\ int_ {y=0} ^ {y=3}\ izquierda [x^3 - xy\ bigg|_ {x=0} ^ {x=2}\ derecha] dy\\ [4pt]
   &=\ int_ {y=0} ^ {y=3} (8 - 2y)\, dy = 8y - y^2\ bigg|_ {y=0} ^ {y=3} = 15. \ end {alinear*}\]

Análisis

Con cualquier orden de integración, la doble integral nos da una respuesta de$15$. Podríamos querer interpretar esta respuesta como un volumen en unidades cúbicas del sólido$S$ debajo de la función$f(x,y) = 3x^2 - y$ sobre la región$R = [0,2] \times [0,3]$. Sin embargo, recuerde que la interpretación de una doble integral como volumen (sin signo) funciona solo cuando el integrando$f$ es una función no negativa sobre la región base$R$.

Ejercicio$\PageIndex{3}$

Evaluar

$$\int_{y=-3}^{y=2} \int_{x=3}^{x=5} (2 - 3x^2 + y^2) \,dx \, dy. \nonumber$$

Pista

Usa el teorema de Fubini.

Responder

$-\frac{1340}{3}$

En el siguiente ejemplo vemos que en realidad puede ser beneficioso cambiar el orden de integración para facilitar el cálculo. Volveremos a esta idea varias veces en este capítulo.

Ejemplo$\PageIndex{7}$: Switching the Order of Integration

Considera la doble integral$\displaystyle \iint_R x \, \sin (xy) \, dA$ sobre la región$R = \big\{(x,y) \,| \, 0 \leq x \leq \pi, \, 1 \leq y \leq 2 \big\}$ (Figura$\PageIndex{7}$).

1. Exprese la doble integral de dos maneras diferentes.
2. Analizar si evaluar la doble integral de una manera es más fácil que la otra y por qué.
3. Evaluar la integral.

Figura$\PageIndex{7}$: La función$z = f(x,y) = x \, \sin(xy)$ sobre la región rectangular$R = [0,\pi ] \times [1,2].$

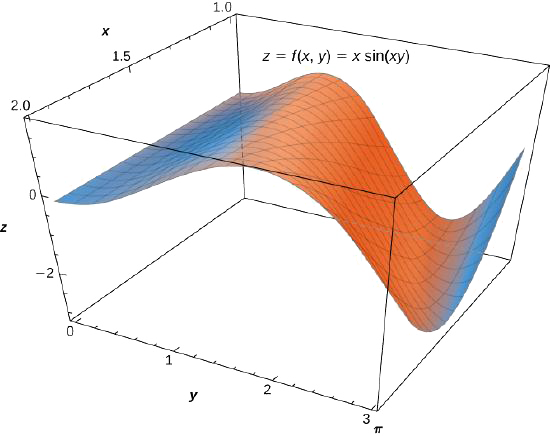
1. Podemos expresarnos$\iint_R x \, \sin (xy) \,dA$ de las dos maneras siguientes: primero integrando con respecto$y$ y luego con respecto a$x$; segundo integrando con respecto a$x$ y luego con respecto a$y$.
   $$\iint_R x \, \sin (xy) \,dA= \int_{x=0}^{x=\pi} \int_{y=1}^{y=2} x \, \sin (xy) \,dy \, dx \nonumber$$
   Integrar primero con respecto a$y$.
   $$= \int_{y=1}^{y=2} \int_{x=0}^{x=\pi} x \, \sin (xy) \,dx \, dy \nonumber$$
   Integrar primero con respecto a$x$.
2. Si queremos integrarnos con respecto a y primero y luego integrarnos con respecto a$x$, vemos que podemos usar la sustitución$u = xy$, que da$du = x \, dy$. De ahí que la integral interna sea simple$\int \sin u \, du$ y podamos cambiar los límites para ser funciones de$x$,

$$\iint_R x \, \sin (xy) \,dA = \int_{x=0}^{x=\pi} \int_{y=1}^{y=2} x \, \sin (xy) \, dy \, dx = \int_{x=0}^{x=\pi} \left[\int_{u=x}^{u=2x} \sin (u) \,du \right] \, dx.\nonumber$$

Sin embargo, la integración con respecto a$x$ primero y luego la integración con respecto a$y$ requiere integración por partes para la integral interna, con$u = x$ y$dv = \sin(xy)dx$

Entonces$du = dx$ y$v = - \frac{\cos(xy)}{y}$, entonces

$$\iint_R x \sin(xy) \,dA = \int_{y=1}^{y=2} \int_{x=0}^{x=\pi} x \sin(xy) \,dx \, dy = \int_{y=1}^{y=2} \left[ - \frac{x \, \cos (xy)}{y} \bigg|_{x=0}^{x=\pi} + \frac{1}{y} \int_{x=0}^{x=\pi} \cos(xy)\,dx \right] \, dy.\nonumber$$

Dado que la evaluación se está complicando, solo haremos el cálculo que sea más fácil de hacer, que es claramente el primer método.

3. Evaluar la doble integral de la manera más fácil.

\ [\ begin {alinear*}\ iint_r x\,\ sin (xy)\, dA &=\ int_ {x=0} ^ {x=\ pi}\ int_ {y=1} ^ {y=2} x\,\ sin (xy)\, dy\, dx\ [4pt]
&=\ int_ {x=0} ^ {x=\ pi}\ izquierda [\ int_ {u=x} ^ {u=2x}\ sin (u)\, du\ derecha]\, dx =\ int_ {x=0} ^ {x=\ pi}\ izquierda [-\ cos u\ big|_ {u=x} ^ {u=2x}\ derecha]\, dx\\ [4pt]
&=\ int _ {x=0} ^ {x=\ pi} (-\ cos 2x +\ cos x)\, dx\\ [4pt]
&=\ izquierda (-\ frac {1} {2}\ sin 2x +\ sin x\ derecha)\ bigg|_ {x=0} ^ {x=\ pi} = 0. \ end {alinear*}\]

Ejercicio$\PageIndex{4}$

Evaluar la integral$\displaystyle \iint_R xe^{xy}\,dA$ donde$R = [0,1] \times [0, \ln 5]$.

Pista

Integrar con respecto a$y$ primero.

Responder

$\frac{4 - \ln 5}{\ln 5}$

Aplicaciones de Integrales Dobles

Las dobles integrales son muy útiles para encontrar el área de una región delimitada por curvas de funciones. Describimos esta situación con más detalle en la siguiente sección. Sin embargo, si la región es de forma rectangular, podemos encontrar su área integrando la función constante$f(x,y) = 1$ sobre la región$R$.

Definición: Área de una Región R

El área de la región$R$ está dada por $$A(R) = \iint_R 1 \, dA. \nonumber$$

Esta definición tiene sentido porque usar$f(x,y) = 1$ y evaluar la integral la convierten en un producto de largo y ancho. Revisemos esta fórmula con un ejemplo y veamos cómo funciona esta.

Ejemplo$\PageIndex{8}$: Finding Area Using a Double Integral

Encontrar el área de la región$R = \big\{\,(x,y)\,|\,0 \leq x \leq 3, \, 0 \leq y \leq 2\big\}$ mediante el uso de una doble integral, es decir, integrando$1$ sobre la región$R$.

Solución

La región es rectangular con largo$3$ y ancho$2$, por lo que sabemos que el área es$6$. Obtenemos la misma respuesta cuando usamos una doble integral:

$$A(R) = \int_0^2 \int_0^3 1 \, dx \, dy = \int_0^2 \left[x\big|_0^3\right] \, dy = \int_0^2 3 dy = 3 \int_0^2 dy = 3y\bigg|_0^2 = 3(2) = 6 \, \text{units}^2.\nonumber$$

Ya hemos visto cómo se pueden utilizar las integrales dobles para encontrar el volumen de un sólido delimitado arriba por una función$f(x,y) \geq 0$ sobre una región$R$ proporcionada$f(x,y) \geq 0$ para all$(x,y)$ in$R$. Aquí hay otro ejemplo para ilustrar este concepto.

Ejemplo$\PageIndex{9}$: Volume of an Elliptic Paraboloid

Encuentra el volumen$V$ del sólido$S$ que está delimitado por el paraboloide elíptico$2x^2 + y^2 + z = 27$, los planos$x = 3$ y$y = 3$, y los tres planos de coordenadas.

Solución

Primero observe la gráfica de la superficie$z = 27 - 2x^2 - y^2$ en la Figura$\PageIndex{8}$ (a) y por encima de la región cuadrada$R_1 = [-3,3] \times [-3,3]$. Sin embargo, necesitamos el volumen del sólido delimitado por el paraboloide elíptico$2x^2 + y^2 + z = 27$, los planos$x = 3$ y$y = 3$, y los tres planos de coordenadas.

Figura$\PageIndex{8}$: (a) La superficie$z = 27 - 2x^2 - y^2$ sobre la región cuadrada$R1 = [−3,3] \times [−3,3]$. b) El sólido$S$ se encuentra bajo la superficie$z = 27 - 2x^2 - y^2$ sobre la región cuadrada$R1 = [0,3] \times [0,3]$.

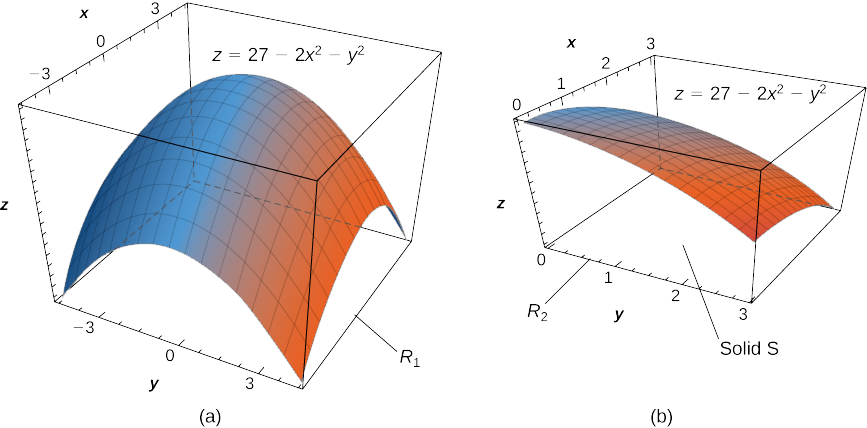
Ahora veamos la gráfica de la superficie en la Figura$\PageIndex{8}$ (b). Determinamos el volumen$V$ evaluando la doble integral sobre$R_2$:

\ [\ begin {align*} V &=\ iint_r z\, dA =\ iint_r (27 - 2x^2 - y^2)\, dA\\ [4pt]
&=\ int_ {y=0} ^ {y=3}\ int_ {x=0} ^ {x=3} (27 - 2x^2 - y^2)\, dx\, & dy &\ text {Convertir a integral literal.}\\ [4pt]
&=\ int_ {y=0} ^ {y=3} [27x -\ frac {2} {3} x^3 - y^2x]\ big|_ {x=0} ^ {x=3}\ , dy & &\ text {Integrar con respecto a $x$.}\\ [4pt]
&=\ int_ {y=0} ^ {y=3} (63 - 3y^2) dy = 63 y - y^3\ bigg|_ {y=0} ^ {y=3} = 162. \ end {alinear*}\]

Ejercicio$\PageIndex{5}$

Encuentra el volumen del sólido delimitado arriba por la gráfica de$f(x,y) = xy \sin(x^2y)$ y abajo por el$xy$ plano -en la región rectangular$R = [0,1] \times [0,\pi]$.

Pista

Grafica la función, configura la integral y usa una integral iterada.

Responder

$\frac{\pi}{2}$

Recordemos que definimos el valor promedio de una función de una variable en un intervalo$[a,b]$ como

$$f_{ave} = \frac{1}{b - a} \int_a^b f(x) \, dx. \nonumber$$

De igual manera, podemos definir el valor promedio de una función de dos variables sobre una región $R$. La principal diferencia es que dividimos por un área en lugar del ancho de un intervalo.

Definición: Valor promedio de una función

El valor promedio de una función de dos variables sobre una región$R$ es

$$F_{ave} = \frac{1}{\text{Area of} \, R} \iint_R f(x,y)\, dx \, dy. \nonumber$$

En el siguiente ejemplo encontramos el valor promedio de una función sobre una región rectangular. Este es un buen ejemplo de obtener información útil para una integración haciendo mediciones individuales sobre una cuadrícula, en lugar de tratar de encontrar una expresión algebraica para una función.

Ejemplo$\PageIndex{10}$: Calculating Average Storm Rainfall

El mapa meteorológico en la Figura$\PageIndex{9}$ muestra un sistema de tormentas inusualmente húmedo asociado con los restos del huracán Karl, que arrojó 4-8 pulgadas (100—200 mm) de lluvia en algunas partes del Medio Oeste del 22 al 23 de septiembre de 2010. El área de lluvia medía 300 millas de este a oeste y 250 millas de norte a sur. Estimar la precipitación promedio en toda el área en esos dos días.

Figura$\PageIndex{9}$: Efectos del huracán Karl, que arrojó 4-8 pulgadas (100—200 mm) de lluvia en algunas partes del suroeste de Wisconsin, el sur de Minnesota y el sureste de Dakota del Sur en un lapso de 300 millas de este a oeste y 250 millas de norte a sur.

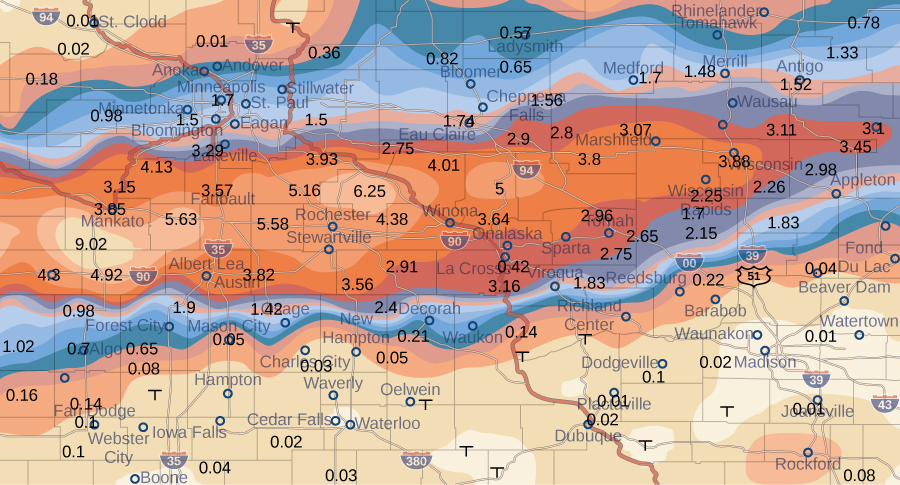
Solución

Colocar el origen en la esquina suroeste del mapa para que todos los valores puedan considerarse como que están en el primer cuadrante y de ahí que todos sean positivos. Ahora divide todo el mapa en seis rectángulos$(m = 2$ y$n = 3)$, como se muestra en la Figura$\PageIndex{9}$. Asumir$f(x,y)$ denota la lluvia pluvial en pulgadas en un punto aproximadamente$x$ millas al este del origen y$y$ millas al norte del origen. Vamos a$R$ representar toda el área de millas$250 \times 300 = 75000$ cuadradas. Entonces el área de cada subrectángulo es

$$\Delta A = \frac{1}{6} (75000) = 12500.\nonumber$$

Supongamos que$(x_{ij}*,y_{ij}*)$ son aproximadamente los puntos medios de cada subrectángulo$R_{ij}$. Anote la región codificada por colores en cada uno de estos puntos y estime la precipitación. La precipitación en cada uno de estos puntos se puede estimar como:

• At ($x_{11}, y_{11}$), la precipitación es de 0.08.
• At ($x_{12}, y_{12}$), la precipitación es de 0.08.
• En ($x_{13}, y_{13}$), la precipitación es de 0.01.
• En ($x_{21}, y_{21}$), la precipitación es de 1.70.
• En ($x_{22}, y_{22}$), la precipitación es de 1.74.
• En ($x_{23}, y_{23}$), la precipitación es de 3.00.

Figura$\PageIndex{10}$: Lluvias pluviales con ejes rectangulares y mostrando los puntos medios de cada subrectángulo.

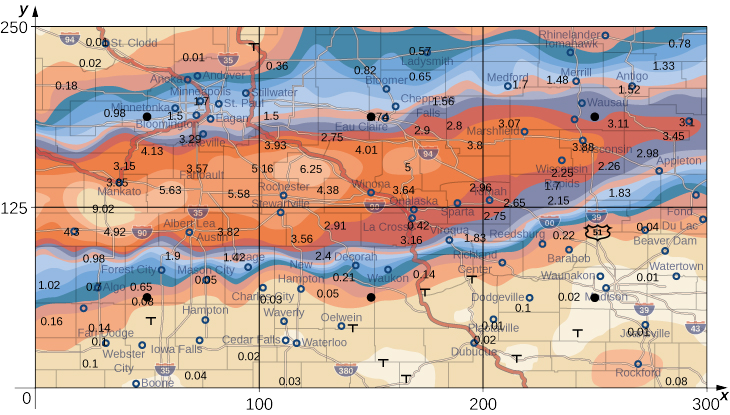
Según nuestra definición, el promedio de lluvias pluviales en toda el área durante esos dos días fue

\ [\ begin {alinear*} f_ {ave} =\ frac {1} {Área\, R}\ iint_r f (x, y)\, dx\, dy &=\ frac {1} {75000}\ iint_r f (x, y)\, dx\, dy\ [4pt]
&\ approx\ frac {1} {75000}\ sum_ {i=1} ^3\ sum_ {j=1} ^2 f (x_ {ij} ^*, y_ {ij} ^*)\ Delta A\\ [4pt]
&=\ frac {1} {75000}\ Bigg [f (x_ {11} ^*, y_ {11} ^*)\ Delta A + f (x_ {12} ^*, y_ {12} ^*)\ Delta A + f (x_ {13} ^*, y_ {13} ^*)\ Delta A + f (x_ {21} ^*, y_ {21} ^*)\ Delta A + f (x_ {22} ^*, y_ {22} ^*)\ Delta A + f (x_ {23} ^*, y_ {23} ^*)\ Delta A\ Bigg]\\ [4pt]
&\ approx\ frac {1} {75000}\ Grande [0.08 + 0.08 + 0.01 + 1.70 + 1.74 + 3.00\ Grande]\ Delta A\\ [4pt]
&=\ frac {1} {75000}\ Grande [0.08 + 0.08 + 0.01 + 1.70 + 1.74 + 3.00\ Grande] 12500\\ [4pt]
&=\ frac {1} {6}\ Grande [0.08 + 0.08 + 0.01 + 1.70 + 1.74 + 3.00\ Grande]\ $$4pt] &\approx 1.10 \;\text{in}. \end{align*}$$

Durante el 22 al 23 de septiembre de 2010 esta zona tuvo una precipitación pluvial promedio de aproximadamente 1.10 pulgadas.

Ejercicio$\PageIndex{6}$

Se muestra un mapa de contorno para una función$f(x,y)$ en el rectángulo$R = [-3,6] \times [-1, 4]$.

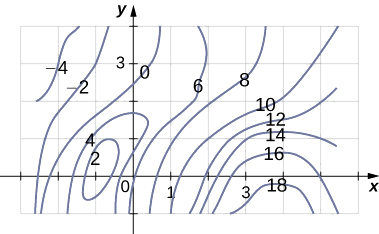
a. Utilice la regla de punto medio con$m = 3$ y$n = 2$ para estimar el valor de$\displaystyle \iint_R f(x,y) \,dA.$

b. Estimar el valor promedio de la función$f(x,y)$.

Pista

Divida la región en seis rectángulos y utilice las curvas de nivel para estimar los valores para$f(x,y)$.

Responder

Las respuestas a ambas partes a. y b. pueden variar.

Conceptos clave

• Podemos usar una suma doble de Riemann para aproximar el volumen de un sólido delimitado arriba por una función de dos variables sobre una región rectangular. Al tomar el límite, ésta se convierte en una doble integral que representa el volumen del sólido.
• Las propiedades de la doble integral son útiles para simplificar el cálculo y encontrar límites en sus valores.
• Podemos usar el teorema de Fubini para escribir y evaluar una doble integral como una integral iterada.
• Las integrales dobles se utilizan para calcular el área de una región, el volumen bajo una superficie y el valor promedio de una función de dos variables sobre una región rectangular.

Ecuaciones Clave

• $$\iint_R f(x,y) \,dA = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(x_ij*,y_ij*)\,ΔA\nonumber$$
• $$\int_a^b \int_c^d f(x,y)\,dx \, dy = \int_a^b \left[\int_c^d f(x,y) \,dy \right] dx\nonumber$$ o

  $$\int_c^d \int_a^b f(x,y)\,dx \, dy = \int_c^d\left[ \int_a^b f(x,y) \,dx \right] dy\nonumber$$

• $$f_{ave} = \frac{1}{\text{Area of}\, R} \iint_R f(x,y) \,dx \, dy\nonumber$$

Glosario

doble integral

de la función$f(x,y)$ sobre la región$R$ en el$xy$ plano -se define como el límite de una suma doble de Riemann,

$$\iint_R f(x,y) \,dA = \lim_{m,n\rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, y_{ij}^*) \,\Delta A.\nonumber$$

doble suma de Riemann

de la función$f(x,y)$ sobre una región rectangular$R$ es

$$\sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, y_{ij}^*) \,\Delta A,\nonumber$$

donde$R$ se divide en subrectángulos más pequeños$R_{ij}$ y$(x_{ij}^*, y_{ij}^*)$ es un punto arbitrario en$R_{ij}$

Teorema de Fubini

si$f(x,y)$ es una función de dos variables que es continua sobre una región rectangular$R = \big\{(x,y) \in \mathbb{R}^2 \,|\,a \leq x \leq b, \, c \leq y \leq d\big\}$, entonces la doble integral de$f$ sobre la región es igual a una integral iterada,

$$\displaystyle\iint_R f(x,y) \, dA = \int_a^b \int_c^d f(x,y) \,dx \, dy = \int_c^d \int_a^b f(x,y) \,dx \, dy\nonumber$$

integral iterada

para una función$f(x,y)$ sobre la región$R$ es

a.$\displaystyle \int_a^b \int_c^d f(x,y) \,dx \, dy = \int_a^b \left[\int_c^d f(x,y) \, dy\right] \, dx,$

b.$\displaystyle \int_c^d \int_a^b f(x,y) \, dx \, dy = \int_c^d \left[\int_a^b f(x,y) \, dx\right] \, dy,$

donde$a,b,c$, y$d$ son los números reales y$R = [a,b] \times [c,d]$