15.2: Integrales dobles sobre regiones generales

Objetivos de aprendizaje

• Reconocer cuando una función de dos variables es integrable en una región general.
• Evaluar una doble integral calculando una integral iterada sobre una región delimitada por dos líneas verticales y dos funciones de\(x\), o dos líneas horizontales y dos funciones de\(y\).
• Simplifique el cálculo de una integral iterada cambiando el orden de integración.
• Utilice integrales dobles para calcular el volumen de una región entre dos superficies o el área de una región plana.
• Resolver problemas que involucran dobles integrales inadecuados.

Anteriormente, estudiamos el concepto de dobles integrales y examinamos las herramientas necesarias para calcularlas. Aprendimos técnicas y propiedades para integrar funciones de dos variables sobre regiones rectangulares. También discutimos varias aplicaciones, como encontrar el volumen delimitado anteriormente por una función sobre una región rectangular, encontrar área por integración y calcular el valor promedio de una función de dos variables.

En esta sección consideramos dobles integrales de funciones definidas sobre una región delimitada general\(D\) en el plano. La mayoría de los resultados anteriores también se mantienen en esta situación, pero algunas técnicas necesitan ser extendidas para cubrir este caso más general.

Regiones Generales de Integración

Un ejemplo de una región delimitada general\(D\) en un plano se muestra en la Figura\(\PageIndex{1}\). Dado que\(D\) está delimitada en el plano, debe existir una región rectangular\(R\) en el mismo plano que encierra la región es\(D\) decir,\(R\) existe una región rectangular tal que\(D\) es un subconjunto de\(R (D \subseteq R)\).

Figura\(\PageIndex{1}\): Para una región\(D\) que es un subconjunto de\(R\), podemos definir una función\(g(x,y)\) para igualar\(f(x,y)\) en cada punto en\(D\) y\(0\) en cada punto de\(R\) no en\(D\).

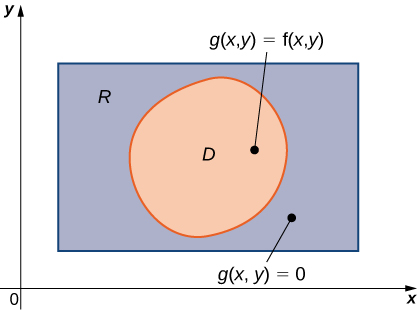
Supongamos que\(z = f(x,y)\) se define en una región delimitada plana general\(D\) como en la Figura\(\PageIndex{1}\). Para desarrollar integrales dobles de\(f\) over\(D\) ampliamos la definición de la función para incluir todos los puntos en la región rectangular\(R\) y luego usar los conceptos y herramientas de la sección anterior. Pero, ¿cómo ampliamos la definición de\(f\) para incluir todos los puntos sobre\(R\)? Esto lo hacemos definiendo una nueva función de\(g(x,y)\) la\(R\) siguiente manera:

\[g(x,y) = \begin{cases} f(x,y), & \text{if} \; (x,y) \; \text{is in}\; D \\[4pt] 0, & \text{if} \;(x,y) \; \text{is in} \; R \;\text{but not in}\; D \end{cases} \nonumber \]

Tenga en cuenta que podríamos tener algunas dificultades técnicas si el límite de\(D\) es complicado. Entonces asumimos que el límite es una curva cerrada simple, lisa y continua por partes. Además, dado que todos los resultados desarrollados en la sección de Integrales dobles sobre regiones rectangulares utilizaron una función integrable\(f(x,y)\) debemos tener cuidado\(g(x,y)\) y verificar que\(g(x,y)\) es una función integrable sobre la región rectangular\(R\). Esto sucede siempre y cuando la región\(D\) esté delimitada por simples curvas cerradas. Por ahora nos concentraremos en las descripciones de las regiones más que en la función y extenderemos nuestra teoría apropiadamente para la integración.

Consideramos dos tipos de regiones delimitadas planas.

Definición: Regiones Tipo I y Tipo II

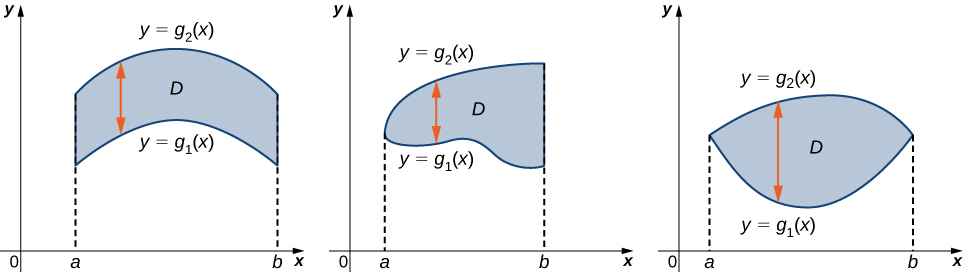
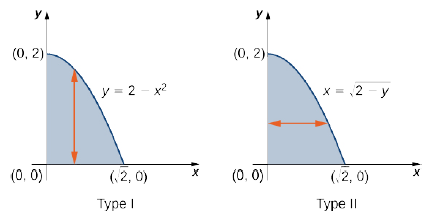
Una región\(D\) en el\((x,y)\) plano -es de Tipo I si se encuentra entre dos líneas verticales y las gráficas de dos funciones continuas\(g_1(x)\) y\(g_2(x)\). Es decir (Figura\(\PageIndex{2}\)),

\[D = \big\{(x,y)\,|\, a \leq x \leq b, \space g_1(x) \leq y \leq g_2(x) \big\}. \nonumber \]

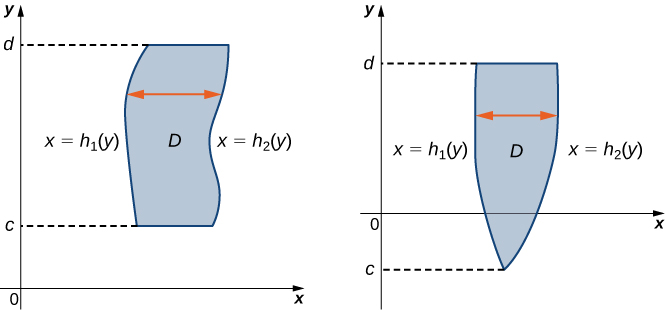
Una región\(D\) en el\(xy\) plano -es de Tipo II si se encuentra entre dos líneas horizontales y las gráficas de dos funciones continuas\(h_1(y)\) y\(h_2(y)\). Es decir (Figura\(\PageIndex{3}\)),

\[D = \big\{(x,y)\,| \, c \leq y \leq d, \space h_1(y) \leq x \leq h_2(y) \big\}. \nonumber \]

Figura\(\PageIndex{2}\). Una región Tipo I se encuentra entre dos líneas verticales y las gráficas de dos funciones de\(x\).

Figura\(\PageIndex{3}\): Una región Tipo II se encuentra entre dos líneas horizontales y las gráficas de dos funciones de\(y\).

Ejemplo\(\PageIndex{1}\): Describing a Region as Type I and Also as Type II

Considerar la región en el primer cuadrante entre las funciones\(y = \sqrt{x}\) y\(y = x^3\) (Figura\(\PageIndex{4}\)). Describir la región primero como Tipo I y luego como Tipo II.

Figura\(\PageIndex{4}\): La región\(D\) puede describirse como Tipo I o como Tipo II.

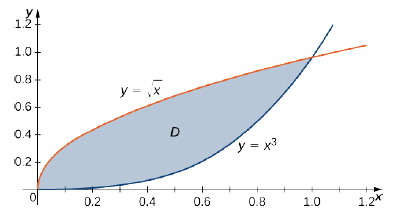
Al describir una región como Tipo I, necesitamos identificar la función que se encuentra por encima de la región y la función que se encuentra debajo de la región. Aquí, la región\(D\) está delimitada arriba\(y = \sqrt{x}\) y abajo por\(y = x^3\) en el intervalo para\(x\) in\([0,1]\). De ahí que, como Tipo I,\(D\) se describa como el conjunto\(\big\{(x,y)\,| \, 0 \leq x \leq 1, \space x^3 \leq y \leq \sqrt[3]{x}\big\}\).

Sin embargo, al describir una región como Tipo II, necesitamos identificar la función que se encuentra a la izquierda de la región y la función que se encuentra a la derecha de la región. Aquí, la región\(D\) está delimitada a la izquierda por\(x = y^2\) y a la derecha por\(x = \sqrt[3]{y}\) en el intervalo para\(y\) in\([0,1]\). De ahí que, como Tipo II,\(D\) se describa como el conjunto\(\big\{(x,y) \,| \, 0 \leq y \leq 1, \space y^2 \leq x \leq \sqrt[3]{y}\big\}\).

Ejercicio\(\PageIndex{1}\)

Considerar la región en el primer cuadrante entre las funciones\(y = 2x\) y\(y = x^2\). Describir la región primero como Tipo I y luego como Tipo II.

Pista

Grafica las funciones y dibuja líneas verticales y horizontales.

Contestar

El tipo I y el tipo II se expresan como\(\big\{(x,y) \,|\, 0 \leq x \leq 2, \space x^2 \leq y \leq 2x\big\}\) y\(\big\{(x,y)|\, 0 \leq y \leq 4, \space \frac{1}{2} y \leq x \leq \sqrt{y}\big\}\), respectivamente.

Integrales dobles sobre regiones no rectangulares

Para desarrollar el concepto y las herramientas de evaluación de una doble integral sobre una región general, no rectangular, necesitamos primero entender la región y poder expresarla como Tipo I o Tipo II o una combinación de ambos. Sin entender las regiones, no podremos decidir los límites de las integraciones en dobles integrales. Como primer paso, veamos el siguiente teorema.

Teorema: Integrales dobles sobre regiones no rectangulares

Supongamos que\(g(x,y)\) es la extensión al rectángulo\(R\) de la función\(f(x,y)\) definida en las regiones\(D\) y\(R\) como se muestra en la Figura\(\PageIndex{1}\) interior\(R\). Entonces\(g(x,y)\) es integrable y definimos la doble integral de\(f(x,y)\) over\(D\) by

\[\iint\limits_D f(x,y) \,dA = \iint\limits_R g(x,y) \,dA. \nonumber \]

El lado derecho de esta ecuación es lo que hemos visto antes, por lo que este teorema es razonable porque\(R\) es un rectángulo y\(\iint\limits_R g(x,y)dA\) ha sido discutido en la sección anterior. También, la igualdad funciona porque los valores de\(g(x,y)\) son\(0\) para cualquier punto\((x,y)\) que quede afuera\(D\) y de ahí estos puntos no agregan nada a la integral. Sin embargo, es importante que el rectángulo\(R\) contenga la región\(D\).

De hecho, si la región\(D\) está delimitada por curvas suaves en un plano y somos capaces de describirla como Tipo I o Tipo II o una mezcla de ambos, entonces podemos usar el siguiente teorema y no tener que encontrar un rectángulo\(R\) que contenga la región.

Teorema: Teorema de Fubini (Forma Fuerte)

Para una función\(f(x,y)\) que es continua en una región\(D\) de Tipo I, tenemos

\[\iint\limits_D f(x,y)\,dA = \iint\limits_D f(x,y)\,dy \space dx = \int_a^b \left[\int_{g_1(x)}^{g_2(x)} f(x,y)\,dy \right] dx. \nonumber \]

Del mismo modo, para una función\(f(x,y)\) que es continua en una región\(D\) de Tipo II, tenemos

\[\iint\limits_D f(x,y)\,dA = \iint\limits_D f(x,y)\,dx \space dy = \int_c^d \left[\int_{h_1(y)}^{h_2(y)} f(x,y)\,dx \right] dy. \nonumber \]

La integral en cada una de estas expresiones es una integral iterada, similar a las que hemos visto antes. Observe que, en la integral interna en la primera expresión, nos integramos\(f(x,y)\) con\(x\) ser sostenidos constantes y los límites de la integración siendo\(g_1(x)\) y\(g_2(x)\). En la integral interna en la segunda expresión, nos integramos\(f(x,y)\) con\(y\) ser sostenidos constantes y los límites de la integración son\(h_1(x)\) y\(h_2(x)\).

Ejemplo\(\PageIndex{2}\): Evaluating an Iterated Integral over a Type I Region

Evaluar la integral\(\displaystyle \iint \limits _D x^2 e^{xy} \,dA\) donde\(D\) se muestra en la Figura\(\PageIndex{5}\).

Solución

Primero construya la región como región Tipo I (Figura\(\PageIndex{5}\)). Aquí\(D = \big\{(x,y) \,|\, 0 \leq x \leq 2, \space \frac{1}{2} x \leq y \leq 1\big\}\). Entonces tenemos

\[\iint \limits _D x^2e^{xy} \,dA = \int_{x=0}^{x=2} \int_{y=1/2x}^{y=1} x^2e^{xy}\,dy\,dx. \nonumber \]

Figura\(\PageIndex{5}\): Podemos expresar región\(D\) como región Tipo I e integrarnos de\(y = \frac{1}{2} x\) a\(y = 1\) entre las líneas\(x = 0\) y\(x = 2\).

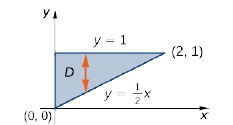
Por lo tanto, tenemos

\[\begin{align*} \int_{x=0}^{x=2}\int_{y=\frac{1}{2}x}^{y=1}x^2e^{xy}\,dy\,dx &= \int_{x=0}^{x=2}\left[\int_{y=\frac{1}{2}x}^{y=1}x^2e^{xy}\,dy\right] dx & &\text{Iterated integral for a Type I region.}\\[5pt] &=\int_{x=0}^{x=2} \left.\left[ x^2 \frac{e^{xy}}{x} \right] \right|_{y=1/2x}^{y=1}\,dx & & \text{Integrate with respect to $y$}\\[5pt] &= \int_{x=0}^{x=2} \left[xe^x - xe^{x^2/2}\right]dx & & \text{Integrate with respect to $x$} \\[5pt] &=\left[xe^x - e^x - e^{\frac{1}{2}x^2} \right] \Big|_{x=0}^{x=2} = 2. \end{align*}\]

En Ejemplo\(\PageIndex{2}\), podríamos haber mirado la región de otra manera, como por ejemplo\(D = \big\{(x,y)\,|\,0 \leq y \leq 1, \space 0 \leq x \leq 2y\big\}\) (Figura\(\PageIndex{6}\)).

Figura\(\PageIndex{6}\).

Esta es una región Tipo II y la integral luciría entonces

\[\iint \limits _D x^2e^{xy}\,dA = \int_{y=0}^{y=1} \int_{x=0}^{x=2y} x^2 e^{xy}\,dx \space dy. \nonumber \]

Sin embargo, si integramos primero con respecto a\(x\) esta integral es largo de computar porque tenemos que usar la integración por partes dos veces.

Ejemplo\(\PageIndex{3}\): Evaluating an Iterated Integral over a Type II Region

Evaluar la integral

\[\iint \limits _D (3x^2 + y^2) \,dA \nonumber \]

donde\(D = \big\{(x,y)\,| \, -2 \leq y \leq 3, \space y^2 - 3 \leq x \leq y + 3\big\}\).

Solución

Observe que\(D\) puede verse como una región Tipo I o Tipo II, como se muestra en la Figura\(\PageIndex{7}\). Sin embargo, en este caso describirlo\(D\) como Tipo I es más complicado que describirlo como Tipo II. Por lo tanto, utilizamos\(D\) como región Tipo II para la integración.

Figura\(\PageIndex{7}\): La región\(D\) en este ejemplo puede ser (a) Tipo I o (b) Tipo II.

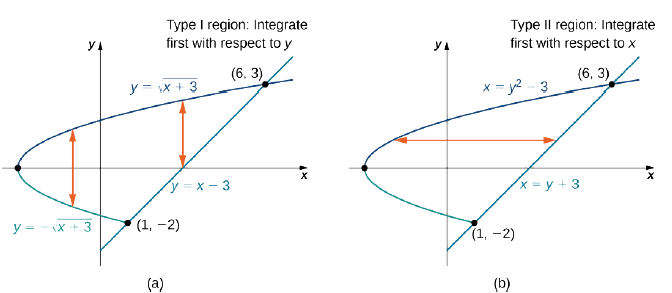
Eligiendo este orden de integración, tenemos

\[\begin{align*} \iint \limits _D (3x^2 + y^2)\,dA &= \int_{y=-2}^{y=3} \int_{x=y^2-3}^{x=y+3} (3x^2 + y^2) \,dx \space dy \\[5pt] &=\int_{y=-2}^{y=3} \left. (x^3 + xy^2) \right|_{y^2-3}^{y+3} \,dy & & \text{Iterated integral, Type II region}\\[5pt] &=\int_{y=-2}^{y=3} \left((y + 3)^3 + (y + 3)y^2 - (y^2 - 3)y^2\right)\,dy \\ &=\int_{-2}^3 (54 + 27y - 12y^2 + 2y^3 + 8y^4 - y^6)\,dy & & \text{Integrate with respect to $x$.} \\[5pt] &= \left[ 54y + \frac{27y^2}{2} - 4y^3 + \frac{y^4}{2} + \frac{8y^5}{5} - \frac{y^7}{7} \right]_{-2}^3 \\ &=\frac{2375}{7}. \end{align*}\]

Ejercicio\(\PageIndex{2}\)

Dibuje la región\(D\) y evalúe la integral iterada\[\iint \limits _D xy \space dy \space dx \nonumber \] donde\(D\) está la región delimitada por las curvas\(y = \cos \space x\) y\(y = \sin \space x\) en el intervalo\([-3\pi/4, \space \pi/4]\).

Pista

Expresar\(D\) como región Tipo I, e integrar con respecto a\(y\) primero.

Contestar

\(\frac{\pi}{4}\)

Recuérdese de Integrales Dobles sobre Regiones Rectangulares las propiedades de integrales dobles. Como hemos visto en los ejemplos aquí, todas estas propiedades también son válidas para una función definida en una región acotada no rectangular en un plano. En particular, la propiedad 3 afirma:

Si\(R = S \cup T\) y\(S \cap T = 0\) excepto en sus límites, entonces

\[\iint \limits _R f(x,y)\,dA = \iint\limits _S f(x,y)\,dA + \iint\limits _T f(x,y) \,dA. \nonumber \]

Del mismo modo, tenemos la siguiente propiedad de integrales dobles sobre una región delimitada no rectangular en un plano.

Teorema: Descomponer regiones en regiones más pequeñas

Supongamos que la región se\(D\) puede expresar como\(D = D_1 \cup D_2\) dónde\(D_1\) y\(D_2\) no se superponen excepto en sus límites. Entonces

\[\iint \limits _D f(x,y) \,dA = \iint \limits _{D_1} f(x,y) \,dA + \iint \limits _{D_2} f(x,y) \,dA. \nonumber \]

Este teorema es particularmente útil para regiones no rectangulares porque permite dividir una región en una unión de regiones de Tipo I y Tipo II. Entonces podemos calcular la doble integral en cada pieza de una manera conveniente, como en el siguiente ejemplo.

Ejemplo\(\PageIndex{4}\): Decomposing Regions

Expresar la región\(D\) mostrada en la Figura\(\PageIndex{8}\) como una unión de regiones de Tipo I o Tipo II, y evaluar la integral

\[\iint \limits _D (2x + 5y)\,dA. \nonumber \]

Figura\(\PageIndex{8}\): Esta región puede descomponerse en una unión de tres regiones de Tipo I o Tipo II.

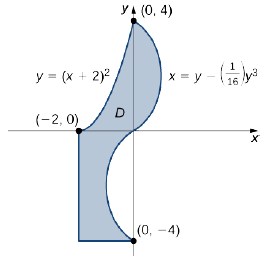
Solución

La región no\(D\) es fácil de descomponer en un solo tipo; en realidad es una combinación de diferentes tipos. Entonces podemos escribirlo como una unión de tres regiones\(D_1\),\(D_2\), y\(D_3\) dónde,\(D_1 = \big\{(x,y)\,| \, -2 \leq x \leq 0, \space 0 \leq y \leq (x + 2)^2 \big\}\),\(D_2 = \big\{(x,y)\,| \, 0 \leq y \leq 4, \space 0 \leq x \leq \big(y - \frac{1}{16} y^3 \big) \big\}\), y\(D_3 = \big\{(x,y)\,| \, -4 \leq y \leq 0, \space -2 \leq x \leq \big(y - \frac{1}{16} y^3 \big) \big\}\). Estas regiones se ilustran más claramente en la Figura\(\PageIndex{9}\).

Figura\(\PageIndex{9}\): La división de la región en tres subregiones facilita la configuración de la integración.

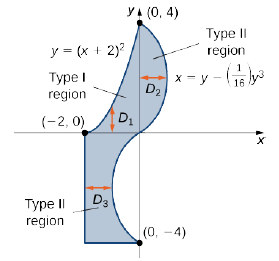
Aquí\(D_1\) está Tipo I y\(D_2\) y\(D_3\) son ambos de Tipo II. Por lo tanto,

\[\begin{align*} \iint\limits_D (2x + 5y)\,dA &= \iint\limits_{D_1} (2x + 5y)\,dA + \iint\limits_{D_2} (2x + 5y)\,dA + \iint\limits_{D_3} (2x + 5y)\,dA \\ &= \int_{x=-2}^{x=0} \int_{y=0}^{y=(x+2)^2} (2x + 5y) \,dy \space dx + \int_{y=0}^{y=4} \int_{x=0}^{x=y-(1/16)y^3} (2 + 5y)\,dx \space dy + \int_{y=-4}^{y=0} \int_{x=-2}^{x=y-(1/16)y^3} (2x + 5y)\,dx \space dy \\ &= \int_{x=-2}^{x=0} \left[\frac{1}{2}(2 + x)^2 (20 + 24x + 5x^2)\right]\,dx + \int_{y=0}^{y=4} \left[\frac{1}{256}y^6 - \frac{7}{16}y^4 + 6y^2 \right]\,dy +\int_{y=-4}^{y=0} \left[\frac{1}{256}y^6 - \frac{7}{16}y^4 + 6y^2 + 10y - 4\right] \,dy\\ &= \frac{40}{3} + \frac{1664}{35} - \frac{1696}{35} = \frac{1304}{105}.\end{align*}\]

Ahora podríamos rehacer este ejemplo usando una unión de dos regiones Tipo II (ver Checkpoint).

Ejercicio\(\PageIndex{3}\)

Considera la región delimitada por las curvas\(y = \ln x\) y\(y = e^x\) en el intervalo\([1,2]\). Descomponer la región en regiones más pequeñas de Tipo II.

Pista

Dibuje la región y divídala en tres regiones para configurarla.

Contestar

\[\big\{(x,y)\,| \, 0 \leq y \leq 1, \space 1 \leq x \leq e^y \big\} \cup \big\{(x,y)\,| \, 1 \leq y \leq e, \space 1 \leq x \leq 2 \big\} \cup \big\{(x,y)\,| \, e \leq y \leq e^2, \space \ln y \leq x \leq 2 \big\} \nonumber \]

Ejercicio\(\PageIndex{4}\)

Ejemplo Rehacer\(\PageIndex{4}\) usando una unión de dos regiones Tipo II.

Pista

\[\big\{(x,y)\,| \, 0 \leq y \leq 4, \space 2 + \sqrt{y} \leq x \leq \big(y - \frac{1}{16}y^3\big) \big\} \cup \big\{(x,y)\,| \, - 4 \leq y \leq 0, \space -2 \leq x \leq \big(y - \frac{1}{16}y^{13}\big) \big\} \nonumber \]

Contestar

Igual que en el ejemplo mostrado.

Cambiando el orden de integración

Como ya hemos visto cuando evaluamos una integral iterada, a veces un orden de integración conduce a un cálculo que es significativamente más simple que el otro orden de integración. A veces el orden de integración no importa, pero es importante aprender a reconocer cuándo un cambio de orden simplificará nuestro trabajo.

Ejemplo\(\PageIndex{5}\): Changing the Order of Integration

Invierta el orden de integración en la integral iterada

\[\int_{x=0}^{x=\sqrt{2}} \int_{y=0}^{y=2-x^2} xe^{x^2} \,dy \space dx. \nonumber \]

Luego evaluar la nueva integral iterada.

Solución

La región tal como se presenta es de Tipo I. Para revertir el orden de integración, primero debemos expresar la región como Tipo II. Consulte la Figura\(\PageIndex{10}\).

Figura\(\PageIndex{10}\): Conversión de una región de Tipo I a Tipo II.

Podemos ver a partir de los límites de integración que la región está delimitada arriba\(y = 2 - x^2\) y abajo por\(y = 0\) donde\(x\) está en el intervalo\([0, \sqrt{2}]\). Al invertir el orden, tenemos la región delimitada a la izquierda por\(x = 0\) y a la derecha por\(x = \sqrt{2 - y}\) donde\(y\) está en el intervalo\([0, 2]\). Lo resolvimos\(y = 2 - x^2\) en cuanto\(x\) a obtener\(x = \sqrt{2 - y}\).

De ahí

\[\begin{align*} \int_0^{\sqrt{2}} \int_0^{2-x^2} xe^{x^2} dy \space dx &= \int_0^2 \int_0^{\sqrt{2-y}} xe^{x^2}\,dx \space dy &\text{Reverse the order of integration then use substitution.} \\[4pt] &= \int_0^2 \left[\left.\frac{1}{2}e^{x^2}\right|_0^{\sqrt{2-y}}\right] dy = \int_0^2\frac{1}{2}(e^{2-y} - 1)\,dy \\[4pt] &= -\left.\frac{1}{2}(e^{2-y} + y)\right|_0^2 = \frac{1}{2}(e^2 - 3). \end{align*}\]

Ejemplo\(\PageIndex{6}\): Evaluating an Iterated Integral by Reversing the Order of Integration

Considere la integral iterada

\[\iint\limits_R f(x,y)\,dx \space dy \nonumber \]

donde\(z = f(x,y) = x - 2y\) sobre una región triangular\(R\) que tiene lados en\(x = 0, \space y = 0\), y la línea\(x + y = 1\). Dibuje la región y luego evalúe la integral iterada mediante

1. integrando primero con respecto a\(y\) y luego
2. integrando primero con respecto a\(x\).

Solución

Un boceto de la región aparece en la Figura\(\PageIndex{11}\).

Figura\(\PageIndex{11}\): Una región triangular\(R\) para integrar de dos maneras.

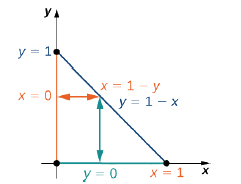
Podemos completar esta integración de dos maneras diferentes.

a. Una forma de verlo es integrando primero\(y\) de\(y = 0\) a\(y = 1 - x\) verticalmente y luego integrando\(x\) de\(x = 0\) a\(x = 1\):

\[\begin{align*} \iint\limits_R f(x,y) \,dx \space dy &= \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} (x - 2y) \,dy \space dx = \int_{x=0}^{x=1}\left(xy - 2y^2\right)\Big|_{y=0}^{y=1-x} dx \\[4pt] &=\int_{x=0}^{x=1} \left[ x(1 - x) - (1 - x)^2\right] \,dx = \int_{x=0}^{x=1} [ -1 + 3x - 2x^2] dx = \left[ -x + \frac{3}{2}x^2 - \frac{2}{3} x^3 \right]\Big|_{x=0}^{x=1} = -\frac{1}{6}. \end{align*}\]

b. La otra forma de hacer este problema es integrando primero\(x\) de\(x = 0\) a\(x = 1 - y\) horizontalmente y luego integrando\(y\) de\(y = 0\) a\(y = 1\):

\[\begin{align*} \iint \limits _D (3x^2 + y^2)\,dA &= \int_{y=-2}^{y=3} \int_{x=y^2-3}^{x=y+3} (3x^2 + y^2) \,dx \space dy \\[4pt] &=\int_{y=-2}^{y=3} (x^3 + xy^2) \Big|_{y^2-3}^{y+3} \,dy & & \text{Iterated integral, Type II region}\\[4pt] &=\int_{y=-2}^{y=3} \left((y + 3)^3 + (y + 3)y^2 - (y^2 - 3)y^2\right)\,dy \\[4pt] &=\int_{-2}^3 (54 + 27y - 12y^2 + 2y^3 + 8y^4 - y^6)\,dy & & \text{Integrate with respect to $x$.} \\[4pt] &= \left( 54y + \frac{27y^2}{2} - 4y^3 + \frac{y^4}{2} + \frac{8y^5}{5} - \frac{y^7}{7} \right)\Big|_{-2}^3 \\[4pt] &=\frac{2375}{7}. \end{align*}\]

Ejercicio\(\PageIndex{5}\)

Evaluar la integral iterada\(\displaystyle \iint\limits_D (x^2 + y^2)\,dA\) sobre la región\(D\) en el primer cuadrante entre las funciones\(y = 2x\) y\(y = x^2\). Evaluar la integral iterada integrando primero con respecto a\(y\) y luego integrando primero con resect to\(x\).

Pista

Esboza la región y sigue Ejemplo\(\PageIndex{6}\).

Contestar

\(\frac{216}{35}\)

Cálculo de volúmenes, áreas y valores promedio

Podemos usar integrales dobles sobre regiones generales para calcular volúmenes, áreas y valores promedio. Los métodos son los mismos que los de Integrales Dobles sobre Regiones Rectangulares, pero sin la restricción a una región rectangular, ahora podemos resolver una mayor variedad de problemas.

Ejemplo\(\PageIndex{7}\): Finding the Volume of a Tetrahedron

Encuentra el volumen del sólido delimitado por los planos\(x = 0, \space y = 0, \space z = 0\), y\(2x + 3y + z = 6\).

Solución

El sólido es un tetraedro con la base en el\(xy\) plano y una altura\(z = 6 - 2x - 3y\). La base es la región\(D\) delimitada por las líneas,\(x = 0\),\(y = 0\) y\(2x + 3y = 6\) donde\(z = 0\) (Figura\(\PageIndex{12}\)). Tenga en cuenta que podemos considerar la región\(D\) como Tipo I o como Tipo II, y podemos integrarla en ambas formas.

Figura\(\PageIndex{12}\): Un tetraedro que consta de los tres planos de coordenadas y el plano\(z = 6 - 2x - 3y\), con la base unida por\(x = 0, \space y = 0\), y\(2x + 3y = 6\).

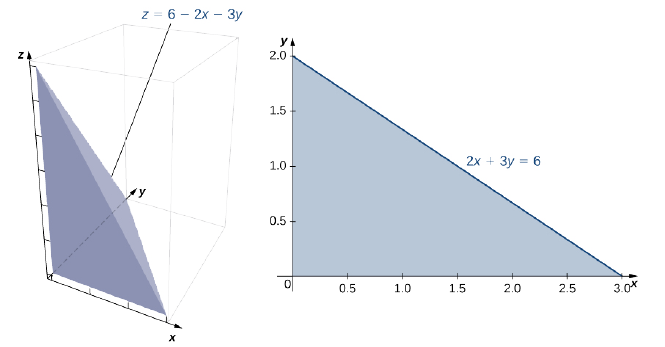
Primero, considerar\(D\) como una región Tipo I, y por ende\(D = \big\{(x,y)\,| \, 0 \leq x \leq 3, \space 0 \leq y \leq 2 - \frac{2}{3} x \big\}\).

Por lo tanto, el volumen es

\[\begin{align*} V &= \int_{x=0}^{x=3} \int_{y=0}^{y=2-(2x/3)} (6 - 2x - 3y) \,dy \space dx = \int_{x=0}^{x=3} \left[ \left.\left( 6y - 2xy - \frac{3}{2}y^2\right)\right|_{y=0}^{y=2-(2x/3)} \right] \,dx\\[4pt] &= \int_{x=0}^{x=3} \left[\frac{2}{3} (x - 3)^2 \right] \,dx = 6. \end{align*}\]

Ahora consideremos\(D\) como una región Tipo II, así\(D = \big\{(x,y)\,| \, 0 \leq y \leq 2, \space 0 \leq x \leq 3 - \frac{3}{2}y \big\}\). En este cálculo, el volumen es

\[\begin{align*} V &= \int_{y=0}^{y=2} \int_{x=0}^{x=3-(3y/2)} (6 - 2x - 3y)\,dx \space dy = \int_{y=0}^{y=2} \left[(6x - x^2 - 3xy)\Big|_{x=0}^{x=3-(3y/2)} \right] \,dy \\[4pt] &= \int_{y=0}^{y=2} \left[\frac{9}{4}(y - 2)^2 \right] \,dy = 6.\end{align*}\]

Por lo tanto, el volumen es de 6 unidades cúbicas.

Ejercicio\(\PageIndex{6}\)

Encuentra el volumen del sólido delimitado arriba por\(f(x,y) = 10 - 2x + y\) sobre la región encerrada por las curvas\(y = 0\) y\(y = e^x\) dónde\(x\) está en el intervalo\([0,1]\).

Pista

Esbozar la región y describirla como Tipo I.

Contestar

\(\frac{e^2}{4} + 10e - \frac{49}{4}\)unidades cúbicas

Encontrar el área de una región rectangular es fácil, pero encontrar el área de una región no rectangular no es tan fácil. Como hemos visto, podemos usar integrales dobles para encontrar un área rectangular. De hecho, esto resulta muy útil para encontrar el área de una región general no rectangular, como se indica en la siguiente definición.

Definición: Integrales dobles

El área de una región delimitada por plano\(D\) se define como la doble integral

\[\iint\limits_D 1\,dA. \nonumber \]

Ya hemos visto cómo encontrar áreas en términos de integración única. Aquí estamos viendo otra forma de encontrar áreas mediante el uso de dobles integrales, lo cual puede ser muy útil, como veremos en las secciones posteriores de este capítulo.

Ejemplo\(\PageIndex{8}\): Finding the Area of a Region

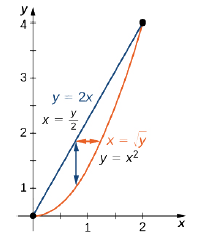
Encuentra el área de la región delimitada por debajo por la curva\(y = x^2\) y arriba por la línea\(y = 2x\) en el primer cuadrante (Figura\(\PageIndex{13}\)).

Figura\(\PageIndex{13}\): La región delimitada por\(y = x^2\) y\(y = 2x\).

Solución

Solo tenemos que integrar la función constante\(f(x,y) = 1\) sobre la región. Así, el área\(A\) de la región delimitada es\(\displaystyle \int_{x=0}^{x=2} \int_{y=x^2}^{y=2x} dy \space dx \space \text{or} \space \int_{y=0}^{y=4} \int_{x=y/2}^{x=\sqrt{y}} dx \space dy:\)

\[\begin{align*} A &= \iint\limits_D 1\,dx \space dy \\[4pt] &= \int_{x=0}^{x=2} \int_{y=x^2}^{y=2x} 1\,dy \space dx \\[4pt] &= \int_{x=0}^{x=2} \left(y\Big|_{y=x^2}^{y=2x} \right) \,dx \\[4pt] &= \int_{x=0}^{x=2} (2x - x^2)\,dx \\[4pt] &= \left(x^2 - \frac{x^3}{3}\right) \Big|_0^2 = \frac{4}{3}. \end{align*}\]

Ejercicio\(\PageIndex{7}\)

Encuentra el área de una región delimitada arriba por la curva\(y = x^3\) y abajo por\(y = 0\) sobre el intervalo\([0,3]\).

Pista

Esbozar la región.

Contestar

\(\frac{81}{4}\)unidades cuadradas

También podemos usar una doble integral para encontrar el valor promedio de una función sobre una región general. La definición es una extensión directa de la fórmula anterior.

Definición: El valor promedio de una función

Si\(f (x,y)\) es integrable sobre una región delimitada por plano\(D\) con área positiva\(A(D)\), entonces el valor promedio de la función es

\[f_{ave} = \frac{1}{A(D)} \iint\limits_D f(x,y) \,dA. \nonumber \]

Tenga en cuenta que el área es\(\displaystyle A(D) = \iint\limits_D 1\,dA\).

Ejemplo\(\PageIndex{9}\): Finding an Average Value

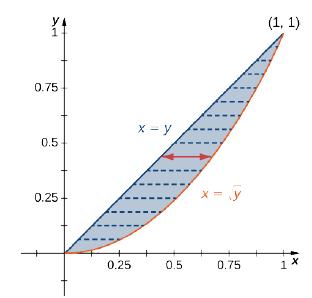
Encuentra el valor promedio de la función\(f(x,y) = 7xy^2\) en la región delimitada por la línea\(x = y\) y la curva\(x = \sqrt{y}\) (Figura\(\PageIndex{14}\)).

Figura\(\PageIndex{14}\): La región delimitada por\(x = y\) y\(x = \sqrt{y}\).

Solución

Primero encuentra la zona\(A(D)\) donde la región\(D\) está dada por la figura. Tenemos

\[A(D) = \iint\limits_D 1\,dA = \int_{y=0}^{y=1} \int_{x=y}^{x=\sqrt{y}} 1\,dx \space dy = \int_{y=0}^{y=1} \left[x \Big|_{x=y}^{x=\sqrt{y}} \right] \,dy = \int_{y=0}^{y=1} (\sqrt{y} - y) \,dy = \frac{2}{3}\left. y^{2/3} - \frac{y^2}{2} \right|_0^1 = \frac{1}{6} \nonumber \]

Entonces el valor promedio de la función dada sobre esta región es

\[\begin{align*} f_{ave} = \frac{1}{A(D)} \iint\limits_D f(x,y) \,dA = \frac{1}{A(D)} \int_{y=0}^{y=1}\int_{x=y}^{x=\sqrt{y}} 7xy^2 \,dx \space dy = \frac{1}{1/6} \int_{y=0}^{y=1} \left[ \left. \frac{7}{2} x^2y^2 \right|_{x=y}^{x=\sqrt{y}} \right] \,dy \\ = 6 \int_{y=0}^{y=1} \left[ \frac{7}{2} y^2 (y - y^2)\right] \,dy = 6\int_{y=0}^{y=1} \left[ \frac{7}{2} (y^3 -y^4) \right] \,dy = \frac{42}{2} \left. \left( \frac{y^4}{4} - \frac{y^5}{5}\right) \right|_0^1 = \frac{42}{40} = \frac{21}{20}. \end{align*}\]

Ejercicio\(\PageIndex{8}\)

Encuentra el valor promedio de la función\(f(x,y) = xy\) sobre el triángulo con vértices\((0,0), \space (1,0)\) y\((1,3)\).

Pista

Expresar la línea de unión\((0,0)\) y\((1,3)\) como una función\(y = g(x)\).

Contestar

\(\frac{3}{4}\)

Integrales dobles inadecuados

Una doble integral inadecuada es una integral\(\displaystyle \iint\limits_D f \,dA\) donde o bien\(D\) es una región no delimitada o\(f\) es una función no delimitada. Por ejemplo,\(D = \big\{(x,y) \,|\,|x - y| \geq 2\big\}\) es una región no delimitada, y la función\(f(x,y) = 1/(1 - x^2 - 2y^2)\) sobre la elipse\(x^2 + 3y^2 \geq 1\) es una función no delimitada. Por lo tanto, las dos integrales siguientes son integrales inadecuadas:

1. \[\iint\limits_D xy \space dA \space \text{where} \space D = \big\{(x,y)| | \, x - y| \geq 2 \big\}; \nonumber \]
2. \[\iint\limits_D \frac{1}{1 - x^2 -2y^2}\,dA \space \text{where} \space D = \big\{(x,y)| \, x^2 + 3y^2 \leq 1 \big\}. \nonumber \]

En esta sección nos gustaría tratar integrales inadecuadas de funciones sobre rectángulos o regiones simples de tal manera que f tiene solo finitamente muchas discontinuidades. No todas esas integrales inadecuadas pueden ser evaluadas; sin embargo, una forma del teorema de Fubini sí se aplica para algunos tipos de integrales inadecuadas.

Teorema: Teorema de Fubini para Integrales Inadecuadas

Si\(D\) es un rectángulo delimitado o una región simple en el plano definido por

\(\big\{(x,y)\,: a \leq x \leq b, \space g(x) \leq y \leq h(x) \big\}\)y también por

\(\big\{(x,y)\,: c \leq y \leq d, \space j(y) \leq x \leq k(y)\big\}\)y\(f\) es una función no negativa\(D\) con finitamente muchas discontinuidades en el interior de\(D\) entonces

\[\iint\limits_D f \space dA = \int_{x=a}^{x=b} \int_{y=g(x)}^{y=h(x)} f(x,y) \,dy \space dx = \int_{y=c}^{y=d} \int_{x=j(y)}^{x=k(y)} f(x,y) \,dx \space dy \nonumber \]

Es muy importante señalar que requerimos que la función no sea negativa\(D\) para que funcione el teorema. Consideramos solo el caso donde la función tiene finitamente muchas discontinuidades en su interior\(D\).

Ejemplo\(\PageIndex{10}\): Evaluating a Double Improper Integral

Considerar la función\(f(x,y) = \frac{e^y}{y}\) sobre la región\(D = \big\{(x,y)\,: 0 \leq x \leq 1, \space x \leq y \leq \sqrt{x}\big\}.\)

Observe que la función es no negativa y continua en todos los puntos\(D\) excepto\((0,0)\). Utilizar el teorema de Fubini para evaluar la integral impropia.

Solución

Primero trazamos la región\(D\) (Figura\(\PageIndex{15}\)); luego la expresamos de otra manera.

Figura\(\PageIndex{15}\): La función\(f\) es continua en todos los puntos de la región\(D\) excepto\((0,0)\).

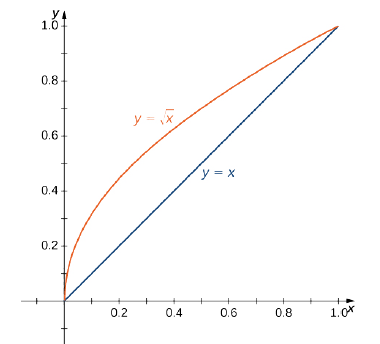
La otra forma de expresar la misma región\(D\) es

\[D = \big\{(x,y)\,: \, 0 \leq y \leq 1, \space y^2 \leq x \leq y \big\}. \nonumber \]

Así podemos usar el teorema de Fubini para integrales impropias y evaluar la integral como

\[\int_{y=0}^{y=1} \int_{x=y^2}^{x=y} \frac{e^y}{y} \,dx \space dy. \nonumber \]

Por lo tanto, tenemos

\[\int_{y=0}^{y=1} \int_{x=y^2}^{x=y} \frac{e^y}{y} \,dx \space dy = \int_{y=0}^{y=1} \left. \frac{e^y}{y}x\right|_{x=y^2}^{x=y} \,dy = \int_{y=0}^{y=1} \frac{e^y}{y} (y - y^2) \,dy = \int_0^1 (e^y - ye^y)\,dy = e - 2. \nonumber \]

Como se mencionó anteriormente, también tenemos una integral inadecuada si la región de integración no tiene límites. Supongamos ahora que la función\(f\) es continua en un rectángulo no acotado\(R\).

Teorema: Integrales inadecuadas en una región no delimitada

Si\(R\) es un rectángulo sin límites como\(R = \big\{(x,y)\,: \, a \leq x \leq \infty, \space c \leq y \leq \infty \big\}\), entonces cuando existe el límite, tenemos

\[\iint\limits_R f(x,y) \,dA = \lim_{(b,d) \rightarrow (\infty, \infty)} \int_a^b \left(\int_c^d f (x,y) \,dy \right) dx = \lim_{(b,d) \rightarrow (\infty, \infty)} \int_c^d \left(\int_a^b f(x,y) \,dx \right) dy. \nonumber \]

El siguiente ejemplo muestra cómo este teorema puede ser utilizado en ciertos casos de integrales impropias.

Ejemplo\(\PageIndex{11}\)

Evaluar la integral\(\iint\limits_R xye^{-x^2-y^2}\,dA\) donde\(R\) se encuentra el primer cuadrante del plano.

Solución

La región\(R\) es el primer cuadrante del plano, el cual no tiene límites. Entonces

\[\begin{align*} \iint\limits_R xye^{-x^2-y^2} \,dA &= \lim_{(b,d) \rightarrow (\infty, \infty)} \int_{x=0}^{x=b} \left(\int_{y=0}^{y=d} xye^{-x^2-y^2} dy\right) \,dx \\ &= \lim_{(b,d) \rightarrow (\infty, \infty)} \int_{y=0}^{x=b} xye^{-x^2-y^2} \,dy \\ &= \lim_{(b,d) \rightarrow (\infty, \infty)} \frac{1}{4} \left(1 - e^{-b^2}\right) \left( 1 - e^{-d^2}\right) = \frac{1}{4} \end{align*}\]

Por lo tanto,

\[\iint\limits_R xye^{-x^2-y^2}\,dA \nonumber \]

es convergente y el valor es\(\frac{1}{4}\).

Ejercicio\(\PageIndex{9}\)

\[\iint\limits_D \frac{y}{\sqrt{1 - x^2 - y^2}}dA \nonumber \]donde\(D = \big\{(x,y)\,: \, x \geq 0, \space y \geq 0, \space x^2 + y^2 \leq 1 \big\}\).

Pista

Observe que la integral es no negativa y discontinua en\(x^2 + y^2 = 1\). Expresar la región\(D\) como\(D = \big\{(x,y)\,: \, 0 \leq x \leq 1, \space 0 \leq y \leq \sqrt{1 - x^2} \big\}\) e integrar utilizando el método de sustitución.

Contestar

\(\frac{\pi}{4}\)

En algunas situaciones en la teoría de la probabilidad, podemos obtener una idea de un problema cuando somos capaces de usar integrales dobles sobre regiones generales. Antes de repasar un ejemplo con una doble integral, necesitamos establecer algunas definiciones y familiarizarnos con algunas propiedades importantes.

Definición: Función de Densidad de Articulación

Considera un par de variables aleatorias continuas\(X\) y\(Y\) como los cumpleaños de dos personas o el número de días soleados y lluviosos en un mes. La función\(f\) de densidad conjunta de\(X\) y\(Y\) satisface la probabilidad que\((X,Y)\) se encuentra en una región determinada\(D\):

\[P((X,Y) \in D) = \iint\limits_D f(x,y) \,dA. \nonumber \]

Dado que las probabilidades nunca pueden ser negativas y deben estar entre 0 y 1, la función de densidad conjunta satisface la siguiente desigualdad y ecuación:

\[f(x,y) \geq 0 \space \text{and} \space \iint\limits_R f(x,y) \,dA = 1. \nonumber \]

Definición: Variables Aleatorias Independientes

Las variables\(X\) y\(Y\) se dice que son variables aleatorias independientes si su función de densidad conjunta es el producto de sus funciones de densidad individuales:

\[f(x,y) = f_1(x) f_2(y). \nonumber \]

Ejemplo\(\PageIndex{12}\): Application to Probability

En el restaurante Sydney's, los clientes deben esperar un promedio de 15 minutos por una mesa. Desde el momento en que están sentados hasta que hayan terminado su comida se requieren 40 minutos adicionales, en promedio. ¿Cuál es la probabilidad de que un cliente pase menos de hora y media en el restaurante, asumiendo que esperar una mesa y completar la comida son eventos independientes?

Solución

Los tiempos de espera son modelados matemáticamente por funciones de densidad exponencial,\(m\) siendo el tiempo de espera promedio, como

\[f(t) = \begin{cases} 0, & \text{if}\; t<0 \\ \dfrac{1}{m}e^{-t/m}, & \text{if} \; t\geq 0.\end{cases} \nonumber \]

si\(X\) y\(Y\) son variables aleatorias para 'esperar una mesa' y 'completar la comida', entonces las funciones de densidad de probabilidad son, respectivamente,

\[f_1(x) = \begin{cases} 0, & \text{if}\; x<0. \\ \dfrac{1}{15} e^{-x/15}, & \text{if} \; x\geq 0. \end{cases} \quad \text{and} \quad f_2(y) = \begin{cases} 0, & \text{if}\; y<0 \\ \dfrac{1}{40} e^{-y/40}, & \text{if}\; y\geq 0. \end{cases} \nonumber \]

Claramente, los eventos son independientes y por lo tanto la función de densidad conjunta es el producto de las funciones individuales

\[f(x,y) = f_1(x)f_2(y) = \begin{cases} 0, & \text{if} \; x<0 \; \text{or} \; y<0, \\ \dfrac{1}{600} e^{-x/15}, & \text{if} \; x,y\geq 0 \end{cases} \nonumber \]

Queremos encontrar la probabilidad de que el tiempo combinado\(X + Y\) sea inferior a 90 minutos. En términos de geometría, significa que la región\(D\) está en el primer cuadrante delimitada por la línea\(x + y = 90\) (Figura\(\PageIndex{16}\)).

Figura\(\PageIndex{16}\): La región de integración para una función conjunta de densidad de probabilidad.

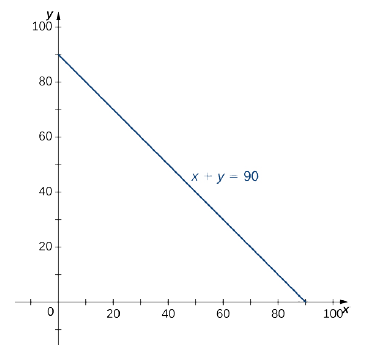
De ahí que la probabilidad que\((X,Y)\) se encuentre en la región\(D\) es

\[P(X + Y \leq 90) = P((X,Y) \in D) = \iint\limits_D f(x,y) \,dA = \iint\limits_D \frac{1}{600}e^{-x/15} e^{-y/40} \,dA. \nonumber \]

Ya que\(x + y = 90\) es lo mismo que\(y = 90 - x\), tenemos una región de Tipo I, entonces

\[\begin{align*} D &= \big\{(x,y)\,|\,0 \leq x \leq 90, \space 0 \leq y \leq 90 - x\big\}, \\[6pt] P(X + Y \leq 90) &= \frac{1}{600} \int_{x=0}^{x=90} \int_{y=0}^{y=90-x} e^{-(/15}e^{-y/40}dx \space dy = \frac{1}{600} \int_{x=0}^{x=90} \int_{y=0}^{y=90-x}e^{-x/15}e^{-y/40} dx \space dy \\[6pt] &= \frac{1}{600} \int_{x=0}^{x=90} \int_{y=0}^{y=90-x} e^{-(x/15+y/40)}dx \space dy = 0.8328 \end{align*}\]

Así, existe la\(83.2\%\) posibilidad de que un cliente pase menos de hora y media en el restaurante.

Otra aplicación importante en la probabilidad que puede implicar dobles integrales inadecuadas es el cálculo de los valores esperados. Primero definimos este concepto y luego mostramos un ejemplo de un cálculo.

Definición: Valores esperados

En teoría de probabilidad, denotamos los valores esperados\(E(X)\) y\(E(Y)\) respectivamente, como los resultados más probables de los eventos. Los valores esperados\(E(X)\) y\(E(Y)\) están dados por

\[E(X) = \iint\limits_S x\,f(x,y) \,dA \space and \space E(Y) = \iint\limits_S y\,f (x,y) \,dA, \nonumber \]

donde\(S\) está el espacio muestral de las variables aleatorias\(X\) y\(Y\).

Ejemplo\(\PageIndex{13}\): Finding Expected Value

Encuentra el tiempo esperado para los eventos 'esperando una mesa' y 'completar la comida' en Ejemplo\(\PageIndex{12}\).

Solución

Usando el primer cuadrante del plano de coordenadas rectangulares como espacio muestral, tenemos integrales inadecuadas para\(E(X)\) y\(E(Y)\). El tiempo esperado para una mesa es

\ [\ begin {alinear*} E (X) &=\ iint\ límits_s x\ frac {1} {600} e^ {-x/15} e^ {-y/40}\, dA\\ [6pt]
&=\ frac {1} {600}\ int_ {x=0} ^ {x=\ infty}\ int_ {y=0} ^ {y=\ infty} xe^ {-x/15} e^ {-y/40} dA\\ [6pt]
&=\ frac {1} {600}\ lim_ {(a, b)\ fila derecha (\ infty,\ infty)}\ int_ {x=0} ^ {x=a}\ int_ {y=0} ^ {y=b} xe^ {-x/15} e^ {-y/40} dx\ espacio dy\\ [6pt]
&=\ frac {1} {600}\ izquierda (\ lim_ {a\ fila derecha\ infty}\ int_ {x=0} ^ {x=a} xe^ {-x/15} dx\ derecha)\ izquierda (\ lim_ {b\ fila derecha\ infty}\ int_ {y=0} ^ {y=b} e^ {-y/40} dy\ derecha)\\ [6pt]
&=\ frac {1} {600}\ izquierda (\ izquierda. (\ lim_ {a\ fila derecha\ infty} (-15e^ {-x/15} (x + 15)))\ derecha|_ {x=0} ^ {x=a}\ derecha)\ izquierda (\ izquierda. (\ lim_ {b\ fila derecha\ infty} (-40e^ {-y/40}))\ derecha|_ {y=0} ^ {y=b}\ derecha)\\ [6pt]
&=\ frac {1} {600}\ izquierda (\ lim_ {a\ fila derecha\ infty} (-15e^ {-a/15} (x + 15) + 225)\ derecha)\ izquierda (\ lim_ {b\ fila derecha\ infty} (- 40e^ {-b/40} + 40)\ derecha)\\ [6pt]
&=\ frac {1} {600} (225) (40) = 15. \ end {alinear*}\]

Un cálculo similar lo demuestra\(E(Y) = 40\). Esto significa que los valores esperados de los dos eventos aleatorios son el tiempo de espera promedio y el tiempo promedio de comedor, respectivamente.

Ejercicio\(\PageIndex{10}\)

La función de densidad conjunta para dos variables aleatorias\(X\) y\(Y\) viene dada por

\[f(x,y) =\begin{cases}\frac{1}{600} (x^2 + y^2),\; & \text{if} \; \leq x \leq 15, \; 0 \leq y \leq 10 \\ 0, & \text{otherwise} \end{cases} \nonumber \]

Encuentra la probabilidad que\(X\) es como máximo 10 y\(Y\) es al menos 5.

Pista

Compute la probabilidad

\[P(X \leq 10, \space Y \geq 5) = \int_{x=-\infty}^{10} \int_{y=5}^{y=10} \frac{1}{6000} (x^2 + y^2) dy \space dx. \nonumber \]

Contestar

\(\frac{55}{72} \approx 0.7638\)

Conceptos clave

• Una región delimitada general\(D\) en el plano es una región que se puede encerrar dentro de una región rectangular. Podemos usar esta idea para definir una doble integral sobre una región delimitada general.
• Para evaluar una integral iterada de una función sobre una región general no rectangular, se esboza la región y la expresamos como una región de Tipo I o como una región de Tipo II o como una unión de varias regiones de Tipo I o Tipo II que se superponen solo en sus límites.
• Podemos usar integrales dobles para encontrar volúmenes, áreas y valores promedio de una función sobre regiones generales, de manera similar a los cálculos sobre regiones rectangulares.
• Podemos usar el teorema de Fubini para integrales inadecuadas para evaluar algunos tipos de integrales inadecuadas.

Ecuaciones Clave

• Integral iterada sobre una región Tipo I

\[\iint\limits_D f(x,y) \,dA = \iint\limits_D f(x,y) \,dy \space dx = \int_a^b \left[\int_{g_1(x)}^{g_2(x)} f(x,y) \,dy \right] dx \nonumber \]

• Integral iterada sobre una región Tipo II

\[\iint\limits_D f(x,y) \,dA = \iint\limits_D (x,y) \,dx \space dy = \int_c^d \left[ \int_{h_1(y)}^{h_2(y)} f(x,y) \,dx \right] dy \nonumber \]

Glosario

doble integral impropia

una integral doble sobre una región no delimitada o de una función no delimitada

Tipo I

una región\(D\) en el plano\(xy\) - es Tipo I si se encuentra entre dos líneas verticales y las gráficas de dos funciones continuas\(g_1(x)\) y\(g_2(x)\)

Tipo II

una región\(D\) en el\(xy\) plano -es Tipo II si se encuentra entre dos líneas horizontales y las gráficas de dos funciones continuas\(h_1(y)\) y\(h_2(h)\)